9.2.1总体取值规律的估计 同步检测(含解析)
文档属性
| 名称 | 9.2.1总体取值规律的估计 同步检测(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 554.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-26 00:00:00 | ||
图片预览




文档简介
9.2.1 总体取值规律的估计(同步检测)
一、选择题
1.对“小康县”的经济评价标准如下:①年人均收入不小于7 000元;
②年人均食品支出不大于收入的35%. 某县有40万人,调查数据如下:
年人均收入/元 0 2 000 4 000 6 000 8 000 10 000 12 000 16 000
人数/万人 6 3 5 5 6 7 5 3
则该县( )
A.是小康县 B.达到标准①,未达到标准②,不是小康县
C.两个标准都未达到,不是小康县 D.达到标准②,未达到标准①,不是小康县
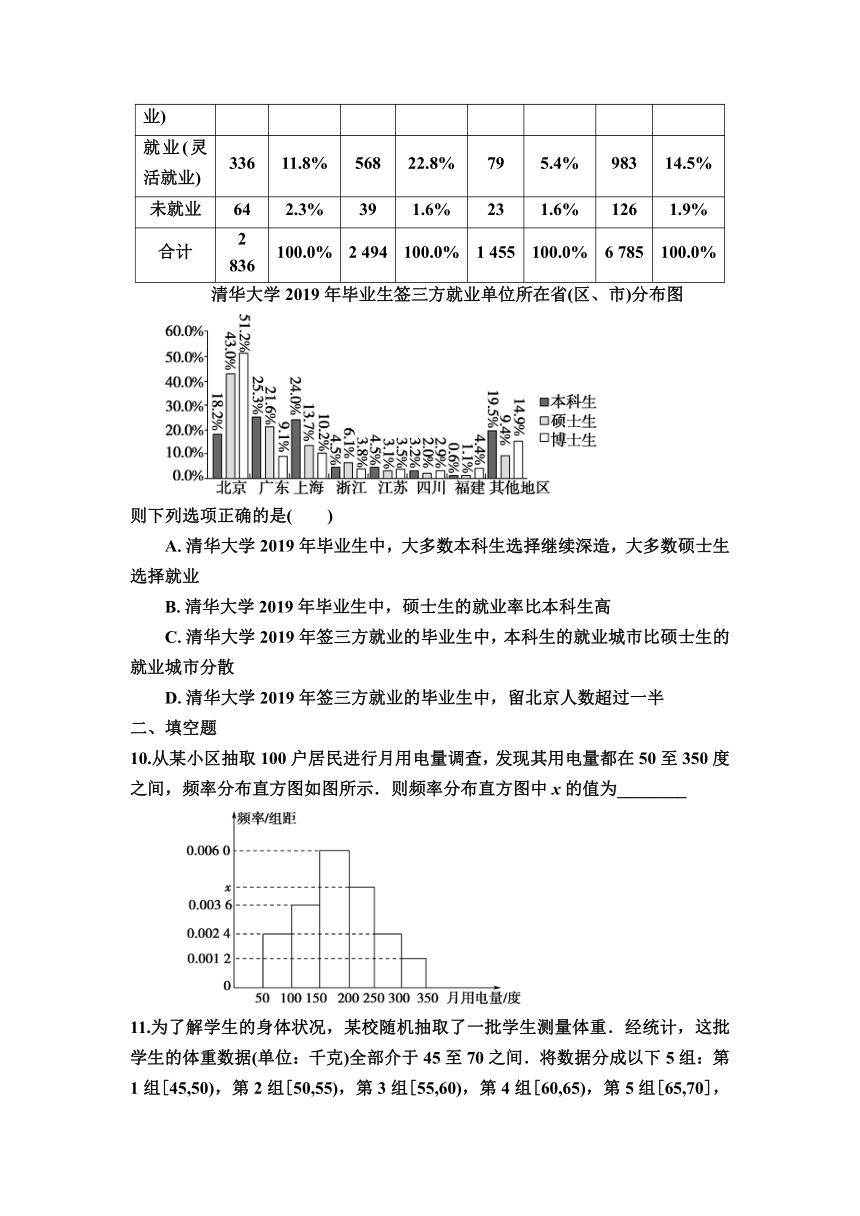
2.从一批零件中抽取80个,测量其直径(单位:mm),将所得数据分为9组:[5.31,5.33),[5.33,5.35),…,[5.45,5.47),[5.47,5.49],并整理得到如图所示的频率分布直方图,则在被抽取的零件中,直径落在区间[5.43,5.47)内的个数为( )
A.10 B.18 C.20 D.36
3.比较甲、乙两名学生的数学学科素养的各项能力指标值(满分为5分,分值高者为优),绘制了如图所示的六维能力雷达图,例如图中甲的数学抽象能力指标值为4,乙的数学抽象能力指标值为5,则下面叙述正确的是( )
A.乙的逻辑推理能力指标值优于甲的逻辑推理能力指标值
B.甲的数学建模能力指标值优于乙的直观想象能力指标值
C.乙的六维能力指标值整体水平优于甲的六维能力指标值整体水平
D.甲的数学运算能力指标值优于甲的直观想象能力指标值
4.某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].根据直方图,这200名学生中每周的自习时间不少于22.5小时的人数是( )
A.56 B.60 C.120 D.140
5.随着2022年北京冬奥会临近,中国冰雪产业快速发展,冰雪运动人数快速上升,冰雪运动市场需求得到释放,将引领户外用品行业市场增长.如图是2012年至2018年中国雪场滑雪人次(单位:万)与同比增长率的统计图,则下列结论中不正确的是( )
A.2013年至2018年,中国雪场滑雪人次逐年增加
B.2013年至2015年,中国雪场滑雪人次和同比增长率均逐年增加
C.2018年与2013年相比,中国雪场滑雪人次的同比增长率近似相等,所以同比增长人数也近似相等
D.2018年与2016年相比,中国雪场滑雪人次增长率约为30.5%
6.一个容量为32的样本中,已知某组样本的频率为0.125,则该组样本的频数为( )
A.2 B.4 C.6 D.8
7.学校为了调查学生在课外读物方面的支出情况,抽取了一个容量为n的样本,其频率分布直方图如图所示,其中支出(单位:元)在[50,60]内的学生有30人,则n的值为( )
A.100 B.1 000 C.90 D.900
8.某公司2019年在各个项目中总投资500万元,如图是几类项目的投资占比情况,已知在1万元以上的项目投资中,少于3万元的项目投资占,那么不少于3万元的项目投资共有( )
A.56万元 B.65万元 C.91万元 D.147万元
9.(多选)如下统计表和如图所示的分布图取自《清华大学2019年毕业生就业质量报告》.
清华大学2019年毕业生去向分布情况统计表
毕业去向 本科生 硕士生 博士生 总体
人数 比例 人数 比例 人数 比例 人数 比例
深造(国内) 1 583 55.8% 94 3.8% 290 19.9% 1 967 29.0%
深造(出国) 699 24.6% 137 5.5% 199 13.7% 1 035 15.3%
就业(签三方就业) 154 5.4% 1 656 66.4% 864 59.4% 2 674 39.4%
就业(灵活就业) 336 11.8% 568 22.8% 79 5.4% 983 14.5%
未就业 64 2.3% 39 1.6% 23 1.6% 126 1.9%
合计 2 836 100.0% 2 494 100.0% 1 455 100.0% 6 785 100.0%
清华大学2019年毕业生签三方就业单位所在省(区、市)分布图
则下列选项正确的是( )
A.清华大学2019年毕业生中,大多数本科生选择继续深造,大多数硕士生选择就业
B.清华大学2019年毕业生中,硕士生的就业率比本科生高
C.清华大学2019年签三方就业的毕业生中,本科生的就业城市比硕士生的就业城市分散
D.清华大学2019年签三方就业的毕业生中,留北京人数超过一半
二、填空题
10.从某小区抽取100户居民进行月用电量调查,发现其用电量都在50至350度之间,频率分布直方图如图所示.则频率分布直方图中x的值为________
11.为了解学生的身体状况,某校随机抽取了一批学生测量体重.经统计,这批学生的体重数据(单位:千克)全部介于45至70之间.将数据分成以下5组:第1组[45,50),第2组[50,55),第3组[55,60),第4组[60,65),第5组[65,70],得到如图所示的频率分布直方图,则a=________.现采用分层随机抽样的方法,从第3,4,5组中随机抽取6名学生,则第3,4,5组抽取的学生人数依次为________
12.一个容量为100的样本,其数据的分组与各组的频数如下表:
组别 [0,10) [10,20) [20,30) [30,40) [40,50) [50,60) [60,70]
频数 12 13 24 15 16 13 7
则样本数据落在[10,40)上的频率为________
13.一个样本的容量为72,分成5组,已知第一、五组的频数都为8,第二、四组的频率都为,则第三组的频数为________
三、解答题
14.2020年,面对突如其来的新冠肺炎疫情中,在党中央领导下,各地区各部门统筹疫情防控和经济社会发展取得显著成效,商业模式创新发展,消费结构升级持续发展,某主打线上零售产品的企业随机抽取了50名销售员,统计了其2020年的月均销售额(单位:万元),将数据按照[12,14),…,[22,24]分成6组,制成了如图所示的频率分布直方图.已知[14,16)组成频数比[12,14)组多4.
(1)求频率分布直方图中a和b的值;
(2)该企业为了挖掘销售员的工作潜力,对销售员实行冲刺目标管理,即给销售员确定一个具体的冲刺目标,完成这个冲刺目标,则给予额外的奖励,若公司希望恰有20%的销售人员能够获得额外奖励,求该企业该制定的月销售冲刺目标值.
15.如图是根据某市3月1日至3月10日的最低气温(单位:℃)的情况绘制的折线统计图,试根据折线统计图反映的信息,绘制该市3月1日到10日最低气温(单位:℃)的扇形统计图.
16.在学校开展的综合实践活动中,某班进行了小制作评比,作品上交时间为5月1日至30日,评委会把同学们上交作品的件数按5天一组分组统计,绘制了频率分布直方图(如图所示).已知从左到右各长方形的高的比为2∶3∶4∶6∶4∶1,第三组的频数为12,请解答下列问题:
(1)本次活动共有多少件作品参加评比?(2)哪组上交的作品数最多?有多少件?
(3)经过评比,第四组和第六组分别有10件、2件作品获奖,问这两组哪组获奖率较高?
参考答案及解析:
一、选择题
1.B 解析:由图表可知全县年人均收入为7 050>7 000,达到了标准①;全县年人均食品支出为2 695,而年人均食品支出占收入的×100%≈38.2%>35%,未达到标准②,所以不是小康县.故选B.
2.B 解析:根据频率分布直方图得,直径落在区间[5.43,5.47)内的频率为(6.25+5.00)×0.02=0.225,则直径落在区间[5.43,5.47)内的零件的个数为80×0.225=18.
3.C 解析:由图易知,乙的逻辑推理能力指标值为3分,而甲的逻辑推理能力指标值为4分,故A错误;甲的数学建模能力指标值为3分,乙的直观想象能力指标值为5分,故B错误;
乙的六维能力指标值有3项优于、1项等于甲的六维能力指标值,故C正确;甲的数学运算能力指标值为4分,而甲的直观想象能力指标值为5分,故D错误.
4.D 解析:由频率分布直方图可知每周自习时间不少于22.5小时的频率为(0.16+0.08+0.04)×2.5=0.7,故每周自习时间不少于22.5小时的人数为0.7×200=140.故选D.
5.C 6.B
7.A 解析:由题意可知,前三组的频率之和为(0.01+0.024+0.036)×10=0.7,
∴支出在[50,60]内的频率为1-0.7=0.3,∴n==100.
8.B 9.ABC
二、填空题
10.答案:0.0044 解析:∵(0.0024+0.0036+0.0060+x+0.0024+0.0012)×50=1,∴x=0.0044
11.答案:0.04,3,2,1 解析:由(0.01+0.02+a+0.06+0.07)×5=1,得a=0.04.
设第3,4,5组抽取的学生人数依次为x,y,z,则x∶y∶z=0.06∶0.04∶0.02=3∶2∶1,
又x+y+z=6,所以x=3,y=2,z=1.
12.答案:0.52 解析:样本数据落在[10,40)上的频数为13+24+15=52.则样本数据落在[10,40)上的频率为=0.52.
13.答案:24
解析:因为频率=,所以第二、四组的频数都为72×=16.所以第三组的频数为72-2×8-2×16=24.
三、解答题
14.解:(1)由题意得解得a=0.03,b=0.07.
(2)设应该制定的月销售冲刺目标值为x万元,则在频率分布直方图中x右边的面积为1-0.8=0.2.
最后一组的面积是0.04×2=0.08,最后两组的面积之和为0.10×2+0.04×2=0.28.
因为0.08<0.2<0.28,所以x位于倒数第二组,
则(22-x)×0.10+0.08=0.2,解得x=20.8.
所以该企业的月销售冲刺目标值应该定为20.8万元.
15.解:该城市3月1日至10日的最低气温(单位:℃)情况如下表:
日期 1 2 3 4 5 6 7 8 9 10
最低气温(℃) -3 -2 0 -1 1 2 0 -1 2 2
其中最低气温为-3 ℃的有1天,占10%,最低气温为-2 ℃的有1天,占10%,最低气温为-1℃的有2天,占20%,最低气温为0℃的有2天,占20%,最低气温为1℃的有1天,占10%,最低气温为2℃的有3天,占30%,扇形统计图如图所示.
16.解:(1)依题意知,第三组的频率为=
又∵第三组频数为12,∴本次活动的参评作品数为=60件.
(2)由频率分布直方图,可以看出第四组上交的作品数量最多,共有60×=18件.
(3)第四组获奖率是=
第六组上交的作品数为60×=3件.
∴第六组的获奖率是,显然第六组的获奖率较高.
一、选择题
1.对“小康县”的经济评价标准如下:①年人均收入不小于7 000元;
②年人均食品支出不大于收入的35%. 某县有40万人,调查数据如下:
年人均收入/元 0 2 000 4 000 6 000 8 000 10 000 12 000 16 000
人数/万人 6 3 5 5 6 7 5 3
则该县( )
A.是小康县 B.达到标准①,未达到标准②,不是小康县
C.两个标准都未达到,不是小康县 D.达到标准②,未达到标准①,不是小康县
2.从一批零件中抽取80个,测量其直径(单位:mm),将所得数据分为9组:[5.31,5.33),[5.33,5.35),…,[5.45,5.47),[5.47,5.49],并整理得到如图所示的频率分布直方图,则在被抽取的零件中,直径落在区间[5.43,5.47)内的个数为( )
A.10 B.18 C.20 D.36
3.比较甲、乙两名学生的数学学科素养的各项能力指标值(满分为5分,分值高者为优),绘制了如图所示的六维能力雷达图,例如图中甲的数学抽象能力指标值为4,乙的数学抽象能力指标值为5,则下面叙述正确的是( )
A.乙的逻辑推理能力指标值优于甲的逻辑推理能力指标值
B.甲的数学建模能力指标值优于乙的直观想象能力指标值
C.乙的六维能力指标值整体水平优于甲的六维能力指标值整体水平
D.甲的数学运算能力指标值优于甲的直观想象能力指标值
4.某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].根据直方图,这200名学生中每周的自习时间不少于22.5小时的人数是( )
A.56 B.60 C.120 D.140
5.随着2022年北京冬奥会临近,中国冰雪产业快速发展,冰雪运动人数快速上升,冰雪运动市场需求得到释放,将引领户外用品行业市场增长.如图是2012年至2018年中国雪场滑雪人次(单位:万)与同比增长率的统计图,则下列结论中不正确的是( )
A.2013年至2018年,中国雪场滑雪人次逐年增加
B.2013年至2015年,中国雪场滑雪人次和同比增长率均逐年增加
C.2018年与2013年相比,中国雪场滑雪人次的同比增长率近似相等,所以同比增长人数也近似相等
D.2018年与2016年相比,中国雪场滑雪人次增长率约为30.5%
6.一个容量为32的样本中,已知某组样本的频率为0.125,则该组样本的频数为( )
A.2 B.4 C.6 D.8
7.学校为了调查学生在课外读物方面的支出情况,抽取了一个容量为n的样本,其频率分布直方图如图所示,其中支出(单位:元)在[50,60]内的学生有30人,则n的值为( )
A.100 B.1 000 C.90 D.900
8.某公司2019年在各个项目中总投资500万元,如图是几类项目的投资占比情况,已知在1万元以上的项目投资中,少于3万元的项目投资占,那么不少于3万元的项目投资共有( )
A.56万元 B.65万元 C.91万元 D.147万元
9.(多选)如下统计表和如图所示的分布图取自《清华大学2019年毕业生就业质量报告》.
清华大学2019年毕业生去向分布情况统计表
毕业去向 本科生 硕士生 博士生 总体
人数 比例 人数 比例 人数 比例 人数 比例
深造(国内) 1 583 55.8% 94 3.8% 290 19.9% 1 967 29.0%
深造(出国) 699 24.6% 137 5.5% 199 13.7% 1 035 15.3%
就业(签三方就业) 154 5.4% 1 656 66.4% 864 59.4% 2 674 39.4%
就业(灵活就业) 336 11.8% 568 22.8% 79 5.4% 983 14.5%
未就业 64 2.3% 39 1.6% 23 1.6% 126 1.9%
合计 2 836 100.0% 2 494 100.0% 1 455 100.0% 6 785 100.0%
清华大学2019年毕业生签三方就业单位所在省(区、市)分布图
则下列选项正确的是( )
A.清华大学2019年毕业生中,大多数本科生选择继续深造,大多数硕士生选择就业
B.清华大学2019年毕业生中,硕士生的就业率比本科生高
C.清华大学2019年签三方就业的毕业生中,本科生的就业城市比硕士生的就业城市分散
D.清华大学2019年签三方就业的毕业生中,留北京人数超过一半
二、填空题
10.从某小区抽取100户居民进行月用电量调查,发现其用电量都在50至350度之间,频率分布直方图如图所示.则频率分布直方图中x的值为________
11.为了解学生的身体状况,某校随机抽取了一批学生测量体重.经统计,这批学生的体重数据(单位:千克)全部介于45至70之间.将数据分成以下5组:第1组[45,50),第2组[50,55),第3组[55,60),第4组[60,65),第5组[65,70],得到如图所示的频率分布直方图,则a=________.现采用分层随机抽样的方法,从第3,4,5组中随机抽取6名学生,则第3,4,5组抽取的学生人数依次为________
12.一个容量为100的样本,其数据的分组与各组的频数如下表:
组别 [0,10) [10,20) [20,30) [30,40) [40,50) [50,60) [60,70]
频数 12 13 24 15 16 13 7
则样本数据落在[10,40)上的频率为________
13.一个样本的容量为72,分成5组,已知第一、五组的频数都为8,第二、四组的频率都为,则第三组的频数为________
三、解答题
14.2020年,面对突如其来的新冠肺炎疫情中,在党中央领导下,各地区各部门统筹疫情防控和经济社会发展取得显著成效,商业模式创新发展,消费结构升级持续发展,某主打线上零售产品的企业随机抽取了50名销售员,统计了其2020年的月均销售额(单位:万元),将数据按照[12,14),…,[22,24]分成6组,制成了如图所示的频率分布直方图.已知[14,16)组成频数比[12,14)组多4.
(1)求频率分布直方图中a和b的值;
(2)该企业为了挖掘销售员的工作潜力,对销售员实行冲刺目标管理,即给销售员确定一个具体的冲刺目标,完成这个冲刺目标,则给予额外的奖励,若公司希望恰有20%的销售人员能够获得额外奖励,求该企业该制定的月销售冲刺目标值.
15.如图是根据某市3月1日至3月10日的最低气温(单位:℃)的情况绘制的折线统计图,试根据折线统计图反映的信息,绘制该市3月1日到10日最低气温(单位:℃)的扇形统计图.
16.在学校开展的综合实践活动中,某班进行了小制作评比,作品上交时间为5月1日至30日,评委会把同学们上交作品的件数按5天一组分组统计,绘制了频率分布直方图(如图所示).已知从左到右各长方形的高的比为2∶3∶4∶6∶4∶1,第三组的频数为12,请解答下列问题:
(1)本次活动共有多少件作品参加评比?(2)哪组上交的作品数最多?有多少件?
(3)经过评比,第四组和第六组分别有10件、2件作品获奖,问这两组哪组获奖率较高?
参考答案及解析:
一、选择题
1.B 解析:由图表可知全县年人均收入为7 050>7 000,达到了标准①;全县年人均食品支出为2 695,而年人均食品支出占收入的×100%≈38.2%>35%,未达到标准②,所以不是小康县.故选B.
2.B 解析:根据频率分布直方图得,直径落在区间[5.43,5.47)内的频率为(6.25+5.00)×0.02=0.225,则直径落在区间[5.43,5.47)内的零件的个数为80×0.225=18.
3.C 解析:由图易知,乙的逻辑推理能力指标值为3分,而甲的逻辑推理能力指标值为4分,故A错误;甲的数学建模能力指标值为3分,乙的直观想象能力指标值为5分,故B错误;
乙的六维能力指标值有3项优于、1项等于甲的六维能力指标值,故C正确;甲的数学运算能力指标值为4分,而甲的直观想象能力指标值为5分,故D错误.
4.D 解析:由频率分布直方图可知每周自习时间不少于22.5小时的频率为(0.16+0.08+0.04)×2.5=0.7,故每周自习时间不少于22.5小时的人数为0.7×200=140.故选D.
5.C 6.B
7.A 解析:由题意可知,前三组的频率之和为(0.01+0.024+0.036)×10=0.7,
∴支出在[50,60]内的频率为1-0.7=0.3,∴n==100.
8.B 9.ABC
二、填空题
10.答案:0.0044 解析:∵(0.0024+0.0036+0.0060+x+0.0024+0.0012)×50=1,∴x=0.0044
11.答案:0.04,3,2,1 解析:由(0.01+0.02+a+0.06+0.07)×5=1,得a=0.04.
设第3,4,5组抽取的学生人数依次为x,y,z,则x∶y∶z=0.06∶0.04∶0.02=3∶2∶1,
又x+y+z=6,所以x=3,y=2,z=1.
12.答案:0.52 解析:样本数据落在[10,40)上的频数为13+24+15=52.则样本数据落在[10,40)上的频率为=0.52.
13.答案:24
解析:因为频率=,所以第二、四组的频数都为72×=16.所以第三组的频数为72-2×8-2×16=24.
三、解答题
14.解:(1)由题意得解得a=0.03,b=0.07.
(2)设应该制定的月销售冲刺目标值为x万元,则在频率分布直方图中x右边的面积为1-0.8=0.2.
最后一组的面积是0.04×2=0.08,最后两组的面积之和为0.10×2+0.04×2=0.28.
因为0.08<0.2<0.28,所以x位于倒数第二组,
则(22-x)×0.10+0.08=0.2,解得x=20.8.
所以该企业的月销售冲刺目标值应该定为20.8万元.
15.解:该城市3月1日至10日的最低气温(单位:℃)情况如下表:
日期 1 2 3 4 5 6 7 8 9 10
最低气温(℃) -3 -2 0 -1 1 2 0 -1 2 2
其中最低气温为-3 ℃的有1天,占10%,最低气温为-2 ℃的有1天,占10%,最低气温为-1℃的有2天,占20%,最低气温为0℃的有2天,占20%,最低气温为1℃的有1天,占10%,最低气温为2℃的有3天,占30%,扇形统计图如图所示.
16.解:(1)依题意知,第三组的频率为=
又∵第三组频数为12,∴本次活动的参评作品数为=60件.
(2)由频率分布直方图,可以看出第四组上交的作品数量最多,共有60×=18件.
(3)第四组获奖率是=
第六组上交的作品数为60×=3件.
∴第六组的获奖率是,显然第六组的获奖率较高.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
