平行线[下学期]
图片预览






文档简介
课件17张PPT。平行线知识点1 平行线
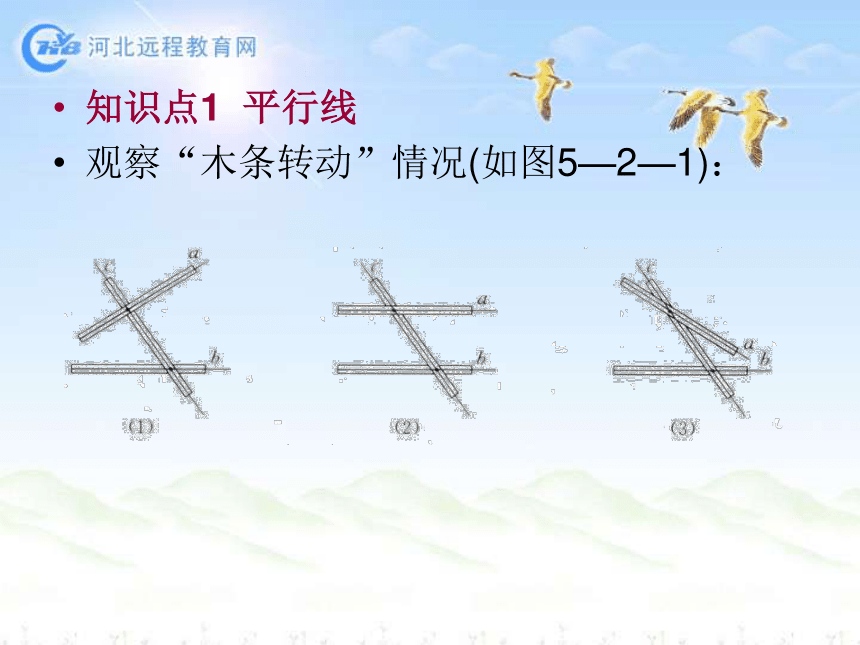
观察“木条转动”情况(如图5—2—1):固定木条b、c,转动木条a,并把它们想象成两端可以无限延长的三条直线。
发现:在木条转动过程中,存在一个直线a与直线b不相交的位置,这时直线a与b互相平行(parallel),记作a∥b。
由此看出:在同一平面内,不相交的两条直线称为平行线。注意:
(1)“在同一平面内”,就是说,平行线是在同一平面内而言的,这是一个很重要的前提;
(2)平行线指的是“两条直线”,而不是两条射线或线段;
(3)“不相交”,就是说两条直线没有交点。(4)平行线是指在同一平面内的具有特殊位置关系的两条直线,特殊在这两条直线没有交点。
(5)今后遇到线段、射线平行时,特指线段、射线所在的直线平行。
注意;平行线是相互的,使用符号表示时,AB∥CD也可以写成CD∥AB。知识点2 同一平面内,两条直线的位置关系
由上面“转动木条”活动,可看出:不重合的两条直线的位置关系有两种:①相交;②平行(请你动手画一画)。
注意:
①我们把重合后的两条直线认为是同一条直线。
②在同一平面内,如果两条直线不相交,那么它们一定平行;反之,如果两条直线不平行,那么它们一定相交。知识点3 平行线的画法
已知点P是直线AB外一点,经过点P画一条直线,使它与直线AB平行。
画法:
如图5.2—2,
(1)把三角板的一边靠紧直线AB,再用直尺(或另一块三角板)靠紧三角板的另一边。
(2)沿直尺推动三角板,使原来和直线AB重合的一边经过点P。
(3)过三角板原来与直线AB重合的这条边画直线CD。
CD就是所要画的经过点P,且与直线AB平行的直线。
说明:画平行线是几何画图的基本技能之一,在今后的画图中,会常常遇到画平行线的问题,应该加强练习,熟练掌握。知识点4 平行公理及推论
(1)平行公理:经过直线外一点,有且只有一条直线与已知直线平行。
(2)推论:如果两条直线都和第三条直线平行,那么这两条直线也互相平行。
也就是说:如果b∥a,c∥a那么b∥c。如图5—2—2。知识点5 直线平行的条件
判定方法有三种:
方法1:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行,如图5—2—4中,若∠1=∠2(或∠3=∠4或∠5=∠6或∠7=∠8),则a∥b。方法2:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行。如图5—2—4中,若∠1=∠6(或∠4=∠7),则a∥b。
方法3:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行。如图5—2—4中,若∠1+∠4=180°(或∠6+∠7=180°),则a∥b。简记为:①同位角相等,两直线平行;②内错角相等,两直线平行;③同旁内角互补,两直线平行。
注意:
(1)一定要看清哪两条直线被同一直线所截形成的同位角或内错角相等或同旁内角互补,才能正确判断是哪两条直线平行。
(2)在复杂图形中,要学会正确识别同位角、内错角、同旁内角。知识点6 判定两条直线平行的方法
由平行线的判定公理和判定定理可知,欲判定两条直线平行,只要能推出这两条直线被第三条直线所截成的同位角相等,或内错角相等,或同旁内角互补即可。此外,根据平行线的定义和平行公理的推论,还有两种判定方法:
①如果两条直线没有交点(不相交),那么两直线平行。②如果两条直线都平行于第三条直线,那么这两条直线平行。
注意:(1)平行线的判定公理,不但本身很重要,而且是推导其他两个判定定理的根据。
(2)证明(或解)过程中,填写理由时,一般都用简称。
观察“木条转动”情况(如图5—2—1):固定木条b、c,转动木条a,并把它们想象成两端可以无限延长的三条直线。
发现:在木条转动过程中,存在一个直线a与直线b不相交的位置,这时直线a与b互相平行(parallel),记作a∥b。
由此看出:在同一平面内,不相交的两条直线称为平行线。注意:
(1)“在同一平面内”,就是说,平行线是在同一平面内而言的,这是一个很重要的前提;
(2)平行线指的是“两条直线”,而不是两条射线或线段;
(3)“不相交”,就是说两条直线没有交点。(4)平行线是指在同一平面内的具有特殊位置关系的两条直线,特殊在这两条直线没有交点。
(5)今后遇到线段、射线平行时,特指线段、射线所在的直线平行。
注意;平行线是相互的,使用符号表示时,AB∥CD也可以写成CD∥AB。知识点2 同一平面内,两条直线的位置关系
由上面“转动木条”活动,可看出:不重合的两条直线的位置关系有两种:①相交;②平行(请你动手画一画)。
注意:
①我们把重合后的两条直线认为是同一条直线。
②在同一平面内,如果两条直线不相交,那么它们一定平行;反之,如果两条直线不平行,那么它们一定相交。知识点3 平行线的画法
已知点P是直线AB外一点,经过点P画一条直线,使它与直线AB平行。
画法:
如图5.2—2,
(1)把三角板的一边靠紧直线AB,再用直尺(或另一块三角板)靠紧三角板的另一边。
(2)沿直尺推动三角板,使原来和直线AB重合的一边经过点P。
(3)过三角板原来与直线AB重合的这条边画直线CD。
CD就是所要画的经过点P,且与直线AB平行的直线。
说明:画平行线是几何画图的基本技能之一,在今后的画图中,会常常遇到画平行线的问题,应该加强练习,熟练掌握。知识点4 平行公理及推论
(1)平行公理:经过直线外一点,有且只有一条直线与已知直线平行。
(2)推论:如果两条直线都和第三条直线平行,那么这两条直线也互相平行。
也就是说:如果b∥a,c∥a那么b∥c。如图5—2—2。知识点5 直线平行的条件
判定方法有三种:
方法1:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行,如图5—2—4中,若∠1=∠2(或∠3=∠4或∠5=∠6或∠7=∠8),则a∥b。方法2:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行。如图5—2—4中,若∠1=∠6(或∠4=∠7),则a∥b。
方法3:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行。如图5—2—4中,若∠1+∠4=180°(或∠6+∠7=180°),则a∥b。简记为:①同位角相等,两直线平行;②内错角相等,两直线平行;③同旁内角互补,两直线平行。
注意:
(1)一定要看清哪两条直线被同一直线所截形成的同位角或内错角相等或同旁内角互补,才能正确判断是哪两条直线平行。
(2)在复杂图形中,要学会正确识别同位角、内错角、同旁内角。知识点6 判定两条直线平行的方法
由平行线的判定公理和判定定理可知,欲判定两条直线平行,只要能推出这两条直线被第三条直线所截成的同位角相等,或内错角相等,或同旁内角互补即可。此外,根据平行线的定义和平行公理的推论,还有两种判定方法:
①如果两条直线没有交点(不相交),那么两直线平行。②如果两条直线都平行于第三条直线,那么这两条直线平行。
注意:(1)平行线的判定公理,不但本身很重要,而且是推导其他两个判定定理的根据。
(2)证明(或解)过程中,填写理由时,一般都用简称。
