热点07 锐角三角函数及其应用 (浙江专版) 中考三轮热点问题专题(含解析)
文档属性
| 名称 | 热点07 锐角三角函数及其应用 (浙江专版) 中考三轮热点问题专题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-26 00:00:00 | ||
图片预览



文档简介
浙江专版 中考三轮热点问题专题
热点07锐角三角函数及其应用
一.选择题
1.(2023 义乌市校级模拟)在Rt△ABC中,∠C=Rt∠,下列等式不一定成立的( )
A.a=csinA B.a=btanA C. D.sin2A+sin2B=1
2.(2023 永康市一模)一沙滩球网支架示意图如图所示,AB=AC=a米,∠ABC=α,则最高点A离地面BC的高度为( )
A.米 B.米 C.acosα米 D.asinα米
3.(2023 温州二模)如图是一个长方体柜子的俯视图,柜子长AB=CD=m(不计柜门厚度),当柜门打开的角度为α时,柜门打开的距离EF的长度为( )
A.msinα B.mcosα C. D.
4.(2023 上城区一模)如图,一只正方体箱子沿着斜面CD向上运动,∠C=α,箱高AB=1米,当BC=2米时,点A离地面CE的距离是( )米.
A. B. C.cosα+2sinα D.2cosα+sinα
5.(2023 龙湾区一模)如图,一个钟摆的摆长OB为1.5米,当钟摆向两边摆动时,摆角∠BOD为2a,且两边的摆动角度相同,则它摆至最高位置与其摆至最低位置时的高度之差AC为( )
A.(1.5﹣1.5cosα)米 B.米
C.(1.5﹣1.5sinα)米 D.米
6.(2023 瓯海区一模)如图,一把梯子AB斜靠在墙上,端点A离地面的高度AC长为1m时,∠ABC=45°.当梯子底端点B水平向左移动到点B',端点A沿墙竖直向上移动到点A',设∠A'B'C=α,则AA'的长可以表示为( )m.
A. B. C. D.
7.(2023 金华模拟)消防云梯如图所示,AB⊥BC于B,当C点刚好在A点的正上方时,DF的长是( )
A.acosθ+bsinθ B.acosθ+btanθ C. D.
8.(2023 鹿城区校级二模)一配电房示意图如图所示,它是一个轴对称图形.已知BC=6m,∠ABC=α,则房顶A离地面EF的高度为( )
A.(4+3sinα)m B.(4+3tanα)m C.(4+)m D.(4+)m
9.(2023 秀洲区校级一模)如图,在平面直角坐标系中,第一象限内的点P在射线OA上,OP=13,cosα=,则点P的坐标为( )
A.(5,13) B.(5,12) C.(13,5) D.(12,5)
10.(2023 东阳市三模)如图,在△ABC中,∠A=88°,∠C=42°,AB=60,则点A到BC的距离为( )
A.60sin50° B. C.60cos50° D.60tan50°
二.填空题
11.(2023 杭州一模)在Rt△ABC中,∠C=90°,BC=8,AB=10,sinB= .
12.(2023 鄞州区校级模拟)如图,在△ABC中,AD⊥BC,BD=5,CD=3,,则线段AD的长 .
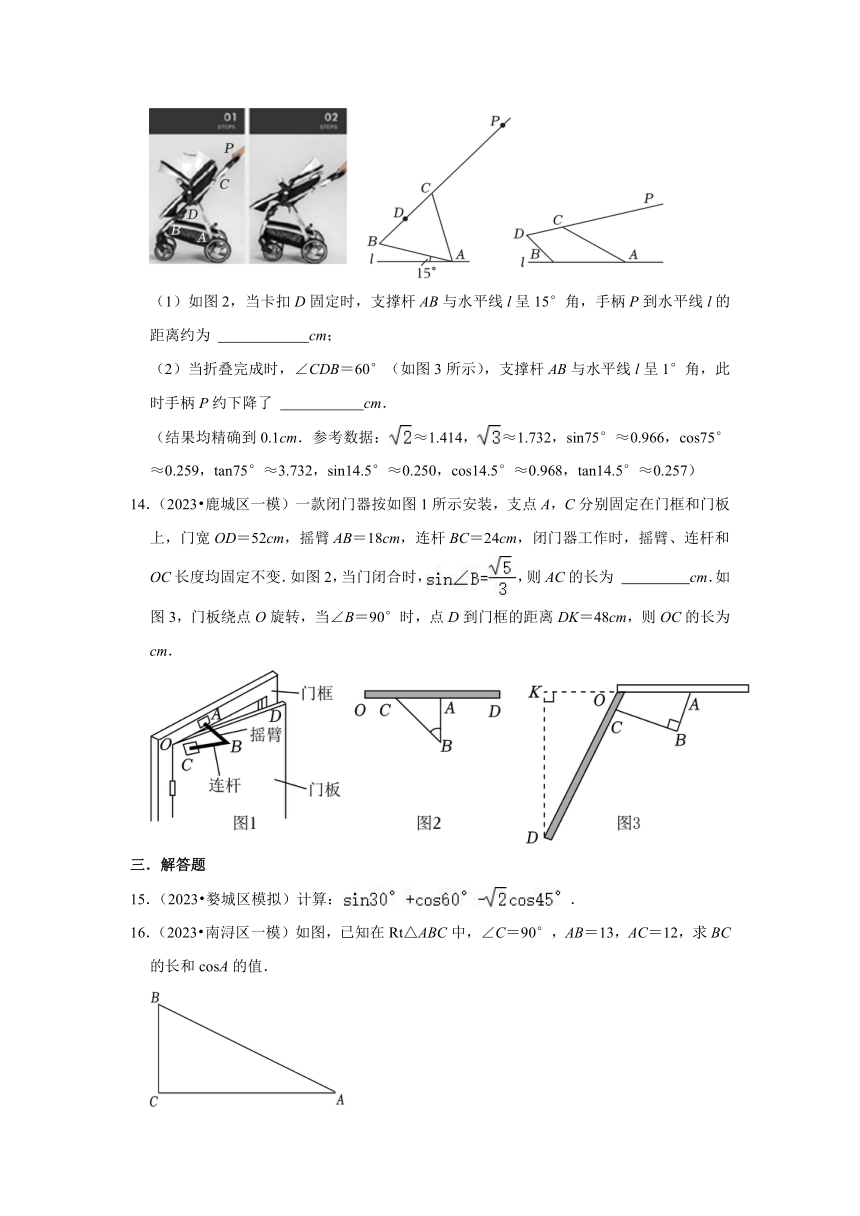
13.(2023 永康市一模)如图1为一款折叠婴儿车的演示过程.点D处有一卡扣,打开卡扣,从手柄P点处往下按压,完成折叠.已知支撑杆AB=AC=60cm,BD=30cm,卡扣D恰好为BC中点,推杆PD=110cm.
(1)如图2,当卡扣D固定时,支撑杆AB与水平线l呈15°角,手柄P到水平线l的距离约为 cm;
(2)当折叠完成时,∠CDB=60°(如图3所示),支撑杆AB与水平线l呈1°角,此时手柄P约下降了 cm.
(结果均精确到0.1cm.参考数据:≈1.414,≈1.732,sin75°≈0.966,cos75°≈0.259,tan75°≈3.732,sin14.5°≈0.250,cos14.5°≈0.968,tan14.5°≈0.257)
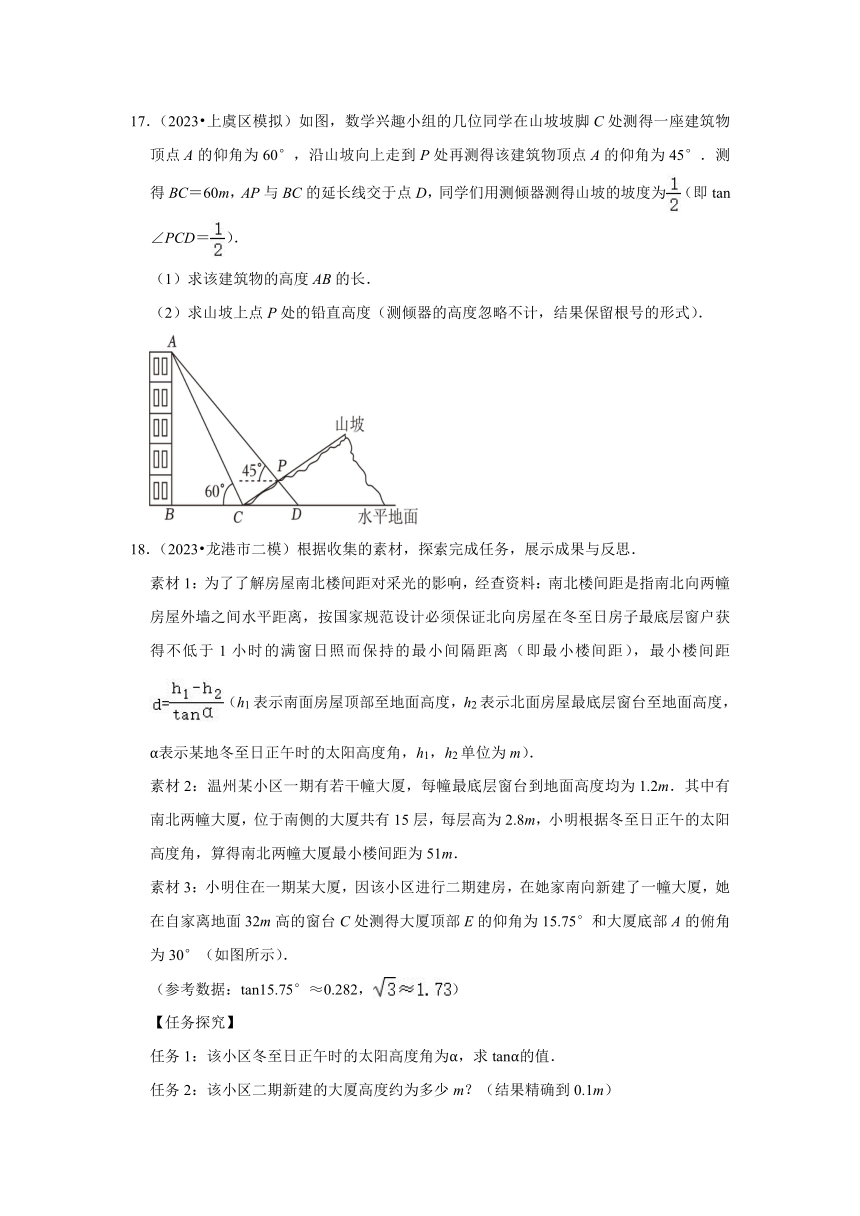
14.(2023 鹿城区一模)一款闭门器按如图1所示安装,支点A,C分别固定在门框和门板上,门宽OD=52cm,摇臂AB=18cm,连杆BC=24cm,闭门器工作时,摇臂、连杆和OC长度均固定不变.如图2,当门闭合时,,则AC的长为 cm.如图3,门板绕点O旋转,当∠B=90°时,点D到门框的距离DK=48cm,则OC的长为 cm.
三.解答题
15.(2023 婺城区模拟)计算:.
16.(2023 南浔区一模)如图,已知在Rt△ABC中,∠C=90°,AB=13,AC=12,求BC的长和cosA的值.
17.(2023 上虞区模拟)如图,数学兴趣小组的几位同学在山坡坡脚C处测得一座建筑物顶点A的仰角为60°,沿山坡向上走到P处再测得该建筑物顶点A的仰角为45°.测得BC=60m,AP与BC的延长线交于点D,同学们用测倾器测得山坡的坡度为(即tan∠PCD=).
(1)求该建筑物的高度AB的长.
(2)求山坡上点P处的铅直高度(测倾器的高度忽略不计,结果保留根号的形式).
18.(2023 龙港市二模)根据收集的素材,探索完成任务,展示成果与反思.
素材1:为了了解房屋南北楼间距对采光的影响,经查资料:南北楼间距是指南北向两幢房屋外墙之间水平距离,按国家规范设计必须保证北向房屋在冬至日房子最底层窗户获得不低于1小时的满窗日照而保持的最小间隔距离(即最小楼间距),最小楼间距(h1表示南面房屋顶部至地面高度,h2表示北面房屋最底层窗台至地面高度,α表示某地冬至日正午时的太阳高度角,h1,h2单位为m).
素材2:温州某小区一期有若干幢大厦,每幢最底层窗台到地面高度均为1.2m.其中有南北两幢大厦,位于南侧的大厦共有15层,每层高为2.8m,小明根据冬至日正午的太阳高度角,算得南北两幢大厦最小楼间距为51m.
素材3:小明住在一期某大厦,因该小区进行二期建房,在她家南向新建了一幢大厦,她在自家离地面32m高的窗台C处测得大厦顶部E的仰角为15.75°和大厦底部A的俯角为30°(如图所示).
(参考数据:tan15.75°≈0.282,)
【任务探究】
任务1:该小区冬至日正午时的太阳高度角为α,求tanα的值.
任务2:该小区二期新建的大厦高度约为多少m?(结果精确到0.1m)
【成果与反思】二期新建的大厦共有17层,每层高都相等.按国家规范设计冬至日房子窗户获得不低于1小时满窗日照的标准,请通过计算判断二期建房是否存在违规?如有违规,请提出至少需要拆除几层才能符合国家规范设计.
19.(2023 南湖区一模)如图1,一吸管杯放置在水平桌面上,矩形ABCD为其横截面,OE为吸管,其示意图如图2所示,AD=20cm,AB=6cm,OE=4cm,∠EOB=36°.
(1)当杯子盖上时,吸管OE绕点O按顺时针方向转动到OB处,求OE扫过的面积.
(2)当杯子绕点C按顺时针方向转动到OE与水平线CM平行时(如图3).
①求杯子与水平线CM的夹角∠BCM的度数.
②由图2到图3,点A的位置是升高了还是下降了?变化了多少厘米?(结果精确到0.1cm,参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73)
20.(2023 北仑区二模)如图为某校园的闸口,其双翼展开时为两个30°圆心角的扇形,PC=DQ=60cm,C、D处于同一水平线上且距离地面高度为18cm,CD水平距离为62cm.
(1)求A点距离地面的高度(精确到1cm);
(2)为了起到有效的阻隔作用,要求AB≤5cm,请通过计算说明该设备的安装是否符合要求.(参考数据)
21.(2023 秀洲区校级一模)小明学了《解直角三角形》内容后,对一条东西走向的隧道AB进行实地测量.如图所示,他在地面上点C处测得隧道一端点A在他的北偏东15°方向上,他沿西北方向前进100米后到达点D,此时测得点A在他的东北方向上,端点B在他的北偏西60°方向上,(点A、B、C、D在同一平面内)
(1)求点D与点A的距离;
(2)求隧道AB的长度.(结果保留根号)
22.(2023 绍兴模拟)某种落地灯如图1所示,AB为立杆,其高为70cm,BC为支杆,它可绕点B旋转,其中BC长为50cm,DE为悬杆,支杆BC与悬杆DE之间的夹角∠BCD为60°.
(1)如图2,当支杆BC与地面垂直,且灯泡悬挂点D距离地面的高度为100cm,求CD的长;
(2)在图2所示的状态下,将支杆BC绕点B顺时针旋转20°,如图3,求此时灯泡悬挂点D到地面的距离.(结果精确到1cm,参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)
答案与解析
一.选择题
1.(2023 义乌市校级模拟)在Rt△ABC中,∠C=Rt∠,下列等式不一定成立的( )
A.a=csinA B.a=btanA C. D.sin2A+sin2B=1
【点拨】根据三角函数的定义就可以解决.
【解析】解:A、∵sinA=,
∴a=csinA,故本选项不符合题意;
B、∵tanA=,
∴a=btanA,故本选项不符合题意;
C、∵cosB=,
∴c=,故本选项符合题意;
D、sin2A+sin2B=()2+()2===1,故本选项不符合题意;
故选:C.
【点睛】此题考查直角三角形中互余两角三角函数的关系,熟练掌握三角函数的定义是关键.
2.(2023 永康市一模)一沙滩球网支架示意图如图所示,AB=AC=a米,∠ABC=α,则最高点A离地面BC的高度为( )
A.米 B.米 C.acosα米 D.asinα米
【点拨】根据三角函数的定义即可得到结论.
【解析】解:∵AB=AC=a米,AD⊥BC,
∴在Rt△ABD中,∠ADB=90°,AD=AB sinα=asinα,
故选:D.
【点睛】本题主要考查了解直角三角形的应用,利用直角三角形的边角关系定理求得AD的长是解题的关键.
3.(2023 温州二模)如图是一个长方体柜子的俯视图,柜子长AB=CD=m(不计柜门厚度),当柜门打开的角度为α时,柜门打开的距离EF的长度为( )
A.msinα B.mcosα C. D.
【点拨】在Rt△AEF中利用直角三角形的边角间关系得结论.
【解析】解:由题意可知,AE=AB=m.
在Rt△AEF中,
∵sin∠EAB=,
∴EF=sinα m=msina.
故选:A.
【点睛】本题考查了解直角三角形,掌握直角三角形的边角间关系是解决本题的关键.
4.(2023 上城区一模)如图,一只正方体箱子沿着斜面CD向上运动,∠C=α,箱高AB=1米,当BC=2米时,点A离地面CE的距离是( )米.
A. B.
C.cosα+2sinα D.2cosα+sinα
【点拨】过点A作AG⊥CE,垂足为G,过点B作BH⊥CE于H,BM⊥AG,垂足为M,根据题意可得BH=GM,∠ABC=∠BHC=∠AGC=90°,再利用等角的余角相等可得∠C=∠BAF=α,然后在Rt△ABM中,利用锐角三角函数的定义求出AM的长,再在Rt△CBH中,利用锐角三角函数的定义求出BH的长,从而求出GM的长,最后进行计算即可解答.
【解析】解:过点A作AG⊥CE,垂足为G,过点B作BH⊥CE于H,BM⊥AG,垂足为M,
由题意得:BH=GM,∠ABC=∠BHC=∠AGC=90°,
∴∠C+∠CFG=90°,∠AFB+∠BAF=90°,
∵∠CFG=∠AFB,
∴∠C=∠BAF=α,
在Rt△ABM中,AB=1米,
∴AM=AB cosα=cosα(米),
在Rt△CBH中,BC=2米,
∴BH=BC sinα=2sinα(米),
∴GM=BH=2sinα米,
∴AG=AM+GM=(cosα+2sinα)米,
∴点A离地面CE的距离是(cosα+2sinα)米,
故选:C.
【点睛】本题考查了解直角三角形的应用,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
5.(2023 龙湾区一模)如图,一个钟摆的摆长OB为1.5米,当钟摆向两边摆动时,摆角∠BOD为2a,且两边的摆动角度相同,则它摆至最高位置与其摆至最低位置时的高度之差AC为( )
A.(1.5﹣1.5cosα)米 B.米
C.(1.5﹣1.5sinα)米 D.米
【点拨】根据题意可得:OA⊥BD,∠BOC=α,OB=OA=1.5米,然后在Rt△BOC中,利用锐角三角函数的定义求出OC的长,从而利用线段的和差关系进行计算即可解答.
【解析】解:由题意得:OA⊥BD,∠BOC=∠BOD= 2α=α,OB=OA=1.5米,
在Rt△BOC中,OC=OB cosα=1.5cosα,
∴AC=OA﹣OC=(1.5﹣1.5cosα)米,
故选:A.
【点睛】本题考查了解直角三角形的应用,熟练掌握锐角三角函数的定义是解题的关键.
6.(2023 瓯海区一模)如图,一把梯子AB斜靠在墙上,端点A离地面的高度AC长为1m时,∠ABC=45°.当梯子底端点B水平向左移动到点B',端点A沿墙竖直向上移动到点A',设∠A'B'C=α,则AA'的长可以表示为( )m.
A. B. C. D.
【点拨】根据题意可得:∠ACB=90°,AB=A′B′,然后在Rt△ACB中,利用锐角三角函数的定义求出AB的长,从而求出A′B′的长,再在Rt△A′CB′中,利用锐角三角函数的定义求出A′C的长,最后利用线段的和差关系,进行计算即可解答.
【解析】解:由题意得:∠ACB=90°,AB=A′B′,
在Rt△ACB中,AC=1m,∠ABC=45°,
∴AB===(m),
∴AB=A′B′=m,
在Rt△A′CB′中,∠A′B′C=α,
∴A′C=A′B′ sinα=sinα(m),
∴AA′=A′C﹣AC=(sinα﹣1)m,
故选:B.
【点睛】本题考查了解直角三角形的应用,熟练掌握锐角三角函数的定义是解题的关键.
7.(2023 金华模拟)消防云梯如图所示,AB⊥BC于B,当C点刚好在A点的正上方时,DF的长是( )
A.acosθ+bsinθ B.acosθ+btanθ
C. D.
【点拨】连接AC,根据题意可得AC=EF,∠CAB+θ=90°,再利用垂直定义可得∠ABC=90°,从而可得∠BAC+∠BCA=90°,进而可得∠BCA=θ,然后在Rt△ABC中,利用锐角三角函数的定义求出AC的长,从而求出EF的长,最后在Rt△CDE中,利用锐角三角函数的定义求出DE的长,进行计算即可解答.
【解析】解:连接AC,
则AC=EF,∠CAB+θ=90°,
∵AB⊥BC,
∴∠ABC=90°,
∴∠BAC+∠BCA=90°,
∴∠BCA=θ,
在Rt△ABC中,BC=a,
∴AC==,
∴EF=AC=,
在Rt△CDE中,∠DCE=θ,CD=b,
∴DE=CD sinθ=bsinθ,
∴DF=DE+EF=bsinθ+,
故选:C.
【点睛】本题考查了解直角三角形的应用,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
8.(2023 鹿城区校级二模)一配电房示意图如图所示,它是一个轴对称图形.已知BC=6m,∠ABC=α,则房顶A离地面EF的高度为( )
A.(4+3sinα)m B.(4+3tanα)m C.(4+)m D.(4+)m
【点拨】过点A作AD⊥BC于点D,利用直角三角形的边角关系定理求得AD,.用AD+BE即可表示出房顶A离地面EF的高度.
【解析】解:过点A作AD⊥BC于点D,如图,
∵它是一个轴对称图形,
∴AB=AC,
∵AD⊥BC,
∴BD=BC=3m,
在Rt△ADB中,
∵tan∠ABC=,
∴AD=BD tanα=3tanαm.
∴房顶A离地面EF的高度=AD+BE=(4+3tanα)m,
故选:B.
【点睛】本题主要考查了解直角三角形的意义,轴对称的性质,等腰三角形的三线合一,利用直角三角形的边角关系定理求得AD的长是解题的关键.
9.(2023 秀洲区校级一模)如图,在平面直角坐标系中,第一象限内的点P在射线OA上,OP=13,cosα=,则点P的坐标为( )
A.(5,13) B.(5,12) C.(13,5) D.(12,5)
【点拨】过点P作PE⊥x轴于点E.根据a的余弦值和OP,先求出OE,再利用勾股定理求出PE即可.
【解析】解:如图,过点P作PE⊥x轴于点E.
设点P的坐标为(x,y),
则OE=x,PE=y.
在Rt△OPE中,
∵cosα==,OP=13,
∴OE=5.
∴PE==12.
∴P点的坐标为(5,12).
故选:B.
【点睛】本题考查了解直角三角形和勾股定理,掌握直角三角形的边角间关系是解决本题的关键.
10.(2023 东阳市三模)如图,在△ABC中,∠A=88°,∠C=42°,AB=60,则点A到BC的距离为( )
A.60sin50° B. C.60cos50° D.60tan50°
【点拨】过点A作AD⊥BC,通过三角形内角和定理求出∠B的度数,再在直角三角形中利用正弦求出点A到BC的距离.
【解析】解:过点作AD⊥BC,垂足为D,
在△ABC中,∠A=88°,∠C=42°,AB=60,
∴∠B=180°﹣88°﹣42°=50°,
在Rt△ADB中,sin50°=,
∴AD=60sin50°,
∴点A到BC的距离为60sin50°.
故选:A.
【点睛】本题考查了解直角三角形和点到直线的距离,解题的关键是掌握解直角三角形和点到直线的距离定义.
二.填空题
11.(2023 杭州一模)在Rt△ABC中,∠C=90°,BC=8,AB=10,sinB= .
【点拨】根据题意画出图形,由勾股定理求出BC的长,再由锐角三角函数的定义进行解答即可.
【解析】解:如图所示:
∵Rt△ABC中,∠C=90°,BC=8,AB=10,
∴AC=
=
=6,
∴sinB===.
故答案为:.
【点睛】本题考查的是锐角三角函数的定义,根据题意画出图形,利用数形结合求解是解答此题的关键.
12.(2023 鄞州区校级模拟)如图,在△ABC中,AD⊥BC,BD=5,CD=3,,则线段AD的长 2+3 .
【点拨】过B作BE⊥AC,垂足为E交AD于F,证明△AFE∽△BCE,推出,可得AF=6,由△BDF∽△ADC推出FD:DC=BD:AD,设FD长为x,由此构建方程求解x,进一步求得结果;
【解析】解:过B作BE⊥AC,垂足为E交AD于F,如图,
过B作BE⊥AC,垂足为E交AD于F,
∵tan∠BAE=,
∵∠C+∠EBC=90°,∠C+∠EAF=90°,
∴∠EAF=∠EBC,
∵∠AEF=∠BEC=90°
∴△AFE∽△BCE,
∴,
∵BC=BD+CD=8,
∴AF=6,
又∵∠BDF=∠ADC=90°,
∴△BDF∽△ADC,
∴FD:DC=BD:AD,
设FD长为x,则:
x:3=5:(x+6),
解得:x=2﹣3或﹣2﹣3(舍去),
∴AD=AF+FD=6+2﹣3=2+3.
故答案为:2+3.
【点睛】本题考查了解直角三角形,解决问题的关键是作辅助线构造相似三角形.
13.(2023 永康市一模)如图1为一款折叠婴儿车的演示过程.点D处有一卡扣,打开卡扣,从手柄P点处往下按压,完成折叠.已知支撑杆AB=AC=60cm,BD=30cm,卡扣D恰好为BC中点,推杆PD=110cm.
(1)如图2,当卡扣D固定时,支撑杆AB与水平线l呈15°角,手柄P到水平线l的距离约为 114.5 cm;
(2)当折叠完成时,∠CDB=60°(如图3所示),支撑杆AB与水平线l呈1°角,此时手柄P约下降了 64.5 cm.
(结果均精确到0.1cm.参考数据:≈1.414,≈1.732,sin75°≈0.966,cos75°≈0.259,tan75°≈3.732,sin14.5°≈0.250,cos14.5°≈0.968,tan14.5°≈0.257)
【点拨】(1)过点P作PF⊥l于点F,延长PB交l于点E,连接AD,得出△ABC是等边三角形,∠PEF=45°,在Rt△ABD中,,,则,进而根据EF=PF=,即可求解;
(2)连接BC,过点A作AM⊥BC于点M,过点C作CE⊥l于点E,过点P作PF⊥l于点F,过点C作CN⊥PF于点N,则四边形CEFN是矩形,根据,得出∠CAM=14.5°,结合题意得出∠CAE=30°,∠PCN=∠PCA﹣∠ACN=44.5°﹣30°=14.5°,分别求得PN,NF,即可求解.
【解析】解:(1)如图所示,过点P作PF⊥l于点F,延长PB交l于点E,连接AD,
∵AB=AC=60,BD=30,卡扣D恰好为BC中点,
∴BC=2BD=60
∴△ABC是等边三角形,
∴∠CAB=60°,
∵D恰好为BC中点,
∴,AD⊥BC,
∵∠BAE=15°,
∴∠DAE=45°,
∵AD⊥BC,
∴∠PEF=45°,ED=AD,
在Rt△ABD中,,,
∴,
在Rt△PFE中,EF=PF=,
故答案为:114.5.
(2)如图所示,连接BC,过点A作AM⊥BC于点M,过点C作CE⊥l于点E,过点P作PF⊥l于点F,过点C作CN⊥PF于点N,
则四边形CEFN是矩形,
∵DC=DB,∠CDB=60°
∴△DCB是等边三角形,
∴CB=DB=DC=30,
∵AC=AB=60,AM⊥BC,
∴CM=BM=15,
∴,
∴∠CAM=14.5°,
∴∠CAB=29°,
∵∠BAE=1°,
∴∠CAE=30°,
∴,
∵∠DCB=60°,∠ACM=90°﹣∠CAM=90°﹣14.5°=75.5°,
∴∠PCA=180°﹣∠DCB﹣∠ACM=180°﹣60°﹣75.5°=44.5°,
∵CN∥EF,
∴∠NCA=∠CAE=30°,
∴∠PCN=∠PCA﹣∠ACN=44.5°﹣30°=14.5°,
∴PN=sin14.5°×PC≈0.25×(110﹣30)=20,
∴PF=PN+NF=30+20=50,
∴下降了114.5﹣50=64.5cm,
故答案为:64.5.
【点睛】本题考查了解直角三角形的应用,熟练掌握三角函数的定义是解题的关键.
14.(2023 鹿城区一模)一款闭门器按如图1所示安装,支点A,C分别固定在门框和门板上,门宽OD=52cm,摇臂AB=18cm,连杆BC=24cm,闭门器工作时,摇臂、连杆和OC长度均固定不变.如图2,当门闭合时,,则AC的长为 18 cm.如图3,门板绕点O旋转,当∠B=90°时,点D到门框的距离DK=48cm,则OC的长为 8 cm.
【点拨】如图2,过点A作AE⊥BC于点E,根据锐角三角函数的定义可AE的长度,然后根据勾股定理即可求出AC的长度.如图3,连接AC,过点C作CE⊥AK于点E,由勾股定理可分别求出AC、OK的长度,然后利用相似三角形的性质可设OE=5x(cm),CE=12x(cm),OC=13x(cm),再根据勾股定理列出方程即可求出x的值.
【解析】解:如图2,过点A作AE⊥BC于点E,
在Rt△AEB中,
sinB=,
∴AE=AB sinB=18×=6(cm),
由勾股定理可知:BE==12(cm),
∴CE=CB﹣BE=24﹣12=12(cm),
在Rt△ACE中,
由勾股定理可知:AC==18cm(cm).
如图3,连接AC,过点C作CE⊥AK于点E,
在Rt△KOD中,
KO==20(cm),
∵∠DKO=∠CEO=90°,
∴DK∥CE,
∴△CEO∽△DKE,
∴==,
故设OE=5x(cm),CE=12x(cm),OC=13x(cm),
∴OA=OC+AC=(13x+18)(cm),
∴EA=OE+OA=(18x+18)(cm),
在Rt△ABC中,
由勾股定理可知:AC==30(cm),
在Rt△ACE中,
由勾股定理可知:(12x)2+(18x+18)2=302,
解得:x=﹣2(舍去)或x=,
∴OC=13x=8(cm),
故答案为:18,8.
【点睛】本题考查解直角三角形的应用,解题的关键是熟练运用锐角三角函数的定义以及勾股定理,本题属于中等题型.
三.解答题
15.(2023 婺城区模拟)计算:.
【点拨】根据特殊角的三角函数值解决此题即可.
【解析】解:原式=+﹣×
=1﹣1
=0.
【点睛】本题主要考查特殊角的三角函数值,熟练掌握特殊角的三角函数值是解决本题的关键.
16.(2023 南浔区一模)如图,已知在Rt△ABC中,∠C=90°,AB=13,AC=12,求BC的长和cosA的值.
【点拨】根据勾股定理以及锐角三角函数的定义即可求出答案.
【解析】解:在Rt△ABC中,∠C=90°,
由勾股定理可知:BC===5,
cosA==.
【点睛】本题考查解直角三角形,解题的关键是熟练运用勾股定理以及锐角三角函数的定义,本题属于基础题型.
17.(2023 上虞区模拟)如图,数学兴趣小组的几位同学在山坡坡脚C处测得一座建筑物顶点A的仰角为60°,沿山坡向上走到P处再测得该建筑物顶点A的仰角为45°.测得BC=60m,AP与BC的延长线交于点D,同学们用测倾器测得山坡的坡度为(即tan∠PCD=).
(1)求该建筑物的高度AB的长.
(2)求山坡上点P处的铅直高度(测倾器的高度忽略不计,结果保留根号的形式).
【点拨】(1)直接利用正切函数的定义列式求值即可;
(2)过点P作PH⊥BD于点H,过点P作PM⊥AB于点M.设PH=x,利用三角函数关系设法用x表示AM和PM,再利用AM=PM列方程求解即可.
【解析】解:(1)在Rt△ABC中,
BC=60,∠ACB=60°,
∴,
即,
∴.
答:该建筑物的高度AB的长为m.
(2)如图,过点P作PH⊥BD于点H,过点P作PM⊥AB于点M.
设PH=x.
在Rt△CPH中,
∵tan∠PCD==,
∴CH=2x,BM=PH=x,
又∵∠APM=45°,
∴AM=PM,
∴AB﹣BM=BC+CH,
即,
解得:.
∴山坡上点P处的铅直高度为.
【点睛】本题考查解直角三角形的应用﹣仰角俯角,解直角三角形的应用﹣坡度坡角,解题的关键是构造直角三角形,利用三角函数关系求值,或列方程求解.
18.(2023 龙港市二模)根据收集的素材,探索完成任务,展示成果与反思.
素材1:为了了解房屋南北楼间距对采光的影响,经查资料:南北楼间距是指南北向两幢房屋外墙之间水平距离,按国家规范设计必须保证北向房屋在冬至日房子最底层窗户获得不低于1小时的满窗日照而保持的最小间隔距离(即最小楼间距),最小楼间距(h1表示南面房屋顶部至地面高度,h2表示北面房屋最底层窗台至地面高度,α表示某地冬至日正午时的太阳高度角,h1,h2单位为m).
素材2:温州某小区一期有若干幢大厦,每幢最底层窗台到地面高度均为1.2m.其中有南北两幢大厦,位于南侧的大厦共有15层,每层高为2.8m,小明根据冬至日正午的太阳高度角,算得南北两幢大厦最小楼间距为51m.
素材3:小明住在一期某大厦,因该小区进行二期建房,在她家南向新建了一幢大厦,她在自家离地面32m高的窗台C处测得大厦顶部E的仰角为15.75°和大厦底部A的俯角为30°(如图所示).
(参考数据:tan15.75°≈0.282,)
【任务探究】
任务1:该小区冬至日正午时的太阳高度角为α,求tanα的值.
任务2:该小区二期新建的大厦高度约为多少m?(结果精确到0.1m)
【成果与反思】二期新建的大厦共有17层,每层高都相等.按国家规范设计冬至日房子窗户获得不低于1小时满窗日照的标准,请通过计算判断二期建房是否存在违规?如有违规,请提出至少需要拆除几层才能符合国家规范设计.
【点拨】任务1:把已知数据代入中计算即可;
任务2:由题意得AF=BC=32m,在Rt△AFC中,求出CF,在Rt△EFC中,求出EF即可求出大厦的高度;
【成果与反思】首先计算最小楼间距,判断是否存在违规建设,然后根据公式计算需要拆除的楼层即可.
【解析】解:任务1:由公式得:51=,
∴tanα=0.8;
任务2:由题意得AF=BC=32m,
在Rt△AFC中,(m),
在Rt△EFC中,EF=FC tan15.75°≈15.6(m),
∴大厦高EF=15.6+32≈47.6(m),
即该小区二期新建的大厦高度约为47.6米;
【成果与反思】
解:由最小楼间距d==58>55.36,
∴二期房屋存在违规建设.
设应拆除x个楼层,而每个楼层高为47.6÷17=2.8(m),
则 ≤55.36,
化简得2.8x≥2.112,
∵x为正整数,
∴x至少为1,
∴至少要拆除一个楼层.
【点睛】本题考查了解直角三角形的应用﹣仰角俯角问题,解决此类问题要了解角之间的关系,找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作高或垂线构造直角三角形,另当问题以一个实际问题的形式给出时,要善于读懂题意,把实际问题划归为直角三角形中边角关系问题加以解决.
19.(2023 南湖区一模)如图1,一吸管杯放置在水平桌面上,矩形ABCD为其横截面,OE为吸管,其示意图如图2所示,AD=20cm,AB=6cm,OE=4cm,∠EOB=36°.
(1)当杯子盖上时,吸管OE绕点O按顺时针方向转动到OB处,求OE扫过的面积.
(2)当杯子绕点C按顺时针方向转动到OE与水平线CM平行时(如图3).
①求杯子与水平线CM的夹角∠BCM的度数.
②由图2到图3,点A的位置是升高了还是下降了?变化了多少厘米?(结果精确到0.1cm,参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73)
【点拨】(1)根据扇形面积公式即可求解;
(2)①过点B作BF∥CM,根据平行线的性质即可求解;
②过点A作AG⊥CM于点G,延长AD交MC的延长线于点H,在Rt△HDC中,,在Rt△HAG中,∠HAG=90°﹣∠H=36°,,求得AG,即可求解.
【解析】解:(1)OE扫过的面积为,
(2)①如图所示,
过点B作BF∥CM,
∴OE∥BF,∠EOB=∠OBF=36°,
∴∠FBC=∠BCM,
∵∠ABC=∠ABF+∠FBC=90°,
∴∠BCM=∠FBC=90°﹣36°=54°;
②如图所示,
过点A作AG⊥CM于点G,延长AD交MC的延长线于点H,
∵AD∥BC,
∴∠H=∠BCM=54°,
∴∠DCH=36°,
在Rt△HDC中,,
∴DH=DCtan∠DCH=6tan36°,
∴AH=AD+DH=20+6tan36°,
在Rt△HAG中,∠HAG=90°﹣∠H=36°,,
∴AG=AH×cos36°=(20+6tan36°)cos36°,≈(20+6×0.73)×0.81≈19.7,
∴20﹣19.7=0.3cm;
点A的位置是下降了0.3厘米.
【点睛】本题考查了解直角三角形的应用,平行线的性质,求扇形面积,熟练掌握以上知识是解题的关键.
20.(2023 北仑区二模)如图为某校园的闸口,其双翼展开时为两个30°圆心角的扇形,PC=DQ=60cm,C、D处于同一水平线上且距离地面高度为18cm,CD水平距离为62cm.
(1)求A点距离地面的高度(精确到1cm);
(2)为了起到有效的阻隔作用,要求AB≤5cm,请通过计算说明该设备的安装是否符合要求.(参考数据)
【点拨】(1)过点A作 AM⊥PC,垂足为M,根据题意可得:AC=PC=60cm,然后在Rt△AMC中,利用锐角三角函数的定义求出CM的长,最后进行计算即可解答;
(2)过点B作BN⊥DQ,垂足为N,根据题意可得:BD=DQ=60cm,然后在Rt△AMC中,利用含30度角的直角三角形的性质求出AM的长,再在Rt△BDN中,利用含30度角的直角三角形的性质求出BN的长,最后进行计算即可解答.
【解析】解:(1)过点A作 AM⊥PC,垂足为M,
由题意得:AC=PC=60cm,
在Rt△AMC中,∠ACP=30°,
∴MC=AC cos30°=60×=30(cm),
∵C点距离地面的高度为 18cm,
∴A点距离地面的高度=30+18≈70(cm),
∴A点距离地面的高度约为70cm;
(2)该设备的安装符合要求,
理由:过点B作BN⊥DQ,垂足为N,
由题意得:BD=DQ=60cm,
在Rt△AMC中,AC=60cm,∠ACP=30°,
∴AM=AC=30(cm),
在Rt△BDN中,∠BDN=30°,
∴BN=BD=30(cm),
∵CD水平距离为62cm,
∴AB=62﹣AM﹣BN=62﹣30﹣30=2(cm),
∵2cm<5cm,
∴该设备的安装符合要求.
【点睛】本题考查了解直三角形的应用,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
21.(2023 秀洲区校级一模)小明学了《解直角三角形》内容后,对一条东西走向的隧道AB进行实地测量.如图所示,他在地面上点C处测得隧道一端点A在他的北偏东15°方向上,他沿西北方向前进100米后到达点D,此时测得点A在他的东北方向上,端点B在他的北偏西60°方向上,(点A、B、C、D在同一平面内)
(1)求点D与点A的距离;
(2)求隧道AB的长度.(结果保留根号)
【点拨】(1)根据方位角图,易知∠ACD=60°,∠ADC=90°,解Rt△ADC即可求解;
(2)过点D作DE⊥AB于点E.分别解Rt△ADE,Rt△BDE求出AE和BE,即可求出隧道AB的长.
【解析】解;(1)由题意可知:∠ACD=15°+45°=60°,∠ADC=180°﹣45°﹣45°=90°,
在Rt△ADC中,
∴(米),
答:点D与点A的距离为300米.
(2)过点D作DE⊥AB于点E,
∵AB是东西走向,
∴∠ADE=45°,∠BDE=60°,
在Rt△ADE中,
∴(米),
在Rt△BDE中,
∴(米),
∴(米),
答:隧道AB的长为米.
【点睛】本题考查了解直角三角形的应用﹣方向角问题,掌握方向角的概念,掌握特殊角的三角函数值是解题的关键.
22.(2023 绍兴模拟)某种落地灯如图1所示,AB为立杆,其高为70cm,BC为支杆,它可绕点B旋转,其中BC长为50cm,DE为悬杆,支杆BC与悬杆DE之间的夹角∠BCD为60°.
(1)如图2,当支杆BC与地面垂直,且灯泡悬挂点D距离地面的高度为100cm,求CD的长;
(2)在图2所示的状态下,将支杆BC绕点B顺时针旋转20°,如图3,求此时灯泡悬挂点D到地面的距离.(结果精确到1cm,参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)
【点拨】(1)过点D作DG⊥AC于点G,过点D作DF⊥AF于点F,从而可求出CG的长度,然后利用锐角三角函数的定义即可求出答案.
(2)过点D作DF⊥AF于点F,过点C作CH⊥AF于点H,过点D作DM⊥CH于点M,过点B作BN⊥CH于点N,从而可知四边形MDFH和四边形BNHA是矩形,利用锐角三角函数的定义可求出CN,CH,CM,MH的长度即可求出答案.
【解析】解:(1)过点D作DG⊥AC于点G,过点D作DF⊥AF于点F,
∴四边形GDFA是矩形,
∴GA=DF=100(cm),
∵CA=CB+BA,
∴CA=50+70=120(cm),
∴CG=CA﹣DF=120﹣100=20(cm),
∵∠BCD=60°,
∴∠CDG=30°,
∴CD=2CG=40(cm),
答:CD的长为40cm.
(2)过点D作DF⊥AF于点F,过点C作CH⊥AF于点H,
过点D作DM⊥CH于点M,过点B作BN⊥CH于点N,
∴四边形MDFH和四边形BNHA是矩形,
由题意可知:∠BCN=20°,∠BCD=60°,
∴∠MCD=60°﹣20°=40°,
在Rt△BCN中,
cos∠BCN=cos20°=,
∴CN=BCcos20°≈50×0.94≈47(cm),
∴CH=CN+NH=CN+AB=47+70=117(cm),
在Rt△CDM中,
∴cos∠MCD=cos40°=,
∴CM=CDcos40°≈40×0.77≈31(cm),
∴MH=CH﹣CM=117﹣31=86(cm),
答:此时灯泡悬挂点D到地面的距离为86cm.
【点睛】本题考查解直角三角形的应用,解题的关键是熟练运用锐角三角函数的定义,本题属于中等题型.
热点07锐角三角函数及其应用
一.选择题
1.(2023 义乌市校级模拟)在Rt△ABC中,∠C=Rt∠,下列等式不一定成立的( )
A.a=csinA B.a=btanA C. D.sin2A+sin2B=1
2.(2023 永康市一模)一沙滩球网支架示意图如图所示,AB=AC=a米,∠ABC=α,则最高点A离地面BC的高度为( )
A.米 B.米 C.acosα米 D.asinα米
3.(2023 温州二模)如图是一个长方体柜子的俯视图,柜子长AB=CD=m(不计柜门厚度),当柜门打开的角度为α时,柜门打开的距离EF的长度为( )
A.msinα B.mcosα C. D.
4.(2023 上城区一模)如图,一只正方体箱子沿着斜面CD向上运动,∠C=α,箱高AB=1米,当BC=2米时,点A离地面CE的距离是( )米.
A. B. C.cosα+2sinα D.2cosα+sinα
5.(2023 龙湾区一模)如图,一个钟摆的摆长OB为1.5米,当钟摆向两边摆动时,摆角∠BOD为2a,且两边的摆动角度相同,则它摆至最高位置与其摆至最低位置时的高度之差AC为( )
A.(1.5﹣1.5cosα)米 B.米
C.(1.5﹣1.5sinα)米 D.米
6.(2023 瓯海区一模)如图,一把梯子AB斜靠在墙上,端点A离地面的高度AC长为1m时,∠ABC=45°.当梯子底端点B水平向左移动到点B',端点A沿墙竖直向上移动到点A',设∠A'B'C=α,则AA'的长可以表示为( )m.
A. B. C. D.
7.(2023 金华模拟)消防云梯如图所示,AB⊥BC于B,当C点刚好在A点的正上方时,DF的长是( )
A.acosθ+bsinθ B.acosθ+btanθ C. D.
8.(2023 鹿城区校级二模)一配电房示意图如图所示,它是一个轴对称图形.已知BC=6m,∠ABC=α,则房顶A离地面EF的高度为( )
A.(4+3sinα)m B.(4+3tanα)m C.(4+)m D.(4+)m
9.(2023 秀洲区校级一模)如图,在平面直角坐标系中,第一象限内的点P在射线OA上,OP=13,cosα=,则点P的坐标为( )
A.(5,13) B.(5,12) C.(13,5) D.(12,5)
10.(2023 东阳市三模)如图,在△ABC中,∠A=88°,∠C=42°,AB=60,则点A到BC的距离为( )
A.60sin50° B. C.60cos50° D.60tan50°
二.填空题
11.(2023 杭州一模)在Rt△ABC中,∠C=90°,BC=8,AB=10,sinB= .
12.(2023 鄞州区校级模拟)如图,在△ABC中,AD⊥BC,BD=5,CD=3,,则线段AD的长 .
13.(2023 永康市一模)如图1为一款折叠婴儿车的演示过程.点D处有一卡扣,打开卡扣,从手柄P点处往下按压,完成折叠.已知支撑杆AB=AC=60cm,BD=30cm,卡扣D恰好为BC中点,推杆PD=110cm.
(1)如图2,当卡扣D固定时,支撑杆AB与水平线l呈15°角,手柄P到水平线l的距离约为 cm;
(2)当折叠完成时,∠CDB=60°(如图3所示),支撑杆AB与水平线l呈1°角,此时手柄P约下降了 cm.
(结果均精确到0.1cm.参考数据:≈1.414,≈1.732,sin75°≈0.966,cos75°≈0.259,tan75°≈3.732,sin14.5°≈0.250,cos14.5°≈0.968,tan14.5°≈0.257)
14.(2023 鹿城区一模)一款闭门器按如图1所示安装,支点A,C分别固定在门框和门板上,门宽OD=52cm,摇臂AB=18cm,连杆BC=24cm,闭门器工作时,摇臂、连杆和OC长度均固定不变.如图2,当门闭合时,,则AC的长为 cm.如图3,门板绕点O旋转,当∠B=90°时,点D到门框的距离DK=48cm,则OC的长为 cm.
三.解答题
15.(2023 婺城区模拟)计算:.
16.(2023 南浔区一模)如图,已知在Rt△ABC中,∠C=90°,AB=13,AC=12,求BC的长和cosA的值.
17.(2023 上虞区模拟)如图,数学兴趣小组的几位同学在山坡坡脚C处测得一座建筑物顶点A的仰角为60°,沿山坡向上走到P处再测得该建筑物顶点A的仰角为45°.测得BC=60m,AP与BC的延长线交于点D,同学们用测倾器测得山坡的坡度为(即tan∠PCD=).
(1)求该建筑物的高度AB的长.
(2)求山坡上点P处的铅直高度(测倾器的高度忽略不计,结果保留根号的形式).
18.(2023 龙港市二模)根据收集的素材,探索完成任务,展示成果与反思.
素材1:为了了解房屋南北楼间距对采光的影响,经查资料:南北楼间距是指南北向两幢房屋外墙之间水平距离,按国家规范设计必须保证北向房屋在冬至日房子最底层窗户获得不低于1小时的满窗日照而保持的最小间隔距离(即最小楼间距),最小楼间距(h1表示南面房屋顶部至地面高度,h2表示北面房屋最底层窗台至地面高度,α表示某地冬至日正午时的太阳高度角,h1,h2单位为m).
素材2:温州某小区一期有若干幢大厦,每幢最底层窗台到地面高度均为1.2m.其中有南北两幢大厦,位于南侧的大厦共有15层,每层高为2.8m,小明根据冬至日正午的太阳高度角,算得南北两幢大厦最小楼间距为51m.
素材3:小明住在一期某大厦,因该小区进行二期建房,在她家南向新建了一幢大厦,她在自家离地面32m高的窗台C处测得大厦顶部E的仰角为15.75°和大厦底部A的俯角为30°(如图所示).
(参考数据:tan15.75°≈0.282,)
【任务探究】
任务1:该小区冬至日正午时的太阳高度角为α,求tanα的值.
任务2:该小区二期新建的大厦高度约为多少m?(结果精确到0.1m)
【成果与反思】二期新建的大厦共有17层,每层高都相等.按国家规范设计冬至日房子窗户获得不低于1小时满窗日照的标准,请通过计算判断二期建房是否存在违规?如有违规,请提出至少需要拆除几层才能符合国家规范设计.
19.(2023 南湖区一模)如图1,一吸管杯放置在水平桌面上,矩形ABCD为其横截面,OE为吸管,其示意图如图2所示,AD=20cm,AB=6cm,OE=4cm,∠EOB=36°.
(1)当杯子盖上时,吸管OE绕点O按顺时针方向转动到OB处,求OE扫过的面积.
(2)当杯子绕点C按顺时针方向转动到OE与水平线CM平行时(如图3).
①求杯子与水平线CM的夹角∠BCM的度数.
②由图2到图3,点A的位置是升高了还是下降了?变化了多少厘米?(结果精确到0.1cm,参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73)
20.(2023 北仑区二模)如图为某校园的闸口,其双翼展开时为两个30°圆心角的扇形,PC=DQ=60cm,C、D处于同一水平线上且距离地面高度为18cm,CD水平距离为62cm.
(1)求A点距离地面的高度(精确到1cm);
(2)为了起到有效的阻隔作用,要求AB≤5cm,请通过计算说明该设备的安装是否符合要求.(参考数据)
21.(2023 秀洲区校级一模)小明学了《解直角三角形》内容后,对一条东西走向的隧道AB进行实地测量.如图所示,他在地面上点C处测得隧道一端点A在他的北偏东15°方向上,他沿西北方向前进100米后到达点D,此时测得点A在他的东北方向上,端点B在他的北偏西60°方向上,(点A、B、C、D在同一平面内)
(1)求点D与点A的距离;
(2)求隧道AB的长度.(结果保留根号)
22.(2023 绍兴模拟)某种落地灯如图1所示,AB为立杆,其高为70cm,BC为支杆,它可绕点B旋转,其中BC长为50cm,DE为悬杆,支杆BC与悬杆DE之间的夹角∠BCD为60°.
(1)如图2,当支杆BC与地面垂直,且灯泡悬挂点D距离地面的高度为100cm,求CD的长;
(2)在图2所示的状态下,将支杆BC绕点B顺时针旋转20°,如图3,求此时灯泡悬挂点D到地面的距离.(结果精确到1cm,参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)
答案与解析
一.选择题
1.(2023 义乌市校级模拟)在Rt△ABC中,∠C=Rt∠,下列等式不一定成立的( )
A.a=csinA B.a=btanA C. D.sin2A+sin2B=1
【点拨】根据三角函数的定义就可以解决.
【解析】解:A、∵sinA=,
∴a=csinA,故本选项不符合题意;
B、∵tanA=,
∴a=btanA,故本选项不符合题意;
C、∵cosB=,
∴c=,故本选项符合题意;
D、sin2A+sin2B=()2+()2===1,故本选项不符合题意;
故选:C.
【点睛】此题考查直角三角形中互余两角三角函数的关系,熟练掌握三角函数的定义是关键.
2.(2023 永康市一模)一沙滩球网支架示意图如图所示,AB=AC=a米,∠ABC=α,则最高点A离地面BC的高度为( )
A.米 B.米 C.acosα米 D.asinα米
【点拨】根据三角函数的定义即可得到结论.
【解析】解:∵AB=AC=a米,AD⊥BC,
∴在Rt△ABD中,∠ADB=90°,AD=AB sinα=asinα,
故选:D.
【点睛】本题主要考查了解直角三角形的应用,利用直角三角形的边角关系定理求得AD的长是解题的关键.
3.(2023 温州二模)如图是一个长方体柜子的俯视图,柜子长AB=CD=m(不计柜门厚度),当柜门打开的角度为α时,柜门打开的距离EF的长度为( )
A.msinα B.mcosα C. D.
【点拨】在Rt△AEF中利用直角三角形的边角间关系得结论.
【解析】解:由题意可知,AE=AB=m.
在Rt△AEF中,
∵sin∠EAB=,
∴EF=sinα m=msina.
故选:A.
【点睛】本题考查了解直角三角形,掌握直角三角形的边角间关系是解决本题的关键.
4.(2023 上城区一模)如图,一只正方体箱子沿着斜面CD向上运动,∠C=α,箱高AB=1米,当BC=2米时,点A离地面CE的距离是( )米.
A. B.
C.cosα+2sinα D.2cosα+sinα
【点拨】过点A作AG⊥CE,垂足为G,过点B作BH⊥CE于H,BM⊥AG,垂足为M,根据题意可得BH=GM,∠ABC=∠BHC=∠AGC=90°,再利用等角的余角相等可得∠C=∠BAF=α,然后在Rt△ABM中,利用锐角三角函数的定义求出AM的长,再在Rt△CBH中,利用锐角三角函数的定义求出BH的长,从而求出GM的长,最后进行计算即可解答.
【解析】解:过点A作AG⊥CE,垂足为G,过点B作BH⊥CE于H,BM⊥AG,垂足为M,
由题意得:BH=GM,∠ABC=∠BHC=∠AGC=90°,
∴∠C+∠CFG=90°,∠AFB+∠BAF=90°,
∵∠CFG=∠AFB,
∴∠C=∠BAF=α,
在Rt△ABM中,AB=1米,
∴AM=AB cosα=cosα(米),
在Rt△CBH中,BC=2米,
∴BH=BC sinα=2sinα(米),
∴GM=BH=2sinα米,
∴AG=AM+GM=(cosα+2sinα)米,
∴点A离地面CE的距离是(cosα+2sinα)米,
故选:C.
【点睛】本题考查了解直角三角形的应用,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
5.(2023 龙湾区一模)如图,一个钟摆的摆长OB为1.5米,当钟摆向两边摆动时,摆角∠BOD为2a,且两边的摆动角度相同,则它摆至最高位置与其摆至最低位置时的高度之差AC为( )
A.(1.5﹣1.5cosα)米 B.米
C.(1.5﹣1.5sinα)米 D.米
【点拨】根据题意可得:OA⊥BD,∠BOC=α,OB=OA=1.5米,然后在Rt△BOC中,利用锐角三角函数的定义求出OC的长,从而利用线段的和差关系进行计算即可解答.
【解析】解:由题意得:OA⊥BD,∠BOC=∠BOD= 2α=α,OB=OA=1.5米,
在Rt△BOC中,OC=OB cosα=1.5cosα,
∴AC=OA﹣OC=(1.5﹣1.5cosα)米,
故选:A.
【点睛】本题考查了解直角三角形的应用,熟练掌握锐角三角函数的定义是解题的关键.
6.(2023 瓯海区一模)如图,一把梯子AB斜靠在墙上,端点A离地面的高度AC长为1m时,∠ABC=45°.当梯子底端点B水平向左移动到点B',端点A沿墙竖直向上移动到点A',设∠A'B'C=α,则AA'的长可以表示为( )m.
A. B. C. D.
【点拨】根据题意可得:∠ACB=90°,AB=A′B′,然后在Rt△ACB中,利用锐角三角函数的定义求出AB的长,从而求出A′B′的长,再在Rt△A′CB′中,利用锐角三角函数的定义求出A′C的长,最后利用线段的和差关系,进行计算即可解答.
【解析】解:由题意得:∠ACB=90°,AB=A′B′,
在Rt△ACB中,AC=1m,∠ABC=45°,
∴AB===(m),
∴AB=A′B′=m,
在Rt△A′CB′中,∠A′B′C=α,
∴A′C=A′B′ sinα=sinα(m),
∴AA′=A′C﹣AC=(sinα﹣1)m,
故选:B.
【点睛】本题考查了解直角三角形的应用,熟练掌握锐角三角函数的定义是解题的关键.
7.(2023 金华模拟)消防云梯如图所示,AB⊥BC于B,当C点刚好在A点的正上方时,DF的长是( )
A.acosθ+bsinθ B.acosθ+btanθ
C. D.
【点拨】连接AC,根据题意可得AC=EF,∠CAB+θ=90°,再利用垂直定义可得∠ABC=90°,从而可得∠BAC+∠BCA=90°,进而可得∠BCA=θ,然后在Rt△ABC中,利用锐角三角函数的定义求出AC的长,从而求出EF的长,最后在Rt△CDE中,利用锐角三角函数的定义求出DE的长,进行计算即可解答.
【解析】解:连接AC,
则AC=EF,∠CAB+θ=90°,
∵AB⊥BC,
∴∠ABC=90°,
∴∠BAC+∠BCA=90°,
∴∠BCA=θ,
在Rt△ABC中,BC=a,
∴AC==,
∴EF=AC=,
在Rt△CDE中,∠DCE=θ,CD=b,
∴DE=CD sinθ=bsinθ,
∴DF=DE+EF=bsinθ+,
故选:C.
【点睛】本题考查了解直角三角形的应用,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
8.(2023 鹿城区校级二模)一配电房示意图如图所示,它是一个轴对称图形.已知BC=6m,∠ABC=α,则房顶A离地面EF的高度为( )
A.(4+3sinα)m B.(4+3tanα)m C.(4+)m D.(4+)m
【点拨】过点A作AD⊥BC于点D,利用直角三角形的边角关系定理求得AD,.用AD+BE即可表示出房顶A离地面EF的高度.
【解析】解:过点A作AD⊥BC于点D,如图,
∵它是一个轴对称图形,
∴AB=AC,
∵AD⊥BC,
∴BD=BC=3m,
在Rt△ADB中,
∵tan∠ABC=,
∴AD=BD tanα=3tanαm.
∴房顶A离地面EF的高度=AD+BE=(4+3tanα)m,
故选:B.
【点睛】本题主要考查了解直角三角形的意义,轴对称的性质,等腰三角形的三线合一,利用直角三角形的边角关系定理求得AD的长是解题的关键.
9.(2023 秀洲区校级一模)如图,在平面直角坐标系中,第一象限内的点P在射线OA上,OP=13,cosα=,则点P的坐标为( )
A.(5,13) B.(5,12) C.(13,5) D.(12,5)
【点拨】过点P作PE⊥x轴于点E.根据a的余弦值和OP,先求出OE,再利用勾股定理求出PE即可.
【解析】解:如图,过点P作PE⊥x轴于点E.
设点P的坐标为(x,y),
则OE=x,PE=y.
在Rt△OPE中,
∵cosα==,OP=13,
∴OE=5.
∴PE==12.
∴P点的坐标为(5,12).
故选:B.
【点睛】本题考查了解直角三角形和勾股定理,掌握直角三角形的边角间关系是解决本题的关键.
10.(2023 东阳市三模)如图,在△ABC中,∠A=88°,∠C=42°,AB=60,则点A到BC的距离为( )
A.60sin50° B. C.60cos50° D.60tan50°
【点拨】过点A作AD⊥BC,通过三角形内角和定理求出∠B的度数,再在直角三角形中利用正弦求出点A到BC的距离.
【解析】解:过点作AD⊥BC,垂足为D,
在△ABC中,∠A=88°,∠C=42°,AB=60,
∴∠B=180°﹣88°﹣42°=50°,
在Rt△ADB中,sin50°=,
∴AD=60sin50°,
∴点A到BC的距离为60sin50°.
故选:A.
【点睛】本题考查了解直角三角形和点到直线的距离,解题的关键是掌握解直角三角形和点到直线的距离定义.
二.填空题
11.(2023 杭州一模)在Rt△ABC中,∠C=90°,BC=8,AB=10,sinB= .
【点拨】根据题意画出图形,由勾股定理求出BC的长,再由锐角三角函数的定义进行解答即可.
【解析】解:如图所示:
∵Rt△ABC中,∠C=90°,BC=8,AB=10,
∴AC=
=
=6,
∴sinB===.
故答案为:.
【点睛】本题考查的是锐角三角函数的定义,根据题意画出图形,利用数形结合求解是解答此题的关键.
12.(2023 鄞州区校级模拟)如图,在△ABC中,AD⊥BC,BD=5,CD=3,,则线段AD的长 2+3 .
【点拨】过B作BE⊥AC,垂足为E交AD于F,证明△AFE∽△BCE,推出,可得AF=6,由△BDF∽△ADC推出FD:DC=BD:AD,设FD长为x,由此构建方程求解x,进一步求得结果;
【解析】解:过B作BE⊥AC,垂足为E交AD于F,如图,
过B作BE⊥AC,垂足为E交AD于F,
∵tan∠BAE=,
∵∠C+∠EBC=90°,∠C+∠EAF=90°,
∴∠EAF=∠EBC,
∵∠AEF=∠BEC=90°
∴△AFE∽△BCE,
∴,
∵BC=BD+CD=8,
∴AF=6,
又∵∠BDF=∠ADC=90°,
∴△BDF∽△ADC,
∴FD:DC=BD:AD,
设FD长为x,则:
x:3=5:(x+6),
解得:x=2﹣3或﹣2﹣3(舍去),
∴AD=AF+FD=6+2﹣3=2+3.
故答案为:2+3.
【点睛】本题考查了解直角三角形,解决问题的关键是作辅助线构造相似三角形.
13.(2023 永康市一模)如图1为一款折叠婴儿车的演示过程.点D处有一卡扣,打开卡扣,从手柄P点处往下按压,完成折叠.已知支撑杆AB=AC=60cm,BD=30cm,卡扣D恰好为BC中点,推杆PD=110cm.
(1)如图2,当卡扣D固定时,支撑杆AB与水平线l呈15°角,手柄P到水平线l的距离约为 114.5 cm;
(2)当折叠完成时,∠CDB=60°(如图3所示),支撑杆AB与水平线l呈1°角,此时手柄P约下降了 64.5 cm.
(结果均精确到0.1cm.参考数据:≈1.414,≈1.732,sin75°≈0.966,cos75°≈0.259,tan75°≈3.732,sin14.5°≈0.250,cos14.5°≈0.968,tan14.5°≈0.257)
【点拨】(1)过点P作PF⊥l于点F,延长PB交l于点E,连接AD,得出△ABC是等边三角形,∠PEF=45°,在Rt△ABD中,,,则,进而根据EF=PF=,即可求解;
(2)连接BC,过点A作AM⊥BC于点M,过点C作CE⊥l于点E,过点P作PF⊥l于点F,过点C作CN⊥PF于点N,则四边形CEFN是矩形,根据,得出∠CAM=14.5°,结合题意得出∠CAE=30°,∠PCN=∠PCA﹣∠ACN=44.5°﹣30°=14.5°,分别求得PN,NF,即可求解.
【解析】解:(1)如图所示,过点P作PF⊥l于点F,延长PB交l于点E,连接AD,
∵AB=AC=60,BD=30,卡扣D恰好为BC中点,
∴BC=2BD=60
∴△ABC是等边三角形,
∴∠CAB=60°,
∵D恰好为BC中点,
∴,AD⊥BC,
∵∠BAE=15°,
∴∠DAE=45°,
∵AD⊥BC,
∴∠PEF=45°,ED=AD,
在Rt△ABD中,,,
∴,
在Rt△PFE中,EF=PF=,
故答案为:114.5.
(2)如图所示,连接BC,过点A作AM⊥BC于点M,过点C作CE⊥l于点E,过点P作PF⊥l于点F,过点C作CN⊥PF于点N,
则四边形CEFN是矩形,
∵DC=DB,∠CDB=60°
∴△DCB是等边三角形,
∴CB=DB=DC=30,
∵AC=AB=60,AM⊥BC,
∴CM=BM=15,
∴,
∴∠CAM=14.5°,
∴∠CAB=29°,
∵∠BAE=1°,
∴∠CAE=30°,
∴,
∵∠DCB=60°,∠ACM=90°﹣∠CAM=90°﹣14.5°=75.5°,
∴∠PCA=180°﹣∠DCB﹣∠ACM=180°﹣60°﹣75.5°=44.5°,
∵CN∥EF,
∴∠NCA=∠CAE=30°,
∴∠PCN=∠PCA﹣∠ACN=44.5°﹣30°=14.5°,
∴PN=sin14.5°×PC≈0.25×(110﹣30)=20,
∴PF=PN+NF=30+20=50,
∴下降了114.5﹣50=64.5cm,
故答案为:64.5.
【点睛】本题考查了解直角三角形的应用,熟练掌握三角函数的定义是解题的关键.
14.(2023 鹿城区一模)一款闭门器按如图1所示安装,支点A,C分别固定在门框和门板上,门宽OD=52cm,摇臂AB=18cm,连杆BC=24cm,闭门器工作时,摇臂、连杆和OC长度均固定不变.如图2,当门闭合时,,则AC的长为 18 cm.如图3,门板绕点O旋转,当∠B=90°时,点D到门框的距离DK=48cm,则OC的长为 8 cm.
【点拨】如图2,过点A作AE⊥BC于点E,根据锐角三角函数的定义可AE的长度,然后根据勾股定理即可求出AC的长度.如图3,连接AC,过点C作CE⊥AK于点E,由勾股定理可分别求出AC、OK的长度,然后利用相似三角形的性质可设OE=5x(cm),CE=12x(cm),OC=13x(cm),再根据勾股定理列出方程即可求出x的值.
【解析】解:如图2,过点A作AE⊥BC于点E,
在Rt△AEB中,
sinB=,
∴AE=AB sinB=18×=6(cm),
由勾股定理可知:BE==12(cm),
∴CE=CB﹣BE=24﹣12=12(cm),
在Rt△ACE中,
由勾股定理可知:AC==18cm(cm).
如图3,连接AC,过点C作CE⊥AK于点E,
在Rt△KOD中,
KO==20(cm),
∵∠DKO=∠CEO=90°,
∴DK∥CE,
∴△CEO∽△DKE,
∴==,
故设OE=5x(cm),CE=12x(cm),OC=13x(cm),
∴OA=OC+AC=(13x+18)(cm),
∴EA=OE+OA=(18x+18)(cm),
在Rt△ABC中,
由勾股定理可知:AC==30(cm),
在Rt△ACE中,
由勾股定理可知:(12x)2+(18x+18)2=302,
解得:x=﹣2(舍去)或x=,
∴OC=13x=8(cm),
故答案为:18,8.
【点睛】本题考查解直角三角形的应用,解题的关键是熟练运用锐角三角函数的定义以及勾股定理,本题属于中等题型.
三.解答题
15.(2023 婺城区模拟)计算:.
【点拨】根据特殊角的三角函数值解决此题即可.
【解析】解:原式=+﹣×
=1﹣1
=0.
【点睛】本题主要考查特殊角的三角函数值,熟练掌握特殊角的三角函数值是解决本题的关键.
16.(2023 南浔区一模)如图,已知在Rt△ABC中,∠C=90°,AB=13,AC=12,求BC的长和cosA的值.
【点拨】根据勾股定理以及锐角三角函数的定义即可求出答案.
【解析】解:在Rt△ABC中,∠C=90°,
由勾股定理可知:BC===5,
cosA==.
【点睛】本题考查解直角三角形,解题的关键是熟练运用勾股定理以及锐角三角函数的定义,本题属于基础题型.
17.(2023 上虞区模拟)如图,数学兴趣小组的几位同学在山坡坡脚C处测得一座建筑物顶点A的仰角为60°,沿山坡向上走到P处再测得该建筑物顶点A的仰角为45°.测得BC=60m,AP与BC的延长线交于点D,同学们用测倾器测得山坡的坡度为(即tan∠PCD=).
(1)求该建筑物的高度AB的长.
(2)求山坡上点P处的铅直高度(测倾器的高度忽略不计,结果保留根号的形式).
【点拨】(1)直接利用正切函数的定义列式求值即可;
(2)过点P作PH⊥BD于点H,过点P作PM⊥AB于点M.设PH=x,利用三角函数关系设法用x表示AM和PM,再利用AM=PM列方程求解即可.
【解析】解:(1)在Rt△ABC中,
BC=60,∠ACB=60°,
∴,
即,
∴.
答:该建筑物的高度AB的长为m.
(2)如图,过点P作PH⊥BD于点H,过点P作PM⊥AB于点M.
设PH=x.
在Rt△CPH中,
∵tan∠PCD==,
∴CH=2x,BM=PH=x,
又∵∠APM=45°,
∴AM=PM,
∴AB﹣BM=BC+CH,
即,
解得:.
∴山坡上点P处的铅直高度为.
【点睛】本题考查解直角三角形的应用﹣仰角俯角,解直角三角形的应用﹣坡度坡角,解题的关键是构造直角三角形,利用三角函数关系求值,或列方程求解.
18.(2023 龙港市二模)根据收集的素材,探索完成任务,展示成果与反思.
素材1:为了了解房屋南北楼间距对采光的影响,经查资料:南北楼间距是指南北向两幢房屋外墙之间水平距离,按国家规范设计必须保证北向房屋在冬至日房子最底层窗户获得不低于1小时的满窗日照而保持的最小间隔距离(即最小楼间距),最小楼间距(h1表示南面房屋顶部至地面高度,h2表示北面房屋最底层窗台至地面高度,α表示某地冬至日正午时的太阳高度角,h1,h2单位为m).
素材2:温州某小区一期有若干幢大厦,每幢最底层窗台到地面高度均为1.2m.其中有南北两幢大厦,位于南侧的大厦共有15层,每层高为2.8m,小明根据冬至日正午的太阳高度角,算得南北两幢大厦最小楼间距为51m.
素材3:小明住在一期某大厦,因该小区进行二期建房,在她家南向新建了一幢大厦,她在自家离地面32m高的窗台C处测得大厦顶部E的仰角为15.75°和大厦底部A的俯角为30°(如图所示).
(参考数据:tan15.75°≈0.282,)
【任务探究】
任务1:该小区冬至日正午时的太阳高度角为α,求tanα的值.
任务2:该小区二期新建的大厦高度约为多少m?(结果精确到0.1m)
【成果与反思】二期新建的大厦共有17层,每层高都相等.按国家规范设计冬至日房子窗户获得不低于1小时满窗日照的标准,请通过计算判断二期建房是否存在违规?如有违规,请提出至少需要拆除几层才能符合国家规范设计.
【点拨】任务1:把已知数据代入中计算即可;
任务2:由题意得AF=BC=32m,在Rt△AFC中,求出CF,在Rt△EFC中,求出EF即可求出大厦的高度;
【成果与反思】首先计算最小楼间距,判断是否存在违规建设,然后根据公式计算需要拆除的楼层即可.
【解析】解:任务1:由公式得:51=,
∴tanα=0.8;
任务2:由题意得AF=BC=32m,
在Rt△AFC中,(m),
在Rt△EFC中,EF=FC tan15.75°≈15.6(m),
∴大厦高EF=15.6+32≈47.6(m),
即该小区二期新建的大厦高度约为47.6米;
【成果与反思】
解:由最小楼间距d==58>55.36,
∴二期房屋存在违规建设.
设应拆除x个楼层,而每个楼层高为47.6÷17=2.8(m),
则 ≤55.36,
化简得2.8x≥2.112,
∵x为正整数,
∴x至少为1,
∴至少要拆除一个楼层.
【点睛】本题考查了解直角三角形的应用﹣仰角俯角问题,解决此类问题要了解角之间的关系,找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作高或垂线构造直角三角形,另当问题以一个实际问题的形式给出时,要善于读懂题意,把实际问题划归为直角三角形中边角关系问题加以解决.
19.(2023 南湖区一模)如图1,一吸管杯放置在水平桌面上,矩形ABCD为其横截面,OE为吸管,其示意图如图2所示,AD=20cm,AB=6cm,OE=4cm,∠EOB=36°.
(1)当杯子盖上时,吸管OE绕点O按顺时针方向转动到OB处,求OE扫过的面积.
(2)当杯子绕点C按顺时针方向转动到OE与水平线CM平行时(如图3).
①求杯子与水平线CM的夹角∠BCM的度数.
②由图2到图3,点A的位置是升高了还是下降了?变化了多少厘米?(结果精确到0.1cm,参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73)
【点拨】(1)根据扇形面积公式即可求解;
(2)①过点B作BF∥CM,根据平行线的性质即可求解;
②过点A作AG⊥CM于点G,延长AD交MC的延长线于点H,在Rt△HDC中,,在Rt△HAG中,∠HAG=90°﹣∠H=36°,,求得AG,即可求解.
【解析】解:(1)OE扫过的面积为,
(2)①如图所示,
过点B作BF∥CM,
∴OE∥BF,∠EOB=∠OBF=36°,
∴∠FBC=∠BCM,
∵∠ABC=∠ABF+∠FBC=90°,
∴∠BCM=∠FBC=90°﹣36°=54°;
②如图所示,
过点A作AG⊥CM于点G,延长AD交MC的延长线于点H,
∵AD∥BC,
∴∠H=∠BCM=54°,
∴∠DCH=36°,
在Rt△HDC中,,
∴DH=DCtan∠DCH=6tan36°,
∴AH=AD+DH=20+6tan36°,
在Rt△HAG中,∠HAG=90°﹣∠H=36°,,
∴AG=AH×cos36°=(20+6tan36°)cos36°,≈(20+6×0.73)×0.81≈19.7,
∴20﹣19.7=0.3cm;
点A的位置是下降了0.3厘米.
【点睛】本题考查了解直角三角形的应用,平行线的性质,求扇形面积,熟练掌握以上知识是解题的关键.
20.(2023 北仑区二模)如图为某校园的闸口,其双翼展开时为两个30°圆心角的扇形,PC=DQ=60cm,C、D处于同一水平线上且距离地面高度为18cm,CD水平距离为62cm.
(1)求A点距离地面的高度(精确到1cm);
(2)为了起到有效的阻隔作用,要求AB≤5cm,请通过计算说明该设备的安装是否符合要求.(参考数据)
【点拨】(1)过点A作 AM⊥PC,垂足为M,根据题意可得:AC=PC=60cm,然后在Rt△AMC中,利用锐角三角函数的定义求出CM的长,最后进行计算即可解答;
(2)过点B作BN⊥DQ,垂足为N,根据题意可得:BD=DQ=60cm,然后在Rt△AMC中,利用含30度角的直角三角形的性质求出AM的长,再在Rt△BDN中,利用含30度角的直角三角形的性质求出BN的长,最后进行计算即可解答.
【解析】解:(1)过点A作 AM⊥PC,垂足为M,
由题意得:AC=PC=60cm,
在Rt△AMC中,∠ACP=30°,
∴MC=AC cos30°=60×=30(cm),
∵C点距离地面的高度为 18cm,
∴A点距离地面的高度=30+18≈70(cm),
∴A点距离地面的高度约为70cm;
(2)该设备的安装符合要求,
理由:过点B作BN⊥DQ,垂足为N,
由题意得:BD=DQ=60cm,
在Rt△AMC中,AC=60cm,∠ACP=30°,
∴AM=AC=30(cm),
在Rt△BDN中,∠BDN=30°,
∴BN=BD=30(cm),
∵CD水平距离为62cm,
∴AB=62﹣AM﹣BN=62﹣30﹣30=2(cm),
∵2cm<5cm,
∴该设备的安装符合要求.
【点睛】本题考查了解直三角形的应用,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
21.(2023 秀洲区校级一模)小明学了《解直角三角形》内容后,对一条东西走向的隧道AB进行实地测量.如图所示,他在地面上点C处测得隧道一端点A在他的北偏东15°方向上,他沿西北方向前进100米后到达点D,此时测得点A在他的东北方向上,端点B在他的北偏西60°方向上,(点A、B、C、D在同一平面内)
(1)求点D与点A的距离;
(2)求隧道AB的长度.(结果保留根号)
【点拨】(1)根据方位角图,易知∠ACD=60°,∠ADC=90°,解Rt△ADC即可求解;
(2)过点D作DE⊥AB于点E.分别解Rt△ADE,Rt△BDE求出AE和BE,即可求出隧道AB的长.
【解析】解;(1)由题意可知:∠ACD=15°+45°=60°,∠ADC=180°﹣45°﹣45°=90°,
在Rt△ADC中,
∴(米),
答:点D与点A的距离为300米.
(2)过点D作DE⊥AB于点E,
∵AB是东西走向,
∴∠ADE=45°,∠BDE=60°,
在Rt△ADE中,
∴(米),
在Rt△BDE中,
∴(米),
∴(米),
答:隧道AB的长为米.
【点睛】本题考查了解直角三角形的应用﹣方向角问题,掌握方向角的概念,掌握特殊角的三角函数值是解题的关键.
22.(2023 绍兴模拟)某种落地灯如图1所示,AB为立杆,其高为70cm,BC为支杆,它可绕点B旋转,其中BC长为50cm,DE为悬杆,支杆BC与悬杆DE之间的夹角∠BCD为60°.
(1)如图2,当支杆BC与地面垂直,且灯泡悬挂点D距离地面的高度为100cm,求CD的长;
(2)在图2所示的状态下,将支杆BC绕点B顺时针旋转20°,如图3,求此时灯泡悬挂点D到地面的距离.(结果精确到1cm,参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)
【点拨】(1)过点D作DG⊥AC于点G,过点D作DF⊥AF于点F,从而可求出CG的长度,然后利用锐角三角函数的定义即可求出答案.
(2)过点D作DF⊥AF于点F,过点C作CH⊥AF于点H,过点D作DM⊥CH于点M,过点B作BN⊥CH于点N,从而可知四边形MDFH和四边形BNHA是矩形,利用锐角三角函数的定义可求出CN,CH,CM,MH的长度即可求出答案.
【解析】解:(1)过点D作DG⊥AC于点G,过点D作DF⊥AF于点F,
∴四边形GDFA是矩形,
∴GA=DF=100(cm),
∵CA=CB+BA,
∴CA=50+70=120(cm),
∴CG=CA﹣DF=120﹣100=20(cm),
∵∠BCD=60°,
∴∠CDG=30°,
∴CD=2CG=40(cm),
答:CD的长为40cm.
(2)过点D作DF⊥AF于点F,过点C作CH⊥AF于点H,
过点D作DM⊥CH于点M,过点B作BN⊥CH于点N,
∴四边形MDFH和四边形BNHA是矩形,
由题意可知:∠BCN=20°,∠BCD=60°,
∴∠MCD=60°﹣20°=40°,
在Rt△BCN中,
cos∠BCN=cos20°=,
∴CN=BCcos20°≈50×0.94≈47(cm),
∴CH=CN+NH=CN+AB=47+70=117(cm),
在Rt△CDM中,
∴cos∠MCD=cos40°=,
∴CM=CDcos40°≈40×0.77≈31(cm),
∴MH=CH﹣CM=117﹣31=86(cm),
答:此时灯泡悬挂点D到地面的距离为86cm.
【点睛】本题考查解直角三角形的应用,解题的关键是熟练运用锐角三角函数的定义,本题属于中等题型.
同课章节目录
