四川省成都市城厢中学校2022-2023学年高二下学期期中考试数学(理)试题(Word版含答案)
文档属性
| 名称 | 四川省成都市城厢中学校2022-2023学年高二下学期期中考试数学(理)试题(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 680.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-26 13:00:06 | ||
图片预览

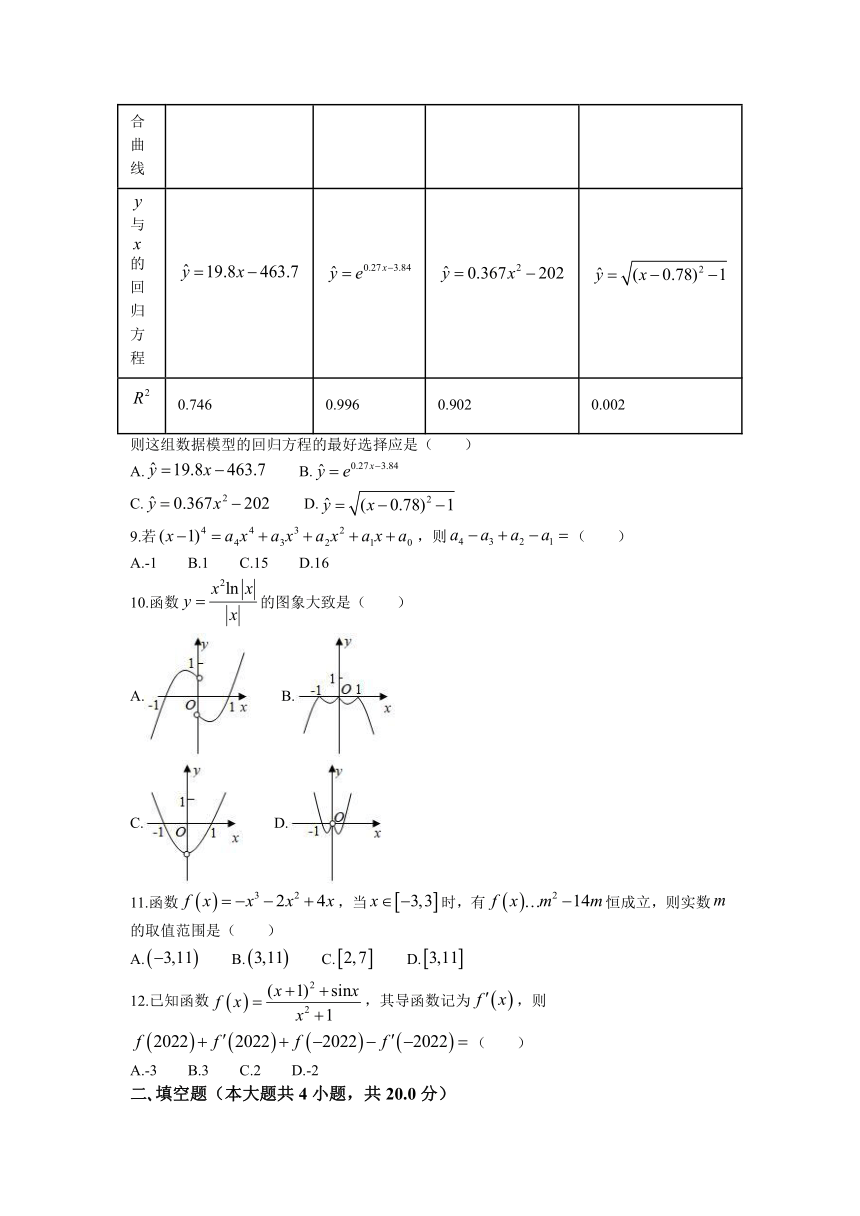

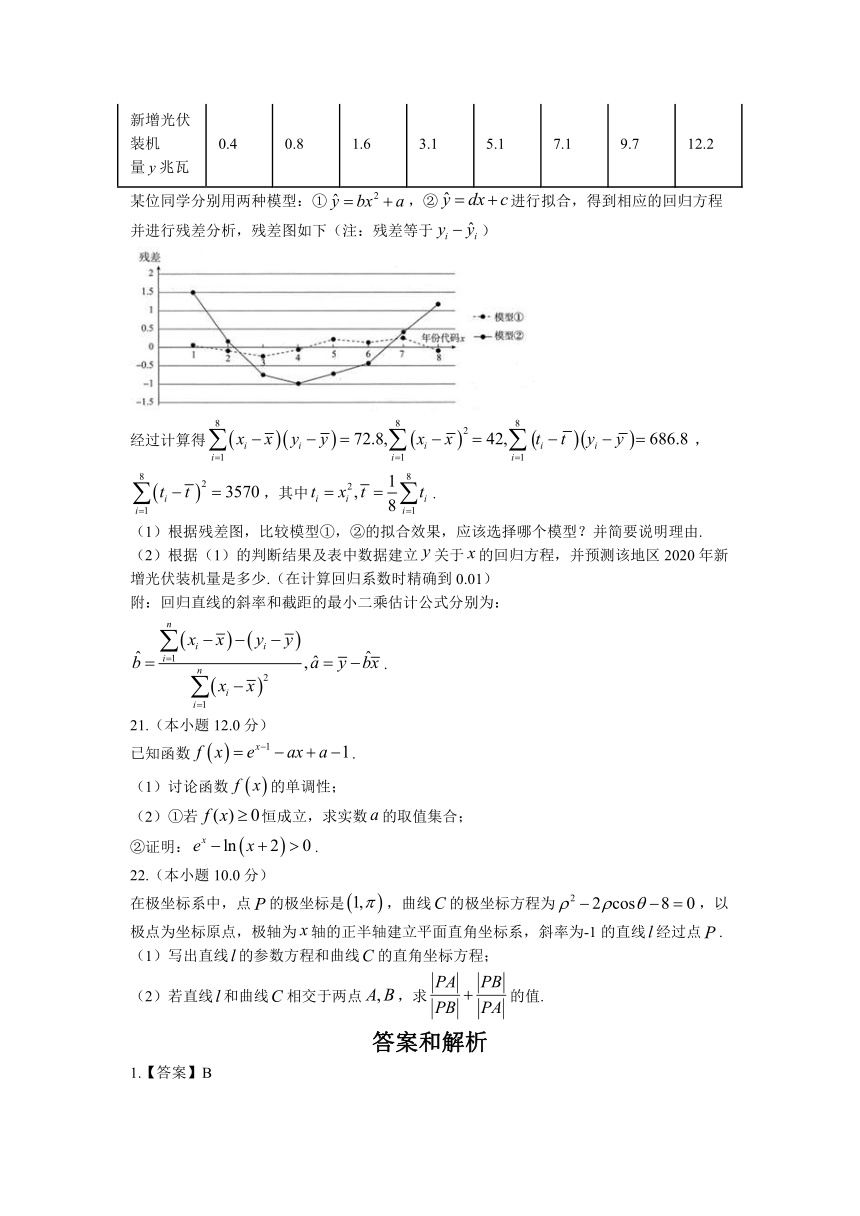

文档简介
城厢中学校2022-2023学年高二下学期期中考试
数学(理科)试卷
一 单选题(本大题共12小题,共60.0分.在每小题列出的选项中,选出符合题目的一项)
1.已知集合,则( )
A. B. C. D.
2.复数在复平面内表示的点的坐标为( )
A. B. C. D.
3.函数,则( )
A.-1 B.0 C. D.2
4.在极坐标系中,圆的圆心的极坐标是( )
A. B. C. D.
5.下列函数中,在定义域内既是奇函数又是增函数的是( )
A. B.
C. D.
6.执行如图所示的程序框图,输出的结果是( )
A.13 B.14 C.15 D.17
7.树立劳动观念对人的健康成长至关重要,某实践小组共有4名男生,2名女生,现从中选出4人参加校园植树活动,其中至少有一名女生的选法共有( )
A.8种 B.14种 C.12种 D.9种
8.收集一只棉铃虫的产卵数与温度的几组数据后发现两个变量有相关关系,按不同的曲线来拟合与之间的回归方程,并算出了对应的决定系数如下表:
拟合曲线 直线 指数曲线 抛物线 二次曲线
与的回归方程
0.746 0.996 0.902 0.002
则这组数据模型的回归方程的最好选择应是( )
A. B.
C. D.
9.若,则( )
A.-1 B.1 C.15 D.16
10.函数的图象大致是( )
A. B.
C. D.
11.函数,当时,有恒成立,则实数的取值范围是( )
A. B. C. D.
12.已知函数,其导函数记为,则( )
A.-3 B.3 C.2 D.-2
二 填空题(本大题共4小题,共20.0分)
13.复数的共轭复数为__________.
14.的展开式的第6项系数是__________.
15.已知甲,乙,丙三个人中,只有一个人会中国象棋.甲说:“我会”;乙说:“我不会”;丙说:“甲不会”.如果这三句话只有一句是真的,那么甲,乙,丙三个人中会中国象棋的是__________.
16.已知为实数,不等式恒成立,则的最小值为__________.
三 解答题(本大题共6小题,共70.0分.解答应写出文字说明,证明过程或演算步骤)
17.(本小题10.0分)在平面直角坐标系中,曲线所对应的图形经过伸缩变换得到图形.
(1)写出曲线的平面直角坐标方程;
(2)点在曲线上,求点到直线的距离的最小值及此时点的坐标.
18.(本小题12.0分)已知函数在处取得极大值1.
(1)求的值;
(2)当时,求的最大值.
19.(本小题12.0分)随着2022年北京冬季奥运会的如火如茶地进行.2022年北京冬季奥运会吉祥物“冰墩墩”受到人们的青睐,现某特许商品专卖店每天均进货一次,卖一个吉祥物“冰墩墩”可获利50元,若供大于求,则每天剩余的吉祥物“冰墩墩”需交保管费10元/个;若供不应求,则可从其他商店调剂供应,此时调剂的每一个吉祥物“冰墩墩”该店仅获利20元.该店调查上届冬季奥运会吉祥物每天(共计20天)的需求量(单位:个),统计数据得到下表:
每天需求量 162 163 164 165 166
频数 2 4 6 5 3
以上述20天吉祥物的需求量的频率作为各需求量发生的概率.记表示每天吉祥物“冰墩墩”的需求量.
(1)求的分布列;
(2)若该店某一天购进164个吉祥物“冰墩墩”,则当天的平均利润为多少元.
20.(本小题12.0分)
光伏发电是利用太阳能电池及相关设备将太阳光能直接转化为电能.近几年在国内出台的光伏发电补贴政策的引导下,某地光伏发电装机量急剧上涨,如下表:
年份 2011年 2012年 2013年 2014年 2015年 2016年 2017年 2018年
年份代码 1 2 3 4 5 6 7 8
新增光伏装机 量y兆瓦 0.4 0.8 1.6 3.1 5.1 7.1 9.7 12.2
某位同学分别用两种模型:①,②进行拟合,得到相应的回归方程并进行残差分析,残差图如下(注:残差等于)
经过计算得,,其中.
(1)根据残差图,比较模型①,②的拟合效果,应该选择哪个模型?并简要说明理由.
(2)根据(1)的判断结果及表中数据建立关于的回归方程,并预测该地区2020年新增光伏装机量是多少.(在计算回归系数时精确到0.01)
附:回归直线的斜率和截距的最小二乘估计公式分别为:.
21.(本小题12.0分)
已知函数.
(1)讨论函数的单调性;
(2)①若恒成立,求实数的取值集合;
②证明:.
22.(本小题10.0分)
在极坐标系中,点的极坐标是,曲线的极坐标方程为,以极点为坐标原点,极轴为轴的正半轴建立平面直角坐标系,斜率为-1的直线经过点.
(1)写出直线的参数方程和曲线的直角坐标方程;
(2)若直线和曲线相交于两点,求的值.
答案和解析
1.【答案】B
【解析】解:集合,则.
2.【答案】A
【解析】解:.
则复数在复平面内表示的点的坐标为.
3.【答案】D
解:根据题意,函数,
则,
则,
4.【答案】D
解:圆即,
即,即,
表示以为圆心,半径等于1的圆.
而点的极坐标为,
5.【答案】A
解:函数是奇函数,且在定义域内是增函数,正确;
函数在定义域内不具有单调性,错误;
函数在定义域内不具有单调性,错误;
函数的定义域是,不具有奇偶性,错误;
综上,应选.
6.【答案】C
【解析】解:模拟程序的运行,可得
执行循环体,
不满足条件,执行循环体,
不满足条件,执行循环体,
满足条件,退出循环,输出的值为15.
故选:.
7.【答案】B
【解析】
【分析】采用采用间接法,任意选有种,都是男生有1种,进而可得结果.
【详解】任意选有种,都是男生有1种,则至少有一名女生有14种.
故本题选.
8.【答案】B
【解析】由决定系数来刻画回归效果,的值越大越接近1,说明模型的拟合效果最好.故选:.
9.【答案】C
【解析】
【分析】利用赋值法结合条件即得.
【详解】因为,
令得,,
令得,,
所以,.
故选:C.
10.【答案】D
解:当时,,
即时,函数单调递减,当,函数单调递增,
又因为函数为偶函数,故排除,
故选:.
11.【答案】D
解:因为,
所以,
令得或,
可知函数在上单调递减,在上单调递增,在上单调递减,
而,
所以函数在上的最小值为-33,
因为当时,恒成立,
只需,
即,即,
解得.
故选.
12.【答案】C
【解析】
【分析】利用求导法则求出,即可知道,再利用,即可求解.
【详解】由已知得,
则,
则,
即,
则
,
故选:C.
13.【答案】
【解析】解:复数,
其共轭复数为.
14.【答案】-252
【解析】
【分析】应用二项式定理写出第6项系数.
【详解】由,
所以,第6项为,则,
故第6项系数是-252.
故答案为:-252
15.【答案】乙
【解析】解:假设甲会,那么甲 乙说的都是真话,与题意不符,所以甲不会;
假设乙会,那么甲 乙说的都是假话,丙说的真话,符合题意;
假设丙会,那么乙 丙说的都是真话,与题意不符,所以丙不会.
综上可得:会中国象棋的是乙,
16.【答案】-1
【解析】
【分析】先由恒成立得出,进而,
构造函数求解.
【详解】设,则不等式恒成立等价于成立,
显然当时不符合题意.当时,,
当时,,当时,,则在上单调递增,在上单调递减,
.由得.
令,则,当时,在上单调递减,
当时,在上单调递增,,
,则,此时.
故答案为:-1.
17.【答案】解:(1)由得到,代入到中,得.
即为曲线的直角坐标方程;
(2)设,则点到直线的距离为
,
其中,
当时,即,
于是,
同理,此时,即距离最小值为,此时点.
18.【答案】解:(1)已知函数在处取得极大值1,
,且函数在处有极值1,
,
解得
又当时,,
在和上单调递增,在单调递减,
故在处取得极大值,满足题意;
综上,;
(2)当时,,则,
当变化时,与的变化情况如下表:
-1 1
- 0 +
1 单调递减 极小值 单调递增 5
所以时,的最大值为5.
19.【答案】解:(1)可取,
,
,
所以分布列为:
162 163 164 165 166
(2)设表示每天的利润,
当时,,
当时,,
当时,,
当时,,
当时,,
所以平均利润为(元).
20.【答案】解:(1)选择模型①,理由如下:
根据残差图可以看出,模型①残差对应点分布在以横轴为对称轴,宽度小于1的水平带状区域内,模型①的各项残差的绝对值要远远小于模型②的各项残差的绝对值,所以模型①的拟合效果相对较好.
(2)由(1)知,关于的回归方程为,令,则.
由所给数据可得,
,
则,
.
所以关于的回归方程为.
预测该地区2020年新增光伏装机量为(兆瓦).
21.【答案】解:(1)因为,所以,
①当时,,函数在区间上单调递增;
②当时,令,令,
所以在上单调递减,在上单调递增.
(2)①由(1)可得当,函数在区间上单调递增,
又,所以,则,与条件矛盾,
当时,在上单调递减,在上单调递增,
所以,由已知,
所以,
设,则,
所以当时,,函数单调递增,
时,,函数单调递减,
又,
所以不等式的解集为.
②证明:设,
则,
当时,,函数单调递减,
时,,函数单调递增,
又,
所以,当且仅当时取等号,
由(1),当且仅当时取等号,
所以.
22.【答案】解:(1)点的直角坐标是,直线的倾斜角是,
直线的参数方程为,(为参数),
由直角坐标与极坐标互化公式得曲线的直角坐标方程为.
(2)将代入,得,
设对应参数分别为,则,
根据直线参数方程的几何意义得:
.
数学(理科)试卷
一 单选题(本大题共12小题,共60.0分.在每小题列出的选项中,选出符合题目的一项)
1.已知集合,则( )
A. B. C. D.
2.复数在复平面内表示的点的坐标为( )
A. B. C. D.
3.函数,则( )
A.-1 B.0 C. D.2
4.在极坐标系中,圆的圆心的极坐标是( )
A. B. C. D.
5.下列函数中,在定义域内既是奇函数又是增函数的是( )
A. B.
C. D.
6.执行如图所示的程序框图,输出的结果是( )
A.13 B.14 C.15 D.17
7.树立劳动观念对人的健康成长至关重要,某实践小组共有4名男生,2名女生,现从中选出4人参加校园植树活动,其中至少有一名女生的选法共有( )
A.8种 B.14种 C.12种 D.9种
8.收集一只棉铃虫的产卵数与温度的几组数据后发现两个变量有相关关系,按不同的曲线来拟合与之间的回归方程,并算出了对应的决定系数如下表:
拟合曲线 直线 指数曲线 抛物线 二次曲线
与的回归方程
0.746 0.996 0.902 0.002
则这组数据模型的回归方程的最好选择应是( )
A. B.
C. D.
9.若,则( )
A.-1 B.1 C.15 D.16
10.函数的图象大致是( )
A. B.
C. D.
11.函数,当时,有恒成立,则实数的取值范围是( )
A. B. C. D.
12.已知函数,其导函数记为,则( )
A.-3 B.3 C.2 D.-2
二 填空题(本大题共4小题,共20.0分)
13.复数的共轭复数为__________.
14.的展开式的第6项系数是__________.
15.已知甲,乙,丙三个人中,只有一个人会中国象棋.甲说:“我会”;乙说:“我不会”;丙说:“甲不会”.如果这三句话只有一句是真的,那么甲,乙,丙三个人中会中国象棋的是__________.
16.已知为实数,不等式恒成立,则的最小值为__________.
三 解答题(本大题共6小题,共70.0分.解答应写出文字说明,证明过程或演算步骤)
17.(本小题10.0分)在平面直角坐标系中,曲线所对应的图形经过伸缩变换得到图形.
(1)写出曲线的平面直角坐标方程;
(2)点在曲线上,求点到直线的距离的最小值及此时点的坐标.
18.(本小题12.0分)已知函数在处取得极大值1.
(1)求的值;
(2)当时,求的最大值.
19.(本小题12.0分)随着2022年北京冬季奥运会的如火如茶地进行.2022年北京冬季奥运会吉祥物“冰墩墩”受到人们的青睐,现某特许商品专卖店每天均进货一次,卖一个吉祥物“冰墩墩”可获利50元,若供大于求,则每天剩余的吉祥物“冰墩墩”需交保管费10元/个;若供不应求,则可从其他商店调剂供应,此时调剂的每一个吉祥物“冰墩墩”该店仅获利20元.该店调查上届冬季奥运会吉祥物每天(共计20天)的需求量(单位:个),统计数据得到下表:
每天需求量 162 163 164 165 166
频数 2 4 6 5 3
以上述20天吉祥物的需求量的频率作为各需求量发生的概率.记表示每天吉祥物“冰墩墩”的需求量.
(1)求的分布列;
(2)若该店某一天购进164个吉祥物“冰墩墩”,则当天的平均利润为多少元.
20.(本小题12.0分)
光伏发电是利用太阳能电池及相关设备将太阳光能直接转化为电能.近几年在国内出台的光伏发电补贴政策的引导下,某地光伏发电装机量急剧上涨,如下表:
年份 2011年 2012年 2013年 2014年 2015年 2016年 2017年 2018年
年份代码 1 2 3 4 5 6 7 8
新增光伏装机 量y兆瓦 0.4 0.8 1.6 3.1 5.1 7.1 9.7 12.2
某位同学分别用两种模型:①,②进行拟合,得到相应的回归方程并进行残差分析,残差图如下(注:残差等于)
经过计算得,,其中.
(1)根据残差图,比较模型①,②的拟合效果,应该选择哪个模型?并简要说明理由.
(2)根据(1)的判断结果及表中数据建立关于的回归方程,并预测该地区2020年新增光伏装机量是多少.(在计算回归系数时精确到0.01)
附:回归直线的斜率和截距的最小二乘估计公式分别为:.
21.(本小题12.0分)
已知函数.
(1)讨论函数的单调性;
(2)①若恒成立,求实数的取值集合;
②证明:.
22.(本小题10.0分)
在极坐标系中,点的极坐标是,曲线的极坐标方程为,以极点为坐标原点,极轴为轴的正半轴建立平面直角坐标系,斜率为-1的直线经过点.
(1)写出直线的参数方程和曲线的直角坐标方程;
(2)若直线和曲线相交于两点,求的值.
答案和解析
1.【答案】B
【解析】解:集合,则.
2.【答案】A
【解析】解:.
则复数在复平面内表示的点的坐标为.
3.【答案】D
解:根据题意,函数,
则,
则,
4.【答案】D
解:圆即,
即,即,
表示以为圆心,半径等于1的圆.
而点的极坐标为,
5.【答案】A
解:函数是奇函数,且在定义域内是增函数,正确;
函数在定义域内不具有单调性,错误;
函数在定义域内不具有单调性,错误;
函数的定义域是,不具有奇偶性,错误;
综上,应选.
6.【答案】C
【解析】解:模拟程序的运行,可得
执行循环体,
不满足条件,执行循环体,
不满足条件,执行循环体,
满足条件,退出循环,输出的值为15.
故选:.
7.【答案】B
【解析】
【分析】采用采用间接法,任意选有种,都是男生有1种,进而可得结果.
【详解】任意选有种,都是男生有1种,则至少有一名女生有14种.
故本题选.
8.【答案】B
【解析】由决定系数来刻画回归效果,的值越大越接近1,说明模型的拟合效果最好.故选:.
9.【答案】C
【解析】
【分析】利用赋值法结合条件即得.
【详解】因为,
令得,,
令得,,
所以,.
故选:C.
10.【答案】D
解:当时,,
即时,函数单调递减,当,函数单调递增,
又因为函数为偶函数,故排除,
故选:.
11.【答案】D
解:因为,
所以,
令得或,
可知函数在上单调递减,在上单调递增,在上单调递减,
而,
所以函数在上的最小值为-33,
因为当时,恒成立,
只需,
即,即,
解得.
故选.
12.【答案】C
【解析】
【分析】利用求导法则求出,即可知道,再利用,即可求解.
【详解】由已知得,
则,
则,
即,
则
,
故选:C.
13.【答案】
【解析】解:复数,
其共轭复数为.
14.【答案】-252
【解析】
【分析】应用二项式定理写出第6项系数.
【详解】由,
所以,第6项为,则,
故第6项系数是-252.
故答案为:-252
15.【答案】乙
【解析】解:假设甲会,那么甲 乙说的都是真话,与题意不符,所以甲不会;
假设乙会,那么甲 乙说的都是假话,丙说的真话,符合题意;
假设丙会,那么乙 丙说的都是真话,与题意不符,所以丙不会.
综上可得:会中国象棋的是乙,
16.【答案】-1
【解析】
【分析】先由恒成立得出,进而,
构造函数求解.
【详解】设,则不等式恒成立等价于成立,
显然当时不符合题意.当时,,
当时,,当时,,则在上单调递增,在上单调递减,
.由得.
令,则,当时,在上单调递减,
当时,在上单调递增,,
,则,此时.
故答案为:-1.
17.【答案】解:(1)由得到,代入到中,得.
即为曲线的直角坐标方程;
(2)设,则点到直线的距离为
,
其中,
当时,即,
于是,
同理,此时,即距离最小值为,此时点.
18.【答案】解:(1)已知函数在处取得极大值1,
,且函数在处有极值1,
,
解得
又当时,,
在和上单调递增,在单调递减,
故在处取得极大值,满足题意;
综上,;
(2)当时,,则,
当变化时,与的变化情况如下表:
-1 1
- 0 +
1 单调递减 极小值 单调递增 5
所以时,的最大值为5.
19.【答案】解:(1)可取,
,
,
所以分布列为:
162 163 164 165 166
(2)设表示每天的利润,
当时,,
当时,,
当时,,
当时,,
当时,,
所以平均利润为(元).
20.【答案】解:(1)选择模型①,理由如下:
根据残差图可以看出,模型①残差对应点分布在以横轴为对称轴,宽度小于1的水平带状区域内,模型①的各项残差的绝对值要远远小于模型②的各项残差的绝对值,所以模型①的拟合效果相对较好.
(2)由(1)知,关于的回归方程为,令,则.
由所给数据可得,
,
则,
.
所以关于的回归方程为.
预测该地区2020年新增光伏装机量为(兆瓦).
21.【答案】解:(1)因为,所以,
①当时,,函数在区间上单调递增;
②当时,令,令,
所以在上单调递减,在上单调递增.
(2)①由(1)可得当,函数在区间上单调递增,
又,所以,则,与条件矛盾,
当时,在上单调递减,在上单调递增,
所以,由已知,
所以,
设,则,
所以当时,,函数单调递增,
时,,函数单调递减,
又,
所以不等式的解集为.
②证明:设,
则,
当时,,函数单调递减,
时,,函数单调递增,
又,
所以,当且仅当时取等号,
由(1),当且仅当时取等号,
所以.
22.【答案】解:(1)点的直角坐标是,直线的倾斜角是,
直线的参数方程为,(为参数),
由直角坐标与极坐标互化公式得曲线的直角坐标方程为.
(2)将代入,得,
设对应参数分别为,则,
根据直线参数方程的几何意义得:
.
同课章节目录
