第十章 数据的收集、整理与描述 单元同步检测试题(含答案)
文档属性
| 名称 | 第十章 数据的收集、整理与描述 单元同步检测试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 284.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-27 09:26:56 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第十章《数据的收集、整理与描述》单元检测题
题号 一 二 三 总分
21 22 23 24 25 26 27 28
分数
一、选择题(本大题共10小题,每小题3分,共计30分)
为了了解一批电视机的寿命,从中抽取100台电视机进行试验,这个问题的样本是( )
A.这批电视机 B.这批电视机的寿命
C.抽取的100台电视机的寿命 D.100
为了了解某市七年级8000人的身高情况,从中抽取800名学生的身高进行统计,下列说法不正确的是( )
A.8000人的身高情况是总体
B.每个学生的身高是个体
C.800名学生身高情况是一个样本
D.样本容量为8000人
一个班有40名学生,在期末体育考核中,优秀的有18人,在扇形统计图中,代表体育优秀扇形的圆心角是( )
A.144° B.162° C.216° D.250°
4.一组数据:10,8,6,10,8,13,11,10,12,7,10,11,10,9,12,10,9,12,9,8,那么频率为0.3的范围是( )
A.6~7 B.8~9 C.10~11 D.12~13
5.如图是九(1)班45名同学每周课外阅读时间的频数直方图(每组含前一个边界值,不含后一个边界值).由图可知,人数最多的一组是( )
A.2~4小时 B.4~6小时 C.6~8小时 D.8~10小时
6.如图是某商厦某个月甲、乙、丙三种品牌彩电的销售量统计图,则甲、丙两种品牌的彩电该月的销售量之和为( )
A.50台 B.65台 C.85台 D.95台
7.某市近几年干旱,市政府采取各种措施扩大水源,措施之一是建水厂.如图是该市目前水源结构的扇形图,根据图中圆心角的大小计算出黄河水在总供水中所占的百分比为( )
A.64% B.60% C.54% D.24%
8.为了了解天鹅湖校区2019-2020学年1600名七年级学生的体重情况,从中抽取了100名学生的体重,就这个问题,下面说法正确的是( )
A.1600名学生的体重是总体 B.1600名学生是总体
C.每个学生是个体 D.100名学生是所抽取的一个样本
9.要反映我县某初中七年级学生期末考试数学成绩的分布情况(按照分数段描述),宜采用( )
A.条形统计图 B.扇形统计图
C.折线统计图 D.频数分布直方图
10.某池塘中放养了鲫鱼 1000 条,鲮鱼若干条,在几次随机捕捞中,共抓到鲫鱼 200 条, 鲮鱼 400 条,估计池塘中原来放养了鲮鱼( )
A.500 条 B.1000 条 C.2000 条 D.3000 条
二、填空题(本大题共8小题,每小题3分,共24分)
11.为了调查学生考试成绩情况,从班中抽取总分前十名学生,这种抽样调查 (“适合”或“不适合”).
12.某校为了了解300名七年级学生的视力情况,从中抽取50名学生进行测试,其中总体为 ,样本为 .
13.在抽取样本的过程中,使总体中的每一个个体都有相等的机会被抽到,这样的抽样方法是一种 的随机抽样.
14.如果某地青少年、成年人、老年人的人口比为2:4:4.现要抽取一个样本容量为1000的样本,青少年人数为 人,成年人人数为 人.
15.在拆线统计图上点的位置 ,则数据越大,它反映的是数据波动情况,条形统计图上的 越高,则相应的数据越大,直方图运用长方形的 表示频数.
16.已知数据为100个,最大值为89,最小值为40,组距为8,则可分成组数为 组.
17.已知60个数分别落在5个组内,第一,二,三,四,五组数据的个数分别是12,8,x,20,5,则第三组的频数为 .
18.对某班学生一次数学测试成绩进行统计如图所示,该班人数为 人,70.5~80.5范围人数占全班 %.如果以80.5以上为优良,那么优良率为 (分数为整数).
三、解答题(本大题共46分,19题6分,20---24题每题8分)
19.下面这几个抽样调查选取样本的方法是否合适?并说明理由.
(1)为调查全校学生对购买正版书籍、唱片和软件的支持率,在全校所有的班级中任意抽取8个班级,调查这8个班所有学生对购买正版书籍、唱片和软件的支持率;
(2)为调查一个省的环境污染情况,调查省会城市的环境污染情况.
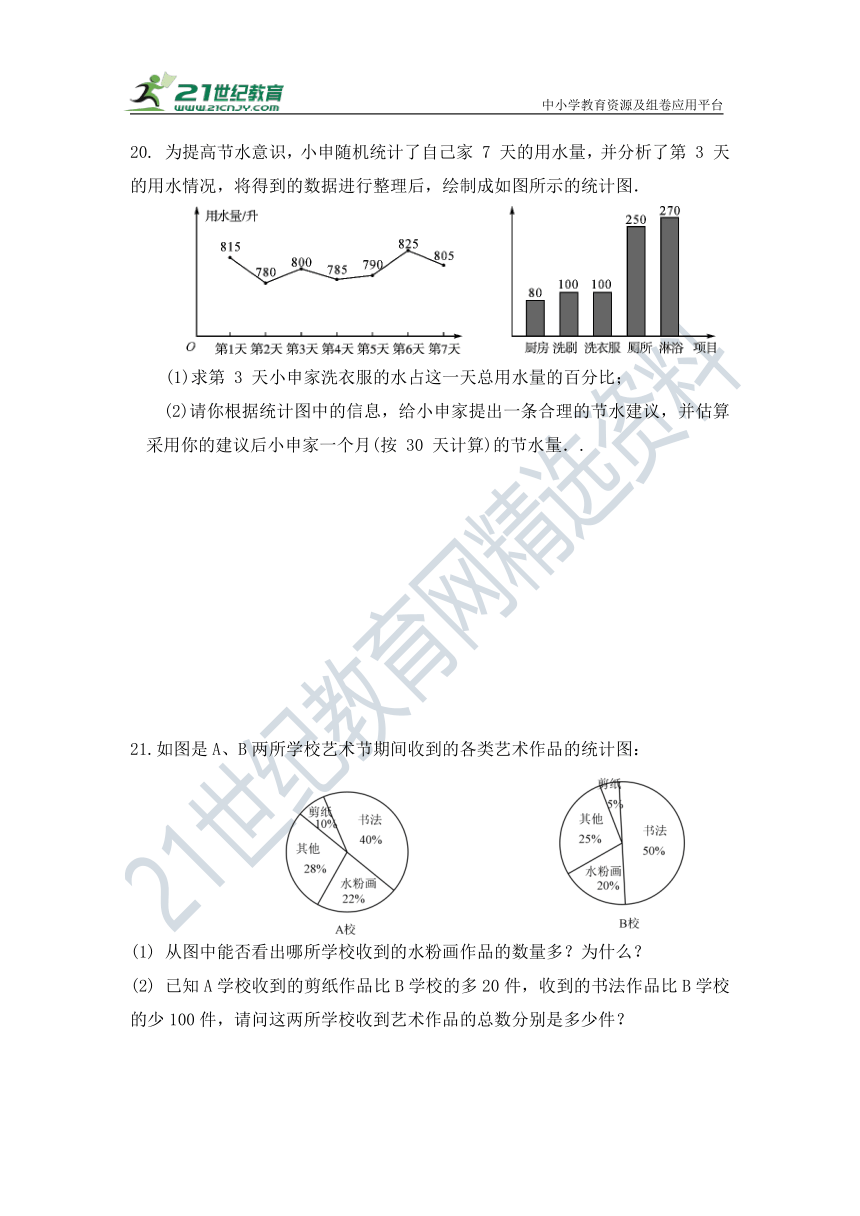
20. 为提高节水意识,小申随机统计了自己家 7 天的用水量,并分析了第 3 天的用水情况,将得到的数据进行整理后,绘制成如图所示的统计图.
(1)求第 3 天小申家洗衣服的水占这一天总用水量的百分比;
(2)请你根据统计图中的信息,给小申家提出一条合理的节水建议,并估算采用你的建议后小申家一个月(按 30 天计算)的节水量..
21.如图是A、B两所学校艺术节期间收到的各类艺术作品的统计图:
(1) 从图中能否看出哪所学校收到的水粉画作品的数量多?为什么?
(2) 已知A学校收到的剪纸作品比B学校的多20件,收到的书法作品比B学校的少100件,请问这两所学校收到艺术作品的总数分别是多少件?
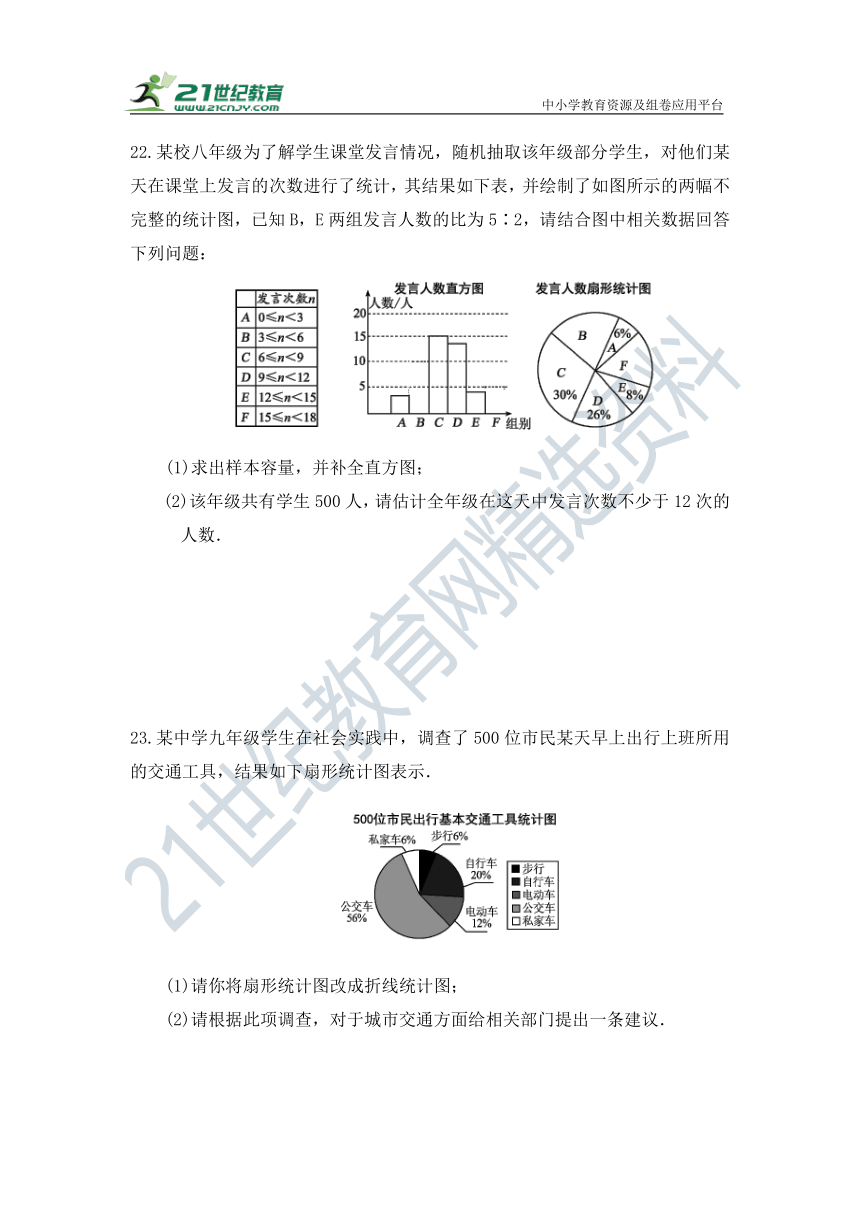
22.某校八年级为了解学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如下表,并绘制了如图所示的两幅不完整的统计图,已知B,E两组发言人数的比为5∶2,请结合图中相关数据回答下列问题:
(1)求出样本容量,并补全直方图;
(2)该年级共有学生500人,请估计全年级在这天中发言次数不少于12次的人数.
23.某中学九年级学生在社会实践中,调查了500位市民某天早上出行上班所用的交通工具,结果如下扇形统计图表示.
(1)请你将扇形统计图改成折线统计图;
(2)请根据此项调查,对于城市交通方面给相关部门提出一条建议.
24. 某校为了解“阳光体育”活动的开展情况,从全校2000名学生中,随机抽取部分学生进行问卷调查(每名学生只能填写一项自己喜欢的活动项目),并将调查结果绘制成如下两幅不完整的统计图.
根据以上信息,解答下列问题:
(1)被调查的学生共有 人,并补全条形统计图;
(2)在扇形统计图中,m= ,n= ,表示区域C的圆心角为 度;
(3)全校学生中喜欢篮球的人数大约有 。
参考答案:
一.填空题
题号 1 2 3 4 5 6 7 8 9 10
答案 C D B B B D A A D C
二.选择题
11.为了调查学生考试成绩情况,从班中抽取总分前十名学生,这种抽样调查 不适合 (“适合”或“不适合”).
【考点】抽样调查的可靠性.
【分析】抽取样本注意事项就是要考虑样本具有广泛性与代表性,所谓代表性,就是抽取的样本必须是随机的,即各个方面,各个层次的对象都要有所体现.
【解答】解:为了调查学生考试成绩情况,从班中抽取总分前十名学生,样本不具有广泛性与代表性,这种抽样调查不适合.
故答案为:不适合.
【点评】考查了抽样调查的可靠性,样本具有代表性是指抽取的样本必须是随机的,即各个方面,各个层次的对象都要有所体现.
12.某校为了了解300名七年级学生的视力情况,从中抽取50名学生进行测试,其中总体为 某校300名七年级学生的视力情况 ,样本为 从中抽的取50名学生的视力情况 .
【考点】总体、个体、样本、样本容量.
【分析】总体是指考查的对象的全体,个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分个体.我们在区分总体、个体、样本、样本容量,这四个概念时,首先找出考查的对象.
【解答】解:总体是:某校300名七年级学生的视力情况;
样本是:从中抽的取50名学生的视力情况.
故答案是:
【点评】考查了总体、个体、样本、样本容量,解题要分清具体问题中的总体、个体与样本,关键是明确考查的对象.总体、个体与样本的考查对象是相同的,所不同的是范围的大小.
13.在抽取样本的过程中,使总体中的每一个个体都有相等的机会被抽到,这样的抽样方法是一种 简单 的随机抽样.
【考点】全面调查与抽样调查.
【分析】根据简单随机抽样的定义即可解答.
【解答】解:在抽取样本的过程中,使总体中的每一个个体都有相等的机会被抽到,这样的抽样方法是一种简单的随机抽样.
故答案是:简单.
【点评】本题考查了简单随机抽样的定义,记忆定义是关键.
14.如果某地青少年、成年人、老年人的人口比为2:4:4.现要抽取一个样本容量为1000的样本,青少年人数为 200 人,成年人人数为 400 人.
【考点】总体、个体、样本、样本容量.
【专题】计算题.
【分析】总人数乘以对应的比例即可求解.
【解答】解:青少年人数为1000×=200(人);
成年人人数是:10000×=400(人).
故答案是:200;400.
【点评】本题考查了样本和样本容量,正确理解每类人所占的比例是关键.
15.在拆线统计图上点的位置 高 ,则数据越大,它反映的是数据波动情况,条形统计图上的 长度 越高,则相应的数据越大,直方图运用长方形的 长 表示频数.
【考点】统计图的选择.
【分析】根据常用的几种统计图反映数据的不同特征结合实际来求解.
【解答】解:在拆线统计图上点的位置 高,则数据越大,它反映的是数据波动情况,条形统计图上的 长度越高,则相应的数据越大,直方图运用长方形的 长表示频数.
故答案为:高,长度,长.
【点评】此题根据折线统计图、条形统计图和直方图各自的特点来求解.
16.已知数据为100个,最大值为89,最小值为40,组距为8,则可分成组数为 7 组.
【考点】频数(率)分布表.
【分析】根据组数=(最大值﹣最小值)÷组距计算,注意小数部分要进位.
【解答】解:最大值为89,最小值为40,它们的差是89﹣40=49,
已知组距为8,那么由于≈7;
则可分成组数为7组.
故答案为:7.
【点评】本题考查的是频数(率)分布表中组数的计算,属于基础题,只要根据组数的定义“数据分成的组的个数称为组数”来解即可.
17.已知60个数分别落在5个组内,第一,二,三,四,五组数据的个数分别是12,8,x,20,5,则第三组的频数为 15 .
【考点】频数与频率.
【分析】根据共有60个数据,求出第三组的频数即可.
【解答】解:第三组的频数为:60﹣12﹣8﹣20﹣5=15.
故答案为:15.
【点评】本题考查了频数和频率,注意频数是指每个对象出现的次数.
18.对某班学生一次数学测试成绩进行统计如图所示,该班人数为 50 人,70.5~80.5范围人数占全班 30 %.如果以80.5以上为优良,那么优良率为 40% (分数为整数).
【考点】频数(率)分布直方图.
【专题】图表型.
【分析】此班人数就是把每一个条的频数加起来即可;
根据频数分布直方图可得70.5~80.5范围人数有15人,再用15÷50×100%可得答案;
首先利用频数分布直方图可得80.5以上范围人数,再算出百分比即可.
【解答】解:该班人数:5+10+15+12+8=50(人),
70.5~80.5范围人数所占百分比:×100%=30%;
优良率:(12+8)÷50=40%,
故答案为:50;30%;40%.
【点评】本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
三.解答题
19. 解:(1)选取样本方法合适,具有代表性.
(2)选取样本方法不合适,样本缺乏代表性.;
20. 解:(1) ×100%=12.5% .
(2)答案不唯一.例如:可以用洗衣服的水冲厕所.采用该建议,每天大约可以节约用水 100 升,一个月估计可以节约用水 100×30=3 000 升.
21.⑴.不能.因为在只知道各校水粉画作品的百分比而不知道总量的前提下,是不能进行比较的.
⑵设A、B两所学校收到艺术作品的总数分别是x件和y件则解之: 答略.
22. 解:(1)由题意得,E组为(10÷5)×2=4(人),发言人总数为4÷8%=50(人),A组为50×6%=3(人),C组为50×30%=15(人),D组为50×26%=13(人),∴F组为50-3-10-15-13-4=5(人),补全直方图略.
(2)∵在统计的50人中,发言次数不少于12次的有4+5=9(人),∴在这天发言次数不少于12次的频率为=18%,∴全年级500人中,在这天里发言次数不少于12次的人数为500×18%=90(人).
23. 解:(1)步行人数为500×6%=30(人);自行车人数为500×20%=100(人);
电动车人数为500×12%=60(人);公交车人数为500×56%=280(人);私家车人数为500×6%=30(人),改成折线统计图略.
(2)答案不唯一,略.
24. 解:(1)100。条形统计图为:
(2)30;10;144°。
(3)∵全校共有2000人,喜欢篮球的占10%,
∴喜欢篮球的有2000×10%=200人。
第十章《数据的收集、整理与描述》单元检测题
题号 一 二 三 总分
21 22 23 24 25 26 27 28
分数
一、选择题(本大题共10小题,每小题3分,共计30分)
为了了解一批电视机的寿命,从中抽取100台电视机进行试验,这个问题的样本是( )
A.这批电视机 B.这批电视机的寿命
C.抽取的100台电视机的寿命 D.100
为了了解某市七年级8000人的身高情况,从中抽取800名学生的身高进行统计,下列说法不正确的是( )
A.8000人的身高情况是总体
B.每个学生的身高是个体
C.800名学生身高情况是一个样本
D.样本容量为8000人
一个班有40名学生,在期末体育考核中,优秀的有18人,在扇形统计图中,代表体育优秀扇形的圆心角是( )
A.144° B.162° C.216° D.250°
4.一组数据:10,8,6,10,8,13,11,10,12,7,10,11,10,9,12,10,9,12,9,8,那么频率为0.3的范围是( )
A.6~7 B.8~9 C.10~11 D.12~13
5.如图是九(1)班45名同学每周课外阅读时间的频数直方图(每组含前一个边界值,不含后一个边界值).由图可知,人数最多的一组是( )
A.2~4小时 B.4~6小时 C.6~8小时 D.8~10小时
6.如图是某商厦某个月甲、乙、丙三种品牌彩电的销售量统计图,则甲、丙两种品牌的彩电该月的销售量之和为( )
A.50台 B.65台 C.85台 D.95台
7.某市近几年干旱,市政府采取各种措施扩大水源,措施之一是建水厂.如图是该市目前水源结构的扇形图,根据图中圆心角的大小计算出黄河水在总供水中所占的百分比为( )
A.64% B.60% C.54% D.24%
8.为了了解天鹅湖校区2019-2020学年1600名七年级学生的体重情况,从中抽取了100名学生的体重,就这个问题,下面说法正确的是( )
A.1600名学生的体重是总体 B.1600名学生是总体
C.每个学生是个体 D.100名学生是所抽取的一个样本
9.要反映我县某初中七年级学生期末考试数学成绩的分布情况(按照分数段描述),宜采用( )
A.条形统计图 B.扇形统计图
C.折线统计图 D.频数分布直方图
10.某池塘中放养了鲫鱼 1000 条,鲮鱼若干条,在几次随机捕捞中,共抓到鲫鱼 200 条, 鲮鱼 400 条,估计池塘中原来放养了鲮鱼( )
A.500 条 B.1000 条 C.2000 条 D.3000 条
二、填空题(本大题共8小题,每小题3分,共24分)
11.为了调查学生考试成绩情况,从班中抽取总分前十名学生,这种抽样调查 (“适合”或“不适合”).
12.某校为了了解300名七年级学生的视力情况,从中抽取50名学生进行测试,其中总体为 ,样本为 .
13.在抽取样本的过程中,使总体中的每一个个体都有相等的机会被抽到,这样的抽样方法是一种 的随机抽样.
14.如果某地青少年、成年人、老年人的人口比为2:4:4.现要抽取一个样本容量为1000的样本,青少年人数为 人,成年人人数为 人.
15.在拆线统计图上点的位置 ,则数据越大,它反映的是数据波动情况,条形统计图上的 越高,则相应的数据越大,直方图运用长方形的 表示频数.
16.已知数据为100个,最大值为89,最小值为40,组距为8,则可分成组数为 组.
17.已知60个数分别落在5个组内,第一,二,三,四,五组数据的个数分别是12,8,x,20,5,则第三组的频数为 .
18.对某班学生一次数学测试成绩进行统计如图所示,该班人数为 人,70.5~80.5范围人数占全班 %.如果以80.5以上为优良,那么优良率为 (分数为整数).
三、解答题(本大题共46分,19题6分,20---24题每题8分)
19.下面这几个抽样调查选取样本的方法是否合适?并说明理由.
(1)为调查全校学生对购买正版书籍、唱片和软件的支持率,在全校所有的班级中任意抽取8个班级,调查这8个班所有学生对购买正版书籍、唱片和软件的支持率;
(2)为调查一个省的环境污染情况,调查省会城市的环境污染情况.
20. 为提高节水意识,小申随机统计了自己家 7 天的用水量,并分析了第 3 天的用水情况,将得到的数据进行整理后,绘制成如图所示的统计图.
(1)求第 3 天小申家洗衣服的水占这一天总用水量的百分比;
(2)请你根据统计图中的信息,给小申家提出一条合理的节水建议,并估算采用你的建议后小申家一个月(按 30 天计算)的节水量..
21.如图是A、B两所学校艺术节期间收到的各类艺术作品的统计图:
(1) 从图中能否看出哪所学校收到的水粉画作品的数量多?为什么?
(2) 已知A学校收到的剪纸作品比B学校的多20件,收到的书法作品比B学校的少100件,请问这两所学校收到艺术作品的总数分别是多少件?
22.某校八年级为了解学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如下表,并绘制了如图所示的两幅不完整的统计图,已知B,E两组发言人数的比为5∶2,请结合图中相关数据回答下列问题:
(1)求出样本容量,并补全直方图;
(2)该年级共有学生500人,请估计全年级在这天中发言次数不少于12次的人数.
23.某中学九年级学生在社会实践中,调查了500位市民某天早上出行上班所用的交通工具,结果如下扇形统计图表示.
(1)请你将扇形统计图改成折线统计图;
(2)请根据此项调查,对于城市交通方面给相关部门提出一条建议.
24. 某校为了解“阳光体育”活动的开展情况,从全校2000名学生中,随机抽取部分学生进行问卷调查(每名学生只能填写一项自己喜欢的活动项目),并将调查结果绘制成如下两幅不完整的统计图.
根据以上信息,解答下列问题:
(1)被调查的学生共有 人,并补全条形统计图;
(2)在扇形统计图中,m= ,n= ,表示区域C的圆心角为 度;
(3)全校学生中喜欢篮球的人数大约有 。
参考答案:
一.填空题
题号 1 2 3 4 5 6 7 8 9 10
答案 C D B B B D A A D C
二.选择题
11.为了调查学生考试成绩情况,从班中抽取总分前十名学生,这种抽样调查 不适合 (“适合”或“不适合”).
【考点】抽样调查的可靠性.
【分析】抽取样本注意事项就是要考虑样本具有广泛性与代表性,所谓代表性,就是抽取的样本必须是随机的,即各个方面,各个层次的对象都要有所体现.
【解答】解:为了调查学生考试成绩情况,从班中抽取总分前十名学生,样本不具有广泛性与代表性,这种抽样调查不适合.
故答案为:不适合.
【点评】考查了抽样调查的可靠性,样本具有代表性是指抽取的样本必须是随机的,即各个方面,各个层次的对象都要有所体现.
12.某校为了了解300名七年级学生的视力情况,从中抽取50名学生进行测试,其中总体为 某校300名七年级学生的视力情况 ,样本为 从中抽的取50名学生的视力情况 .
【考点】总体、个体、样本、样本容量.
【分析】总体是指考查的对象的全体,个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分个体.我们在区分总体、个体、样本、样本容量,这四个概念时,首先找出考查的对象.
【解答】解:总体是:某校300名七年级学生的视力情况;
样本是:从中抽的取50名学生的视力情况.
故答案是:
【点评】考查了总体、个体、样本、样本容量,解题要分清具体问题中的总体、个体与样本,关键是明确考查的对象.总体、个体与样本的考查对象是相同的,所不同的是范围的大小.
13.在抽取样本的过程中,使总体中的每一个个体都有相等的机会被抽到,这样的抽样方法是一种 简单 的随机抽样.
【考点】全面调查与抽样调查.
【分析】根据简单随机抽样的定义即可解答.
【解答】解:在抽取样本的过程中,使总体中的每一个个体都有相等的机会被抽到,这样的抽样方法是一种简单的随机抽样.
故答案是:简单.
【点评】本题考查了简单随机抽样的定义,记忆定义是关键.
14.如果某地青少年、成年人、老年人的人口比为2:4:4.现要抽取一个样本容量为1000的样本,青少年人数为 200 人,成年人人数为 400 人.
【考点】总体、个体、样本、样本容量.
【专题】计算题.
【分析】总人数乘以对应的比例即可求解.
【解答】解:青少年人数为1000×=200(人);
成年人人数是:10000×=400(人).
故答案是:200;400.
【点评】本题考查了样本和样本容量,正确理解每类人所占的比例是关键.
15.在拆线统计图上点的位置 高 ,则数据越大,它反映的是数据波动情况,条形统计图上的 长度 越高,则相应的数据越大,直方图运用长方形的 长 表示频数.
【考点】统计图的选择.
【分析】根据常用的几种统计图反映数据的不同特征结合实际来求解.
【解答】解:在拆线统计图上点的位置 高,则数据越大,它反映的是数据波动情况,条形统计图上的 长度越高,则相应的数据越大,直方图运用长方形的 长表示频数.
故答案为:高,长度,长.
【点评】此题根据折线统计图、条形统计图和直方图各自的特点来求解.
16.已知数据为100个,最大值为89,最小值为40,组距为8,则可分成组数为 7 组.
【考点】频数(率)分布表.
【分析】根据组数=(最大值﹣最小值)÷组距计算,注意小数部分要进位.
【解答】解:最大值为89,最小值为40,它们的差是89﹣40=49,
已知组距为8,那么由于≈7;
则可分成组数为7组.
故答案为:7.
【点评】本题考查的是频数(率)分布表中组数的计算,属于基础题,只要根据组数的定义“数据分成的组的个数称为组数”来解即可.
17.已知60个数分别落在5个组内,第一,二,三,四,五组数据的个数分别是12,8,x,20,5,则第三组的频数为 15 .
【考点】频数与频率.
【分析】根据共有60个数据,求出第三组的频数即可.
【解答】解:第三组的频数为:60﹣12﹣8﹣20﹣5=15.
故答案为:15.
【点评】本题考查了频数和频率,注意频数是指每个对象出现的次数.
18.对某班学生一次数学测试成绩进行统计如图所示,该班人数为 50 人,70.5~80.5范围人数占全班 30 %.如果以80.5以上为优良,那么优良率为 40% (分数为整数).
【考点】频数(率)分布直方图.
【专题】图表型.
【分析】此班人数就是把每一个条的频数加起来即可;
根据频数分布直方图可得70.5~80.5范围人数有15人,再用15÷50×100%可得答案;
首先利用频数分布直方图可得80.5以上范围人数,再算出百分比即可.
【解答】解:该班人数:5+10+15+12+8=50(人),
70.5~80.5范围人数所占百分比:×100%=30%;
优良率:(12+8)÷50=40%,
故答案为:50;30%;40%.
【点评】本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
三.解答题
19. 解:(1)选取样本方法合适,具有代表性.
(2)选取样本方法不合适,样本缺乏代表性.;
20. 解:(1) ×100%=12.5% .
(2)答案不唯一.例如:可以用洗衣服的水冲厕所.采用该建议,每天大约可以节约用水 100 升,一个月估计可以节约用水 100×30=3 000 升.
21.⑴.不能.因为在只知道各校水粉画作品的百分比而不知道总量的前提下,是不能进行比较的.
⑵设A、B两所学校收到艺术作品的总数分别是x件和y件则解之: 答略.
22. 解:(1)由题意得,E组为(10÷5)×2=4(人),发言人总数为4÷8%=50(人),A组为50×6%=3(人),C组为50×30%=15(人),D组为50×26%=13(人),∴F组为50-3-10-15-13-4=5(人),补全直方图略.
(2)∵在统计的50人中,发言次数不少于12次的有4+5=9(人),∴在这天发言次数不少于12次的频率为=18%,∴全年级500人中,在这天里发言次数不少于12次的人数为500×18%=90(人).
23. 解:(1)步行人数为500×6%=30(人);自行车人数为500×20%=100(人);
电动车人数为500×12%=60(人);公交车人数为500×56%=280(人);私家车人数为500×6%=30(人),改成折线统计图略.
(2)答案不唯一,略.
24. 解:(1)100。条形统计图为:
(2)30;10;144°。
(3)∵全校共有2000人,喜欢篮球的占10%,
∴喜欢篮球的有2000×10%=200人。
