第二十章 数据的描述 单元同步检测试题(含答案)
文档属性
| 名称 | 第二十章 数据的描述 单元同步检测试题(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 521.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-27 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第二十章《数据的收集、整理与描述》单元检测题
题号 一 二 三 总分
19 20 21 22 23 24
分数
一、选择题(本大题共10小题,每小题3分,共计30分)
1. 九年级(1)班15名男同学进行引体向上测试,每人只测一次,测试结果统计如下:
引体向上数/个 0 1 2 3 4 5 6 7 8
人数 1 1 2 1 3 3 2 1 1
这15名男同学引体向上数的中位数是( )
A.2 B.3 C.4 D.5
2. 国产大飞机C919用数学建模的方法预测的价格是(单位:美元):5 098,5 099,5 001,5 002,4 990,4 920,5 080,5 010,4 901,4 902,这组数据的平均数是( )
A.5 000.3 B.4 999.7
C.4 997 D.5 003
3. 在光明中学组织的全校师生迎“五四”诗词大赛中,来自不同年级的25名参赛同学的得分情况如图所示.这些成绩的中位数和众数分别是( )
A.96分、98分 B. 97分、98分
C. 98分、96分 D. 97分、96分
4.一组数据:10,8,6,10,8,13,11,10,12,7,10,11,10,9,12,10,9,12,9,8,那么频率为0.3的范围是( )
A.6~7 B.8~9 C.10~11 D.12~13
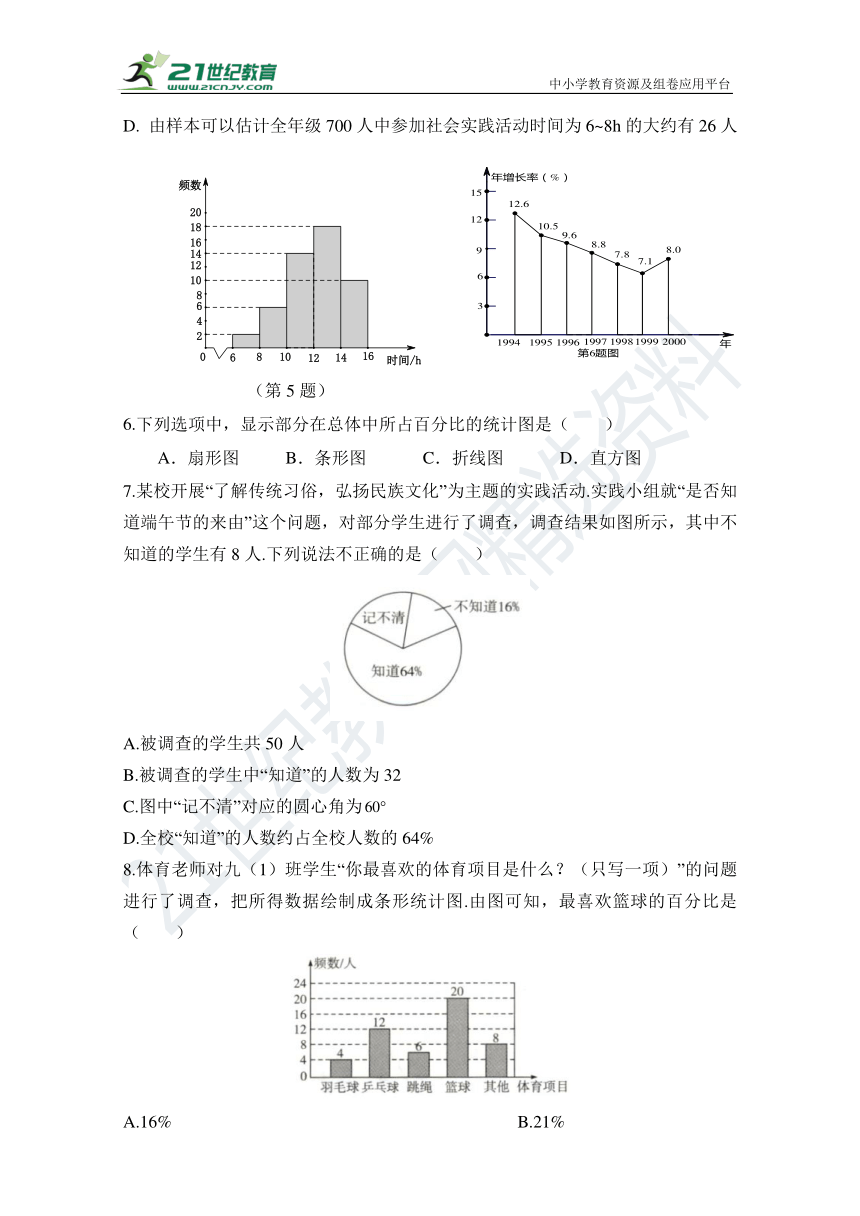
5.为了了解本校七年级700名学生上学期参加社会实践活动的时间,
随机对该年级50名学生进行了调查.根据收集的数据绘制了频数分
布直方图,则以下说法正确的是( )
A.学生参加社会实践活动时间最多为16h
B. 学生参加社会实践活动时间大多数是12~14h
C. 学生参加社会实践活动时间不少于10h的为84%
D. 由样本可以估计全年级700人中参加社会实践活动时间为6~8h的大约有26人
(第5题)
6.下列选项中,显示部分在总体中所占百分比的统计图是( )
A.扇形图 B.条形图 C.折线图 D.直方图
7.某校开展“了解传统习俗,弘扬民族文化”为主题的实践活动.实践小组就“是否知道端午节的来由”这个问题,对部分学生进行了调查,调查结果如图所示,其中不知道的学生有8人.下列说法不正确的是( )
A.被调查的学生共50人
B.被调查的学生中“知道”的人数为32
C.图中“记不清”对应的圆心角为
D.全校“知道”的人数约占全校人数的64%
8.体育老师对九(1)班学生“你最喜欢的体育项目是什么?(只写一项)”的问题进行了调查,把所得数据绘制成条形统计图.由图可知,最喜欢篮球的百分比是( )
A.16% B.21%
C.30% D.40%
9.女子排球队6名场上队员的身高(单位:cm)是:170,174,178,180,180,184.现用身高178cm的队员替换场上身高174cm的队员,与换人前相比,场上队员的身高( )
A.平均数变大,中位数不变
B.平均数变大,中位数变大
C.平均数变小,中位数不变
D.平均数变小,中位数变大
10.在一次体育测试中,小明记录了本班10名同学一分钟跳绳的成绩,如表:
成绩 150 160 170 180 190
人数 2 3 2 2 1
对于这10名学生的跳绳成绩,下列说法错误的是( )
A.众数是160 B.中位数是165
C.平均数是167 D.方差是104.5
二、填空题(本大题共8小题,每小题3分,共24分)
11.样本数据1,5,n,6,8的众数是1,则这组数的中位数是 .
12.某地教育局拟招聘一批数学教师,现有一名应聘者笔试成绩88分、面试成绩90分,综合成绩按照笔试占40%、面试占60%进行计算,该应聘者的综合成绩为 分.
13.一组数1、2、3、4、5的方差是S12与另一组数3、4、5、6、7的方差S22的大小比较S12 S22(填写:大于、等于、小于).
14.某次测验后,60~70分这组人数占全班总人数的20%,若全班有45人,则该组的频数为________.
15.对某中学同龄的70名女生的身高进行测量后,得到一组数据,其中最大值为169 cm,最小值为145 cm,对这组数据进行整理后,确定它的组距为2.3 cm,则组数为________.
16.如图是某农场里三种蔬菜种植面积的扇形统计图,若西红柿种植面积为4.2公顷,则这三种蔬菜种植总面积是________公顷,表示黄瓜的扇形圆心角的度数为________.
17、某校规定:学生的数学期未总计成须由卷面成绩、研究性学习成绩、平时成绩三部分构成,各部分所占比例如图所示.小明本学期数学学科的卷面成绩、研究性学习成绩、平时成绩得分依次为分、分、分,则小明的数学期末总评成绩为________分.
18、“学习强国”是王老师每天的必修课,下表是王老师一周的学习得分情况:
日期 11.1 11.2 11.3 11.4 11.5 11.6 11.7
得分 49 60 48 42 55 55 55
则这组数据的众数为______.
三、解答题(本大题共46分,19题6分,20---24题每题8分)
19、少年学生走近操场,走到阳关下,积极参加体育锻炼,我国启动了“全国亿万学生阳光体育运动”.短跑运动,可以锻炼人的灵活性,增强人的爆发力,因此小明和小亮在课外活动中,报名参加了短跑训练小组.在近几次百米训练中,所测成绩如图所示,请根据图中所示解答以下问题.
(1)请根据图中信息,补全下面的表格;
第1次 第2次 第3次 第4次 第5次
小明 13.3 13.4 13.3 ___ 13.3
小亮 13.2 ___ 13.1 13.5 13.3
(2)计算他们5次成绩的平均数和方差,若你是他们的教练,会分别给予他们怎样的建议
20、八(1)班组织了一次经典诵读比赛,甲、乙两队各10人的比赛成绩如下表:
甲 7 8 9 7 10 10 9 10 10 10
乙 10 8 7 9 8 10 10 9 10 9
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的方差;
(3)已知甲队成绩的方差是1.4,则成绩较为整齐的是 队.
21.如图是A、B两所学校艺术节期间收到的各类艺术作品的统计图:
(1) 从图中能否看出哪所学校收到的水粉画作品的数量多?为什么?
(2) 已知A学校收到的剪纸作品比B学校的多20件,收到的书法作品比B学校的少100件,请问这两所学校收到艺术作品的总数分别是多少件?
22.某校八年级为了解学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如下表,并绘制了如图所示的两幅不完整的统计图,已知B,E两组发言人数的比为5∶2,请结合图中相关数据回答下列问题:
(1)求出样本容量,并补全直方图;
(2)该年级共有学生500人,请估计全年级在这天中发言次数不少于12次的人数.
23. 某校举办了一次成语知识竞赛,满分10分,学生得分均为整数,成绩达到6分及6分以上为合格,达到9分或10分为优秀,这次竞赛中,甲、乙两组学生成绩分布的折线统计图和成绩统计分析表如下所示.
(1)求出下列成绩统计分析表中a,b的值:
组别 平均分 中位数 方差 合格率 优秀率
甲组 6.8 a 3.76 90% 30%
乙组 b 7.5 1.96 80% 20%
(2)小英同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上面表格判断,小英是甲、乙哪个组的学生;
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你写出两条支持乙组同学观点的理由.
24.为积极响应“弘扬传统文化”的号召,某学校倡导全校1 200名学生进行经典诗词诵背活动,并在活动之后举办经典诗词大赛,为了解本次系列活动的持续效果,学校团委在活动启动之初,随机抽取部分学生调查“一周诗词诵背数量”,根据调查结果绘制成的统计图(部分)如图所示.
大赛结束后一个月,再次抽查这部分学生“一周诗词诵背数量”,绘制成统计表
一周诗词诵背数量 3首 4首 5首 6首 7首 8首
人数 10 10 15 40 25 20
请根据调查的信息分析:
(1)活动启动之初学生“一周诗词诵背数量”的中位数为__ _;
(2)估计大赛后一个月该校学生一周诗词诵背6首(含6首)以上的人数;
(3)选择适当的统计量,从两个不同的角度分析两次调查的相关数据,评价该校经典诗词诵背系列活动的效果.
参考答案:
一.填空题
题号 1 2 3 4 5 6 7 8 9 10
答案 C A A B C A D D B D
二.选择题
11.解:∵数据1,5,n,6,8的众数是1,
∴n=1,
则这组数据为1、1、5、6、8,
∴这组数据的中位数为5,
故答案为:5.
12.解:该应聘者的综合成绩为88×40%+90×60%=89.2(分),
故答案为:89.2.
13.解:由题意知,第2组数据是在第1组数据的基础上每个数据都加上2的,
∴第2组数据的波动性与第1组数据的波动性相同,即S12=S22,
故答案为:等于.
14.9
15.11 点拨:(169-145)÷2.3≈10.43,采用进一法确定组数.
16.7.5;108°
17、某校规定:学生的数学期未总计成须由卷面成绩、研究性学习成绩、平时成绩三部分构成,各部分所占比例如图所示.小明本学期数学学科的卷面成绩、研究性学习成绩、平时成绩得分依次为分、分、分,则小明的数学期末总评成绩为________分.
【答案】87
【分析】
按统计图中各部分所占比例算出小明的期末数学总评成绩即可.
【详解】
解:小明的期末数学总评成绩=90×60%+80×20%+85×20%=87(分).
故答案为87.
18、“学习强国”是王老师每天的必修课,下表是王老师一周的学习得分情况:
日期 11.1 11.2 11.3 11.4 11.5 11.6 11.7
得分 49 60 48 42 55 55 55
则这组数据的众数为______.
【答案】55
【分析】众数是一组数据中出现次数最多的数.
【详解】55出现了3次,出现的次数最多,则众数是55;
故答案为:55.
三.解答题
19、少年学生走近操场,走到阳关下,积极参加体育锻炼,我国启动了“全国亿万学生阳光体育运动”.短跑运动,可以锻炼人的灵活性,增强人的爆发力,因此小明和小亮在课外活动中,报名参加了短跑训练小组.在近几次百米训练中,所测成绩如图所示,请根据图中所示解答以下问题.
(1)请根据图中信息,补全下面的表格;
第1次 第2次 第3次 第4次 第5次
小明 13.3 13.4 13.3 ___ 13.3
小亮 13.2 ___ 13.1 13.5 13.3
(2)计算他们5次成绩的平均数和方差,若你是他们的教练,会分别给予他们怎样的建议
【答案】(1)13.2,13.4;
(2)小明:平均数13.3,方差0.004;小亮:平均数13.3,方差0.02,两人的平均数相等,小亮的方差大,成绩不稳定,但获得过最好成绩比小明有潜力.
【分析】
(1)读折线统计图填上数据即可解答;
(2)根据平均数、方差进行计算,方差越大,波动越大,成绩越不稳定;反之也成立.
【详解】
解:(1)根据给出的图象可得:小明第4次的成绩是13.2;
小亮第2次的成绩是13.4;
故答案为:13.2,13.4;
(2)小明的平均成绩是:(13.3+13.4+13.3+13.2+13.3)÷5=13.3秒,
小亮的平均成绩是:(13.2+13.4+13.1+13.5+13.3)÷5=13.3秒;
小明的方差是:s2=[(13.3-13.3)2+(13.4-13.3)2+…+(13.3-13.3)2]÷5=0.004,
小亮的方差是:s2=[(13.2-13.3)2+(13.4-13.3)2+…+(13.3-13.3)2]÷5=0.02;
小明虽然成绩稳定,但是还需提高自己的最好成绩,小亮虽然跑出了他们两个的最好成绩,但是仍需加强成绩的稳定性.
20、八(1)班组织了一次经典诵读比赛,甲、乙两队各10人的比赛成绩如下表:
甲 7 8 9 7 10 10 9 10 10 10
乙 10 8 7 9 8 10 10 9 10 9
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的方差;
(3)已知甲队成绩的方差是1.4,则成绩较为整齐的是 队.
【答案】(1)9.5,10;(2);(3)乙
【分析】
(1)根据中位数的定义求出最中间两个数的平均数;根据众数的定义找出出现次数最多的数即可;
(2)先求出乙队的平均成绩,再根据方差公式进行计算;
(3)先比较出甲队和乙队的方差,再根据方差的意义即可得出答案.
【详解】
(1)把甲队的成绩从小到大排列为:7,7,8,9,9,10,10,10,10,10,最中间两个数的平均数是(9+10)÷2=9.5(分),
则中位数是9.5分;
乙队成绩中10出现了4次,出现的次数最多,
则乙队成绩的众数是10分;
故答案为:9.5,10;
(2)乙队的平均成绩是:×(10×4+8×2+7+9×3)=9,
则方差是:×[4×(10 9)2+2×(8 9)2+(7 9)2+3×(9 9)2]=1;
(3)∵甲队成绩的方差是1.4,乙队成绩的方差是1,
∴成绩较为整齐的是乙队;
故答案为:乙.
21.⑴.不能.因为在只知道各校水粉画作品的百分比而不知道总量的前提下,是不能进行比较的.
⑵设A、B两所学校收到艺术作品的总数分别是x件和y件则解之: 答略.
22. 解:(1)由题意得,E组为(10÷5)×2=4(人),发言人总数为4÷8%=50(人),A组为50×6%=3(人),C组为50×30%=15(人),D组为50×26%=13(人),∴F组为50-3-10-15-13-4=5(人),补全直方图略.
(2)∵在统计的50人中,发言次数不少于12次的有4+5=9(人),∴在这天发言次数不少于12次的频率为=18%,∴全年级500人中,在这天里发言次数不少于12次的人数为500×18%=90(人).
23. 解:(1)由折线统计图可知,甲组成绩从小到大排列为:3,6,6,6,6,6,7,9,9,10,
∴a=6,b==7.2.
(2)∵甲组的中位数为6,乙组的中位数为7.5,而小英的成绩位于小组中上游,∴小英属于甲组学生.
(3)①乙组的平均分高于甲组,即乙组的总体平均水平高;②乙组的方差比甲组小,即乙组的成绩比甲组的成绩稳定.
24. 解:(1)本次调查的学生有20÷=120(名),背诵4首的有120-15-20-16-13-11=45(人),∵15+45=60,∴这组数据的中位数是(4+5)÷2=4.5(首)
(2)大赛后一个月该校学生一周诗词诵背6首(含6首)以上的有1 200×=850(人),答:大赛后一个月该校学生一周诗词诵背6首(含6首)以上的有850人
(3)活动启动之初的中位数是4.5首,众数是4首,大赛比赛后一个月时的中位数是6首,众数是6首,由比赛前后的中位数和众数看,比赛后学生背诵诗词的积极性明显提高,这次举办后的效果比较理想
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
第二十章《数据的收集、整理与描述》单元检测题
题号 一 二 三 总分
19 20 21 22 23 24
分数
一、选择题(本大题共10小题,每小题3分,共计30分)
1. 九年级(1)班15名男同学进行引体向上测试,每人只测一次,测试结果统计如下:
引体向上数/个 0 1 2 3 4 5 6 7 8
人数 1 1 2 1 3 3 2 1 1
这15名男同学引体向上数的中位数是( )
A.2 B.3 C.4 D.5
2. 国产大飞机C919用数学建模的方法预测的价格是(单位:美元):5 098,5 099,5 001,5 002,4 990,4 920,5 080,5 010,4 901,4 902,这组数据的平均数是( )
A.5 000.3 B.4 999.7
C.4 997 D.5 003
3. 在光明中学组织的全校师生迎“五四”诗词大赛中,来自不同年级的25名参赛同学的得分情况如图所示.这些成绩的中位数和众数分别是( )
A.96分、98分 B. 97分、98分
C. 98分、96分 D. 97分、96分
4.一组数据:10,8,6,10,8,13,11,10,12,7,10,11,10,9,12,10,9,12,9,8,那么频率为0.3的范围是( )
A.6~7 B.8~9 C.10~11 D.12~13
5.为了了解本校七年级700名学生上学期参加社会实践活动的时间,
随机对该年级50名学生进行了调查.根据收集的数据绘制了频数分
布直方图,则以下说法正确的是( )
A.学生参加社会实践活动时间最多为16h
B. 学生参加社会实践活动时间大多数是12~14h
C. 学生参加社会实践活动时间不少于10h的为84%
D. 由样本可以估计全年级700人中参加社会实践活动时间为6~8h的大约有26人
(第5题)
6.下列选项中,显示部分在总体中所占百分比的统计图是( )
A.扇形图 B.条形图 C.折线图 D.直方图
7.某校开展“了解传统习俗,弘扬民族文化”为主题的实践活动.实践小组就“是否知道端午节的来由”这个问题,对部分学生进行了调查,调查结果如图所示,其中不知道的学生有8人.下列说法不正确的是( )
A.被调查的学生共50人
B.被调查的学生中“知道”的人数为32
C.图中“记不清”对应的圆心角为
D.全校“知道”的人数约占全校人数的64%
8.体育老师对九(1)班学生“你最喜欢的体育项目是什么?(只写一项)”的问题进行了调查,把所得数据绘制成条形统计图.由图可知,最喜欢篮球的百分比是( )
A.16% B.21%
C.30% D.40%
9.女子排球队6名场上队员的身高(单位:cm)是:170,174,178,180,180,184.现用身高178cm的队员替换场上身高174cm的队员,与换人前相比,场上队员的身高( )
A.平均数变大,中位数不变
B.平均数变大,中位数变大
C.平均数变小,中位数不变
D.平均数变小,中位数变大
10.在一次体育测试中,小明记录了本班10名同学一分钟跳绳的成绩,如表:
成绩 150 160 170 180 190
人数 2 3 2 2 1
对于这10名学生的跳绳成绩,下列说法错误的是( )
A.众数是160 B.中位数是165
C.平均数是167 D.方差是104.5
二、填空题(本大题共8小题,每小题3分,共24分)
11.样本数据1,5,n,6,8的众数是1,则这组数的中位数是 .
12.某地教育局拟招聘一批数学教师,现有一名应聘者笔试成绩88分、面试成绩90分,综合成绩按照笔试占40%、面试占60%进行计算,该应聘者的综合成绩为 分.
13.一组数1、2、3、4、5的方差是S12与另一组数3、4、5、6、7的方差S22的大小比较S12 S22(填写:大于、等于、小于).
14.某次测验后,60~70分这组人数占全班总人数的20%,若全班有45人,则该组的频数为________.
15.对某中学同龄的70名女生的身高进行测量后,得到一组数据,其中最大值为169 cm,最小值为145 cm,对这组数据进行整理后,确定它的组距为2.3 cm,则组数为________.
16.如图是某农场里三种蔬菜种植面积的扇形统计图,若西红柿种植面积为4.2公顷,则这三种蔬菜种植总面积是________公顷,表示黄瓜的扇形圆心角的度数为________.
17、某校规定:学生的数学期未总计成须由卷面成绩、研究性学习成绩、平时成绩三部分构成,各部分所占比例如图所示.小明本学期数学学科的卷面成绩、研究性学习成绩、平时成绩得分依次为分、分、分,则小明的数学期末总评成绩为________分.
18、“学习强国”是王老师每天的必修课,下表是王老师一周的学习得分情况:
日期 11.1 11.2 11.3 11.4 11.5 11.6 11.7
得分 49 60 48 42 55 55 55
则这组数据的众数为______.
三、解答题(本大题共46分,19题6分,20---24题每题8分)
19、少年学生走近操场,走到阳关下,积极参加体育锻炼,我国启动了“全国亿万学生阳光体育运动”.短跑运动,可以锻炼人的灵活性,增强人的爆发力,因此小明和小亮在课外活动中,报名参加了短跑训练小组.在近几次百米训练中,所测成绩如图所示,请根据图中所示解答以下问题.
(1)请根据图中信息,补全下面的表格;
第1次 第2次 第3次 第4次 第5次
小明 13.3 13.4 13.3 ___ 13.3
小亮 13.2 ___ 13.1 13.5 13.3
(2)计算他们5次成绩的平均数和方差,若你是他们的教练,会分别给予他们怎样的建议
20、八(1)班组织了一次经典诵读比赛,甲、乙两队各10人的比赛成绩如下表:
甲 7 8 9 7 10 10 9 10 10 10
乙 10 8 7 9 8 10 10 9 10 9
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的方差;
(3)已知甲队成绩的方差是1.4,则成绩较为整齐的是 队.
21.如图是A、B两所学校艺术节期间收到的各类艺术作品的统计图:
(1) 从图中能否看出哪所学校收到的水粉画作品的数量多?为什么?
(2) 已知A学校收到的剪纸作品比B学校的多20件,收到的书法作品比B学校的少100件,请问这两所学校收到艺术作品的总数分别是多少件?
22.某校八年级为了解学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如下表,并绘制了如图所示的两幅不完整的统计图,已知B,E两组发言人数的比为5∶2,请结合图中相关数据回答下列问题:
(1)求出样本容量,并补全直方图;
(2)该年级共有学生500人,请估计全年级在这天中发言次数不少于12次的人数.
23. 某校举办了一次成语知识竞赛,满分10分,学生得分均为整数,成绩达到6分及6分以上为合格,达到9分或10分为优秀,这次竞赛中,甲、乙两组学生成绩分布的折线统计图和成绩统计分析表如下所示.
(1)求出下列成绩统计分析表中a,b的值:
组别 平均分 中位数 方差 合格率 优秀率
甲组 6.8 a 3.76 90% 30%
乙组 b 7.5 1.96 80% 20%
(2)小英同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上面表格判断,小英是甲、乙哪个组的学生;
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你写出两条支持乙组同学观点的理由.
24.为积极响应“弘扬传统文化”的号召,某学校倡导全校1 200名学生进行经典诗词诵背活动,并在活动之后举办经典诗词大赛,为了解本次系列活动的持续效果,学校团委在活动启动之初,随机抽取部分学生调查“一周诗词诵背数量”,根据调查结果绘制成的统计图(部分)如图所示.
大赛结束后一个月,再次抽查这部分学生“一周诗词诵背数量”,绘制成统计表
一周诗词诵背数量 3首 4首 5首 6首 7首 8首
人数 10 10 15 40 25 20
请根据调查的信息分析:
(1)活动启动之初学生“一周诗词诵背数量”的中位数为__ _;
(2)估计大赛后一个月该校学生一周诗词诵背6首(含6首)以上的人数;
(3)选择适当的统计量,从两个不同的角度分析两次调查的相关数据,评价该校经典诗词诵背系列活动的效果.
参考答案:
一.填空题
题号 1 2 3 4 5 6 7 8 9 10
答案 C A A B C A D D B D
二.选择题
11.解:∵数据1,5,n,6,8的众数是1,
∴n=1,
则这组数据为1、1、5、6、8,
∴这组数据的中位数为5,
故答案为:5.
12.解:该应聘者的综合成绩为88×40%+90×60%=89.2(分),
故答案为:89.2.
13.解:由题意知,第2组数据是在第1组数据的基础上每个数据都加上2的,
∴第2组数据的波动性与第1组数据的波动性相同,即S12=S22,
故答案为:等于.
14.9
15.11 点拨:(169-145)÷2.3≈10.43,采用进一法确定组数.
16.7.5;108°
17、某校规定:学生的数学期未总计成须由卷面成绩、研究性学习成绩、平时成绩三部分构成,各部分所占比例如图所示.小明本学期数学学科的卷面成绩、研究性学习成绩、平时成绩得分依次为分、分、分,则小明的数学期末总评成绩为________分.
【答案】87
【分析】
按统计图中各部分所占比例算出小明的期末数学总评成绩即可.
【详解】
解:小明的期末数学总评成绩=90×60%+80×20%+85×20%=87(分).
故答案为87.
18、“学习强国”是王老师每天的必修课,下表是王老师一周的学习得分情况:
日期 11.1 11.2 11.3 11.4 11.5 11.6 11.7
得分 49 60 48 42 55 55 55
则这组数据的众数为______.
【答案】55
【分析】众数是一组数据中出现次数最多的数.
【详解】55出现了3次,出现的次数最多,则众数是55;
故答案为:55.
三.解答题
19、少年学生走近操场,走到阳关下,积极参加体育锻炼,我国启动了“全国亿万学生阳光体育运动”.短跑运动,可以锻炼人的灵活性,增强人的爆发力,因此小明和小亮在课外活动中,报名参加了短跑训练小组.在近几次百米训练中,所测成绩如图所示,请根据图中所示解答以下问题.
(1)请根据图中信息,补全下面的表格;
第1次 第2次 第3次 第4次 第5次
小明 13.3 13.4 13.3 ___ 13.3
小亮 13.2 ___ 13.1 13.5 13.3
(2)计算他们5次成绩的平均数和方差,若你是他们的教练,会分别给予他们怎样的建议
【答案】(1)13.2,13.4;
(2)小明:平均数13.3,方差0.004;小亮:平均数13.3,方差0.02,两人的平均数相等,小亮的方差大,成绩不稳定,但获得过最好成绩比小明有潜力.
【分析】
(1)读折线统计图填上数据即可解答;
(2)根据平均数、方差进行计算,方差越大,波动越大,成绩越不稳定;反之也成立.
【详解】
解:(1)根据给出的图象可得:小明第4次的成绩是13.2;
小亮第2次的成绩是13.4;
故答案为:13.2,13.4;
(2)小明的平均成绩是:(13.3+13.4+13.3+13.2+13.3)÷5=13.3秒,
小亮的平均成绩是:(13.2+13.4+13.1+13.5+13.3)÷5=13.3秒;
小明的方差是:s2=[(13.3-13.3)2+(13.4-13.3)2+…+(13.3-13.3)2]÷5=0.004,
小亮的方差是:s2=[(13.2-13.3)2+(13.4-13.3)2+…+(13.3-13.3)2]÷5=0.02;
小明虽然成绩稳定,但是还需提高自己的最好成绩,小亮虽然跑出了他们两个的最好成绩,但是仍需加强成绩的稳定性.
20、八(1)班组织了一次经典诵读比赛,甲、乙两队各10人的比赛成绩如下表:
甲 7 8 9 7 10 10 9 10 10 10
乙 10 8 7 9 8 10 10 9 10 9
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的方差;
(3)已知甲队成绩的方差是1.4,则成绩较为整齐的是 队.
【答案】(1)9.5,10;(2);(3)乙
【分析】
(1)根据中位数的定义求出最中间两个数的平均数;根据众数的定义找出出现次数最多的数即可;
(2)先求出乙队的平均成绩,再根据方差公式进行计算;
(3)先比较出甲队和乙队的方差,再根据方差的意义即可得出答案.
【详解】
(1)把甲队的成绩从小到大排列为:7,7,8,9,9,10,10,10,10,10,最中间两个数的平均数是(9+10)÷2=9.5(分),
则中位数是9.5分;
乙队成绩中10出现了4次,出现的次数最多,
则乙队成绩的众数是10分;
故答案为:9.5,10;
(2)乙队的平均成绩是:×(10×4+8×2+7+9×3)=9,
则方差是:×[4×(10 9)2+2×(8 9)2+(7 9)2+3×(9 9)2]=1;
(3)∵甲队成绩的方差是1.4,乙队成绩的方差是1,
∴成绩较为整齐的是乙队;
故答案为:乙.
21.⑴.不能.因为在只知道各校水粉画作品的百分比而不知道总量的前提下,是不能进行比较的.
⑵设A、B两所学校收到艺术作品的总数分别是x件和y件则解之: 答略.
22. 解:(1)由题意得,E组为(10÷5)×2=4(人),发言人总数为4÷8%=50(人),A组为50×6%=3(人),C组为50×30%=15(人),D组为50×26%=13(人),∴F组为50-3-10-15-13-4=5(人),补全直方图略.
(2)∵在统计的50人中,发言次数不少于12次的有4+5=9(人),∴在这天发言次数不少于12次的频率为=18%,∴全年级500人中,在这天里发言次数不少于12次的人数为500×18%=90(人).
23. 解:(1)由折线统计图可知,甲组成绩从小到大排列为:3,6,6,6,6,6,7,9,9,10,
∴a=6,b==7.2.
(2)∵甲组的中位数为6,乙组的中位数为7.5,而小英的成绩位于小组中上游,∴小英属于甲组学生.
(3)①乙组的平均分高于甲组,即乙组的总体平均水平高;②乙组的方差比甲组小,即乙组的成绩比甲组的成绩稳定.
24. 解:(1)本次调查的学生有20÷=120(名),背诵4首的有120-15-20-16-13-11=45(人),∵15+45=60,∴这组数据的中位数是(4+5)÷2=4.5(首)
(2)大赛后一个月该校学生一周诗词诵背6首(含6首)以上的有1 200×=850(人),答:大赛后一个月该校学生一周诗词诵背6首(含6首)以上的有850人
(3)活动启动之初的中位数是4.5首,众数是4首,大赛比赛后一个月时的中位数是6首,众数是6首,由比赛前后的中位数和众数看,比赛后学生背诵诗词的积极性明显提高,这次举办后的效果比较理想
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
