揭阳市2005-2006学年度高中二年级学年会考数学试题(理科)[下学期]
文档属性
| 名称 | 揭阳市2005-2006学年度高中二年级学年会考数学试题(理科)[下学期] |

|
|
| 格式 | zip | ||
| 文件大小 | 192.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-02-01 00:00:00 | ||
图片预览



文档简介
揭阳市2005-2006学年度高中二年级学年会考
数学试题(理科)
(测试时间120分钟,满分150分)
第Ⅰ卷(选择题共60分)
注意事项:
1.答卷前,考生务必将自己的姓名、考生号,用钢笔或签字笔填写在答题卡密封线内。
2.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡指定区域内的相应位
置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.在复平面内,复数的共轭复数对应的点位于( )
A.第一象限 B.第二象限 C. 第三象限 D. 第四象限
2.在右图的电路图中,闭合开关A是灯泡B亮的( )
A.充要条件 B.充分不必要条件
C.必要不充分条件 D.既不充分也不必要条件
3.若函数是奇函数,当x>0时,其对应的图象如图,
则为( )
A. B. C. D.
4.一个球的外接正方体的体积是8,则这个球的表面积是( )
A B C D
5.如图,设A、B两点在河的两岸,一测量者在A的同
侧,在所在的河岸边选定一点C,测出AC的距离为50m,
∠ ACB=45°,∠CAB=105°后,就可以计算出A、B
两点的距离为( )
A. B. C. D.
6.中心在原点,过点,离心率为的双曲线方程是( )
A. B. C. D.
7.已知,则在上的射影为( )
A. B. C. D.
8.命题:①使, ②对
③对, ④使
其中真命题为( )
A. ③ B. ③④ C. ②③④ D.①②③④
9. 某工厂工人月工资y(单位:元)随劳动生产率x(单位:千元)变化的回归直线方程为=90x+60,则下列说法正确的是( )
A. 劳动生产率为1000元时,工人月工资为150元;
B. 劳动生产率提高1000元时,工人月工资约提高90元 ;
C. 劳动生产率提高1000元时,工人月工资约提高150元 ;
D. 当工人月工资为300元时,劳动生产率为27060元.
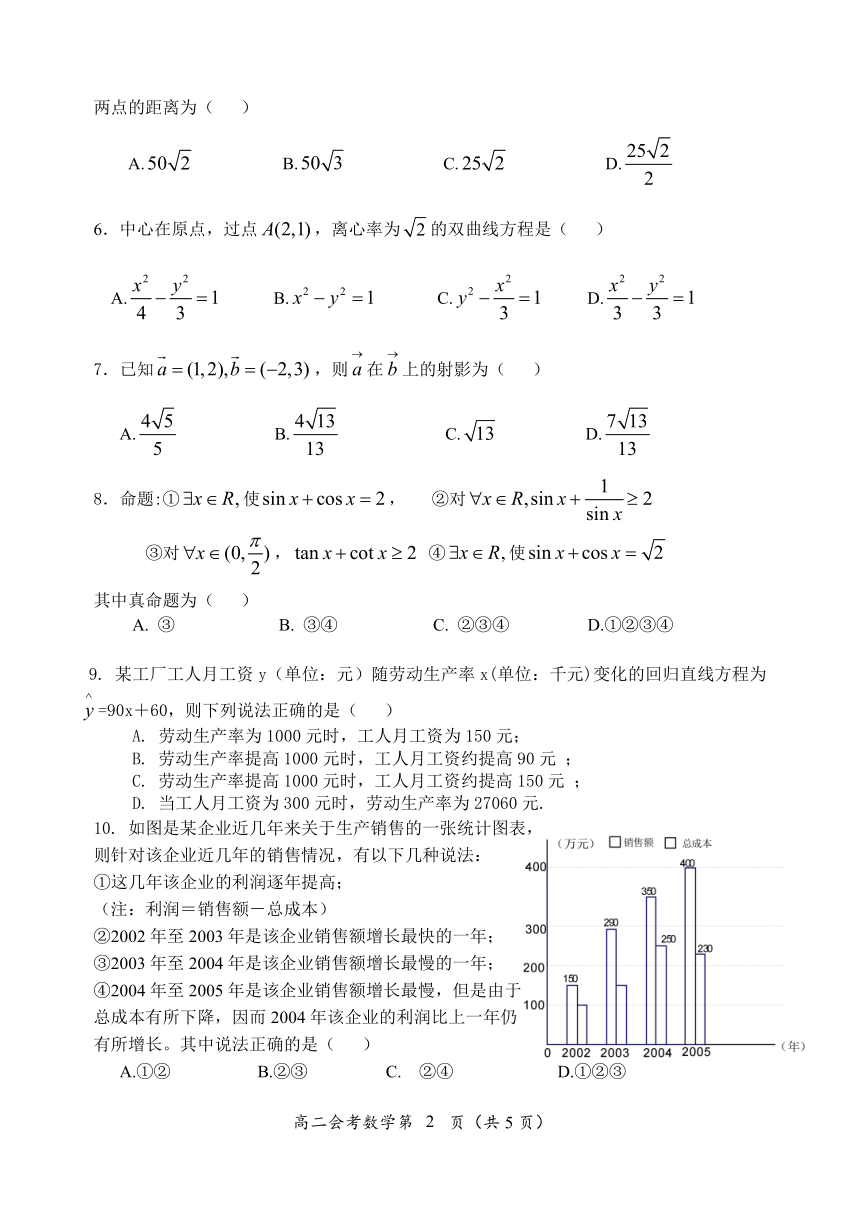
10. 如图是某企业近几年来关于生产销售的一张统计图表,
则针对该企业近几年的销售情况,有以下几种说法:
①这几年该企业的利润逐年提高;
(注:利润=销售额-总成本)
②2002年至2003年是该企业销售额增长最快的一年;
③2003年至2004年是该企业销售额增长最慢的一年;
④2004年至2005年是该企业销售额增长最慢,但是由于
总成本有所下降,因而2004年该企业的利润比上一年仍
有所增长。其中说法正确的是( )
A.①② B.②③ C. ②④ D.①②③
11.定积分的值为( )
A. B. C. D.
a1 a2 a3
a4 a5 a6
a7 a8 a9
12.右表是在3×3的空格中填入a1到a9九个正数,且使得每一行都成等差数列,每一列都成等比数列,若a1=1,a3=3,a9=12,则
a7应是( )
A.2 B.4 C.5 D.6
第Ⅱ卷(非选择题共90分)
二、填空题:本大题共4小题,每小题4分,共16分,把答案填在答题卡的相应横线上.
13. 定义运算,则= .
14.右图中的算法输出的结果是 .
15.一辆列车沿直线轨道前进,从刹车开始到停车这段时间内,
测得刹车后秒内列车前进的距离为米,则列
车刹车后 秒停下来,期间列车前进了 米.
16. 如图,平面内有三点,A(0,1),B(-2,0),C(2,0),请你构造函数
或曲线的方程,使其图象经过这三点。你构造的函数关系式或曲
线的方程分别为
.
(说明:函数的关系式或曲线的方程至少
写出2个,2个都正确给4分,少写不给分,
多写部分正确的每个加1分,但全卷总分不
超过150分)
第16题图 第14题图
三、解答题:本大题共6小题,共74分。解答应写出文字说明,证明过程或演算步骤。
17.(本题满分10分)
已知:向量,。
求函数f(x)的最小正周期和值域.
18.(本小题满分12分)
已知函数.
(Ⅰ) 求函数f(x)的单调区间;
(Ⅱ)求函数f(x)的极值。
19. (本题满分12分)
一医院从4名男医生和2名女医生中选出3人加入医疗队,赴某地震灾区参加救援工作。设随机变量表示所选3人中女医生的人数。
(I) 求的分布列;
(II) 求的数学期望和方差。
20.(本题满分12分)
如图,正方形中,分别是的中点,现沿及把这个正方形折成一个四面体,使三点重合,重合后的点记为,则在四面体中
(Ⅰ)求证:;
(Ⅱ)请指出四面体中有哪些平面互相垂直;
(Ⅲ)若分别是的中点,求异面直线与所成的角的余弦值。
21.(本题满分14分)
在梯形ABCD中,AB⊥AD,AB∥CD,A、B是两个定点,其坐
标分别为(0,-1)、(0,1),C、D是两个动点,且满足|CD|=|BC|.
(Ⅰ)求动点C的轨迹E的方程;
(Ⅱ)试探究在轨迹E上是否在一点P?使得P到直线y=x-2的
距离最短;
(Ⅲ)设轨迹E与直线所围成的图形的
面积为S,试求S的最大值。
22. (本题满分14分)
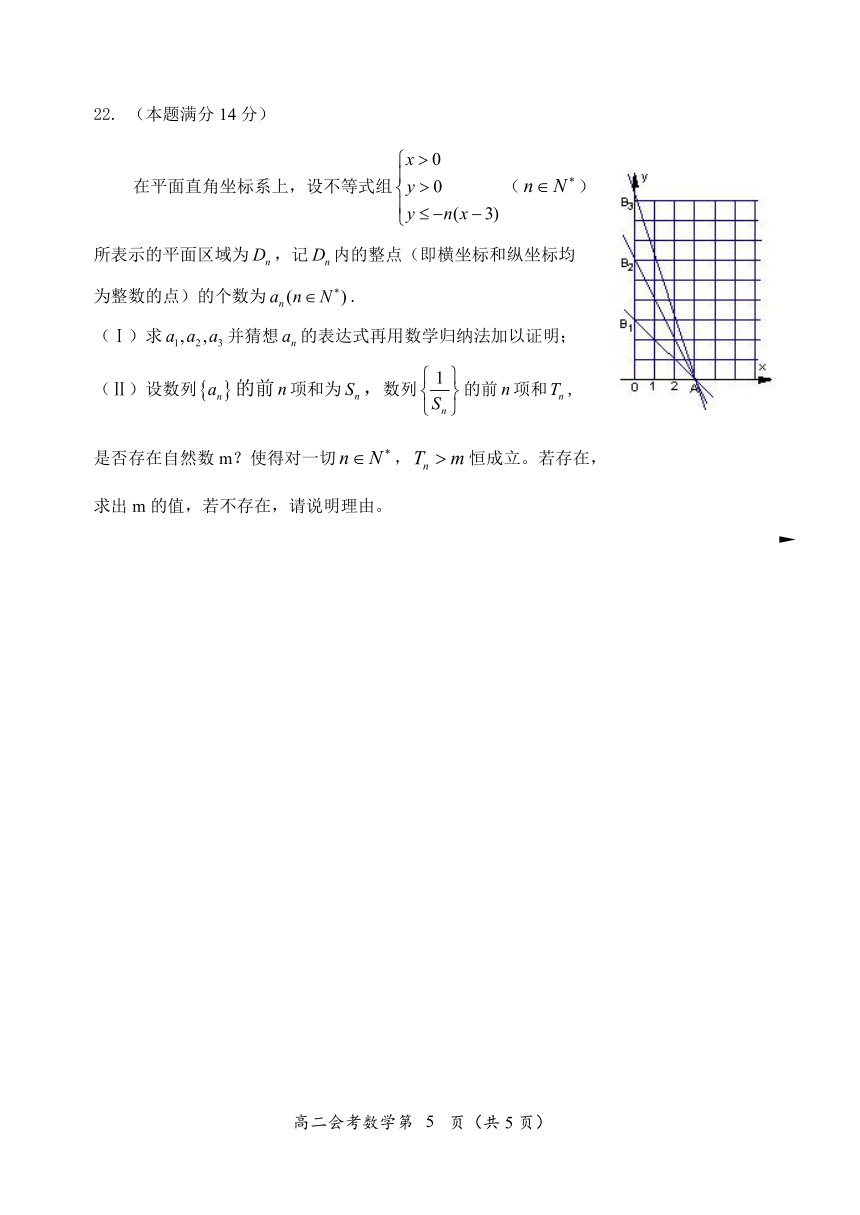
在平面直角坐标系上,设不等式组()
所表示的平面区域为,记内的整点(即横坐标和纵坐标均
为整数的点)的个数为.
(Ⅰ)求并猜想的表达式再用数学归纳法加以证明;
(Ⅱ)设数列的前项和为,数列的前项和,
是否存在自然数m?使得对一切,恒成立。若存在,
求出m的值,若不存在,请说明理由。
参考答案及评分说明
一.选择题:CBBCA DDBBC AB
解析:3.由图象可得g(x)=2x-3,因函数的图象关于原点对称,可得f(x)=2x+3,选B.
4.∵球的外切正方体的体积是8,∴正方体的棱长为2,它的内切球的半径为1,其表面积为。
5.由正弦定理得
6.由离心率为,设方程,代入得∴选D
8.在上的射影为:.选B.
9. 由=90(x+1)+60=(90x+60)+90知答案选B.
11.,选A.
12.用筛选法。或由题意可得:a2=2,a62=a3a9,a6=6,a42=a7,2a5=a4+a6,
2a8=a7+a9,a52=a2a8,解得,故选B.
二.填空题:
13. ;14.5050 ;15.30、405 ;16.参考答案: ,,,,等等.
解析:13.由定义得:
14.输出的结果为:1+2+3+……+100=5050
15.解法1:,由瞬时速度得(秒),期间列车前进了(米).
解法2: 刹车后列车前进的距离达到最大时,列车停止,这时(秒)
列车前进的距离.
三.解答题:
17.解:
-------------------------2分
--------------------4分
---------------6分
-----------------------------8分
∴函数f(x)的最小正周期为,值域为[-2,2] --------------10分
18.解: (Ⅰ) 由得
= -----------------2分
当得
∴或,即函数f(x)的单调增区间为------4分
当得,∴函数f(x)的单调减区间为(-1,3)-----6分
(Ⅱ)令得或,---------------8分
由(Ⅰ)知,函数f(x)在单调递增,在(-1,3)上单调递减,
∴当时,f(x)有极大值,f(x)极大=f(-1)= ----------10分
∵函数f(x)在(-1,3)上单调递减,在上递增,
∴当x=3时,f(x)有极小值,f(x)极小=f(3)=-9 ------------12分
19.(I)解:∵可能取的值为。
--------------------------- ----3分
∴的分布列为
0 1 2
P
-----------------6分
(II)解:由(I),的数学期望为
---------------------------9分
--------------------12分
20.(Ⅰ)证明:在折前正方形中,, ……1分
折成四面体后,, ……3分
又 ……4分
(Ⅱ) ……7分
(Ⅲ)解法1:取EF的中点A,连AM,AN,
由M是SF的中点 MA∥SE
为异面直线与所成的角;……9分
设正方形边长为,
又,AN=, ……10分
取GF中点B在△MBN中MN= ……11分
在△MNA中 ……12分
解法2:∵,EG⊥GF
以点G为原点建立空间直角坐标系如图示,
设正方形边长为,则G(0,0,0),E(a,0,0),
F(0,a,0)S(0,0,2a),M(0,,a),
N(,0,0)
∴,
∴
21.(Ⅰ) 解法1:依题意知,CD⊥AD,且|CD|=|BC|.依抛物线的定义可知点C的轨迹是
以B为焦点,以AD为准线的抛物线除去顶点和与直线y=1的交点。 -----------2分
∵|OB|=1 ∴C的轨迹E的方程为x2=4y(x≠0,x≠) -------------4分
解法2:设C(x,y)则|CD|=y+1,|CB|=,
又|CD|=|BC|. ,化简得:
x2=4y(x≠0,x≠)
(Ⅱ)解法1:设P(x,y)是轨迹E上一点,则P到直线y=x-2的距离
当x=2时,d取得最小值,这时x=2,y=1, ---------------------7分
即点P(2,1).但由(Ⅰ)知点(2,1)不在轨迹E上,
∴在轨迹E上这样的点P不存在。 -------------------------------8分
解法2:所求点即与直线y=x-2平行的轨迹E的切线与E的切点,
由得, ,∴,
下同解法1。
解法3:设与直线y=x-2 平行,与抛物线E相切的直线为
x-y+m=0,由方程组
有一解得方程 有两个相等的实根
∴ ∴m=-1从而得方程组的解为,下同上.
(Ⅲ) ∵-2根据图形结合定积分的几何意义可得:
----------------------------11分
----------------------------13分
当时,。 ------------- --------------14分
其它解法请参照给分。
22.解:(Ⅰ)当n=1时,D1为Rt△OAB1的内部包括斜边,这时,
当n=2时,D2为Rt△OAB2的内部包括斜边,这时,
当n=3时,D3为Rt△OAB3的内部包括斜边,这时,……, ---3分
由此可猜想=3n。 --------------------------------------------------4分
下面用数学归纳法证明:
当n=1时,猜想显然成立。
假设当n=k时,猜想成立,即,() ----5分
平面区域为Rt、平面区域为Rt△
如图,∵平面区域比平面区域多3个整点, ------- 7分
即当n=k+1时,,这就是说当n=k+1时,
猜想也成立,
由(1)、(2)知=3n对一切都成立。 ---------------------8分
(Ⅱ)∵=3n, ∴数列是首项为3,公差为3的等差数列,
∴.
-------------------------10分
== -------------------------------11分
∵对一切,恒成立, ∴
∵在上为增函数 ∴ ---13分
,满足的自然数为0,
∴满足题设的自然数m存在,其值为0。 -------------------------14分
PAGE
7
高二会考数学第 页(共5页)
数学试题(理科)
(测试时间120分钟,满分150分)
第Ⅰ卷(选择题共60分)
注意事项:
1.答卷前,考生务必将自己的姓名、考生号,用钢笔或签字笔填写在答题卡密封线内。
2.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡指定区域内的相应位
置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.在复平面内,复数的共轭复数对应的点位于( )
A.第一象限 B.第二象限 C. 第三象限 D. 第四象限
2.在右图的电路图中,闭合开关A是灯泡B亮的( )
A.充要条件 B.充分不必要条件
C.必要不充分条件 D.既不充分也不必要条件
3.若函数是奇函数,当x>0时,其对应的图象如图,
则为( )
A. B. C. D.
4.一个球的外接正方体的体积是8,则这个球的表面积是( )
A B C D
5.如图,设A、B两点在河的两岸,一测量者在A的同
侧,在所在的河岸边选定一点C,测出AC的距离为50m,
∠ ACB=45°,∠CAB=105°后,就可以计算出A、B
两点的距离为( )
A. B. C. D.
6.中心在原点,过点,离心率为的双曲线方程是( )
A. B. C. D.
7.已知,则在上的射影为( )
A. B. C. D.
8.命题:①使, ②对
③对, ④使
其中真命题为( )
A. ③ B. ③④ C. ②③④ D.①②③④
9. 某工厂工人月工资y(单位:元)随劳动生产率x(单位:千元)变化的回归直线方程为=90x+60,则下列说法正确的是( )
A. 劳动生产率为1000元时,工人月工资为150元;
B. 劳动生产率提高1000元时,工人月工资约提高90元 ;
C. 劳动生产率提高1000元时,工人月工资约提高150元 ;
D. 当工人月工资为300元时,劳动生产率为27060元.
10. 如图是某企业近几年来关于生产销售的一张统计图表,
则针对该企业近几年的销售情况,有以下几种说法:
①这几年该企业的利润逐年提高;
(注:利润=销售额-总成本)
②2002年至2003年是该企业销售额增长最快的一年;
③2003年至2004年是该企业销售额增长最慢的一年;
④2004年至2005年是该企业销售额增长最慢,但是由于
总成本有所下降,因而2004年该企业的利润比上一年仍
有所增长。其中说法正确的是( )
A.①② B.②③ C. ②④ D.①②③
11.定积分的值为( )
A. B. C. D.
a1 a2 a3
a4 a5 a6
a7 a8 a9
12.右表是在3×3的空格中填入a1到a9九个正数,且使得每一行都成等差数列,每一列都成等比数列,若a1=1,a3=3,a9=12,则
a7应是( )
A.2 B.4 C.5 D.6
第Ⅱ卷(非选择题共90分)
二、填空题:本大题共4小题,每小题4分,共16分,把答案填在答题卡的相应横线上.
13. 定义运算,则= .
14.右图中的算法输出的结果是 .
15.一辆列车沿直线轨道前进,从刹车开始到停车这段时间内,
测得刹车后秒内列车前进的距离为米,则列
车刹车后 秒停下来,期间列车前进了 米.
16. 如图,平面内有三点,A(0,1),B(-2,0),C(2,0),请你构造函数
或曲线的方程,使其图象经过这三点。你构造的函数关系式或曲
线的方程分别为
.
(说明:函数的关系式或曲线的方程至少
写出2个,2个都正确给4分,少写不给分,
多写部分正确的每个加1分,但全卷总分不
超过150分)
第16题图 第14题图
三、解答题:本大题共6小题,共74分。解答应写出文字说明,证明过程或演算步骤。
17.(本题满分10分)
已知:向量,。
求函数f(x)的最小正周期和值域.
18.(本小题满分12分)
已知函数.
(Ⅰ) 求函数f(x)的单调区间;
(Ⅱ)求函数f(x)的极值。
19. (本题满分12分)
一医院从4名男医生和2名女医生中选出3人加入医疗队,赴某地震灾区参加救援工作。设随机变量表示所选3人中女医生的人数。
(I) 求的分布列;
(II) 求的数学期望和方差。
20.(本题满分12分)
如图,正方形中,分别是的中点,现沿及把这个正方形折成一个四面体,使三点重合,重合后的点记为,则在四面体中
(Ⅰ)求证:;
(Ⅱ)请指出四面体中有哪些平面互相垂直;
(Ⅲ)若分别是的中点,求异面直线与所成的角的余弦值。
21.(本题满分14分)
在梯形ABCD中,AB⊥AD,AB∥CD,A、B是两个定点,其坐
标分别为(0,-1)、(0,1),C、D是两个动点,且满足|CD|=|BC|.
(Ⅰ)求动点C的轨迹E的方程;
(Ⅱ)试探究在轨迹E上是否在一点P?使得P到直线y=x-2的
距离最短;
(Ⅲ)设轨迹E与直线所围成的图形的
面积为S,试求S的最大值。
22. (本题满分14分)
在平面直角坐标系上,设不等式组()
所表示的平面区域为,记内的整点(即横坐标和纵坐标均
为整数的点)的个数为.
(Ⅰ)求并猜想的表达式再用数学归纳法加以证明;
(Ⅱ)设数列的前项和为,数列的前项和,
是否存在自然数m?使得对一切,恒成立。若存在,
求出m的值,若不存在,请说明理由。
参考答案及评分说明
一.选择题:CBBCA DDBBC AB
解析:3.由图象可得g(x)=2x-3,因函数的图象关于原点对称,可得f(x)=2x+3,选B.
4.∵球的外切正方体的体积是8,∴正方体的棱长为2,它的内切球的半径为1,其表面积为。
5.由正弦定理得
6.由离心率为,设方程,代入得∴选D
8.在上的射影为:.选B.
9. 由=90(x+1)+60=(90x+60)+90知答案选B.
11.,选A.
12.用筛选法。或由题意可得:a2=2,a62=a3a9,a6=6,a42=a7,2a5=a4+a6,
2a8=a7+a9,a52=a2a8,解得,故选B.
二.填空题:
13. ;14.5050 ;15.30、405 ;16.参考答案: ,,,,等等.
解析:13.由定义得:
14.输出的结果为:1+2+3+……+100=5050
15.解法1:,由瞬时速度得(秒),期间列车前进了(米).
解法2: 刹车后列车前进的距离达到最大时,列车停止,这时(秒)
列车前进的距离.
三.解答题:
17.解:
-------------------------2分
--------------------4分
---------------6分
-----------------------------8分
∴函数f(x)的最小正周期为,值域为[-2,2] --------------10分
18.解: (Ⅰ) 由得
= -----------------2分
当得
∴或,即函数f(x)的单调增区间为------4分
当得,∴函数f(x)的单调减区间为(-1,3)-----6分
(Ⅱ)令得或,---------------8分
由(Ⅰ)知,函数f(x)在单调递增,在(-1,3)上单调递减,
∴当时,f(x)有极大值,f(x)极大=f(-1)= ----------10分
∵函数f(x)在(-1,3)上单调递减,在上递增,
∴当x=3时,f(x)有极小值,f(x)极小=f(3)=-9 ------------12分
19.(I)解:∵可能取的值为。
--------------------------- ----3分
∴的分布列为
0 1 2
P
-----------------6分
(II)解:由(I),的数学期望为
---------------------------9分
--------------------12分
20.(Ⅰ)证明:在折前正方形中,, ……1分
折成四面体后,, ……3分
又 ……4分
(Ⅱ) ……7分
(Ⅲ)解法1:取EF的中点A,连AM,AN,
由M是SF的中点 MA∥SE
为异面直线与所成的角;……9分
设正方形边长为,
又,AN=, ……10分
取GF中点B在△MBN中MN= ……11分
在△MNA中 ……12分
解法2:∵,EG⊥GF
以点G为原点建立空间直角坐标系如图示,
设正方形边长为,则G(0,0,0),E(a,0,0),
F(0,a,0)S(0,0,2a),M(0,,a),
N(,0,0)
∴,
∴
21.(Ⅰ) 解法1:依题意知,CD⊥AD,且|CD|=|BC|.依抛物线的定义可知点C的轨迹是
以B为焦点,以AD为准线的抛物线除去顶点和与直线y=1的交点。 -----------2分
∵|OB|=1 ∴C的轨迹E的方程为x2=4y(x≠0,x≠) -------------4分
解法2:设C(x,y)则|CD|=y+1,|CB|=,
又|CD|=|BC|. ,化简得:
x2=4y(x≠0,x≠)
(Ⅱ)解法1:设P(x,y)是轨迹E上一点,则P到直线y=x-2的距离
当x=2时,d取得最小值,这时x=2,y=1, ---------------------7分
即点P(2,1).但由(Ⅰ)知点(2,1)不在轨迹E上,
∴在轨迹E上这样的点P不存在。 -------------------------------8分
解法2:所求点即与直线y=x-2平行的轨迹E的切线与E的切点,
由得, ,∴,
下同解法1。
解法3:设与直线y=x-2 平行,与抛物线E相切的直线为
x-y+m=0,由方程组
有一解得方程 有两个相等的实根
∴ ∴m=-1从而得方程组的解为,下同上.
(Ⅲ) ∵-2
----------------------------11分
----------------------------13分
当时,。 ------------- --------------14分
其它解法请参照给分。
22.解:(Ⅰ)当n=1时,D1为Rt△OAB1的内部包括斜边,这时,
当n=2时,D2为Rt△OAB2的内部包括斜边,这时,
当n=3时,D3为Rt△OAB3的内部包括斜边,这时,……, ---3分
由此可猜想=3n。 --------------------------------------------------4分
下面用数学归纳法证明:
当n=1时,猜想显然成立。
假设当n=k时,猜想成立,即,() ----5分
平面区域为Rt、平面区域为Rt△
如图,∵平面区域比平面区域多3个整点, ------- 7分
即当n=k+1时,,这就是说当n=k+1时,
猜想也成立,
由(1)、(2)知=3n对一切都成立。 ---------------------8分
(Ⅱ)∵=3n, ∴数列是首项为3,公差为3的等差数列,
∴.
-------------------------10分
== -------------------------------11分
∵对一切,恒成立, ∴
∵在上为增函数 ∴ ---13分
,满足的自然数为0,
∴满足题设的自然数m存在,其值为0。 -------------------------14分
PAGE
7
高二会考数学第 页(共5页)
同课章节目录
