第三章 §3.4 函数的应用(一)高中数学人教A版必修一 课件(共23张PPT)
文档属性
| 名称 | 第三章 §3.4 函数的应用(一)高中数学人教A版必修一 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-26 20:16:28 | ||
图片预览








文档简介
(共23张PPT)
§3.4 函数的应用(一)
第三章 函数的概念与性质
学习目标
1.初步体会一次函数、二次函数、幂函数、分段函数模型的广泛应用,能运用函数思想处理现实生活中的简单应用问题.(重点)
2.能将实际问题转化为熟悉的模型,建立合适的数学模型解决简单的实际问题.(难点)
导语
2022年是中国共产主义青年团成立100周年.习主席曾寄语青年:“对想做、爱做的事要敢试敢为,努力从无到有、从小到大,把理想变为现实.要敢于做先锋,而不做过客、当看客,让创新成为青春远航的动力,让创业成为青春搏击的能量,让青春年华在为国家、为人民的奉献中焕发出绚丽光彩.”某学校成立了“团员先锋队”去参加建模比赛,你能在我们的日常生活中找到我们所学的函数模型吗?
一、一次函数模型的应用
二、二次函数模型的应用
三、分段函数模型的应用
随堂演练
内容索引
一次函数模型的应用
一
例1
为了发展电信事业,方便用户,电信公司对移动电话采用不同的收费方式,其中所使用的“如意卡”与“便民卡”在某市范围内每月(30天)的通话时间x(分)与通话费用y(元)
的关系如图所示.
(1)分别求出通话费用y1,y2与通话
时间x之间的函数解析式;
由图象可设y1=k1x+30(k1≠0),y2=k2x(k2≠0),
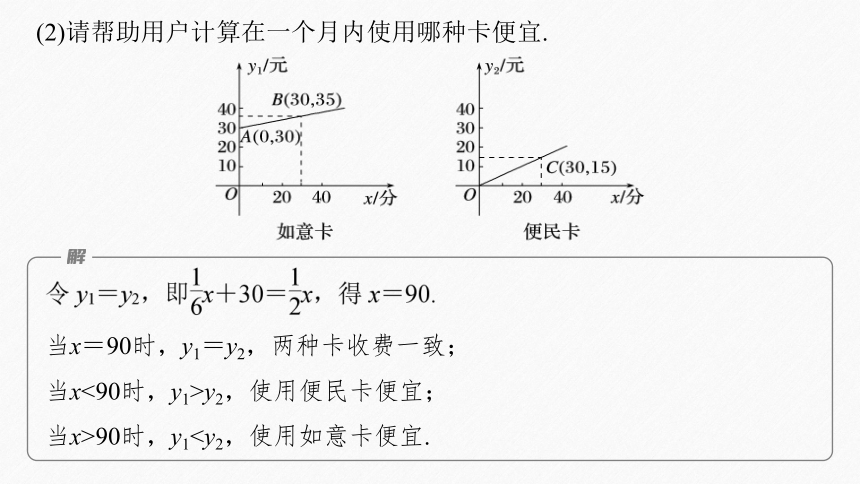
(2)请帮助用户计算在一个月内使用哪种卡便宜.
当x=90时,y1=y2,两种卡收费一致;
当x<90时,y1>y2,使用便民卡便宜;
当x>90时,y1反思感悟
一次函数模型的特点和求解方法
(1)一次函数模型的突出特点是其图象是一条直线(或一部分).
(2)解一次函数模型时,一般是借助两个点来确定,常用待定系数法.主要步骤是:设元、列式、求解.
跟踪训练1
某公司市场营销人员的个人月收入与其每月的销售量成一次函数关系,其图象如图所示,由图中给出的信息可知,营销人员没有销售量的收入是
A.3 100元 B.3 000元
C.2 900元 D.2 800元
√
设y=kx+b(k≠0),代入(1,8 000)和(2,13 000),
所以y=5 000x+3 000,当x=0时,y=3 000.
二次函数模型的应用
二
例2
设可获得总利润为R(x)万元,
∵R(x)在[0,210]上单调递增,
∴当年产量为210吨时,可获得最大利润1 660万元.
反思感悟
二次函数模型的应用策略
(1)常见问题:有些问题的两变量之间是二次函数关系,如面积问题、利润问题、产量问题、用料问题等,应构建二次函数模型求解.
(2)常用方法:根据实际问题建立二次函数模型解析式后,可利用配方法、判别式法、换元法以及二次函数的图象与单调性等方法求最值,也可以根据函数图象的对称轴与函数定义域的对应区间之间的位置关系讨论求解.
(3)特别注意:取得最值时的自变量的取值与实际意义是否相符.
跟踪训练2
某桶装水经营部每天的房租、人员工资等固定成本为200元,每桶水的进价是5元,销售单价与日均销售量的关系如表所示:
销售单价/元 6 7 8 9 10 11 12
日均销售量/桶 480 440 400 360 320 280 240
请根据以上数据作出分析,这个经营部怎样定价才能获得最大利润?
由表中数据可知,销售单价每增加1元,日均销售量就减少40桶,
设在进价的基础上增加x元后,日均销售利润为y元,
在此情况下的日均销售量为480-40(x-1)=(520-40x)桶.
令520-40x>0,则0y=(520-40x)x-200=-40x2+520x-200=-40(x-6.5)2+1 490,0易知,当x=6.5时,y有最大值.
所以只需将销售单价定为11.5元,就可获得最大利润.
分段函数模型的应用
三
例3
(1)将利润表示为月产量x的函数f(x);
由题意知,总成本为(20 000+100x)元,
(2)当月产量为何值时,公司所获利润最大?最大利润为多少元?(总收益=总成本+利润)
∴当x=300时,f(x)有最大值,为25 000;
当x>400时,f(x)=60 000-100x单调递减,
则f(x)<60 000-100×400=20 000<25 000.
∴当x=300时,f(x)有最大值,为25 000.
即当每月生产300台仪器时,利润最大,最大利润为25 000元.
反思感悟
(1)分段函数的“段”一定要分得合理,不重不漏.
(2)分段函数的定义域为对应每一段自变量取值范围的并集.
(3)分段函数的值域为对应每一段函数值取值范围的并集.分段函数的最值为每一段求函数值的最值(范围),最后比较大小再下结论.
跟踪训练3
某厂生产某种零件,每个零件的成本为40元,出厂单价定为60元,该厂为鼓励销售商订购,决定当一次订购量超过100个时,每多订购一个,订购的全部零件的出厂单价就降低0.02元,但实际出厂单价不能低于51元.
(1)当一次订购量为多少个时,零件的实际出厂单价恰好降为51元?
设每个零件的实际出厂单价恰好降为51元时,一次订购量为x0个,
因此,当一次订购量为550个时,每个零件的实际出厂单价恰好降为51元.
(2)设一次订购量为x个时,零件的实际出厂单价为P元,写出函数P=f(x)的表达式;
当0<x≤100时,P=60;
当x≥550时,P=51,
(3)当销售商一次订购500个零件时,该厂获得的利润是多少元?如果订购1 000个时,利润又是多少元?(工厂售出一个零件的利润=实际出厂单价-成本)
设销售商的一次订购量为x个时,工厂获得的利润为L(x)元,
当x=500时,L(x)=6 000;
当x=1 000时,L(x)=11 000.
因此,当销售商一次订购500个零件时,该厂获得的利润是6 000元;
订购1 000个零件时,利润是11 000元.
课堂
小结
1.知识清单:
(1)一次函数模型的应用.
(2)二次函数模型的应用.
(3)分段函数模型的应用.
2.方法归纳:配方法、判别式法、换元法.
3.常见误区:函数的实际应用问题易忽略函数的定义域.
§3.4 函数的应用(一)
第三章 函数的概念与性质
学习目标
1.初步体会一次函数、二次函数、幂函数、分段函数模型的广泛应用,能运用函数思想处理现实生活中的简单应用问题.(重点)
2.能将实际问题转化为熟悉的模型,建立合适的数学模型解决简单的实际问题.(难点)
导语
2022年是中国共产主义青年团成立100周年.习主席曾寄语青年:“对想做、爱做的事要敢试敢为,努力从无到有、从小到大,把理想变为现实.要敢于做先锋,而不做过客、当看客,让创新成为青春远航的动力,让创业成为青春搏击的能量,让青春年华在为国家、为人民的奉献中焕发出绚丽光彩.”某学校成立了“团员先锋队”去参加建模比赛,你能在我们的日常生活中找到我们所学的函数模型吗?
一、一次函数模型的应用
二、二次函数模型的应用
三、分段函数模型的应用
随堂演练
内容索引
一次函数模型的应用
一
例1
为了发展电信事业,方便用户,电信公司对移动电话采用不同的收费方式,其中所使用的“如意卡”与“便民卡”在某市范围内每月(30天)的通话时间x(分)与通话费用y(元)
的关系如图所示.
(1)分别求出通话费用y1,y2与通话
时间x之间的函数解析式;
由图象可设y1=k1x+30(k1≠0),y2=k2x(k2≠0),
(2)请帮助用户计算在一个月内使用哪种卡便宜.
当x=90时,y1=y2,两种卡收费一致;
当x<90时,y1>y2,使用便民卡便宜;
当x>90时,y1
一次函数模型的特点和求解方法
(1)一次函数模型的突出特点是其图象是一条直线(或一部分).
(2)解一次函数模型时,一般是借助两个点来确定,常用待定系数法.主要步骤是:设元、列式、求解.
跟踪训练1
某公司市场营销人员的个人月收入与其每月的销售量成一次函数关系,其图象如图所示,由图中给出的信息可知,营销人员没有销售量的收入是
A.3 100元 B.3 000元
C.2 900元 D.2 800元
√
设y=kx+b(k≠0),代入(1,8 000)和(2,13 000),
所以y=5 000x+3 000,当x=0时,y=3 000.
二次函数模型的应用
二
例2
设可获得总利润为R(x)万元,
∵R(x)在[0,210]上单调递增,
∴当年产量为210吨时,可获得最大利润1 660万元.
反思感悟
二次函数模型的应用策略
(1)常见问题:有些问题的两变量之间是二次函数关系,如面积问题、利润问题、产量问题、用料问题等,应构建二次函数模型求解.
(2)常用方法:根据实际问题建立二次函数模型解析式后,可利用配方法、判别式法、换元法以及二次函数的图象与单调性等方法求最值,也可以根据函数图象的对称轴与函数定义域的对应区间之间的位置关系讨论求解.
(3)特别注意:取得最值时的自变量的取值与实际意义是否相符.
跟踪训练2
某桶装水经营部每天的房租、人员工资等固定成本为200元,每桶水的进价是5元,销售单价与日均销售量的关系如表所示:
销售单价/元 6 7 8 9 10 11 12
日均销售量/桶 480 440 400 360 320 280 240
请根据以上数据作出分析,这个经营部怎样定价才能获得最大利润?
由表中数据可知,销售单价每增加1元,日均销售量就减少40桶,
设在进价的基础上增加x元后,日均销售利润为y元,
在此情况下的日均销售量为480-40(x-1)=(520-40x)桶.
令520-40x>0,则0
所以只需将销售单价定为11.5元,就可获得最大利润.
分段函数模型的应用
三
例3
(1)将利润表示为月产量x的函数f(x);
由题意知,总成本为(20 000+100x)元,
(2)当月产量为何值时,公司所获利润最大?最大利润为多少元?(总收益=总成本+利润)
∴当x=300时,f(x)有最大值,为25 000;
当x>400时,f(x)=60 000-100x单调递减,
则f(x)<60 000-100×400=20 000<25 000.
∴当x=300时,f(x)有最大值,为25 000.
即当每月生产300台仪器时,利润最大,最大利润为25 000元.
反思感悟
(1)分段函数的“段”一定要分得合理,不重不漏.
(2)分段函数的定义域为对应每一段自变量取值范围的并集.
(3)分段函数的值域为对应每一段函数值取值范围的并集.分段函数的最值为每一段求函数值的最值(范围),最后比较大小再下结论.
跟踪训练3
某厂生产某种零件,每个零件的成本为40元,出厂单价定为60元,该厂为鼓励销售商订购,决定当一次订购量超过100个时,每多订购一个,订购的全部零件的出厂单价就降低0.02元,但实际出厂单价不能低于51元.
(1)当一次订购量为多少个时,零件的实际出厂单价恰好降为51元?
设每个零件的实际出厂单价恰好降为51元时,一次订购量为x0个,
因此,当一次订购量为550个时,每个零件的实际出厂单价恰好降为51元.
(2)设一次订购量为x个时,零件的实际出厂单价为P元,写出函数P=f(x)的表达式;
当0<x≤100时,P=60;
当x≥550时,P=51,
(3)当销售商一次订购500个零件时,该厂获得的利润是多少元?如果订购1 000个时,利润又是多少元?(工厂售出一个零件的利润=实际出厂单价-成本)
设销售商的一次订购量为x个时,工厂获得的利润为L(x)元,
当x=500时,L(x)=6 000;
当x=1 000时,L(x)=11 000.
因此,当销售商一次订购500个零件时,该厂获得的利润是6 000元;
订购1 000个零件时,利润是11 000元.
课堂
小结
1.知识清单:
(1)一次函数模型的应用.
(2)二次函数模型的应用.
(3)分段函数模型的应用.
2.方法归纳:配方法、判别式法、换元法.
3.常见误区:函数的实际应用问题易忽略函数的定义域.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
