第三章 3.1.2函数的表示法(1)高中数学人教A版必修一 课件(共27张PPT)
文档属性
| 名称 | 第三章 3.1.2函数的表示法(1)高中数学人教A版必修一 课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-26 00:00:00 | ||
图片预览







文档简介
(共27张PPT)
3.1.2 函数的表示法(1)
第三章 §3.1 函数的概念及其表示
学习目标
1.了解函数的三种表示方法及各自的优缺点.
2.能用图象法表示函数并能通过函数图象得到函数的值域.(重点)
导语
如果一个人极有才华,我们会用“才高八斗”来形容;如果一个人兼有文武才能,我们会用“出将入相”来形容;如果一个人是稀有而可贵的人才,我们会用“凤毛麟角”来形容;如果一个人品行卓越,天下绝无仅有,我们会用“斗南一人”来形容,那么对于呈现出来的不同函数,是否也会有不同的表示方法呢?让我们一起来探究吧.
一、函数的表示法
二、函数的图象
三、求简单函数的值域
随堂演练
内容索引
函数的表示法
一
问题1 结合初中所学以及上节课的几个问题,你能总结出函数的几种表示方法?
提示 解析法:就是用数学表达式表示两个变量之间的对应关系;列表法:就是列出表格来表示两个变量之间的对应关系;图象法:就是用图象表示两个变量之间的对应关系.
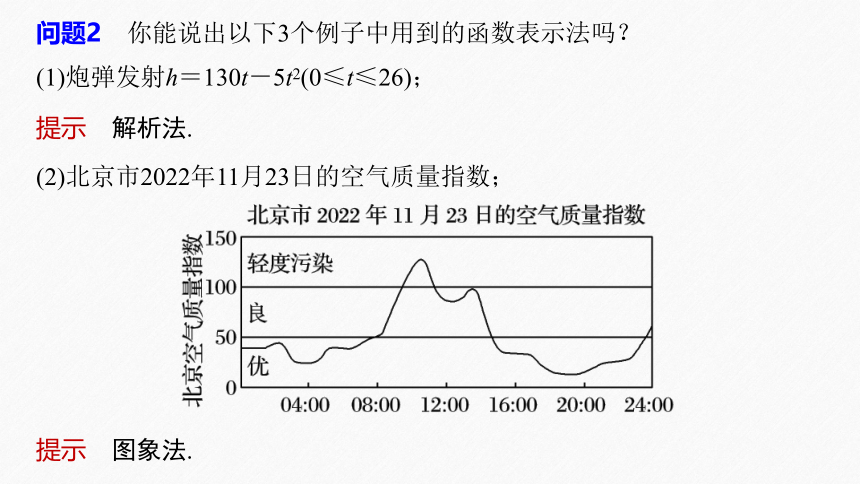
问题2 你能说出以下3个例子中用到的函数表示法吗?
(1)炮弹发射h=130t-5t2(0≤t≤26);
提示 解析法.
(2)北京市2022年11月23日的空气质量指数;
提示 图象法.
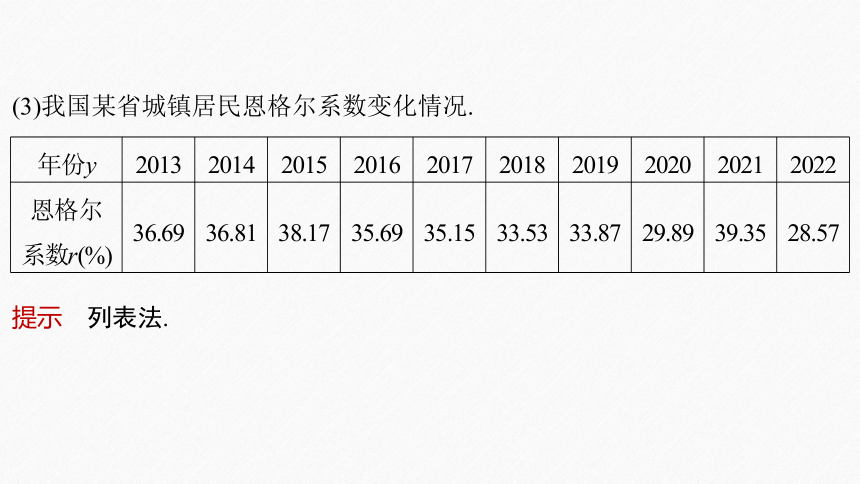
(3)我国某省城镇居民恩格尔系数变化情况.
年份y 2013 2014 2015 2016 2017 2018 2019 2020 2021 2022
恩格尔 系数r(%) 36.69 36.81 38.17 35.69 35.15 33.53 33.87 29.89 39.35 28.57
提示 列表法.
例1
中秋节到了,小明想买几块月饼,已知每块月饼的单价是6元,买x(x∈{1,2,3,4,5,6})块月饼需要y元,试用函数的三种表示方法表示函数y=f(x).
函数的定义域是数集{1,2,3,4,5,6},
用解析法可将函数表示为f(x)=6x,x∈{1,2,3,4,5,6}.
列表法可将函数表示为
月饼数x 1 2 3 4 5 6
钱数y 6 12 18 24 30 36
图象法可将函数表示为
反思感悟
理解函数表示法应注意
(1)列表法、图象法、解析法均是函数的表示法,无论是哪种方式表示函数,都必须满足函数的概念.
(2)列表法更直观形象,图象法从形的角度描述函数,解析法从数的角度描述函数.
(3)函数的三种表示法互相兼容或补充,许多函数是可以用三种方法表示的,但在实际操作中,仍以解析法为主.
跟踪训练1
已知函数f(x)=-x-1,x∈{1,2,3,4},试分别用图象法和列表法表示函数y=f(x).
用图象法表示函数y=f(x),如图所示.
用列表法表示函数y=f(x),如表所示.
x 1 2 3 4
y -2 -3 -4 -5
函数的图象
二
问题3 除了我们所熟悉的“列表、描点、连线”作图,还有哪些作图的方法?
提示 平移变换、对称变换(翻折变换).
知识梳理
1.函数图象的平移变换
(1)左加右减:函数y=f(x)的图象沿x轴方向向左(a>0)或向右(a<0)平移|a|个单位长度得到函数y=f(x+a)的图象.
(2)上加下减:函数y=f(x)的图象沿y轴方向向上(b>0)或向下(b<0)平移|b|个单位长度得到函数y=f(x)+b的图象.
2.函数图象的对称变换
3.函数图象的翻折变换
例2
画出函数y=(x-2)2的图象.
方法一 列表:
x -1 -0.5 0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
y 9 6.25 4 2.25 1 0.25 0 0.25 1 2.25 4 6.25 9
描点、连线,图象如图所示.
方法二 用图象变换法:先作出函数y=x2的图象,然后把它向右平移2个单位长度,就得到函数y=(x-2)2的图象,如图所示.
反思感悟
画函数图象的两种常见方法
(1)描点法:列表、描点、连线.
(2)变换作图法:常用的有平移变换(水平、竖直)、对称变换(翻折)等.
跟踪训练2
√
当x=0时,y=0,排除B.
求简单函数的值域
三
例3
求下列函数的值域:
(1)y=2x+1,x∈{1,2,3,4,5};
∵y=2x+1,且x∈{1,2,3,4,5},
∴y∈{3,5,7,9,11}.
∴函数的值域为{3,5,7,9,11}.
∴函数的值域为[1,+∞).
(3)y=x2-4x+6,x∈[1,5];
配方得y=(x-2)2+2,x∈[1,5],
画出函数的图象如图所示,
由图知,2≤y≤11,
即函数的值域为[2,11].
∴函数的值域为(-∞,3)∪(3,+∞).
反思感悟
求函数值域的方法
(1)观察法:对于一些比较简单的函数,其值域可通过观察得到.
(2)图象法:利用一次函数、二次函数或反比例函数的图象写出函数的值域.
(3)配方法:此方法适用于求“二次函数型”值域,即先将解析式配方,然后利用不等式性质求出其值域.
(4)分离常数法:此方法主要适用于有理分式,即将有理分式转化为“反比例函数型”的形式,便于求值域.
跟踪训练3
求下列函数的值域:
(1)y=-x2-2x+3(-5≤x≤0);
∵x∈[-5,0]在对称轴x=-1的两侧,
∴当x∈[-5,-1]时,抛物线上升,当x∈[-1,0]时,抛物线下降.
∴当x=-5时,ymin=-12,当x=-1时,ymax=4.
∴y=-x2-2x+3(-5≤x≤0)的值域是[-12,4].
课堂
小结
1.知识清单:
(1)函数的表示法.
(2)函数的图象及其应用.
(3)求函数的值域.
2.方法归纳:观察法、配方法、换元法、分离常数法、数形结合法.
3.常见误区:
(1)左右平移忽略加减的是自变量.
(2)求函数值域时忽略函数的定义域.
3.1.2 函数的表示法(1)
第三章 §3.1 函数的概念及其表示
学习目标
1.了解函数的三种表示方法及各自的优缺点.
2.能用图象法表示函数并能通过函数图象得到函数的值域.(重点)
导语
如果一个人极有才华,我们会用“才高八斗”来形容;如果一个人兼有文武才能,我们会用“出将入相”来形容;如果一个人是稀有而可贵的人才,我们会用“凤毛麟角”来形容;如果一个人品行卓越,天下绝无仅有,我们会用“斗南一人”来形容,那么对于呈现出来的不同函数,是否也会有不同的表示方法呢?让我们一起来探究吧.
一、函数的表示法
二、函数的图象
三、求简单函数的值域
随堂演练
内容索引
函数的表示法
一
问题1 结合初中所学以及上节课的几个问题,你能总结出函数的几种表示方法?
提示 解析法:就是用数学表达式表示两个变量之间的对应关系;列表法:就是列出表格来表示两个变量之间的对应关系;图象法:就是用图象表示两个变量之间的对应关系.
问题2 你能说出以下3个例子中用到的函数表示法吗?
(1)炮弹发射h=130t-5t2(0≤t≤26);
提示 解析法.
(2)北京市2022年11月23日的空气质量指数;
提示 图象法.
(3)我国某省城镇居民恩格尔系数变化情况.
年份y 2013 2014 2015 2016 2017 2018 2019 2020 2021 2022
恩格尔 系数r(%) 36.69 36.81 38.17 35.69 35.15 33.53 33.87 29.89 39.35 28.57
提示 列表法.
例1
中秋节到了,小明想买几块月饼,已知每块月饼的单价是6元,买x(x∈{1,2,3,4,5,6})块月饼需要y元,试用函数的三种表示方法表示函数y=f(x).
函数的定义域是数集{1,2,3,4,5,6},
用解析法可将函数表示为f(x)=6x,x∈{1,2,3,4,5,6}.
列表法可将函数表示为
月饼数x 1 2 3 4 5 6
钱数y 6 12 18 24 30 36
图象法可将函数表示为
反思感悟
理解函数表示法应注意
(1)列表法、图象法、解析法均是函数的表示法,无论是哪种方式表示函数,都必须满足函数的概念.
(2)列表法更直观形象,图象法从形的角度描述函数,解析法从数的角度描述函数.
(3)函数的三种表示法互相兼容或补充,许多函数是可以用三种方法表示的,但在实际操作中,仍以解析法为主.
跟踪训练1
已知函数f(x)=-x-1,x∈{1,2,3,4},试分别用图象法和列表法表示函数y=f(x).
用图象法表示函数y=f(x),如图所示.
用列表法表示函数y=f(x),如表所示.
x 1 2 3 4
y -2 -3 -4 -5
函数的图象
二
问题3 除了我们所熟悉的“列表、描点、连线”作图,还有哪些作图的方法?
提示 平移变换、对称变换(翻折变换).
知识梳理
1.函数图象的平移变换
(1)左加右减:函数y=f(x)的图象沿x轴方向向左(a>0)或向右(a<0)平移|a|个单位长度得到函数y=f(x+a)的图象.
(2)上加下减:函数y=f(x)的图象沿y轴方向向上(b>0)或向下(b<0)平移|b|个单位长度得到函数y=f(x)+b的图象.
2.函数图象的对称变换
3.函数图象的翻折变换
例2
画出函数y=(x-2)2的图象.
方法一 列表:
x -1 -0.5 0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
y 9 6.25 4 2.25 1 0.25 0 0.25 1 2.25 4 6.25 9
描点、连线,图象如图所示.
方法二 用图象变换法:先作出函数y=x2的图象,然后把它向右平移2个单位长度,就得到函数y=(x-2)2的图象,如图所示.
反思感悟
画函数图象的两种常见方法
(1)描点法:列表、描点、连线.
(2)变换作图法:常用的有平移变换(水平、竖直)、对称变换(翻折)等.
跟踪训练2
√
当x=0时,y=0,排除B.
求简单函数的值域
三
例3
求下列函数的值域:
(1)y=2x+1,x∈{1,2,3,4,5};
∵y=2x+1,且x∈{1,2,3,4,5},
∴y∈{3,5,7,9,11}.
∴函数的值域为{3,5,7,9,11}.
∴函数的值域为[1,+∞).
(3)y=x2-4x+6,x∈[1,5];
配方得y=(x-2)2+2,x∈[1,5],
画出函数的图象如图所示,
由图知,2≤y≤11,
即函数的值域为[2,11].
∴函数的值域为(-∞,3)∪(3,+∞).
反思感悟
求函数值域的方法
(1)观察法:对于一些比较简单的函数,其值域可通过观察得到.
(2)图象法:利用一次函数、二次函数或反比例函数的图象写出函数的值域.
(3)配方法:此方法适用于求“二次函数型”值域,即先将解析式配方,然后利用不等式性质求出其值域.
(4)分离常数法:此方法主要适用于有理分式,即将有理分式转化为“反比例函数型”的形式,便于求值域.
跟踪训练3
求下列函数的值域:
(1)y=-x2-2x+3(-5≤x≤0);
∵x∈[-5,0]在对称轴x=-1的两侧,
∴当x∈[-5,-1]时,抛物线上升,当x∈[-1,0]时,抛物线下降.
∴当x=-5时,ymin=-12,当x=-1时,ymax=4.
∴y=-x2-2x+3(-5≤x≤0)的值域是[-12,4].
课堂
小结
1.知识清单:
(1)函数的表示法.
(2)函数的图象及其应用.
(3)求函数的值域.
2.方法归纳:观察法、配方法、换元法、分离常数法、数形结合法.
3.常见误区:
(1)左右平移忽略加减的是自变量.
(2)求函数值域时忽略函数的定义域.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
