第三章 3.2.1 单调性与最大(小)值(2)高中数学人教A版必修一课件(共26张PPT)
文档属性
| 名称 | 第三章 3.2.1 单调性与最大(小)值(2)高中数学人教A版必修一课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-26 20:18:06 | ||
图片预览








文档简介
(共26张PPT)
3.2.1 单调性与最大(小)值(2)
第三章 §3.2 函数的基本性质
学习目标
1.了解函数的最大(小)值的概念及其几何意义.
2.能够借助函数图象的直观性得出函数的最值.(重点)
3.会借助函数的单调性求最值.(重点)
4.能够利用函数的单调性解决日常生活中的最值问题.(难点)
导语
108这个数字大家也许并不陌生:《封神榜》里面总共有108位神仙;在《水浒传》中,讲述的是齐聚水泊梁山的108位英雄好汉;在《红楼梦》中,设置了108个章节,等等这些,足以说明108在古人心中认为是数字之最,今天我们也来一次穿越,和古人一起探讨一下我们的函数之最吧!
一、直观感知函数的最大(小)值
二、利用函数的单调性求函数的最值
三、探究生活中的最值问题
随堂演练
内容索引
直观感知函数的最大(小)值
一
问题1 如何求函数f(x)=-x2的最大值.
提示 求函数的最大值可以转化为求函数图象的最高点的纵坐标.
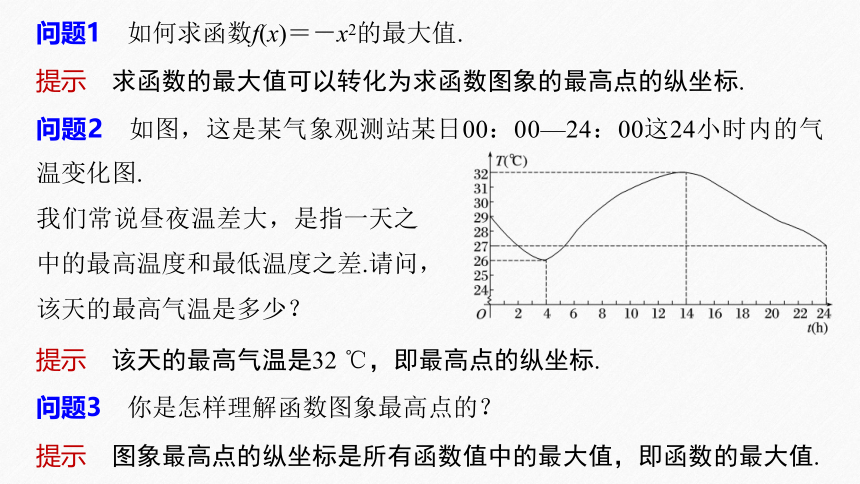
问题2 如图,这是某气象观测站某日00:00—24:00这24小时内的气温变化图.
我们常说昼夜温差大,是指一天之
中的最高温度和最低温度之差.请问,
该天的最高气温是多少?
提示 该天的最高气温是32 ℃,即最高点的纵坐标.
问题3 你是怎样理解函数图象最高点的?
提示 图象最高点的纵坐标是所有函数值中的最大值,即函数的最大值.
知识梳理
函数的最大值
一般地,设函数y=f(x)的定义域为I,如果存在实数M满足:
(1) x∈I,都有f(x) M;
(2) x0∈I,使得 .
那么,我们称M是函数y=f(x)的最大值.
函数的最小值
一般地,设函数y=f(x)的定义域为I,如果存在实数M满足:
(1) x∈I,都有f(x) M;
(2) x0∈I,使得 .
那么,我们称M是函数y=f(x)的最小值.
≤
f(x0)=M
≥
f(x0)=M
注意点:
(1)最大(小)值的几何意义:最高(低)点的纵坐标;
(2)并不是所有的函数都有最大(小)值,比如y=x,x∈R;
(3)一个函数至多有一个最大(小)值;
(4)研究函数最值需先研究函数的定义域和单调性;
(5)对于定义域内的任意x都满足f(x)≤M(f(x)≥M),那么M不一定是函数f(x)的最大(小)值,只有定义域内存在一点x0,使f(x0)=M时,M才是函数的最大(小)值,否则不是.比如f(x)=-x2≤3成立,但3不是f(x)的最大值,0才是它的最大值.
例1
作出f(x)的图象如图.
由图象可知,当x=2时,f(x)取最大值为2;
反思感悟
图象法求函数最值的一般步骤
跟踪训练1
如图是函数f(x)的图象,指出该函数的最大、最小值点及最值.
观察图象知,函数f(x)的最大值点是x=-1,最小值点是x=2,
函数f(x)的最大值是1.5,最小值是-1.
利用函数的单调性求函数的最值
二
问题4 若函数y=f(x)在区间[a,b]上单调递增,则f(x)在区间[a,b]上的最大值与最小值分别是多少?
提示 最大值为f(b),最小值为f(a).
问题5 若f(x)=-x2的定义域为[-1,2],则f(x)的最大值和最小值一定在端点上取到吗?
提示 不一定,需要考虑函数的单调性.
例2
(1)求实数a的值;
(2)判断函数f(x)在(1,+∞)上的单调性,并证明;
函数f(x)在(1,+∞)上单调递增.证明如下:
任取x1,x2∈(1,+∞),不妨设x1∵x1,x2∈(1,+∞)且x1∴x2-x1>0,2x1x2-1>0,x1x2>0,
∴f(x2)-f(x1)>0,即f(x2)>f(x1),
∴f(x)在(1,+∞)上单调递增.
(3)求函数f(x)在[2,3]上的最值.
由(2)知,函数f(x)在[2,3]上单调递增,
反思感悟
(1)利用单调性求最值的一般步骤
①判断函数的定义域.②判断函数的单调性.③利用单调性求出最值.
(2)函数的最值与单调性的关系
①若函数在闭区间[a,b]上单调递减,则f(x)在[a,b]上的最大值为f(a),最小值为f(b).
②若函数在闭区间[a,b]上单调递增,则f(x)在[a,b]上的最大值为f(b),最小值为f(a).
③求最值时一定要注意所给区间的开闭,若是开区间,则不一定有最值.
跟踪训练2
(1)求证:f(x)在[1,+∞)上单调递增;
设1≤x1∵1≤x11,∴x1x2-1>0,
∴f(x)在[1,+∞)上单调递增.
(2)求f(x)在[1,4]上的最大值及最小值.
由(1)可知f(x)在[1,4]上单调递增,
∴当x=1时,f(x)取得最小值,
最小值为f(1)=2,
当x=4时,f(x)取得最大值,
探究生活中的最值问题
三
例3
(1)求出2022年的利润S(万元)关于年产量x(百辆)的函数关系式(利润=销售额-成本);
由题意得当0S(x)=500x-(10x2+100x)-3 000=-10x2+400x-3 000,
当x≥40时,
(2)当2022年产量为多少百辆时,企业所获利润最大?并求出最大利润.
由(1)得当0当x=20时,S(x)max=1 000,
∴当x=100时,S(x)max=1 300,∵1 300>1 000,
∴当x=100时,即2022年产量为1万辆时,企业所获利润最大,且最大利润为1 300万元.
反思感悟
(1)实际问题主要考查二次函数或分段函数的最值问题,以及应用它们解决实际问题的能力.
(2)解应用题的步骤是:
①审清题意,设出未知数;
②建立数学模型,将实际问题转化为数学问题;
③得出结论,回归题意.
跟踪训练3
将进货单价为40元的商品按50元一个出售时,能卖出500个,已知这种商品每涨价1元,其销售量就减少10个,为得到最大利润,售价应为多少元?最大利润为多少?
设售价为x元,利润为y元,单个涨价(x-50)元,销量减少10(x-50)个,
销量为500-10(x-50)=(1 000-10x)个,
则y=(x-40)(1 000-10x)=-10(x-70)2+9 000.
故当x=70时,ymax=9 000.
即售价为70元时,利润最大,最大利润为9 000元.
课堂
小结
1.知识清单:
(1)函数的最大值、最小值定义.
(2)利用函数的单调性求函数最值.
(3)探究生活中的实际问题.
2.方法归纳:配方法、分类讨论法、数形结合法.
3.常见误区:
(1)在利用单调性求最值时,勿忘求函数的定义域.
(2)求含参数的二次函数的最值时,不要忘记按对称轴与区间的位置分类讨论.
3.2.1 单调性与最大(小)值(2)
第三章 §3.2 函数的基本性质
学习目标
1.了解函数的最大(小)值的概念及其几何意义.
2.能够借助函数图象的直观性得出函数的最值.(重点)
3.会借助函数的单调性求最值.(重点)
4.能够利用函数的单调性解决日常生活中的最值问题.(难点)
导语
108这个数字大家也许并不陌生:《封神榜》里面总共有108位神仙;在《水浒传》中,讲述的是齐聚水泊梁山的108位英雄好汉;在《红楼梦》中,设置了108个章节,等等这些,足以说明108在古人心中认为是数字之最,今天我们也来一次穿越,和古人一起探讨一下我们的函数之最吧!
一、直观感知函数的最大(小)值
二、利用函数的单调性求函数的最值
三、探究生活中的最值问题
随堂演练
内容索引
直观感知函数的最大(小)值
一
问题1 如何求函数f(x)=-x2的最大值.
提示 求函数的最大值可以转化为求函数图象的最高点的纵坐标.
问题2 如图,这是某气象观测站某日00:00—24:00这24小时内的气温变化图.
我们常说昼夜温差大,是指一天之
中的最高温度和最低温度之差.请问,
该天的最高气温是多少?
提示 该天的最高气温是32 ℃,即最高点的纵坐标.
问题3 你是怎样理解函数图象最高点的?
提示 图象最高点的纵坐标是所有函数值中的最大值,即函数的最大值.
知识梳理
函数的最大值
一般地,设函数y=f(x)的定义域为I,如果存在实数M满足:
(1) x∈I,都有f(x) M;
(2) x0∈I,使得 .
那么,我们称M是函数y=f(x)的最大值.
函数的最小值
一般地,设函数y=f(x)的定义域为I,如果存在实数M满足:
(1) x∈I,都有f(x) M;
(2) x0∈I,使得 .
那么,我们称M是函数y=f(x)的最小值.
≤
f(x0)=M
≥
f(x0)=M
注意点:
(1)最大(小)值的几何意义:最高(低)点的纵坐标;
(2)并不是所有的函数都有最大(小)值,比如y=x,x∈R;
(3)一个函数至多有一个最大(小)值;
(4)研究函数最值需先研究函数的定义域和单调性;
(5)对于定义域内的任意x都满足f(x)≤M(f(x)≥M),那么M不一定是函数f(x)的最大(小)值,只有定义域内存在一点x0,使f(x0)=M时,M才是函数的最大(小)值,否则不是.比如f(x)=-x2≤3成立,但3不是f(x)的最大值,0才是它的最大值.
例1
作出f(x)的图象如图.
由图象可知,当x=2时,f(x)取最大值为2;
反思感悟
图象法求函数最值的一般步骤
跟踪训练1
如图是函数f(x)的图象,指出该函数的最大、最小值点及最值.
观察图象知,函数f(x)的最大值点是x=-1,最小值点是x=2,
函数f(x)的最大值是1.5,最小值是-1.
利用函数的单调性求函数的最值
二
问题4 若函数y=f(x)在区间[a,b]上单调递增,则f(x)在区间[a,b]上的最大值与最小值分别是多少?
提示 最大值为f(b),最小值为f(a).
问题5 若f(x)=-x2的定义域为[-1,2],则f(x)的最大值和最小值一定在端点上取到吗?
提示 不一定,需要考虑函数的单调性.
例2
(1)求实数a的值;
(2)判断函数f(x)在(1,+∞)上的单调性,并证明;
函数f(x)在(1,+∞)上单调递增.证明如下:
任取x1,x2∈(1,+∞),不妨设x1
∴f(x2)-f(x1)>0,即f(x2)>f(x1),
∴f(x)在(1,+∞)上单调递增.
(3)求函数f(x)在[2,3]上的最值.
由(2)知,函数f(x)在[2,3]上单调递增,
反思感悟
(1)利用单调性求最值的一般步骤
①判断函数的定义域.②判断函数的单调性.③利用单调性求出最值.
(2)函数的最值与单调性的关系
①若函数在闭区间[a,b]上单调递减,则f(x)在[a,b]上的最大值为f(a),最小值为f(b).
②若函数在闭区间[a,b]上单调递增,则f(x)在[a,b]上的最大值为f(b),最小值为f(a).
③求最值时一定要注意所给区间的开闭,若是开区间,则不一定有最值.
跟踪训练2
(1)求证:f(x)在[1,+∞)上单调递增;
设1≤x1
∴f(x)在[1,+∞)上单调递增.
(2)求f(x)在[1,4]上的最大值及最小值.
由(1)可知f(x)在[1,4]上单调递增,
∴当x=1时,f(x)取得最小值,
最小值为f(1)=2,
当x=4时,f(x)取得最大值,
探究生活中的最值问题
三
例3
(1)求出2022年的利润S(万元)关于年产量x(百辆)的函数关系式(利润=销售额-成本);
由题意得当0
当x≥40时,
(2)当2022年产量为多少百辆时,企业所获利润最大?并求出最大利润.
由(1)得当0
∴当x=100时,S(x)max=1 300,∵1 300>1 000,
∴当x=100时,即2022年产量为1万辆时,企业所获利润最大,且最大利润为1 300万元.
反思感悟
(1)实际问题主要考查二次函数或分段函数的最值问题,以及应用它们解决实际问题的能力.
(2)解应用题的步骤是:
①审清题意,设出未知数;
②建立数学模型,将实际问题转化为数学问题;
③得出结论,回归题意.
跟踪训练3
将进货单价为40元的商品按50元一个出售时,能卖出500个,已知这种商品每涨价1元,其销售量就减少10个,为得到最大利润,售价应为多少元?最大利润为多少?
设售价为x元,利润为y元,单个涨价(x-50)元,销量减少10(x-50)个,
销量为500-10(x-50)=(1 000-10x)个,
则y=(x-40)(1 000-10x)=-10(x-70)2+9 000.
故当x=70时,ymax=9 000.
即售价为70元时,利润最大,最大利润为9 000元.
课堂
小结
1.知识清单:
(1)函数的最大值、最小值定义.
(2)利用函数的单调性求函数最值.
(3)探究生活中的实际问题.
2.方法归纳:配方法、分类讨论法、数形结合法.
3.常见误区:
(1)在利用单调性求最值时,勿忘求函数的定义域.
(2)求含参数的二次函数的最值时,不要忘记按对称轴与区间的位置分类讨论.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
