第三章 3.2.1 单调性与最大(小)值(1)高中数学人教A版必修一 课件(共25张PPT)
文档属性
| 名称 | 第三章 3.2.1 单调性与最大(小)值(1)高中数学人教A版必修一 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-26 20:18:41 | ||
图片预览






文档简介
(共25张PPT)
3.2.1 单调性与最大(小)值(1)
第三章 §3.2 函数的基本性质
学习目标
1.能借助函数图象理解函数在某区间上单调递增、单调递减和增函数、减函数的概念.
2.理解函数在某区间上具有(严格的)单调性和单调区间的概念.(重点)
3.能运用定义法证明函数的单调性.(难点)
导语
海宁潮,又名钱塘潮,自古称之为“天下奇观”.“八月十八潮,壮观天下无”.海宁潮是一个壮观无比的自然动态奇观,当江潮从东面来时,似一条银线,“则玉城雪岭际天而来,大声如雷霆,震撼激射,吞天沃日,势极雄豪.”潮起潮落,牵动了无数人的心.如何用函数形式表示起与落呢?本节课我们就来研究一下!
一、直观感知函数的单调性
二、利用定义证明函数的单调性
三、函数单调性的简单应用
随堂演练
内容索引
直观感知函数的单调性
一
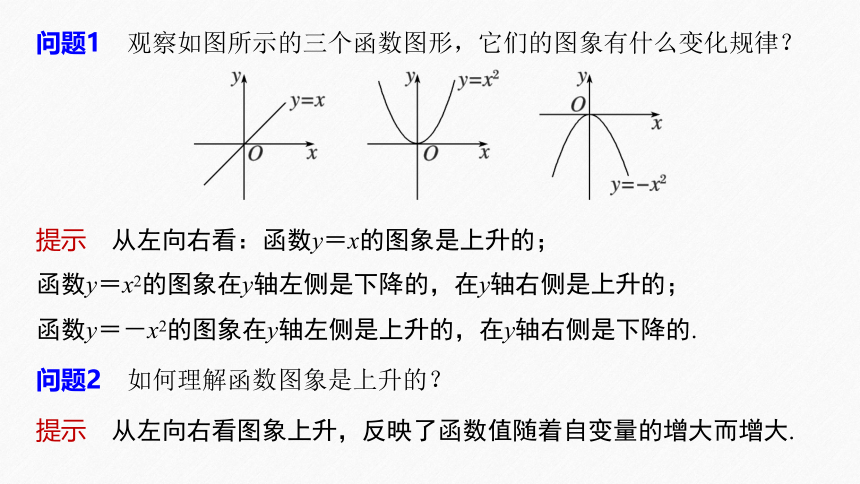
问题1 观察如图所示的三个函数图形,它们的图象有什么变化规律?
提示 从左向右看:函数y=x的图象是上升的;
函数y=x2的图象在y轴左侧是下降的,在y轴右侧是上升的;
函数y=-x2的图象在y轴左侧是上升的,在y轴右侧是下降的.
问题2 如何理解函数图象是上升的?
提示 从左向右看图象上升,反映了函数值随着自变量的增大而增大.
知识梳理
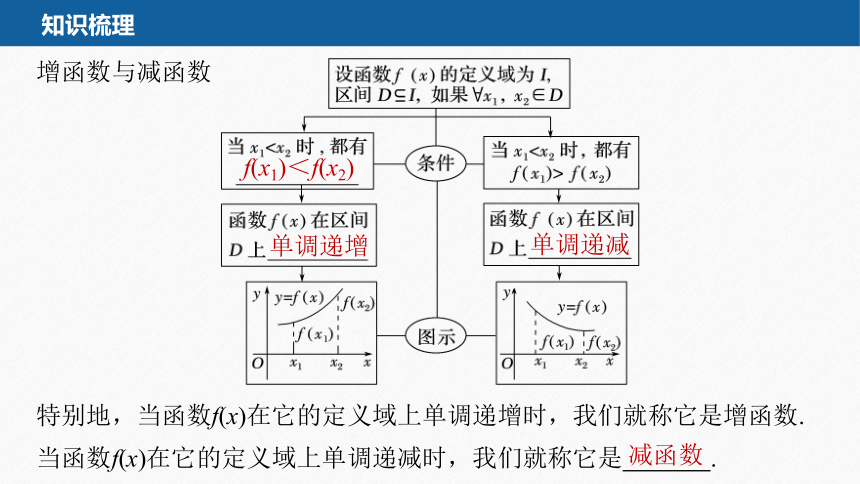
增函数与减函数
特别地,当函数f(x)在它的定义域上单调递增时,我们就称它是增函数.
当函数f(x)在它的定义域上单调递减时,我们就称它是 .
f(x1)<f(x2)
单调递增
单调递减
减函数
注意点:
(1)区间D可以是整个定义域I,也可以是定义域的真子集;
(2)同区间性,即x1,x2∈D;
(3)任意性,即不可以用区间D上的特殊值代替;
(4)有序性,即要规定x1,x2的大小;
(5)“单调递增(递减)”“x1,x2的大小”“f(x1)与f(x2)的大小”知二求一;
(6)单调递增(递减)是函数的局部性质,增(减)函数是函数的整体性质.
例1
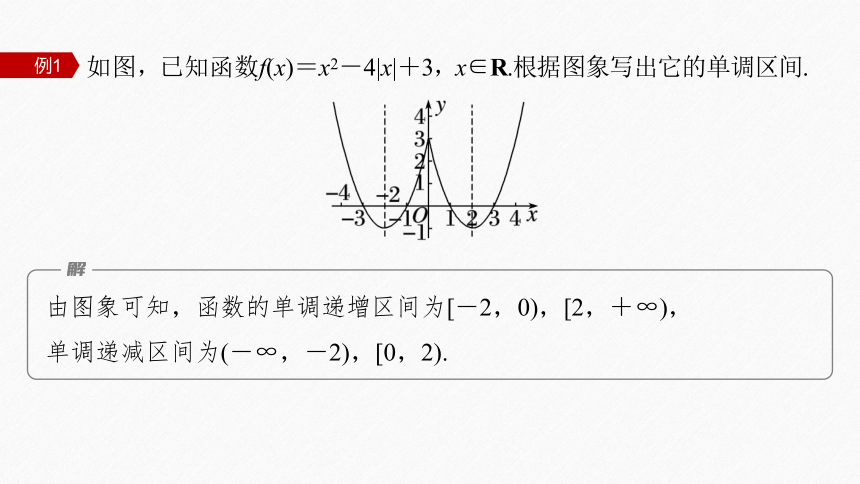
如图,已知函数f(x)=x2-4|x|+3,x∈R.根据图象写出它的单调区间.
由图象可知,函数的单调递增区间为[-2,0),[2,+∞),
单调递减区间为(-∞,-2),[0,2).
反思感悟
(1)求函数单调区间时,若所给函数是常见的一次函数、二次函数、反比例函数等,可根据其单调性写出函数的单调区间.
(2)若函数不是上述常见函数且函数图象容易作出,可作出其图象,根据图象写出其单调区间.
(3)一个函数有多个单调区间时,区间不能用“∪”连接,而要用“和”或“,”连接.
跟踪训练1
画出函数y=|x|(x-2)的图象,并指出函数的单调区间.
函数的图象如图实线部分所示.
由函数的图象知,函数的单调递增区间为(-∞,0]和[1,+∞),单调递减区间为(0,1).
利用定义证明函数的单调性
二
例2
x1,x2∈(2,+∞),且x1因为2所以x2-x1>0,x2+x1>0,x1+2>0,x1-2>0,x2+2>0,x2-2>0,
所以f(x1)-f(x2)>0,即f(x1)>f(x2).
x1,x2∈(2,+∞),且x1因为2所以x2-x1>0,x2+x1>0,x1+2>0,x1-2>0,x2+2>0,x2-2>0,
当a>0时,f(x1)-f(x2)>0,即f(x1)>f(x2).
当a<0时,f(x1)-f(x2)<0,即f(x1)反思感悟
利用定义证明函数单调性的步骤
(1)取值(定大小):设x1,x2是所证区间内的任意两个值,且x1(2)作差(变形):作差f(x1)-f(x2),并通过因式分解、通分、配方、有理化等手段,转化为积或商等易判断符号的关系式.
(3)定号:确定f(x1)-f(x2)的符号,当符号不确定时,进行分类讨论.
(4)结论:根据定义写出结论.
跟踪训练2
x1,x2∈(-∞,0),且x1由题设可得,x1-x2<0,x1x2>0,
所以f(x1)-f(x2)<0,即f(x1)函数单调性的简单应用
三
例3
(1)若函数f(x)=-x2-2(a+1)x+3在区间(-∞,3]上单调递增,则实数a的取值范围是____________.
(-∞,-4]
f(x)=-x2-2(a+1)x+3=-(x+a+1)2+(a+1)2+3.
因此函数的单调递增区间为(-∞,-a-1],
由f(x)在(-∞,3]上单调递增知3≤-a-1,
解得a≤-4,即实数a的取值范围为(-∞,-4].
(2)已知函数y=f(x)是(-∞,+∞)上的增函数,且f(2x-3)>f(5x-6),则实数x的取值范围为__________.
(-∞,1)
∵f(x)在(-∞,+∞)上是增函数,
且f(2x-3)>f(5x-6),
∴2x-3>5x-6,即x<1.
∴实数x的取值范围为(-∞,1).
延伸探究
1.在本例(1)中,若函数f(x)=-x2-2(a+1)x+3的单调递增区间是(-∞,3],则实数a的值为_____.
-4
f(x)=-x2-2(a+1)x+3=-(x+a+1)2+(a+1)2+3.
因此函数的单调递增区间为(-∞,-a-1],
由题意得-a-1=3,a=-4.
2.若本例(2)的函数f(x)是定义在(0,+∞)上的减函数,求x的取值范围.
反思感悟
由函数单调性求参数范围的处理方法
(1)由函数解析式求参数
①若为二次函数,判断开口方向与对称轴,利用单调性确定参数满足的条件.
②若为一次函数,由一次项系数的正负决定单调性.
③若为复合函数y=|f(x)|或y=f(|x|),利用数形结合,探求参数满足的条件.
(2)当函数f(x)的解析式未知或非常复杂时,欲求解不等式,可以依据函数单调性的定义和性质,将符号“f”去掉,列出关于自变量的不等式(组),然后求解,此时注意函数的定义域.
跟踪训练3
[4,8)
因为f(x)是R上的增函数,
解得4≤a<8.
课堂
小结
1.知识清单:
(1)增函数、减函数的定义.
(2)利用定义证明函数的单调性.
(3)函数单调性的简单应用.
2.方法归纳:定义法、作差法、分类讨论法、数形结合法.
3.常见误区:
(1)函数的单调区间不能用并集.
(2)利用函数的单调性求参数的取值范围忽略函数的定义域.
3.2.1 单调性与最大(小)值(1)
第三章 §3.2 函数的基本性质
学习目标
1.能借助函数图象理解函数在某区间上单调递增、单调递减和增函数、减函数的概念.
2.理解函数在某区间上具有(严格的)单调性和单调区间的概念.(重点)
3.能运用定义法证明函数的单调性.(难点)
导语
海宁潮,又名钱塘潮,自古称之为“天下奇观”.“八月十八潮,壮观天下无”.海宁潮是一个壮观无比的自然动态奇观,当江潮从东面来时,似一条银线,“则玉城雪岭际天而来,大声如雷霆,震撼激射,吞天沃日,势极雄豪.”潮起潮落,牵动了无数人的心.如何用函数形式表示起与落呢?本节课我们就来研究一下!
一、直观感知函数的单调性
二、利用定义证明函数的单调性
三、函数单调性的简单应用
随堂演练
内容索引
直观感知函数的单调性
一
问题1 观察如图所示的三个函数图形,它们的图象有什么变化规律?
提示 从左向右看:函数y=x的图象是上升的;
函数y=x2的图象在y轴左侧是下降的,在y轴右侧是上升的;
函数y=-x2的图象在y轴左侧是上升的,在y轴右侧是下降的.
问题2 如何理解函数图象是上升的?
提示 从左向右看图象上升,反映了函数值随着自变量的增大而增大.
知识梳理
增函数与减函数
特别地,当函数f(x)在它的定义域上单调递增时,我们就称它是增函数.
当函数f(x)在它的定义域上单调递减时,我们就称它是 .
f(x1)<f(x2)
单调递增
单调递减
减函数
注意点:
(1)区间D可以是整个定义域I,也可以是定义域的真子集;
(2)同区间性,即x1,x2∈D;
(3)任意性,即不可以用区间D上的特殊值代替;
(4)有序性,即要规定x1,x2的大小;
(5)“单调递增(递减)”“x1,x2的大小”“f(x1)与f(x2)的大小”知二求一;
(6)单调递增(递减)是函数的局部性质,增(减)函数是函数的整体性质.
例1
如图,已知函数f(x)=x2-4|x|+3,x∈R.根据图象写出它的单调区间.
由图象可知,函数的单调递增区间为[-2,0),[2,+∞),
单调递减区间为(-∞,-2),[0,2).
反思感悟
(1)求函数单调区间时,若所给函数是常见的一次函数、二次函数、反比例函数等,可根据其单调性写出函数的单调区间.
(2)若函数不是上述常见函数且函数图象容易作出,可作出其图象,根据图象写出其单调区间.
(3)一个函数有多个单调区间时,区间不能用“∪”连接,而要用“和”或“,”连接.
跟踪训练1
画出函数y=|x|(x-2)的图象,并指出函数的单调区间.
函数的图象如图实线部分所示.
由函数的图象知,函数的单调递增区间为(-∞,0]和[1,+∞),单调递减区间为(0,1).
利用定义证明函数的单调性
二
例2
x1,x2∈(2,+∞),且x1
所以f(x1)-f(x2)>0,即f(x1)>f(x2).
x1,x2∈(2,+∞),且x1
当a>0时,f(x1)-f(x2)>0,即f(x1)>f(x2).
当a<0时,f(x1)-f(x2)<0,即f(x1)
利用定义证明函数单调性的步骤
(1)取值(定大小):设x1,x2是所证区间内的任意两个值,且x1
(3)定号:确定f(x1)-f(x2)的符号,当符号不确定时,进行分类讨论.
(4)结论:根据定义写出结论.
跟踪训练2
x1,x2∈(-∞,0),且x1
所以f(x1)-f(x2)<0,即f(x1)
三
例3
(1)若函数f(x)=-x2-2(a+1)x+3在区间(-∞,3]上单调递增,则实数a的取值范围是____________.
(-∞,-4]
f(x)=-x2-2(a+1)x+3=-(x+a+1)2+(a+1)2+3.
因此函数的单调递增区间为(-∞,-a-1],
由f(x)在(-∞,3]上单调递增知3≤-a-1,
解得a≤-4,即实数a的取值范围为(-∞,-4].
(2)已知函数y=f(x)是(-∞,+∞)上的增函数,且f(2x-3)>f(5x-6),则实数x的取值范围为__________.
(-∞,1)
∵f(x)在(-∞,+∞)上是增函数,
且f(2x-3)>f(5x-6),
∴2x-3>5x-6,即x<1.
∴实数x的取值范围为(-∞,1).
延伸探究
1.在本例(1)中,若函数f(x)=-x2-2(a+1)x+3的单调递增区间是(-∞,3],则实数a的值为_____.
-4
f(x)=-x2-2(a+1)x+3=-(x+a+1)2+(a+1)2+3.
因此函数的单调递增区间为(-∞,-a-1],
由题意得-a-1=3,a=-4.
2.若本例(2)的函数f(x)是定义在(0,+∞)上的减函数,求x的取值范围.
反思感悟
由函数单调性求参数范围的处理方法
(1)由函数解析式求参数
①若为二次函数,判断开口方向与对称轴,利用单调性确定参数满足的条件.
②若为一次函数,由一次项系数的正负决定单调性.
③若为复合函数y=|f(x)|或y=f(|x|),利用数形结合,探求参数满足的条件.
(2)当函数f(x)的解析式未知或非常复杂时,欲求解不等式,可以依据函数单调性的定义和性质,将符号“f”去掉,列出关于自变量的不等式(组),然后求解,此时注意函数的定义域.
跟踪训练3
[4,8)
因为f(x)是R上的增函数,
解得4≤a<8.
课堂
小结
1.知识清单:
(1)增函数、减函数的定义.
(2)利用定义证明函数的单调性.
(3)函数单调性的简单应用.
2.方法归纳:定义法、作差法、分类讨论法、数形结合法.
3.常见误区:
(1)函数的单调区间不能用并集.
(2)利用函数的单调性求参数的取值范围忽略函数的定义域.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
