湖南省部分名校联盟2023届高三5月冲刺压轴大联考数学试题(无答案)
文档属性
| 名称 | 湖南省部分名校联盟2023届高三5月冲刺压轴大联考数学试题(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 330.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-26 21:27:59 | ||
图片预览


文档简介
湖南省部分名校联盟2023届高三5月冲刺压轴大联考数学试题
学校:___________姓名:___________班级:___________考号:___________
一、未知
1.已知集合,则集合中元素个数为( )
A.1 B.2 C.2023 D.2024
2.已知复数是纯虚数,则实数的值为( )
A. B. C. D.
3.阅读下列材料:有理数都能表示成(,且与互质)的形式,从而有理数集,任何有理数都可以化为有限小数或无限循环小数;反之,任一有限小数或者无限循环小数也可以化为的形式,从而是有理数.例如:.循环小数化成分数为( )
A. B. C. D.
4.在中,已知,向量在向量上的投影向量为,点是边上靠近的三等分点,则( )
A.3 B.6 C.7 D.9
5.已知是直线的倾斜角,则的值为( )
A. B. C. D.
6.学校校园从教室到寝室的一排路灯共12盏,按照规定,如果两端有坏了的路灯或者中间同时坏了相邻的两盏或两盏以上的路灯,就必须马上维修,已知这排路灯坏了3盏,则这排路灯必须马上维修的概率为( )
A. B. C. D.
7.定义:与圆锥的底面和各母线均相切的球,称为圆锥的内切球,此圆锥称为球的外切圆锥.已知某圆锥的内切球半径等于1,则该圆锥体积的最小值为( )
A. B. C. D.
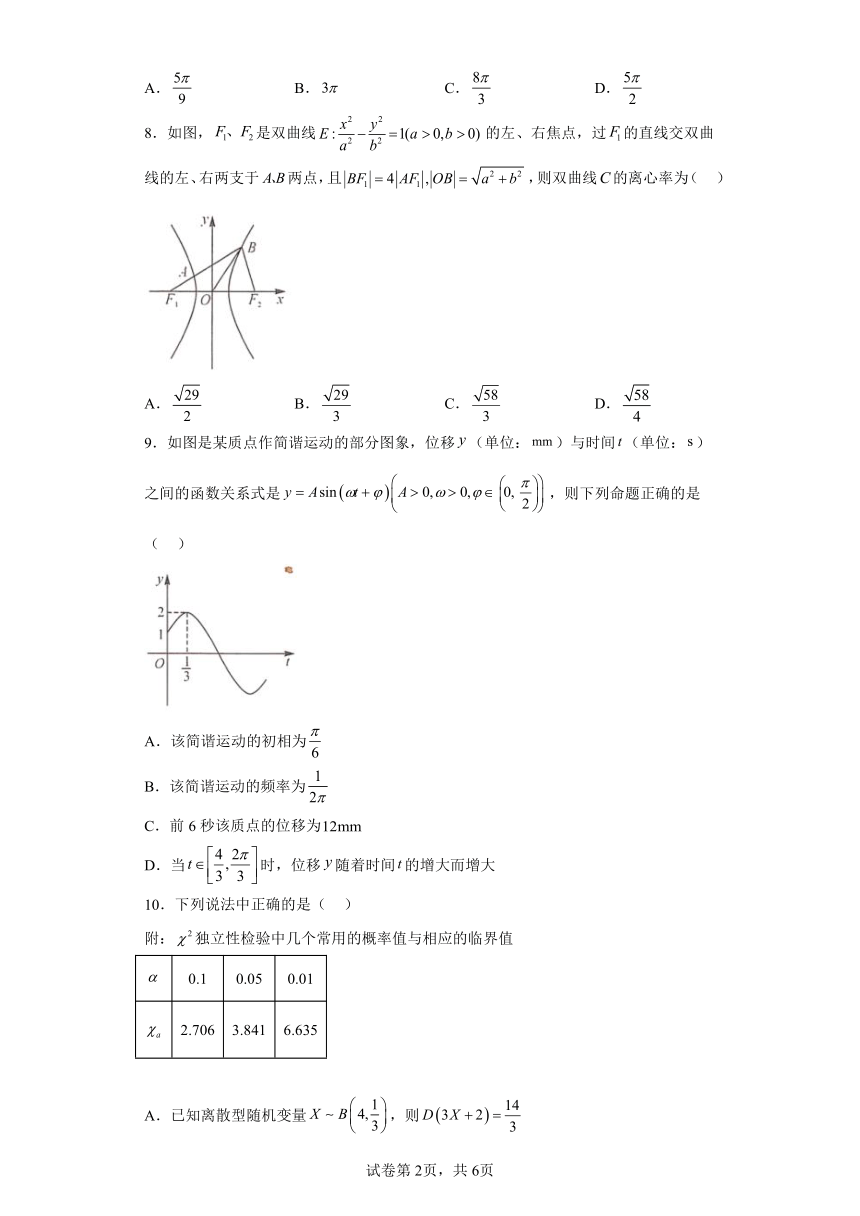
8.如图,是双曲线的左、右焦点,过的直线交双曲线的左、右两支于两点,且,则双曲线的离心率为( )
A. B. C. D.
9.如图是某质点作简谐运动的部分图象,位移(单位:)与时间(单位:)之间的函数关系式是,则下列命题正确的是( )
A.该简谐运动的初相为
B.该简谐运动的频率为
C.前6秒该质点的位移为
D.当时,位移随着时间的增大而增大
10.下列说法中正确的是( )
附:独立性检验中几个常用的概率值与相应的临界值
0.1 0.05 0.01
2.706 3.841 6.635
A.已知离散型随机变量,则
B.一组数据148,149,154,155,155,156,157,158,159,161的第75百分位数为158
C.若,则事件与相互独立
D.根据分类变量与的观测数据,计算得到,依据的独立性检验可得:变量与独立,这个结论错误的概率不超过0.05
11.已知圆,直线,则( )
A.直线恒过定点
B.直线能表示平面直角坐标系内每一条直线
C.对任意实数,直线都与圆相交
D.直线被圆截得的弦长的最小值为
12.在棱长为1的正方体中,为正方体表面上的动点,为线段上的动点,若直线与的夹角为,则下列说法正确的是( )
A.点的轨迹确定的图形是平面图形
B.点的轨迹长度为
C.的最小值为
D.当点在侧面上时,的最小值为1
13.2023年5月湖南省部分高三学生参加高三第一次模拟大联考,假如联考的数学成绩服从正态分布,其总体密度函数为:,且.若参加此次联考的学生共有80000人,则数学成绩超过100分的人数大约为__________.
14.若函数是奇函数,则曲线在点处的切线方程为__________.
15.已知抛物线的焦点为,过点且斜率为正的直线与抛物线相交于两点,且.若过点的圆与直线相切于第一象限的点,则的值为__________.
16.已知函数,对于任意,都有,则实数的取值范围为__________.
17.已知数列的首项,且满足.
(1)求证:数列是等差数列;
(2)若数列满足,求数列的前项和.
18.在中,分别是角所对的边,向量,且.
(1)求角的大小;
(2)若,求外接圆半径的最小值.
19.如图,在三棱台中,,.
(1)证明:平面平面;
(2)设是的中点,求平面与平面夹角的余弦值.
20.华为云服务是华为公司在ICT领域通过30多年的技术攻坚和经验积累,将产品解决方案开放给用户,为用户提供集个人数据同步、云相册、手机找回等多种基础云功能,旨在为消费者提供一站式易用、快捷、智能、安全的个人数据管理服务.华为云服务采用按需使用、按需付费的一站式IT计算资源租用服务.据调查,在某一地区自2016年至2022年以来,7年的使用用户数如下表所示:(x表示年度,2016年度记为1,2017年度记为2,…,依次类推,2022年度记为7;y表示该年度使用的用户数,单位:千户).
x 1 2 3 4 5 6 7
y 7 9 21 36 66 100 198
根据以上数据,绘制了如图所示的散点图.
(1)根据散点图判断,在这7年内,与(c,d均为大于零的常数)哪一个适宜作为该地区华为云用户数(千户)关于年度的回归方程类型?(给出判断即可,不必说明理由);并根据表中数据,求关于的经验回归方程,估计2023年度用户数(保留到千户位);
(2)该地区按用户使用华为云服务的时间,从高到低评为三个等第的星级,其中连续使用华为云5年以上的用户评为“五星用户”,三年以上五年以下的用户评为“三星用户”,其它用户评为“星级用户”,每位用户年服务费按星级从高到低依次为50元、70元、90元.为了拓展用户数量,该地区今年推出一项用户星级升级的抽奖活动,每位用户可抽奖两次,每次抽奖有的概率升两级,有的概率升一级,还有的概率不升级,最高升为“五星用户”.现某家庭有2位华为云用户,其中甲是“三星用户”,乙是“星级用户”,求今年该家庭支付华为云服务费的分布列与数学期望.
参考数据:
62.43 1.54 2548 50.12 3.47
其中.
参考公式:经验回归直线方程中斜率与截距的最小二乘法估计公式分别为.
21.已知双曲线的一个焦点到其一条渐近线的距离等于其离心率.
(1)求双曲线的方程;
(2)若直线与椭圆相切,且与双曲线的左、右支分别交于两点,与双曲线的渐近线分别交于两点.为坐标原点,记的面积分别为,当时,求直线的方程.
22.已知函数与分别是与的导函数.
(1)证明:当时,方程在上有且仅有一个实数根;
(2)若对任意的,不等式恒成立,求实数的取值范围.
试卷第1页,共3页
试卷第1页,共3页
学校:___________姓名:___________班级:___________考号:___________
一、未知
1.已知集合,则集合中元素个数为( )
A.1 B.2 C.2023 D.2024
2.已知复数是纯虚数,则实数的值为( )
A. B. C. D.
3.阅读下列材料:有理数都能表示成(,且与互质)的形式,从而有理数集,任何有理数都可以化为有限小数或无限循环小数;反之,任一有限小数或者无限循环小数也可以化为的形式,从而是有理数.例如:.循环小数化成分数为( )
A. B. C. D.
4.在中,已知,向量在向量上的投影向量为,点是边上靠近的三等分点,则( )
A.3 B.6 C.7 D.9
5.已知是直线的倾斜角,则的值为( )
A. B. C. D.
6.学校校园从教室到寝室的一排路灯共12盏,按照规定,如果两端有坏了的路灯或者中间同时坏了相邻的两盏或两盏以上的路灯,就必须马上维修,已知这排路灯坏了3盏,则这排路灯必须马上维修的概率为( )
A. B. C. D.
7.定义:与圆锥的底面和各母线均相切的球,称为圆锥的内切球,此圆锥称为球的外切圆锥.已知某圆锥的内切球半径等于1,则该圆锥体积的最小值为( )
A. B. C. D.
8.如图,是双曲线的左、右焦点,过的直线交双曲线的左、右两支于两点,且,则双曲线的离心率为( )
A. B. C. D.
9.如图是某质点作简谐运动的部分图象,位移(单位:)与时间(单位:)之间的函数关系式是,则下列命题正确的是( )
A.该简谐运动的初相为
B.该简谐运动的频率为
C.前6秒该质点的位移为
D.当时,位移随着时间的增大而增大
10.下列说法中正确的是( )
附:独立性检验中几个常用的概率值与相应的临界值
0.1 0.05 0.01
2.706 3.841 6.635
A.已知离散型随机变量,则
B.一组数据148,149,154,155,155,156,157,158,159,161的第75百分位数为158
C.若,则事件与相互独立
D.根据分类变量与的观测数据,计算得到,依据的独立性检验可得:变量与独立,这个结论错误的概率不超过0.05
11.已知圆,直线,则( )
A.直线恒过定点
B.直线能表示平面直角坐标系内每一条直线
C.对任意实数,直线都与圆相交
D.直线被圆截得的弦长的最小值为
12.在棱长为1的正方体中,为正方体表面上的动点,为线段上的动点,若直线与的夹角为,则下列说法正确的是( )
A.点的轨迹确定的图形是平面图形
B.点的轨迹长度为
C.的最小值为
D.当点在侧面上时,的最小值为1
13.2023年5月湖南省部分高三学生参加高三第一次模拟大联考,假如联考的数学成绩服从正态分布,其总体密度函数为:,且.若参加此次联考的学生共有80000人,则数学成绩超过100分的人数大约为__________.
14.若函数是奇函数,则曲线在点处的切线方程为__________.
15.已知抛物线的焦点为,过点且斜率为正的直线与抛物线相交于两点,且.若过点的圆与直线相切于第一象限的点,则的值为__________.
16.已知函数,对于任意,都有,则实数的取值范围为__________.
17.已知数列的首项,且满足.
(1)求证:数列是等差数列;
(2)若数列满足,求数列的前项和.
18.在中,分别是角所对的边,向量,且.
(1)求角的大小;
(2)若,求外接圆半径的最小值.
19.如图,在三棱台中,,.
(1)证明:平面平面;
(2)设是的中点,求平面与平面夹角的余弦值.
20.华为云服务是华为公司在ICT领域通过30多年的技术攻坚和经验积累,将产品解决方案开放给用户,为用户提供集个人数据同步、云相册、手机找回等多种基础云功能,旨在为消费者提供一站式易用、快捷、智能、安全的个人数据管理服务.华为云服务采用按需使用、按需付费的一站式IT计算资源租用服务.据调查,在某一地区自2016年至2022年以来,7年的使用用户数如下表所示:(x表示年度,2016年度记为1,2017年度记为2,…,依次类推,2022年度记为7;y表示该年度使用的用户数,单位:千户).
x 1 2 3 4 5 6 7
y 7 9 21 36 66 100 198
根据以上数据,绘制了如图所示的散点图.
(1)根据散点图判断,在这7年内,与(c,d均为大于零的常数)哪一个适宜作为该地区华为云用户数(千户)关于年度的回归方程类型?(给出判断即可,不必说明理由);并根据表中数据,求关于的经验回归方程,估计2023年度用户数(保留到千户位);
(2)该地区按用户使用华为云服务的时间,从高到低评为三个等第的星级,其中连续使用华为云5年以上的用户评为“五星用户”,三年以上五年以下的用户评为“三星用户”,其它用户评为“星级用户”,每位用户年服务费按星级从高到低依次为50元、70元、90元.为了拓展用户数量,该地区今年推出一项用户星级升级的抽奖活动,每位用户可抽奖两次,每次抽奖有的概率升两级,有的概率升一级,还有的概率不升级,最高升为“五星用户”.现某家庭有2位华为云用户,其中甲是“三星用户”,乙是“星级用户”,求今年该家庭支付华为云服务费的分布列与数学期望.
参考数据:
62.43 1.54 2548 50.12 3.47
其中.
参考公式:经验回归直线方程中斜率与截距的最小二乘法估计公式分别为.
21.已知双曲线的一个焦点到其一条渐近线的距离等于其离心率.
(1)求双曲线的方程;
(2)若直线与椭圆相切,且与双曲线的左、右支分别交于两点,与双曲线的渐近线分别交于两点.为坐标原点,记的面积分别为,当时,求直线的方程.
22.已知函数与分别是与的导函数.
(1)证明:当时,方程在上有且仅有一个实数根;
(2)若对任意的,不等式恒成立,求实数的取值范围.
试卷第1页,共3页
试卷第1页,共3页
同课章节目录
