第四章 §4.2 4.2.2 指数函数的图象和性质(二)-高中数学人教A版必修一 课件(共30张PPT)
文档属性
| 名称 | 第四章 §4.2 4.2.2 指数函数的图象和性质(二)-高中数学人教A版必修一 课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-27 06:04:07 | ||
图片预览




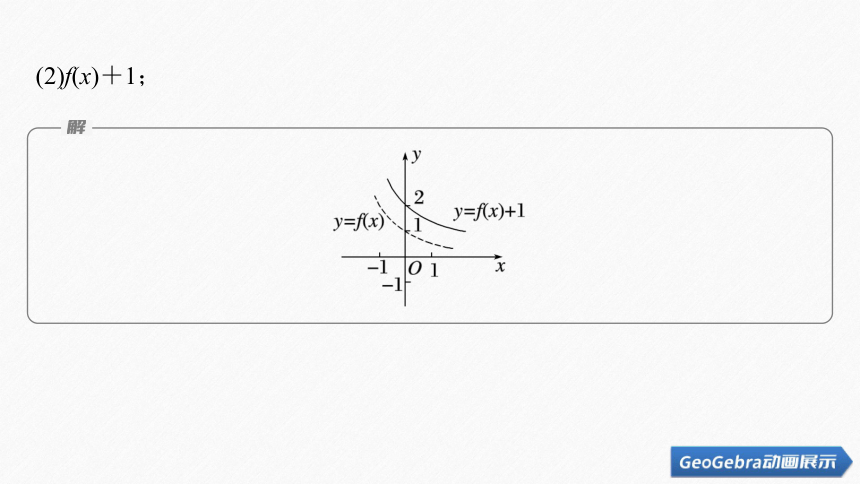
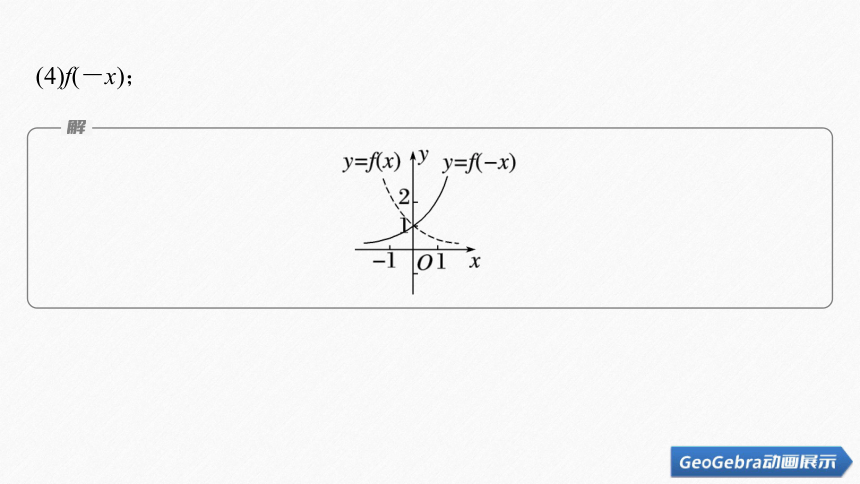

文档简介
(共30张PPT)
4.2.2 指数函数的图象和性质(二)
第四章 §4.2 指数函数
学习目标
1.掌握与指数函数有关的图象变换.(重难点)
2.能求给定区间的值域问题.
3.能解决指数函数简单的实际应用问题.
一、与指数函数有关的图象变换
二、定区间的值域问题
三、指数函数的实际应用
随堂演练
内容索引
与指数函数有关的图象变换
一
例1
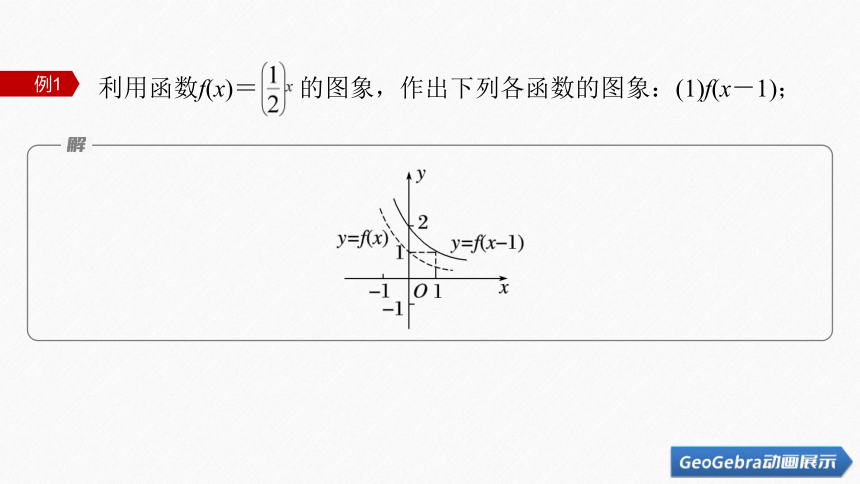
利用函数f(x)= 的图象,作出下列各函数的图象:(1)f(x-1);
(2)f(x)+1;
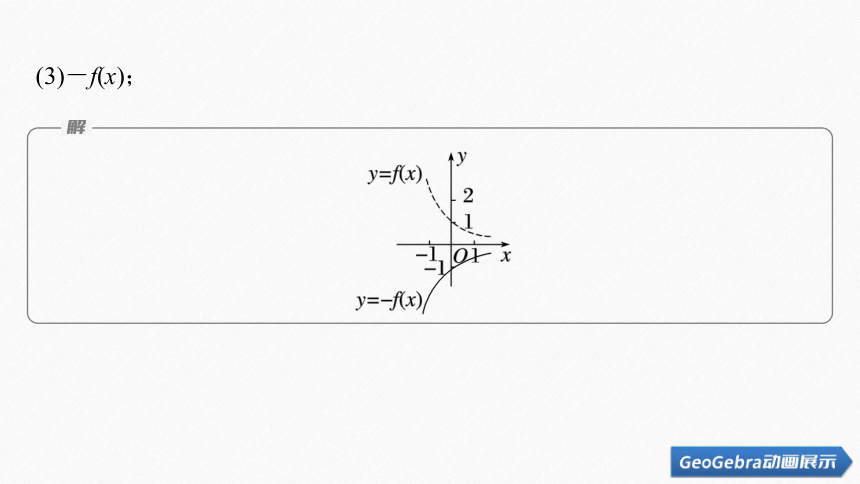
(3)-f(x);
(4)f(-x);
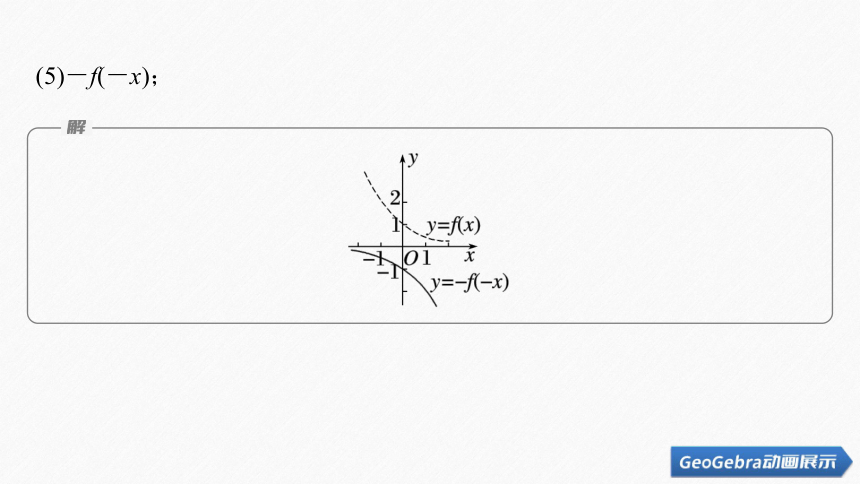
(5)-f(-x);
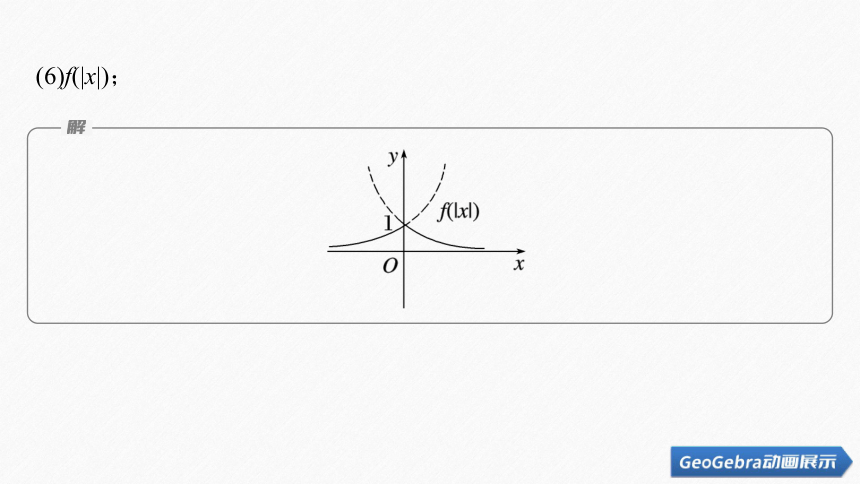
(6)f(|x|);
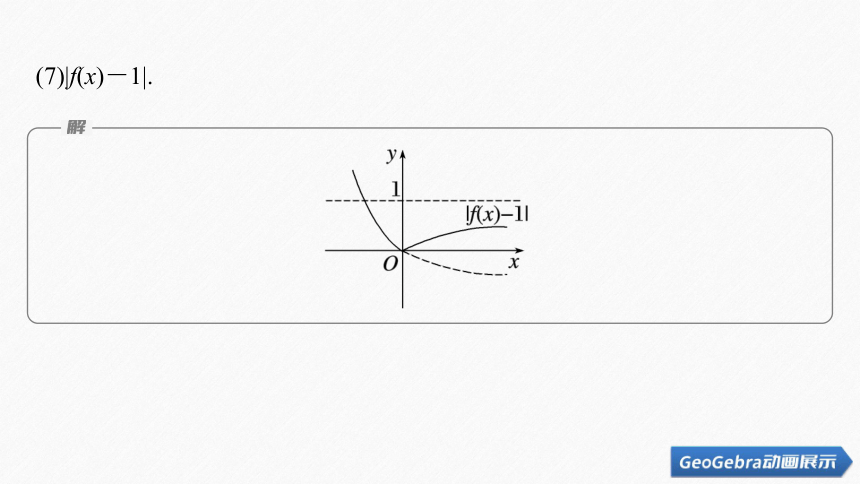
(7)|f(x)-1|.
反思感悟
图形变换
反思感悟
反思感悟
跟踪训练1
已知函数y=3x的图象,怎样变换得到y= +2的图象?并画出相应图象.
再向左平移1个单位长度就得到函数y=3-(x+1)的图象,
定区间的值域问题
二
例2
√
x2+1≤4-2x,解得-3≤x≤1,所以2-3≤2x≤2,
反思感悟
关于定区间上的值域问题
(1)求定区间上的值域关键是确定函数的单调性,如果底数中含字母,则分a>1,0(2)特别地,如果是最大值与最小值的和,则不需要讨论,因为无论单调递增还是单调递减,最值总在端点处取到.
跟踪训练2
函数f(x)=3-x在[-2,1]上的值域是
√
指数函数的实际应用
三
例3
某林区2022年木材蓄积量为200万立方米,由于采取了封山育林、严禁采伐等措施,使木材蓄积量的年平均递增率能达到5%.
(1)若经过x年后,该林区的木材蓄积量为y万立方米,求y=f(x)的表达式,并求此函数的定义域;
现有木材蓄积量为200万立方米,经过1年后木材蓄积量为200+200×5%=200(1+5%),
经过2年后木材蓄积量为200(1+5%)+200(1+5%)×5%=200×(1+5%)2,…,
∴经过x年后木材蓄积量为200(1+5%)x.
∴y=f(x)=200(1+5%)x,x∈N*.
(2)求经过多少年后,林区的木材蓄积量能达到300万立方米.
作函数y=f(x)=200(1+5%)x(x≥0)的图象如图所示.
x 0 1 2 3 …
y 200 210 220.5 231.5 …
作直线y=300与函数y=200(1+5%)x的图象交于A点,则A(x0,300),A点的横坐标x0的值就是函数值y=300时(木材蓄积量为300万立方米时)所经过的时间x的值.
∵8反思感悟
解决有关增长率问题的关键和措施
(1)解决这类问题的关键是理解增长(衰减)率的意义:增长(衰减)率是所研究的对象在“单位时间”内比它在“前单位时间”内的增长(衰减)率,切记并不总是只和开始单位时间内的比较.
(2)分析具体问题时,应严格计算并写出前3~4个单位时间的具体值,通过观察、归纳出规律后,再抽象为数学问题,最后求解数学问题即可.
反思感悟
(3)在实际问题中,有关人口增长、银行复利、细胞分裂等增长率问题常可以用指数函数模型表示,通常可以表示为y=N(1+p)x(其中N为基础数,p为增长率,x为时间)的形式.
跟踪训练3
酒驾是严重危害交通安全的违法行为,为了保障安全,根据国家有关规定:100毫升血液中酒精含量达到20~79 mg的驾驶员即为酒后驾车,80 mg及以上认定为醉酒驾车.某驾驶员喝了一定量的酒后,其血液中酒精含量上升到了0.6 mg/ml,如果停止饮酒后,他的血液中的酒精会以每小时25%的速度减少,那么他至少要经过几个小时后才能驾车
A.6 B.5 C.4 D.3
√
设至少经过x个小时后才能驾驶汽车,
结合选项可知,至少经过4个小时后才能驾驶汽车.
课堂
小结
1.知识清单:
(1)与指数函数有关的图象变换.
(2)给定区间的值域.
(3)指数型函数的实际应用.
2.方法归纳:数形结合.
3.常见误区:混淆|f(x)|与f(|x|)两种变换.
4.2.2 指数函数的图象和性质(二)
第四章 §4.2 指数函数
学习目标
1.掌握与指数函数有关的图象变换.(重难点)
2.能求给定区间的值域问题.
3.能解决指数函数简单的实际应用问题.
一、与指数函数有关的图象变换
二、定区间的值域问题
三、指数函数的实际应用
随堂演练
内容索引
与指数函数有关的图象变换
一
例1
利用函数f(x)= 的图象,作出下列各函数的图象:(1)f(x-1);
(2)f(x)+1;
(3)-f(x);
(4)f(-x);
(5)-f(-x);
(6)f(|x|);
(7)|f(x)-1|.
反思感悟
图形变换
反思感悟
反思感悟
跟踪训练1
已知函数y=3x的图象,怎样变换得到y= +2的图象?并画出相应图象.
再向左平移1个单位长度就得到函数y=3-(x+1)的图象,
定区间的值域问题
二
例2
√
x2+1≤4-2x,解得-3≤x≤1,所以2-3≤2x≤2,
反思感悟
关于定区间上的值域问题
(1)求定区间上的值域关键是确定函数的单调性,如果底数中含字母,则分a>1,0
跟踪训练2
函数f(x)=3-x在[-2,1]上的值域是
√
指数函数的实际应用
三
例3
某林区2022年木材蓄积量为200万立方米,由于采取了封山育林、严禁采伐等措施,使木材蓄积量的年平均递增率能达到5%.
(1)若经过x年后,该林区的木材蓄积量为y万立方米,求y=f(x)的表达式,并求此函数的定义域;
现有木材蓄积量为200万立方米,经过1年后木材蓄积量为200+200×5%=200(1+5%),
经过2年后木材蓄积量为200(1+5%)+200(1+5%)×5%=200×(1+5%)2,…,
∴经过x年后木材蓄积量为200(1+5%)x.
∴y=f(x)=200(1+5%)x,x∈N*.
(2)求经过多少年后,林区的木材蓄积量能达到300万立方米.
作函数y=f(x)=200(1+5%)x(x≥0)的图象如图所示.
x 0 1 2 3 …
y 200 210 220.5 231.5 …
作直线y=300与函数y=200(1+5%)x的图象交于A点,则A(x0,300),A点的横坐标x0的值就是函数值y=300时(木材蓄积量为300万立方米时)所经过的时间x的值.
∵8
解决有关增长率问题的关键和措施
(1)解决这类问题的关键是理解增长(衰减)率的意义:增长(衰减)率是所研究的对象在“单位时间”内比它在“前单位时间”内的增长(衰减)率,切记并不总是只和开始单位时间内的比较.
(2)分析具体问题时,应严格计算并写出前3~4个单位时间的具体值,通过观察、归纳出规律后,再抽象为数学问题,最后求解数学问题即可.
反思感悟
(3)在实际问题中,有关人口增长、银行复利、细胞分裂等增长率问题常可以用指数函数模型表示,通常可以表示为y=N(1+p)x(其中N为基础数,p为增长率,x为时间)的形式.
跟踪训练3
酒驾是严重危害交通安全的违法行为,为了保障安全,根据国家有关规定:100毫升血液中酒精含量达到20~79 mg的驾驶员即为酒后驾车,80 mg及以上认定为醉酒驾车.某驾驶员喝了一定量的酒后,其血液中酒精含量上升到了0.6 mg/ml,如果停止饮酒后,他的血液中的酒精会以每小时25%的速度减少,那么他至少要经过几个小时后才能驾车
A.6 B.5 C.4 D.3
√
设至少经过x个小时后才能驾驶汽车,
结合选项可知,至少经过4个小时后才能驾驶汽车.
课堂
小结
1.知识清单:
(1)与指数函数有关的图象变换.
(2)给定区间的值域.
(3)指数型函数的实际应用.
2.方法归纳:数形结合.
3.常见误区:混淆|f(x)|与f(|x|)两种变换.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
