第四章 §4.4 4.4.2 对数函数的图象和性质(一)-高中数学人教A版必修一 课件(共34张PPT)
文档属性
| 名称 | 第四章 §4.4 4.4.2 对数函数的图象和性质(一)-高中数学人教A版必修一 课件(共34张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-27 06:07:28 | ||
图片预览








文档简介
(共34张PPT)
4.4.2 对数函数的图象和性质(一)
第四章 §4.4 对数函数
学习目标
1.会类比指数函数研究对数函数的性质,初步掌握对数函数的图象和性质.(重点)
2.掌握对数函数的图象和性质的简单应用.(重难点)
导语
同学们,还记得我们是如何研究指数函数的吗?实际上,研究对数函数的思路和研究指数函数的思路是一致的,我们可以用类比的方法来研究对数函数.
一、对数函数的图象和性质
二、利用单调性比较对数值的大小
三、利用单调性解对数不等式
随堂演练
内容索引
对数函数的图象和性质
一
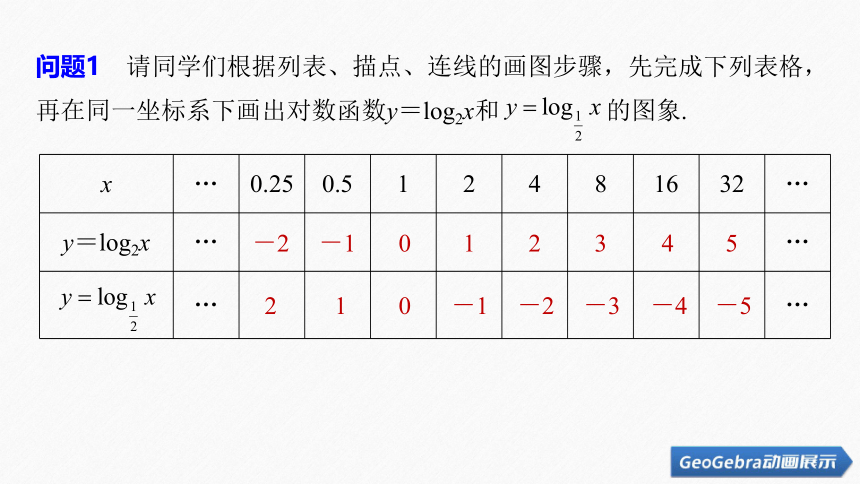
问题1 请同学们根据列表、描点、连线的画图步骤,先完成下列表格,再在同一坐标系下画出对数函数y=log2x和 的图象.
x … 0.25 0.5 1 2 4 8 16 32 …
y=log2x … …
… …
-2
-1
0
1
2
3
4
5
2
1
0
-1
-2
-3
-4
-5
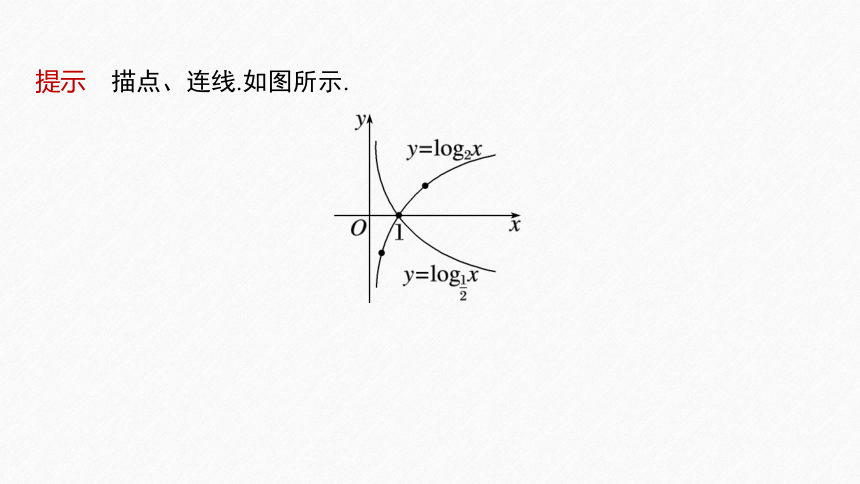
提示 描点、连线.如图所示.
问题2 通过观察函数y=log2x和 的图象,分析性质,并完成下表:
函数 y=log2x
定义域
值域
单调性
最值
奇偶性
(0,+∞)
(0,+∞)
R
R
增函数
减函数
无最值
无最值
非奇非偶函数
非奇非偶函数
特殊点
y的变换情况 当01时,_____ 当0当x>1时,_____
对称性 y=log2x和 的图象关于x轴对称
(1,0)
(1,0)
y<0
y>0
y>0
y<0
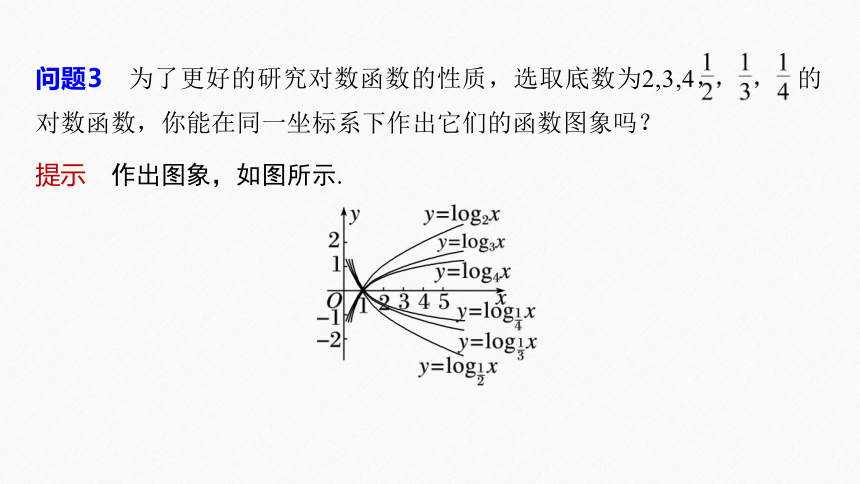
问题3 为了更好的研究对数函数的性质,选取底数为2,3,4, 的对数函数,你能在同一坐标系下作出它们的函数图象吗?
提示 作出图象,如图所示.
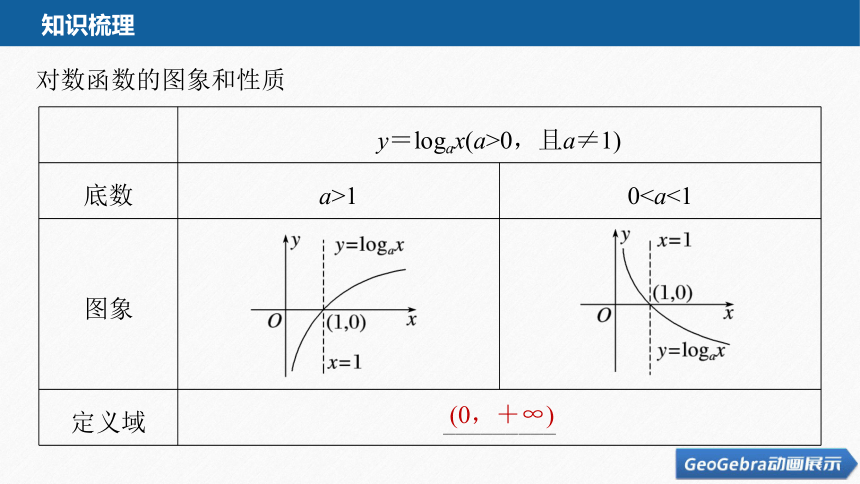
知识梳理
对数函数的图象和性质
y=logax(a>0,且a≠1)
底数 a>1 0图象
定义域 _________
(0,+∞)
值域 R
单调性 在(0,+∞)上是增函数 在(0,+∞)上是减函数
最值 _______________
奇偶性 _____________
共点性 过定点 ,即x=1时,y=0
函数值特点 x∈(0,1)时,y∈ ; x∈[1,+∞)时,y∈_________ x∈(0,1)时,y∈ ; x∈[1,+∞)时,y∈________
对称性 函数y=logax与 的图象关于 对称
无最大、最小值
非奇非偶函数
(1,0)
(-∞,0)
[0,+∞)
(0,+∞)
(-∞,0]
x轴
注意点:
(1)函数图象只出现在y轴右侧.
(2)对任意底数a,当x=1时,y=0,故过定点(1,0).
(3)当0(4)当a>1时,底数越大,图象越靠近x轴.
(5)任意底数互为倒数的两个对数函数的图象关于x轴对称.
例1
(1)如图,若C1,C2分别为函数y=logax和y=logbx的图象,则
A.0B.0C.a>b>1
D.b>a>1
√
作直线y=1,则直线与C1,C2的交点的横坐标分别为a,b,易知0(2)若函数y=loga(x+b)+c(a>0,且a≠1)的图象恒过定点(3,2),则实数b=_____,c=____.
-2
2
∵函数的图象恒过定点(3,2),
∴将(3,2)代入y=loga(x+b)+c,
得2=loga(3+b)+c.
又当a>0,且a≠1时,loga1=0恒成立,
∴c=2,3+b=1,∴b=-2,c=2.
反思感悟
对数函数图象的特点
(1)研究对数函数图象时,应注意底数a的范围,若判断底数不同的对数函数的图象,可在x轴上方画一水平直线,自左向右底数增大.
(2)对数型函数过定点问题,可令真数为1,求出定点.
跟踪训练1
(1)(多选)已知a>0,且a≠1,则函数y=ax与y=logax的图象可能是
√
√
若0若a>1,则函数y=ax的图象单调递增且过点(0,1),而函数y=logax的图象单调递增且过点(1,0),只有A,C中图象符合.
(2)函数f(x)=loga(2x-5)的图象恒过定点_______.
(3,0)
由2x-5=1得x=3,则f(3)=loga1=0.
即函数f(x)恒过定点(3,0).
利用单调性比较对数值的大小
二
例2
比较下列各组中两个值的大小:
(1)log31.9,log32;
因为y=log3x在(0,+∞)上单调递增,1.9<2,
所以log31.9(2)log23,log0.32;
因为log23>log21=0,log0.32所以log23>log0.32.
(3)logaπ,loga3.14(a>0,且a≠1);
当a>1时,函数y=logax在(0,+∞)上单调递增,
则有logaπ>loga3.14;
当0则有logaπ综上所述,当a>1时,logaπ>loga3.14;
当0(4)log50.4,log60.4.
在同一直角坐标系中,作出y=log5x,y=log6x的图象,再作出直线x=0.4(图略),
观察图象可得log50.4反思感悟
比较对数值大小常用的四种方法
(1)同底数的利用对数函数的单调性.
(2)同真数的利用对数函数的图象或用换底公式转化.
(3)底数和真数都不同,找中间量.
(4)若底数为同一参数,则根据底数对对数函数单调性的影响,对底数进行分类讨论.
跟踪训练2
比较大小:
(1)loga5.1,loga5.9(a>0,且a≠1);
当a>1时,y=logax在(0,+∞)上是增函数,
又5.1<5.9,所以loga5.1当0又5.1<5.9,所以loga5.1>loga5.9.
综上,当a>1时,loga5.1当0loga5.9.
利用单调性解对数不等式
三
例3
解下列关于x的不等式:
(1) ;
所以原不等式的解集为{x|0(2)loga(2x-5)>loga(x-1);
综上所述,当a>1时,原不等式的解集为{x|x>4};
反思感悟
对数不等式的三种考查类型及解法
(1)形如logax>logab的不等式,借助y=logax的单调性求解,如果a的取值不确定,需分a>1与0(2)形如logax>b的不等式,应将b化为以a为底数的对数式的形式(b=logaab),再借助y=logax的单调性求解.
(3)形如logf(x)a>logg(x)a(f(x),g(x)>0且不等于1,a>0)的不等式,可利用换底公式化为同底的对数进行求解,或利用函数图象求解.
跟踪训练3
(1)求满足不等式log3x<1的x的取值范围;
∵log3x<1=log33,
且函数y=log3x在(0,+∞)上为增函数,
∴x的取值范围是{x|0(2)已知log0.7(2x)∵函数y=log0.7x在(0,+∞)上为减函数,
∴x的取值范围是(1,+∞).
课堂
小结
1.知识清单:
(1)对数函数的图象及性质.
(2)利用对数函数的图象及性质比较大小.
(3)利用单调性解对数不等式.
2.方法归纳:分类讨论、数形结合法.
3.常见误区:作对数函数图象时易忽视底数a>1与0
4.4.2 对数函数的图象和性质(一)
第四章 §4.4 对数函数
学习目标
1.会类比指数函数研究对数函数的性质,初步掌握对数函数的图象和性质.(重点)
2.掌握对数函数的图象和性质的简单应用.(重难点)
导语
同学们,还记得我们是如何研究指数函数的吗?实际上,研究对数函数的思路和研究指数函数的思路是一致的,我们可以用类比的方法来研究对数函数.
一、对数函数的图象和性质
二、利用单调性比较对数值的大小
三、利用单调性解对数不等式
随堂演练
内容索引
对数函数的图象和性质
一
问题1 请同学们根据列表、描点、连线的画图步骤,先完成下列表格,再在同一坐标系下画出对数函数y=log2x和 的图象.
x … 0.25 0.5 1 2 4 8 16 32 …
y=log2x … …
… …
-2
-1
0
1
2
3
4
5
2
1
0
-1
-2
-3
-4
-5
提示 描点、连线.如图所示.
问题2 通过观察函数y=log2x和 的图象,分析性质,并完成下表:
函数 y=log2x
定义域
值域
单调性
最值
奇偶性
(0,+∞)
(0,+∞)
R
R
增函数
减函数
无最值
无最值
非奇非偶函数
非奇非偶函数
特殊点
y的变换情况 当0
对称性 y=log2x和 的图象关于x轴对称
(1,0)
(1,0)
y<0
y>0
y>0
y<0
问题3 为了更好的研究对数函数的性质,选取底数为2,3,4, 的对数函数,你能在同一坐标系下作出它们的函数图象吗?
提示 作出图象,如图所示.
知识梳理
对数函数的图象和性质
y=logax(a>0,且a≠1)
底数 a>1 0
定义域 _________
(0,+∞)
值域 R
单调性 在(0,+∞)上是增函数 在(0,+∞)上是减函数
最值 _______________
奇偶性 _____________
共点性 过定点 ,即x=1时,y=0
函数值特点 x∈(0,1)时,y∈ ; x∈[1,+∞)时,y∈_________ x∈(0,1)时,y∈ ; x∈[1,+∞)时,y∈________
对称性 函数y=logax与 的图象关于 对称
无最大、最小值
非奇非偶函数
(1,0)
(-∞,0)
[0,+∞)
(0,+∞)
(-∞,0]
x轴
注意点:
(1)函数图象只出现在y轴右侧.
(2)对任意底数a,当x=1时,y=0,故过定点(1,0).
(3)当0
(5)任意底数互为倒数的两个对数函数的图象关于x轴对称.
例1
(1)如图,若C1,C2分别为函数y=logax和y=logbx的图象,则
A.0
D.b>a>1
√
作直线y=1,则直线与C1,C2的交点的横坐标分别为a,b,易知0
-2
2
∵函数的图象恒过定点(3,2),
∴将(3,2)代入y=loga(x+b)+c,
得2=loga(3+b)+c.
又当a>0,且a≠1时,loga1=0恒成立,
∴c=2,3+b=1,∴b=-2,c=2.
反思感悟
对数函数图象的特点
(1)研究对数函数图象时,应注意底数a的范围,若判断底数不同的对数函数的图象,可在x轴上方画一水平直线,自左向右底数增大.
(2)对数型函数过定点问题,可令真数为1,求出定点.
跟踪训练1
(1)(多选)已知a>0,且a≠1,则函数y=ax与y=logax的图象可能是
√
√
若0
(2)函数f(x)=loga(2x-5)的图象恒过定点_______.
(3,0)
由2x-5=1得x=3,则f(3)=loga1=0.
即函数f(x)恒过定点(3,0).
利用单调性比较对数值的大小
二
例2
比较下列各组中两个值的大小:
(1)log31.9,log32;
因为y=log3x在(0,+∞)上单调递增,1.9<2,
所以log31.9
因为log23>log21=0,log0.32
(3)logaπ,loga3.14(a>0,且a≠1);
当a>1时,函数y=logax在(0,+∞)上单调递增,
则有logaπ>loga3.14;
当0
当0
在同一直角坐标系中,作出y=log5x,y=log6x的图象,再作出直线x=0.4(图略),
观察图象可得log50.4
比较对数值大小常用的四种方法
(1)同底数的利用对数函数的单调性.
(2)同真数的利用对数函数的图象或用换底公式转化.
(3)底数和真数都不同,找中间量.
(4)若底数为同一参数,则根据底数对对数函数单调性的影响,对底数进行分类讨论.
跟踪训练2
比较大小:
(1)loga5.1,loga5.9(a>0,且a≠1);
当a>1时,y=logax在(0,+∞)上是增函数,
又5.1<5.9,所以loga5.1
综上,当a>1时,loga5.1
利用单调性解对数不等式
三
例3
解下列关于x的不等式:
(1) ;
所以原不等式的解集为{x|0
综上所述,当a>1时,原不等式的解集为{x|x>4};
反思感悟
对数不等式的三种考查类型及解法
(1)形如logax>logab的不等式,借助y=logax的单调性求解,如果a的取值不确定,需分a>1与0
(3)形如logf(x)a>logg(x)a(f(x),g(x)>0且不等于1,a>0)的不等式,可利用换底公式化为同底的对数进行求解,或利用函数图象求解.
跟踪训练3
(1)求满足不等式log3x<1的x的取值范围;
∵log3x<1=log33,
且函数y=log3x在(0,+∞)上为增函数,
∴x的取值范围是{x|0
∴x的取值范围是(1,+∞).
课堂
小结
1.知识清单:
(1)对数函数的图象及性质.
(2)利用对数函数的图象及性质比较大小.
(3)利用单调性解对数不等式.
2.方法归纳:分类讨论、数形结合法.
3.常见误区:作对数函数图象时易忽视底数a>1与0
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
