第五章 §5.1 5.1.1 任意角-高中数学人教A版必修一 课件(共48张PPT)
文档属性
| 名称 | 第五章 §5.1 5.1.1 任意角-高中数学人教A版必修一 课件(共48张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-27 06:11:50 | ||
图片预览











文档简介
(共48张PPT)
5.1.1 任意角
第五章 §5.1 任意角和弧度制
1.了解任意角的概念,区分正角、负角与零角.
2.了解象限角的概念,理解并掌握终边相同的角的概念,能写出终边相同的角
所组成的集合.(重点)
3.利用象限角和终边相同的角的概念解决简单的问题.(难点)
学习目标
导语
2022年2月8日,北京冬奥会自由式滑雪女子大跳台决赛展开争夺,谷爱凌在前两轮成绩落后的情况下,第三轮超越自己做出
了此前从未做出过的向左偏轴转体1 620,得到94.50分的高分,也凭借总成绩188.25分夺得了这枚宝贵的金牌!我们该怎样理解向左偏轴转体1 620呢?这和角度是分不开的,为了研究这个问题,我们开始今天的新课.
一、任意角
二、象限角
三、终边相同的角
随堂演练
四、区域角的表示
内容索引
任意角
一
问题1 在初中是如何定义角的?角的范围是多少?
提示 角可以看成一条射线绕着它的端点旋转所成的图形,角的范围是0°~360°.
1.角的概念及其表示
角可以看成一条 绕着它的端点 所成的 .如图,
(1)始边:射线的 位置OA;
终边:射线的 位置OB;
顶点:射线的端点O.
(2)记法:图中的角α可记为“角α”或“∠α”或“∠AOB”.
知识梳理
射线
旋转
图形
起始
终止
名称 定义 图示
正角 一条射线绕其端点按 方向旋转形成的角
负角 一条射线绕其端点按 方向旋转形成的角
零角 一条射线 做任何旋转形成的角
2.任意角:我们把角的概念推广到了任意角,包括正角、负角和零角.
逆时针
顺时针
没有
3.角的相等
如果角α和角β的旋转方向相同且旋转量相等,那么就称 .
4.角的加法
设α,β是任意两个角,把角α的终边旋转角β,这时终边所对应的角是
.
5.相反角:把射线OA绕端点O按不同方向旋转相同的量所成的两个角
叫做互为 ,角α的相反角记为 ,α-β=α+ .
α=β
α+β
相反角
-α
(-β)
如图,射线OA先绕端点O逆时针方向旋转60°到OB处,再按顺时针方向旋转820°至OC处,则β= .
例1
-40°
∠AOC=60°+(-820°)=-760°,
β=-760°+720°=-40°.
弄清角的始边与终边及旋转方向与大小.逆时针旋转形成一个正角,顺时针旋转形成一个负角.正角与负角是表示具有相反意义的旋转量,它的正负规定纯属习惯,就好像正数和负数的规定一样.
反思感悟
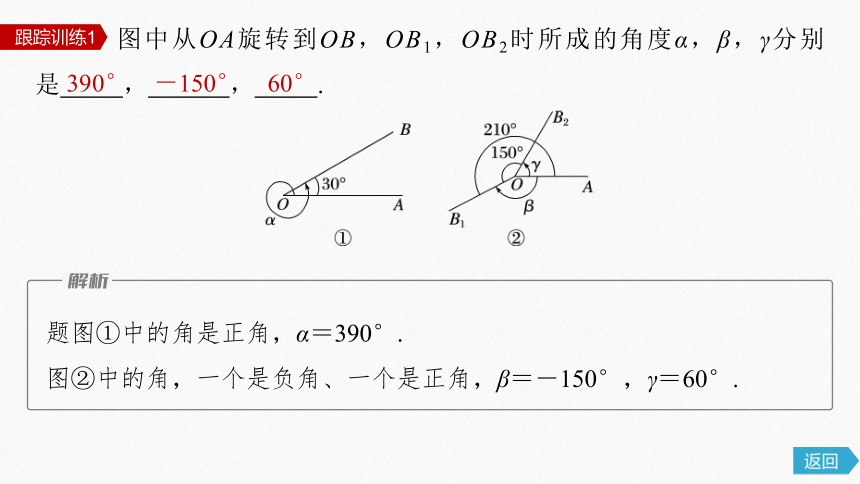
图中从OA旋转到OB,OB1,OB2时所成的角度α,β,γ分别是 , , .
跟踪训练1
390°
-150°
60°
题图①中的角是正角,α=390°.
图②中的角,一个是负角、一个是正角,β=-150°,γ=60°.
象限角
二
问题2 初中所学的0°~360°角可以怎样分类?
提示 锐角、直角、钝角、平角和周角.
1.我们通常在直角坐标系内讨论角,为了方便,使角的顶点与原点重合,角的始边与x轴的非负半轴重合,那么,角的终边在第几象限,就说这个角是第几象限角.
知识梳理
终边落在x轴正半轴上 {α|α=k·360°,k∈Z}
终边落在x轴负半轴上 {α|α=180°+k·360°,k∈Z}
终边落在y轴正半轴上 {α|α=90°+k·360°,k∈Z}
终边落在y轴负半轴上 {α|α=270°+k·360°,k∈Z}
终边落在x轴上 {α|α=k·180°,k∈Z}
终边落在y轴上 {α|α=90°+k·180°,k∈Z}
终边落在坐标轴上 {α|α=k·90°,k∈Z}
2.如果角的终边在坐标轴上,那么就认为这个角不属于任何一个象限.
(1)锐角是第一象限角,钝角是第二象限角,直角的终边在坐标轴上,它不属于任何一个象限;
(2)每一个象限都有正角和负角,无法比较哪一个象限角的大小.
注意点:
(多选)下列结论正确的有
A.-75°是第一象限角 B.225°是第三象限角
C.475°是第二象限角 D.-315°是第四象限角
√
例2
√
因为-90°<-75°<0°,所以-75°是第四象限角;因为180°<225°<270°,所以225°是第三象限角;因为360°+90°<475°<360°+180°,所以475°是第二象限角;因为-360°<-315°<-270°,所以-315°是第一象限角.所以B,C正确.
正确理解象限角与锐角、直角、钝角、平角、周角等概念的关系,需要掌握判断结论正确与否的技巧,判断结论正确需要证明,而判断结论不正确只需举一个反例即可.
反思感悟
(多选)下列叙述不正确的是
A.三角形的内角是第一象限角或第二象限角
B.钝角是第二象限角
C.第二象限角比第一象限角大
D.小于180°的角是钝角、直角或锐角
√
跟踪训练2
√
√
直角不属于任何一个象限,故A不正确;
钝角是大于90°小于180°的角,是第二象限角,故B正确;
由于120°是第二象限角,390°是第一象限角,120°<390°,故C不正确;
由于零角和负角也小于180°,故D不正确.
终边相同的角
三
问题3 给定一个角,它的终边是否唯一?若两角的终边相同,那么这两个角相等吗?
提示 给定一个角,它的终边唯一;两角终边相同,这两个角不一定相等,比如30°角的终边和390°角的终边相同,它们正好相差了360°.
所有与角α终边相同的角,连同角α在内,可构成一个集合S={β|β=α+k·360°,k∈Z},即任一与角α终边相同的角,都可以表示成角α与整数个周角的和.
知识梳理
在与2 110°角终边相同的角中,求满足下列条件的角β.
(1)最大的负角;
例3
与2 110°终边相同的角的集合为{β|β=2 110°+k·360°,k∈Z},
由-360°<2 110°+k·360°<0°,k∈Z,
得-2 470°解得k=-6,故所求的最大负角为β=-50°.
(2)最小的正角;
由0°<2 110°+k·360°<360°,k∈Z,
得-2 110°解得k=-5,故所求的最小正角为β=310°.
(3)在360°~720°范围内的角.
由360°≤2 110°+k·360°≤720°,k∈Z,
得-1 750°≤k·360°≤-1 390°,k∈Z,
解得k=-4,故所求的角为β=670°.
反思感悟
终边相同的角的表示
(1)终边相同的角都可以表示成α+k·360°(k∈Z)的形式.
(2)终边相同的角相差360°的整数倍.
(1)写出终边在直线y= 上的角的集合.
跟踪训练3
因此,终边在直线y= 上的角的集合是S=S1∪S2={α|α=120°+k1·360°,k1∈Z}∪{α|α=300°+k2·360°,k2∈Z},
即S={α|α=120°+2k1·180°,k1∈Z}∪{α|α=120°+(2k2+1)·180°,k2∈Z}={α|α=120°+n·180°,n∈Z}.
故终边在直线y= 上的角的集合是S={α|α=120°+n·180°,n∈Z}.
(2)与-2 024°角终边相同的最小正角是
A.136° B.132°
C.58° D.42°
√
因为-2 024°=-6×360°+136°,所以与-2 024°角终边相同的最小正角是136°.
(3)若角2α与240°角的终边相同,则α等于
A.120°+k·360°,k∈Z
B.120°+k·180°,k∈Z
C.240°+k·360°,k∈Z
D.240°+k·180°,k∈Z
√
角2α与240°角的终边相同,
则2α=240°+k·360°,k∈Z,
则α=120°+k·180°,k∈Z.
区域角的表示
四
问题4 你能否表示出终边落在各个象限的角的集合?
提示 第一象限的角:{α|k·360°<α<90°+k·360°,k∈Z};
第二象限的角:{α|90°+k·360°<α<180°+k·360°,k∈Z};
第三象限的角:{α|180°+k·360°<α<270°+k·360°,k∈Z};
第四象限的角:{α|270°+k·360°<α<360°+k·360°,k∈Z}.
已知角α的终边在图中阴影部分内,试指出角α的取值范围.
例4
终边在30°角的终边所在直线上的角的集合为S1={α|α=30°+k·180°,k∈Z},终边在180°-75°=105°角的终边所在直线上的角的集合为S2={α|α=105°+k·180°,k∈Z},因此,终边在图中阴影部分内的角α的取值范围为{α|30°+k·180°≤α<105°+k·180°,k∈Z}.
延伸探究
1.若将本例题图改为如图所示的图形,那么终边落在阴影部分(包括边界)的角的集合如何表示?
由题干图可知满足题意的角的集合为{β|60°+k·360°≤β≤105°+k·360°,k∈Z}∪{240°+k·360°≤β≤285°+k·360°,k∈Z}={β|60°+2k·180°≤β≤105°+2k·180°,k∈Z}∪{β|60°+(2k+1)·180°≤β≤105°+(2k+1)·180°,k∈Z}={β|60°+n·180°≤
β≤105°+n·180°,n∈Z},即所求的集合为{β|60°+n·180°≤β
≤105°+n·180°,n∈Z}.
2.已知α是第一象限角.
(1)2α是第几象限角?
∵α是第一象限角,∴k·360°<α<90°+k·360°(k∈Z).
∵2k·360°<2α<180°+2k·360°(k∈Z),
∴2α是第一、二象限角或终边在y轴的非负半轴上的角.
方法一 (分类讨论法)因为α是第一象限角,
∴k·360°<α<90°+k·360°,k∈Z,
方法二 (几何法)如图所示,先将各象限分成2等份,再从x轴正半轴的上方起,按逆时针方向依次将各区域标上“一、二、三、四、一、二、三、四”,则标有“一”的区域即为角 的终边所在的区域,故
是第一或第三象限角.
表示区域角的三个步骤
第一步:先按逆时针的方向找到区域的起始和终止边界.
第二步:按由小到大分别标出起始和终止边界对应的-360°~360°范围内的角α和β,写出最简区间{x|α第三步:起始、终止边界对应角α,β再加上360°的整数倍,即得区域角集合.
反思感悟
如图,α,β分别是终边落在OA,OB位置上的两个角,且α=60°,β=315°.
(1)求终边落在阴影部分(不包括边界)的角γ的集合;
跟踪训练4
因为与角β终边相同的一个角可以表示为-45°,所以阴影部分(不包括边界)所表示的角的集合为{γ|-45°+k·360°<γ<60°+k·360°,k∈Z}.
(2)求终边落在阴影部分(不包括边界),且在0°~360°范围内的角θ的集合.
{θ|0°≤θ<60°或315°<θ<360°}.
课堂
小结
1.知识清单:
(1)正角、负角、零角的概念.
(2)终边相同的角的表示.
(3)象限角、区域角的表示.
2.方法归纳:数形结合、分类讨论.
3.常见误区:锐角与小于90°的角的区别,终边相同角的表示中漏掉k∈Z.
随堂演练
1.已知集合A={第二象限角},B={钝角},C={小于180°的角},则A,B,C关系正确的是
A.B=A∩C B.A?C
C.B∪C=C D.A=B=C
√
1
2
3
4
由题意得B?A∩C,故A错误;
A与C互不包含,故B错误;
由B={钝角}?{小于180°的角},所以B∪C=C,故C正确;
由以上分析可知D错误.
2.若α=45°+k·180°,k∈Z,则α的终边在
A.第一、三象限 B.第一、二象限
C.第二、四象限 D.第三、四象限
√
1
2
3
4
因为α=45°+k·180°,k∈Z,所以
当k=2n+1,n∈Z时,α=45°+2n·180°+180°=225°+n·360°,n∈Z,其终边在第三象限;
当k=2n,n∈Z时,α=45°+2n·180°=45°+n·360°,n∈Z,其终边在第一象限.
综上,α的终边在第一、三象限.
3.亲爱的考生,我们数学考试完整的时间是2小时,则从考试开始到结束,钟表的分针转过的角度为 .
1
2
3
4
因为钟表的分针转了两圈,且是按顺时针方向旋转,所以钟表的分针转过的角度为-720°.
-720°
1
2
3
4
4.如图所示.终边落在阴影部分(包括边界)的角α的集合为 .
终边落在OA位置上的角的集合为{α|α=210°+k·360°,k∈Z},终边落在OB位置上的角的集合为{α|α=300°+k·360°,k∈Z}.
故终边落在阴影部分(包括边界)的角的集合是{α|210°+k·360°≤α≤
300°+k·360°,k∈Z}.
{α|210°+k·360°≤α≤300°+k·360°,k∈Z}
本课结束
5.1.1 任意角
第五章 §5.1 任意角和弧度制
1.了解任意角的概念,区分正角、负角与零角.
2.了解象限角的概念,理解并掌握终边相同的角的概念,能写出终边相同的角
所组成的集合.(重点)
3.利用象限角和终边相同的角的概念解决简单的问题.(难点)
学习目标
导语
2022年2月8日,北京冬奥会自由式滑雪女子大跳台决赛展开争夺,谷爱凌在前两轮成绩落后的情况下,第三轮超越自己做出
了此前从未做出过的向左偏轴转体1 620,得到94.50分的高分,也凭借总成绩188.25分夺得了这枚宝贵的金牌!我们该怎样理解向左偏轴转体1 620呢?这和角度是分不开的,为了研究这个问题,我们开始今天的新课.
一、任意角
二、象限角
三、终边相同的角
随堂演练
四、区域角的表示
内容索引
任意角
一
问题1 在初中是如何定义角的?角的范围是多少?
提示 角可以看成一条射线绕着它的端点旋转所成的图形,角的范围是0°~360°.
1.角的概念及其表示
角可以看成一条 绕着它的端点 所成的 .如图,
(1)始边:射线的 位置OA;
终边:射线的 位置OB;
顶点:射线的端点O.
(2)记法:图中的角α可记为“角α”或“∠α”或“∠AOB”.
知识梳理
射线
旋转
图形
起始
终止
名称 定义 图示
正角 一条射线绕其端点按 方向旋转形成的角
负角 一条射线绕其端点按 方向旋转形成的角
零角 一条射线 做任何旋转形成的角
2.任意角:我们把角的概念推广到了任意角,包括正角、负角和零角.
逆时针
顺时针
没有
3.角的相等
如果角α和角β的旋转方向相同且旋转量相等,那么就称 .
4.角的加法
设α,β是任意两个角,把角α的终边旋转角β,这时终边所对应的角是
.
5.相反角:把射线OA绕端点O按不同方向旋转相同的量所成的两个角
叫做互为 ,角α的相反角记为 ,α-β=α+ .
α=β
α+β
相反角
-α
(-β)
如图,射线OA先绕端点O逆时针方向旋转60°到OB处,再按顺时针方向旋转820°至OC处,则β= .
例1
-40°
∠AOC=60°+(-820°)=-760°,
β=-760°+720°=-40°.
弄清角的始边与终边及旋转方向与大小.逆时针旋转形成一个正角,顺时针旋转形成一个负角.正角与负角是表示具有相反意义的旋转量,它的正负规定纯属习惯,就好像正数和负数的规定一样.
反思感悟
图中从OA旋转到OB,OB1,OB2时所成的角度α,β,γ分别是 , , .
跟踪训练1
390°
-150°
60°
题图①中的角是正角,α=390°.
图②中的角,一个是负角、一个是正角,β=-150°,γ=60°.
象限角
二
问题2 初中所学的0°~360°角可以怎样分类?
提示 锐角、直角、钝角、平角和周角.
1.我们通常在直角坐标系内讨论角,为了方便,使角的顶点与原点重合,角的始边与x轴的非负半轴重合,那么,角的终边在第几象限,就说这个角是第几象限角.
知识梳理
终边落在x轴正半轴上 {α|α=k·360°,k∈Z}
终边落在x轴负半轴上 {α|α=180°+k·360°,k∈Z}
终边落在y轴正半轴上 {α|α=90°+k·360°,k∈Z}
终边落在y轴负半轴上 {α|α=270°+k·360°,k∈Z}
终边落在x轴上 {α|α=k·180°,k∈Z}
终边落在y轴上 {α|α=90°+k·180°,k∈Z}
终边落在坐标轴上 {α|α=k·90°,k∈Z}
2.如果角的终边在坐标轴上,那么就认为这个角不属于任何一个象限.
(1)锐角是第一象限角,钝角是第二象限角,直角的终边在坐标轴上,它不属于任何一个象限;
(2)每一个象限都有正角和负角,无法比较哪一个象限角的大小.
注意点:
(多选)下列结论正确的有
A.-75°是第一象限角 B.225°是第三象限角
C.475°是第二象限角 D.-315°是第四象限角
√
例2
√
因为-90°<-75°<0°,所以-75°是第四象限角;因为180°<225°<270°,所以225°是第三象限角;因为360°+90°<475°<360°+180°,所以475°是第二象限角;因为-360°<-315°<-270°,所以-315°是第一象限角.所以B,C正确.
正确理解象限角与锐角、直角、钝角、平角、周角等概念的关系,需要掌握判断结论正确与否的技巧,判断结论正确需要证明,而判断结论不正确只需举一个反例即可.
反思感悟
(多选)下列叙述不正确的是
A.三角形的内角是第一象限角或第二象限角
B.钝角是第二象限角
C.第二象限角比第一象限角大
D.小于180°的角是钝角、直角或锐角
√
跟踪训练2
√
√
直角不属于任何一个象限,故A不正确;
钝角是大于90°小于180°的角,是第二象限角,故B正确;
由于120°是第二象限角,390°是第一象限角,120°<390°,故C不正确;
由于零角和负角也小于180°,故D不正确.
终边相同的角
三
问题3 给定一个角,它的终边是否唯一?若两角的终边相同,那么这两个角相等吗?
提示 给定一个角,它的终边唯一;两角终边相同,这两个角不一定相等,比如30°角的终边和390°角的终边相同,它们正好相差了360°.
所有与角α终边相同的角,连同角α在内,可构成一个集合S={β|β=α+k·360°,k∈Z},即任一与角α终边相同的角,都可以表示成角α与整数个周角的和.
知识梳理
在与2 110°角终边相同的角中,求满足下列条件的角β.
(1)最大的负角;
例3
与2 110°终边相同的角的集合为{β|β=2 110°+k·360°,k∈Z},
由-360°<2 110°+k·360°<0°,k∈Z,
得-2 470°
(2)最小的正角;
由0°<2 110°+k·360°<360°,k∈Z,
得-2 110°
(3)在360°~720°范围内的角.
由360°≤2 110°+k·360°≤720°,k∈Z,
得-1 750°≤k·360°≤-1 390°,k∈Z,
解得k=-4,故所求的角为β=670°.
反思感悟
终边相同的角的表示
(1)终边相同的角都可以表示成α+k·360°(k∈Z)的形式.
(2)终边相同的角相差360°的整数倍.
(1)写出终边在直线y= 上的角的集合.
跟踪训练3
因此,终边在直线y= 上的角的集合是S=S1∪S2={α|α=120°+k1·360°,k1∈Z}∪{α|α=300°+k2·360°,k2∈Z},
即S={α|α=120°+2k1·180°,k1∈Z}∪{α|α=120°+(2k2+1)·180°,k2∈Z}={α|α=120°+n·180°,n∈Z}.
故终边在直线y= 上的角的集合是S={α|α=120°+n·180°,n∈Z}.
(2)与-2 024°角终边相同的最小正角是
A.136° B.132°
C.58° D.42°
√
因为-2 024°=-6×360°+136°,所以与-2 024°角终边相同的最小正角是136°.
(3)若角2α与240°角的终边相同,则α等于
A.120°+k·360°,k∈Z
B.120°+k·180°,k∈Z
C.240°+k·360°,k∈Z
D.240°+k·180°,k∈Z
√
角2α与240°角的终边相同,
则2α=240°+k·360°,k∈Z,
则α=120°+k·180°,k∈Z.
区域角的表示
四
问题4 你能否表示出终边落在各个象限的角的集合?
提示 第一象限的角:{α|k·360°<α<90°+k·360°,k∈Z};
第二象限的角:{α|90°+k·360°<α<180°+k·360°,k∈Z};
第三象限的角:{α|180°+k·360°<α<270°+k·360°,k∈Z};
第四象限的角:{α|270°+k·360°<α<360°+k·360°,k∈Z}.
已知角α的终边在图中阴影部分内,试指出角α的取值范围.
例4
终边在30°角的终边所在直线上的角的集合为S1={α|α=30°+k·180°,k∈Z},终边在180°-75°=105°角的终边所在直线上的角的集合为S2={α|α=105°+k·180°,k∈Z},因此,终边在图中阴影部分内的角α的取值范围为{α|30°+k·180°≤α<105°+k·180°,k∈Z}.
延伸探究
1.若将本例题图改为如图所示的图形,那么终边落在阴影部分(包括边界)的角的集合如何表示?
由题干图可知满足题意的角的集合为{β|60°+k·360°≤β≤105°+k·360°,k∈Z}∪{240°+k·360°≤β≤285°+k·360°,k∈Z}={β|60°+2k·180°≤β≤105°+2k·180°,k∈Z}∪{β|60°+(2k+1)·180°≤β≤105°+(2k+1)·180°,k∈Z}={β|60°+n·180°≤
β≤105°+n·180°,n∈Z},即所求的集合为{β|60°+n·180°≤β
≤105°+n·180°,n∈Z}.
2.已知α是第一象限角.
(1)2α是第几象限角?
∵α是第一象限角,∴k·360°<α<90°+k·360°(k∈Z).
∵2k·360°<2α<180°+2k·360°(k∈Z),
∴2α是第一、二象限角或终边在y轴的非负半轴上的角.
方法一 (分类讨论法)因为α是第一象限角,
∴k·360°<α<90°+k·360°,k∈Z,
方法二 (几何法)如图所示,先将各象限分成2等份,再从x轴正半轴的上方起,按逆时针方向依次将各区域标上“一、二、三、四、一、二、三、四”,则标有“一”的区域即为角 的终边所在的区域,故
是第一或第三象限角.
表示区域角的三个步骤
第一步:先按逆时针的方向找到区域的起始和终止边界.
第二步:按由小到大分别标出起始和终止边界对应的-360°~360°范围内的角α和β,写出最简区间{x|α
反思感悟
如图,α,β分别是终边落在OA,OB位置上的两个角,且α=60°,β=315°.
(1)求终边落在阴影部分(不包括边界)的角γ的集合;
跟踪训练4
因为与角β终边相同的一个角可以表示为-45°,所以阴影部分(不包括边界)所表示的角的集合为{γ|-45°+k·360°<γ<60°+k·360°,k∈Z}.
(2)求终边落在阴影部分(不包括边界),且在0°~360°范围内的角θ的集合.
{θ|0°≤θ<60°或315°<θ<360°}.
课堂
小结
1.知识清单:
(1)正角、负角、零角的概念.
(2)终边相同的角的表示.
(3)象限角、区域角的表示.
2.方法归纳:数形结合、分类讨论.
3.常见误区:锐角与小于90°的角的区别,终边相同角的表示中漏掉k∈Z.
随堂演练
1.已知集合A={第二象限角},B={钝角},C={小于180°的角},则A,B,C关系正确的是
A.B=A∩C B.A?C
C.B∪C=C D.A=B=C
√
1
2
3
4
由题意得B?A∩C,故A错误;
A与C互不包含,故B错误;
由B={钝角}?{小于180°的角},所以B∪C=C,故C正确;
由以上分析可知D错误.
2.若α=45°+k·180°,k∈Z,则α的终边在
A.第一、三象限 B.第一、二象限
C.第二、四象限 D.第三、四象限
√
1
2
3
4
因为α=45°+k·180°,k∈Z,所以
当k=2n+1,n∈Z时,α=45°+2n·180°+180°=225°+n·360°,n∈Z,其终边在第三象限;
当k=2n,n∈Z时,α=45°+2n·180°=45°+n·360°,n∈Z,其终边在第一象限.
综上,α的终边在第一、三象限.
3.亲爱的考生,我们数学考试完整的时间是2小时,则从考试开始到结束,钟表的分针转过的角度为 .
1
2
3
4
因为钟表的分针转了两圈,且是按顺时针方向旋转,所以钟表的分针转过的角度为-720°.
-720°
1
2
3
4
4.如图所示.终边落在阴影部分(包括边界)的角α的集合为 .
终边落在OA位置上的角的集合为{α|α=210°+k·360°,k∈Z},终边落在OB位置上的角的集合为{α|α=300°+k·360°,k∈Z}.
故终边落在阴影部分(包括边界)的角的集合是{α|210°+k·360°≤α≤
300°+k·360°,k∈Z}.
{α|210°+k·360°≤α≤300°+k·360°,k∈Z}
本课结束
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
