第五章 §5.1 5.1.2 弧度制-高中数学人教A版必修一 课件(共48张PPT)
文档属性
| 名称 | 第五章 §5.1 5.1.2 弧度制-高中数学人教A版必修一 课件(共48张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-27 00:00:00 | ||
图片预览











文档简介
(共44张PPT)
5.1.2 弧度制
第五章 §5.1 任意角和弧度制
1.了解弧度制的概念,能进行弧度与角度的相互转化.(重点)
2.掌握弧度制下的扇形的弧长和面积公式.(难点)
学习目标
导语
同学们,大家看过《水浒传》吗?在古典小说中,经常看到“某人身高八尺”这样的说法,若按照我们今天的标准(1米=3尺)换算,这些人的身高都超过了姚明的身高,难道古人真的都有那么高吗?其实不然,在我国历史的不同时期,一尺的标准是不一样的,比如在春秋战国时期,一尺约等于0.23米,这样算来,八尺也就1.84米,“堂堂七尺男儿”也就1.6米左右.据说在商代的时候,一尺约等于0.17米,人高约一丈(一丈等于十尺),故有“丈夫”之称,那么度量角的大小,除了角度以外,还有其他单位吗?让我们带着这个疑问开始今天的新课.
一、弧度制的概念
二、角度制与弧度制的相互转化
三、利用弧度表示角
随堂演练
四、弧度制下的扇形的弧长与面积公式
内容索引
弧度制的概念
一
问题1 我们上节课所学习的角度制能否与实数建立一一对应的关系?
提示 不能,比如30°2′11′′,这种表示不能与实数建立一一对应的关系.
问题2 为了能把角和实数建立联系,经过几千年的发展、探究和讨论,人们在衡量角度上达成共识,形成了今天的弧度制.提到弧度,你能想到什么?
提示 我们能够想到足球射门的弧度、篮球投篮的弧度,我们认知的弧度是非常简单的形状,也正是因为有了弧度才完美,比如:海浪因弧度而活跃;嘴角因为有弧度而美丽;月有阴晴圆缺,正是因为有弧度而富有神韵.而在我们数学中,正是因为弧度的引入,给数学学科带来了巨大的改变.
角度制 定义 用度作为单位来度量角的单位制
1度的角
1度的角等于周角的 ,记作1°
弧度制 定义 以弧度作为单位来度量角的单位制
1弧度的角 长度等于 的圆弧所对的圆心角叫做1弧度的角.1弧度记作1 rad(rad可省略不写)
1.度量角的两种制度
知识梳理
半径长
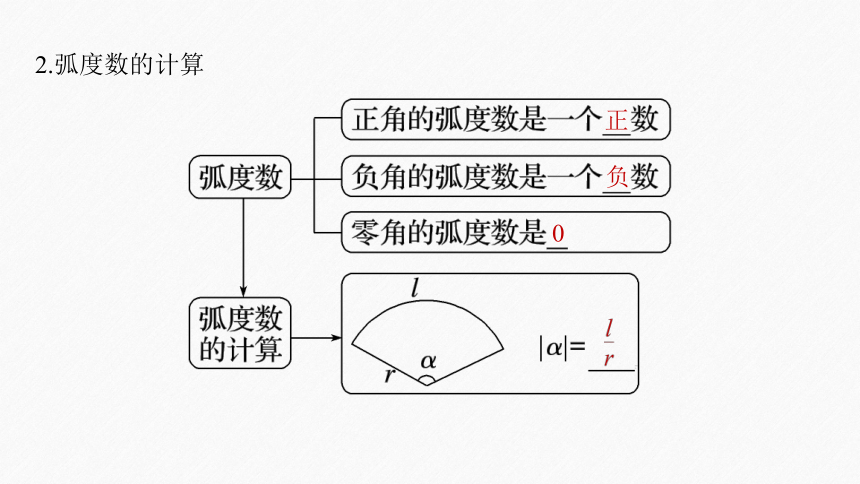
2.弧度数的计算
正
负
0
一定大小的圆心角α所对应的弧长和半径的比值是唯一确定的,与半径大小无关.
注意点:
下列命题中,假命题是
A.“度”与“弧度”是度量角的两种不同的度量单位
B.1°的角是周角的 ,1 rad的角是周角的
C.1 rad的角比1°的角要大
D.用角度制和弧度制度量角,都与圆的半径有关
√
例1
根据1度的角、1弧度的角的定义可知D为假命题.
(1)圆心角α所对应的弧长和半径的比值是唯一确定的;
(2)任意角的弧度数与实数是一一对应的关系.
反思感悟
下列各命题中,真命题是
A.1弧度就是1°的圆心角所对的弧
B.1弧度是长度等于半径的弧
C.1弧度是1°的弧与1°的角之和
D.1弧度是长度等于半径长的弧所对的圆心角的大小
√
跟踪训练1
根据弧度制和角度制的规定可知A,B,C均错误,D正确.
角度制与弧度制的相互转化
二
问题3 根据公式|α|= ,你能得出圆周角的弧度数吗?
提示 因为半径为r的圆的周长为l=2πr,故圆周角的弧度数α=2π,而圆周角的角度数是360°,于是我们有了弧度与角度的换算关系.
1.弧度与角度的换算
知识梳理
2.一些特殊角的度数与弧度数的对应关系
度 0° 30° 45° _____ 90° 120°
弧度 ___
度 135° 150° ______ 270° 360°
弧度 π 2π
60°
180°
0
(1)弧度单位rad可以省略;
(2)在同一个题目中,弧度与角度不能混用.
注意点:
把下列角度化成弧度,弧度化成角度:
(1)37°30′;
例2
(2)-216°;
(3)2;
角度与弧度换算技巧
在进行角度与弧度的换算时,抓住关系式π rad=180°是关键,由它可以得到:度数× =弧度数,弧度数× =度数.一般情况下,省略弧度单位rad.
反思感悟
将下列角度与弧度进行互化:
跟踪训练2
(3)10°;
(4)-855°.
利用弧度表示角
三
将-1 125°角写成α+2kπ(k∈Z)的形式,其中0≤α<2π,并判断它是第几象限角?
例3
所以-1 125°角是第四象限角.
延伸探究 若在本例的条件下,在[-4π,4π]范围内找出与α终边相同的角的集合.
得k=-2,-1,0,1,
反思感悟
用弧度制表示终边相同的角的两个关注点
(1)用弧度制表示终边相同的角α+2kπ(k∈Z)时,其中2kπ是π的偶数倍,而不是整数倍.
(2)注意同一题目中角度制与弧度制不能混用.
(1)用弧度制表示所有与75°角终边相同的角的集合是
.
跟踪训练3
√
(2)将手表的分针拨快10分钟,则分针在旋转过程中形成的角的弧度数是
弧度制下的扇形的弧长与面积公式
四
问题4 我们初中所学扇形的弧长和面积公式是什么?
公式 度量制 弧长公式 扇形面积公式
角度制
弧度制 l= (0<α<2π)
S= =______
(0<α<2π)
扇形的弧长与面积公式(R是扇形所在圆的半径,n°为扇形的圆心角)
知识梳理
αR
已知扇形的周长为10 cm,面积为4 cm2,求扇形圆心角的弧度数.
例4
设扇形圆心角的弧度数为θ(0<θ<2π),弧长为l cm,半径为R cm,
①
②
整理得R2-5R+4=0,解得R=1或R=4.
当R=1时,l=8,此时,θ=8 rad>2π rad,舍去.
延伸探究 已知一扇形的周长为4,当它的半径与圆心角取何值时,扇形的面积最大?最大值是多少?
设扇形圆心角的弧度数为θ(0<θ<2π),弧长为l,半径为r,面积为S,
所以当r=1时,S最大,且Smax=1,
所以当圆心角为2时扇形面积最大,最大值为1.
扇形的弧长和面积的求解策略
反思感悟
(2)找关键:涉及扇形的半径、周长、弧长、圆心角、面积等的计算问题,关键是分析题目中已知哪些量、要求哪些量,然后灵活运用弧长公式、扇形的面积公式直接求解或列方程(组)求解.
已知扇形的圆心角是α,半径为r,弧长为l.
(1)若α=135°,r=10,求扇形的弧长l;
跟踪训练4
(2)若扇形AOB的周长为22,当扇形的圆心角α为多少弧度时,这个扇形的面积最大,并求出此时扇形的面积S的最大值.
课堂
小结
1.知识清单:
(1)弧度制的概念.
(2)弧度与角度的相互转化.
(3)掌握特殊角的度数与弧度数的对应关系.
(4)扇形的弧长与面积的计算.
2.方法归纳:由特殊到一般、数学运算.
3.常见误区:弧度与角度易混用.
随堂演练
1.下列说法正确的是
A.1弧度的圆心角所对的弧长等于半径
B.大圆中1弧度的圆心角比小圆中1弧度的圆心角大
C.所有圆心角为1弧度的角所对的弧长都相等
D.用弧度表示的角都是正角
√
1
2
3
4
对于A,根据弧度的定义知,“1弧度的圆心角所对的弧长等于半径”,故A正确;
对于B,大圆中1弧度的圆心角与小圆中1弧度的圆心角相等,故B错误;
对于C,只有在同圆或等圆中,1弧度的圆心角所对的弧长是相等的,故C错误;
对于D,用弧度表示的角也可以是负角或零角,故D错误.
1
2
3
4
2.-660°等于
√
1
2
3
4
3.时钟的分针在1点到3点20分这段时间里转过的弧度为
√
1
2
3
4
1
2
3
4
4.已知一个扇形的弧长等于其所在圆半径的2倍,则该扇形圆心角的弧度数为 ,若该扇形的半径为1,则该扇形的面积为 .
2
1
本课结束
5.1.2 弧度制
第五章 §5.1 任意角和弧度制
1.了解弧度制的概念,能进行弧度与角度的相互转化.(重点)
2.掌握弧度制下的扇形的弧长和面积公式.(难点)
学习目标
导语
同学们,大家看过《水浒传》吗?在古典小说中,经常看到“某人身高八尺”这样的说法,若按照我们今天的标准(1米=3尺)换算,这些人的身高都超过了姚明的身高,难道古人真的都有那么高吗?其实不然,在我国历史的不同时期,一尺的标准是不一样的,比如在春秋战国时期,一尺约等于0.23米,这样算来,八尺也就1.84米,“堂堂七尺男儿”也就1.6米左右.据说在商代的时候,一尺约等于0.17米,人高约一丈(一丈等于十尺),故有“丈夫”之称,那么度量角的大小,除了角度以外,还有其他单位吗?让我们带着这个疑问开始今天的新课.
一、弧度制的概念
二、角度制与弧度制的相互转化
三、利用弧度表示角
随堂演练
四、弧度制下的扇形的弧长与面积公式
内容索引
弧度制的概念
一
问题1 我们上节课所学习的角度制能否与实数建立一一对应的关系?
提示 不能,比如30°2′11′′,这种表示不能与实数建立一一对应的关系.
问题2 为了能把角和实数建立联系,经过几千年的发展、探究和讨论,人们在衡量角度上达成共识,形成了今天的弧度制.提到弧度,你能想到什么?
提示 我们能够想到足球射门的弧度、篮球投篮的弧度,我们认知的弧度是非常简单的形状,也正是因为有了弧度才完美,比如:海浪因弧度而活跃;嘴角因为有弧度而美丽;月有阴晴圆缺,正是因为有弧度而富有神韵.而在我们数学中,正是因为弧度的引入,给数学学科带来了巨大的改变.
角度制 定义 用度作为单位来度量角的单位制
1度的角
1度的角等于周角的 ,记作1°
弧度制 定义 以弧度作为单位来度量角的单位制
1弧度的角 长度等于 的圆弧所对的圆心角叫做1弧度的角.1弧度记作1 rad(rad可省略不写)
1.度量角的两种制度
知识梳理
半径长
2.弧度数的计算
正
负
0
一定大小的圆心角α所对应的弧长和半径的比值是唯一确定的,与半径大小无关.
注意点:
下列命题中,假命题是
A.“度”与“弧度”是度量角的两种不同的度量单位
B.1°的角是周角的 ,1 rad的角是周角的
C.1 rad的角比1°的角要大
D.用角度制和弧度制度量角,都与圆的半径有关
√
例1
根据1度的角、1弧度的角的定义可知D为假命题.
(1)圆心角α所对应的弧长和半径的比值是唯一确定的;
(2)任意角的弧度数与实数是一一对应的关系.
反思感悟
下列各命题中,真命题是
A.1弧度就是1°的圆心角所对的弧
B.1弧度是长度等于半径的弧
C.1弧度是1°的弧与1°的角之和
D.1弧度是长度等于半径长的弧所对的圆心角的大小
√
跟踪训练1
根据弧度制和角度制的规定可知A,B,C均错误,D正确.
角度制与弧度制的相互转化
二
问题3 根据公式|α|= ,你能得出圆周角的弧度数吗?
提示 因为半径为r的圆的周长为l=2πr,故圆周角的弧度数α=2π,而圆周角的角度数是360°,于是我们有了弧度与角度的换算关系.
1.弧度与角度的换算
知识梳理
2.一些特殊角的度数与弧度数的对应关系
度 0° 30° 45° _____ 90° 120°
弧度 ___
度 135° 150° ______ 270° 360°
弧度 π 2π
60°
180°
0
(1)弧度单位rad可以省略;
(2)在同一个题目中,弧度与角度不能混用.
注意点:
把下列角度化成弧度,弧度化成角度:
(1)37°30′;
例2
(2)-216°;
(3)2;
角度与弧度换算技巧
在进行角度与弧度的换算时,抓住关系式π rad=180°是关键,由它可以得到:度数× =弧度数,弧度数× =度数.一般情况下,省略弧度单位rad.
反思感悟
将下列角度与弧度进行互化:
跟踪训练2
(3)10°;
(4)-855°.
利用弧度表示角
三
将-1 125°角写成α+2kπ(k∈Z)的形式,其中0≤α<2π,并判断它是第几象限角?
例3
所以-1 125°角是第四象限角.
延伸探究 若在本例的条件下,在[-4π,4π]范围内找出与α终边相同的角的集合.
得k=-2,-1,0,1,
反思感悟
用弧度制表示终边相同的角的两个关注点
(1)用弧度制表示终边相同的角α+2kπ(k∈Z)时,其中2kπ是π的偶数倍,而不是整数倍.
(2)注意同一题目中角度制与弧度制不能混用.
(1)用弧度制表示所有与75°角终边相同的角的集合是
.
跟踪训练3
√
(2)将手表的分针拨快10分钟,则分针在旋转过程中形成的角的弧度数是
弧度制下的扇形的弧长与面积公式
四
问题4 我们初中所学扇形的弧长和面积公式是什么?
公式 度量制 弧长公式 扇形面积公式
角度制
弧度制 l= (0<α<2π)
S= =______
(0<α<2π)
扇形的弧长与面积公式(R是扇形所在圆的半径,n°为扇形的圆心角)
知识梳理
αR
已知扇形的周长为10 cm,面积为4 cm2,求扇形圆心角的弧度数.
例4
设扇形圆心角的弧度数为θ(0<θ<2π),弧长为l cm,半径为R cm,
①
②
整理得R2-5R+4=0,解得R=1或R=4.
当R=1时,l=8,此时,θ=8 rad>2π rad,舍去.
延伸探究 已知一扇形的周长为4,当它的半径与圆心角取何值时,扇形的面积最大?最大值是多少?
设扇形圆心角的弧度数为θ(0<θ<2π),弧长为l,半径为r,面积为S,
所以当r=1时,S最大,且Smax=1,
所以当圆心角为2时扇形面积最大,最大值为1.
扇形的弧长和面积的求解策略
反思感悟
(2)找关键:涉及扇形的半径、周长、弧长、圆心角、面积等的计算问题,关键是分析题目中已知哪些量、要求哪些量,然后灵活运用弧长公式、扇形的面积公式直接求解或列方程(组)求解.
已知扇形的圆心角是α,半径为r,弧长为l.
(1)若α=135°,r=10,求扇形的弧长l;
跟踪训练4
(2)若扇形AOB的周长为22,当扇形的圆心角α为多少弧度时,这个扇形的面积最大,并求出此时扇形的面积S的最大值.
课堂
小结
1.知识清单:
(1)弧度制的概念.
(2)弧度与角度的相互转化.
(3)掌握特殊角的度数与弧度数的对应关系.
(4)扇形的弧长与面积的计算.
2.方法归纳:由特殊到一般、数学运算.
3.常见误区:弧度与角度易混用.
随堂演练
1.下列说法正确的是
A.1弧度的圆心角所对的弧长等于半径
B.大圆中1弧度的圆心角比小圆中1弧度的圆心角大
C.所有圆心角为1弧度的角所对的弧长都相等
D.用弧度表示的角都是正角
√
1
2
3
4
对于A,根据弧度的定义知,“1弧度的圆心角所对的弧长等于半径”,故A正确;
对于B,大圆中1弧度的圆心角与小圆中1弧度的圆心角相等,故B错误;
对于C,只有在同圆或等圆中,1弧度的圆心角所对的弧长是相等的,故C错误;
对于D,用弧度表示的角也可以是负角或零角,故D错误.
1
2
3
4
2.-660°等于
√
1
2
3
4
3.时钟的分针在1点到3点20分这段时间里转过的弧度为
√
1
2
3
4
1
2
3
4
4.已知一个扇形的弧长等于其所在圆半径的2倍,则该扇形圆心角的弧度数为 ,若该扇形的半径为1,则该扇形的面积为 .
2
1
本课结束
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
