第五章 §5.3 第2课时诱导公式(二)-高中数学人教A版必修一 课件(共31张PPT)
文档属性
| 名称 | 第五章 §5.3 第2课时诱导公式(二)-高中数学人教A版必修一 课件(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-27 06:18:06 | ||
图片预览











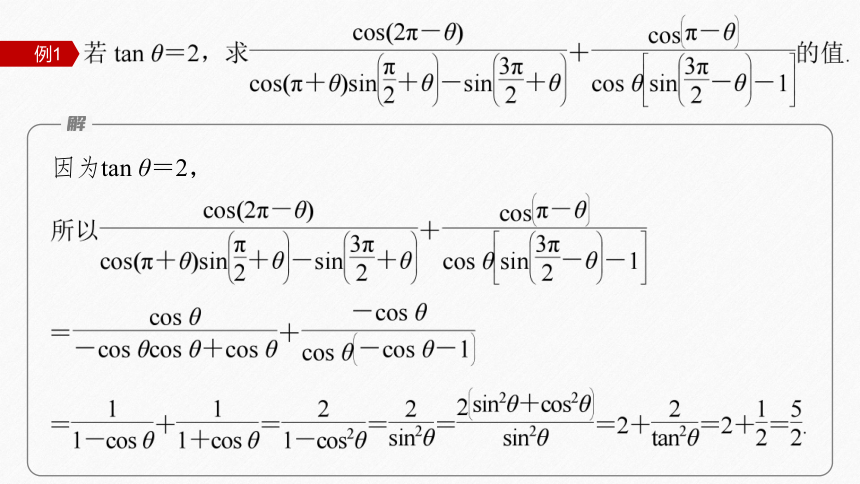
文档简介
(共31张PPT)
第2课时 诱导公式(二)
第五章 §5.3 诱导公式
1.理解公式五、六的推导过程并识记诱导公式,理解和掌握公式的内涵及结构
特征.(重点)
2.会初步运用诱导公式求三角函数的值,并进行简单三角函数式的化简.(难点)
学习目标
导语
回顾前面的学习,我们利用单位圆定义了三角函数,利用单位圆推出了一组神奇的公式,利用它可以把任意角的三角函数转化为锐角三角函数.单位圆是一个多么美妙的图形,它就像一轮光芒四射的太阳,照耀我们的探究之路,又像一艘轮船,引领我们在知识的海洋里航行,这节课,让我们继续在单位圆中探寻三角函数的奥秘吧!
一、公式五、六
二、化简求值
三、诱导公式的综合应用
随堂演练
内容索引
公式五、六
一
问题1 回顾上节课我们推导公式二的过程.
提示 利用了单位圆的对称性,作了点P1关于原点对称的点.
提示 如图,过点P1向x轴作垂线,垂足为A,过点P5向y轴作垂线,垂足为B,由图象的对称性可知,∠AOP1=∠BOP5=α,故OP5为 -α的终边,以OP5为
终边的角γ可以表示为γ=2kπ+ (k∈Z),在Rt△AOP1和Rt△BOP5中,OP1=OP5,故△AOP1≌△BOP5,即
问题2 观察右图,我们作了点P1关于直线y=x的对称点P5,你能发现这两点有什么关系吗?
P1的横坐标与P5的纵坐标相同,P1的纵坐标与P5的横坐标相同,若点P1的坐标为(x,y),则点P5的坐标为(y,x)(同学们还记得我们当初学习对数
函数时,提到过反函数是关于y=x对称的,定义域和值域相反,是不是和此处有相似之处),现在我们知道了两角的终边与单位圆的交点坐标,根据三角函数的定义,于是我们可以得到sin α=y,cos α=x;cos
=y,sin =x.大家自己动手,如果我们作P5关于y轴的对称点P6,此时它和P1,P5这两点有什么关系?
知识梳理
cos α
-sin α
(1)名称发生了变化,实现了正弦和余弦的相互转化;
(2)运用公式时,把α看成锐角;
(3)符号的变化要看把α看成锐角时所在的象限.
注意点:
化简求值
二
例1
因为tan θ=2,
利用诱导公式化简、求值的策略
(1)已知角求值问题,关键是利用诱导公式把任意的三角函数值转化成锐角的三角函数值求解,转化过程中注意口诀“奇变偶不变,符号看象限”的应用.
(2)对式子进行化简或求值时,要注意要求的角与已知角之间的关系,并结合诱导公式进行转化,特别要注意角的范围.
反思感悟
反思感悟
跟踪训练1
诱导公式的综合应用
三
(1)已知cos 31°=m,则sin 239°tan 149°的值是
√
例2
sin 239°tan 149°
=sin(180°+59°)tan(180°-31°)
=-sin 59°(-tan 31°)
=-sin(90°-31°)(-tan 31°)
=-cos 31°(-tan 31°)=sin 31°
√
延伸探究
因为α是第三象限角,所以-α是第二象限角,
反思感悟
诱导公式综合应用要“三看”
一看角:①化大为小;②看角与角间的联系,可通过相加、相减分析两角的关系.
二看函数名称:一般是弦切互化.
三看式子结构:通过分析式子,选择合适的方法,如分式可对分子分母同乘一个式子变形,平方和差、立方和差公式.
跟踪训练2
课堂
小结
1.知识清单:
(1)公式五、六.
(2)利用诱导公式进行化简、求值与证明.
2.方法归纳:公式法、角的构造.
3.常见误区:函数符号的变化,角与角之间的联系与构造.
随堂演练
√
1
2
3
4
√
1
2
3
4
√
1
2
3
4
1
2
3
4
√
本课结束
第2课时 诱导公式(二)
第五章 §5.3 诱导公式
1.理解公式五、六的推导过程并识记诱导公式,理解和掌握公式的内涵及结构
特征.(重点)
2.会初步运用诱导公式求三角函数的值,并进行简单三角函数式的化简.(难点)
学习目标
导语
回顾前面的学习,我们利用单位圆定义了三角函数,利用单位圆推出了一组神奇的公式,利用它可以把任意角的三角函数转化为锐角三角函数.单位圆是一个多么美妙的图形,它就像一轮光芒四射的太阳,照耀我们的探究之路,又像一艘轮船,引领我们在知识的海洋里航行,这节课,让我们继续在单位圆中探寻三角函数的奥秘吧!
一、公式五、六
二、化简求值
三、诱导公式的综合应用
随堂演练
内容索引
公式五、六
一
问题1 回顾上节课我们推导公式二的过程.
提示 利用了单位圆的对称性,作了点P1关于原点对称的点.
提示 如图,过点P1向x轴作垂线,垂足为A,过点P5向y轴作垂线,垂足为B,由图象的对称性可知,∠AOP1=∠BOP5=α,故OP5为 -α的终边,以OP5为
终边的角γ可以表示为γ=2kπ+ (k∈Z),在Rt△AOP1和Rt△BOP5中,OP1=OP5,故△AOP1≌△BOP5,即
问题2 观察右图,我们作了点P1关于直线y=x的对称点P5,你能发现这两点有什么关系吗?
P1的横坐标与P5的纵坐标相同,P1的纵坐标与P5的横坐标相同,若点P1的坐标为(x,y),则点P5的坐标为(y,x)(同学们还记得我们当初学习对数
函数时,提到过反函数是关于y=x对称的,定义域和值域相反,是不是和此处有相似之处),现在我们知道了两角的终边与单位圆的交点坐标,根据三角函数的定义,于是我们可以得到sin α=y,cos α=x;cos
=y,sin =x.大家自己动手,如果我们作P5关于y轴的对称点P6,此时它和P1,P5这两点有什么关系?
知识梳理
cos α
-sin α
(1)名称发生了变化,实现了正弦和余弦的相互转化;
(2)运用公式时,把α看成锐角;
(3)符号的变化要看把α看成锐角时所在的象限.
注意点:
化简求值
二
例1
因为tan θ=2,
利用诱导公式化简、求值的策略
(1)已知角求值问题,关键是利用诱导公式把任意的三角函数值转化成锐角的三角函数值求解,转化过程中注意口诀“奇变偶不变,符号看象限”的应用.
(2)对式子进行化简或求值时,要注意要求的角与已知角之间的关系,并结合诱导公式进行转化,特别要注意角的范围.
反思感悟
反思感悟
跟踪训练1
诱导公式的综合应用
三
(1)已知cos 31°=m,则sin 239°tan 149°的值是
√
例2
sin 239°tan 149°
=sin(180°+59°)tan(180°-31°)
=-sin 59°(-tan 31°)
=-sin(90°-31°)(-tan 31°)
=-cos 31°(-tan 31°)=sin 31°
√
延伸探究
因为α是第三象限角,所以-α是第二象限角,
反思感悟
诱导公式综合应用要“三看”
一看角:①化大为小;②看角与角间的联系,可通过相加、相减分析两角的关系.
二看函数名称:一般是弦切互化.
三看式子结构:通过分析式子,选择合适的方法,如分式可对分子分母同乘一个式子变形,平方和差、立方和差公式.
跟踪训练2
课堂
小结
1.知识清单:
(1)公式五、六.
(2)利用诱导公式进行化简、求值与证明.
2.方法归纳:公式法、角的构造.
3.常见误区:函数符号的变化,角与角之间的联系与构造.
随堂演练
√
1
2
3
4
√
1
2
3
4
√
1
2
3
4
1
2
3
4
√
本课结束
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
