第五章 §5.3 第3课时 公式的综合应用-高中数学人教A版必修一 课件(共35张PPT)
文档属性
| 名称 | 第五章 §5.3 第3课时 公式的综合应用-高中数学人教A版必修一 课件(共35张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-27 06:18:39 | ||
图片预览







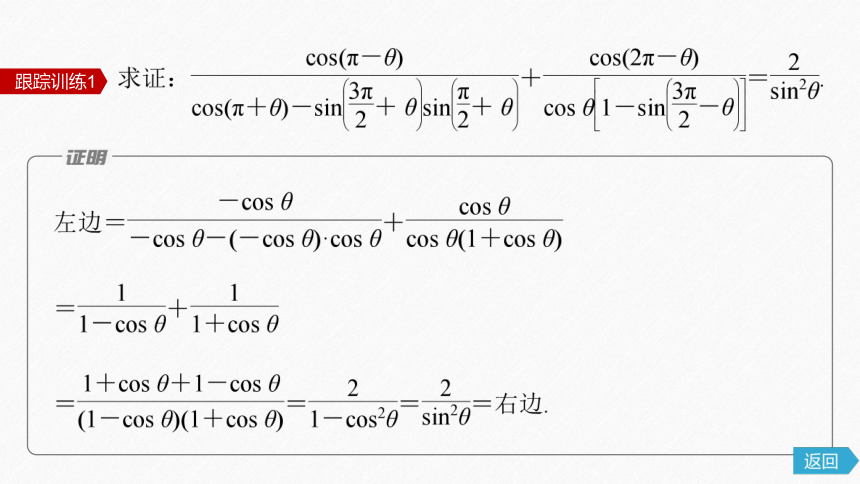




文档简介
(共35张PPT)
第3课时 公式的综合应用
第五章 §5.3 诱导公式
1.熟练掌握六组诱导公式的结构特征.(重点)
2.会利用六组诱导公式求值、证明.(难点)
学习目标
导语
同学们,经过前两节课的学习,我们掌握了三角函数的诱导公式一~六,你掌握记忆的技巧了吗?其实,它们可以统一概括为α+k· (k∈Z)的三角函数值,等于α的同名(k是偶数时)或异名(k是奇数时)三角函数值,前面加上一个将α看成锐角时原函数值的符号,简称为“奇变偶不变,符号看象限”.
一、利用诱导公式证明恒等式
二、诱导公式在实际问题中的应用
三、分类讨论在三角函数中的应用
随堂演练
四、诱导公式的综合应用
内容索引
利用诱导公式证明恒等式
一
例1
∴左边=右边,故原等式成立.
三角恒等式的证明策略
对于三角恒等式的证明,应遵循化繁为简的原则,从左边推到右边或从右边推到左边,也可以用左右归一、变更论证的方法.常用定义法、化弦法、拆项拆角法、“1”的代换法、公式变形法,要熟练掌握基本公式,善于从中选择巧妙简捷的方法.
反思感悟
跟踪训练1
诱导公式在实际问题中的应用
二
问题1 三角形中其中一个角与另外两角和是什么关系?
提示 互补.
问题2 直角三角形中,两锐角是什么关系?
提示 互余.
sin C
知识梳理
-cos C
例2
因为A+B+C=π,
所以A+B-C=π-2C,A-B+C=π-2B.
所以cos C=cos B.
又B,C为△ABC的内角,所以C=B,所以△ABC为等腰三角形.
在涉及三角形问题时,一定要注意根据三角形内角和A+B+C=π以及题目的具体条件进行适当变形,再化简求值.
反思感悟
在△ABC中,下列各表达式为常数的是
√
跟踪训练2
在△ABC中,A+B+C=π,
对于选项A,sin(A+B)+sin C=2sin C,不为常数;
对于选项B,cos(B+C)-cos A=-2cos A,不为常数;
分类讨论在三角函数中的应用
三
例3
①当k=2n+1,n∈Z时,
②当k=2n,n∈Z时,
反思感悟
根据诱导公式,一般要对三角函数中π前的系数是奇数还是偶数进行分类讨论.
√
跟踪训练3
若k为偶数,可设k=2n(n∈Z),
若k为奇数,可设k=2n+1(n∈Z),
诱导公式的综合应用
四
(1)求sin α的值;
例4
因为α为第三象限角,
用诱导公式化简求值的方法
(1)对于三角函数式的化简求值问题,一般遵循诱导公式先行的原则,即先用诱导公式化简变形,达到角的统一,再进行切化弦,以保证三角函数名最少.
(2)对于π±α和 ±α这两组诱导公式,切记运用前一组公式不变名,而运用后一组公式必须变名.
反思感悟
跟踪训练4
√
课堂
小结
1.知识清单:
(1)利用诱导公式证明恒等式.
(2)诱导公式在实际问题中的应用.
(3)分类讨论在三角函数中的应用.
2.方法归纳:公式法、分类讨论法.
3.常见误区:易忽视实际问题中角的范围.
随堂演练
1.在△ABC中,cos(A+B)的值等于
A.cos C B.-cos C
C.sin C D.-sin C
√
1
2
3
4
由于A+B+C=π,
所以A+B=π-C.
所以cos(A+B)=cos(π-C)=-cos C.
2.已知sin 28°=a,则cos(-602°)等于
√
1
2
3
4
cos(-602°)=cos(2×360°-602°)=cos 118°=cos(90°+28°)=-sin 28°=-a.
A.-2 B.-1 C.1 D.2
1
2
3
4
√
1
2
3
4
本课结束
第3课时 公式的综合应用
第五章 §5.3 诱导公式
1.熟练掌握六组诱导公式的结构特征.(重点)
2.会利用六组诱导公式求值、证明.(难点)
学习目标
导语
同学们,经过前两节课的学习,我们掌握了三角函数的诱导公式一~六,你掌握记忆的技巧了吗?其实,它们可以统一概括为α+k· (k∈Z)的三角函数值,等于α的同名(k是偶数时)或异名(k是奇数时)三角函数值,前面加上一个将α看成锐角时原函数值的符号,简称为“奇变偶不变,符号看象限”.
一、利用诱导公式证明恒等式
二、诱导公式在实际问题中的应用
三、分类讨论在三角函数中的应用
随堂演练
四、诱导公式的综合应用
内容索引
利用诱导公式证明恒等式
一
例1
∴左边=右边,故原等式成立.
三角恒等式的证明策略
对于三角恒等式的证明,应遵循化繁为简的原则,从左边推到右边或从右边推到左边,也可以用左右归一、变更论证的方法.常用定义法、化弦法、拆项拆角法、“1”的代换法、公式变形法,要熟练掌握基本公式,善于从中选择巧妙简捷的方法.
反思感悟
跟踪训练1
诱导公式在实际问题中的应用
二
问题1 三角形中其中一个角与另外两角和是什么关系?
提示 互补.
问题2 直角三角形中,两锐角是什么关系?
提示 互余.
sin C
知识梳理
-cos C
例2
因为A+B+C=π,
所以A+B-C=π-2C,A-B+C=π-2B.
所以cos C=cos B.
又B,C为△ABC的内角,所以C=B,所以△ABC为等腰三角形.
在涉及三角形问题时,一定要注意根据三角形内角和A+B+C=π以及题目的具体条件进行适当变形,再化简求值.
反思感悟
在△ABC中,下列各表达式为常数的是
√
跟踪训练2
在△ABC中,A+B+C=π,
对于选项A,sin(A+B)+sin C=2sin C,不为常数;
对于选项B,cos(B+C)-cos A=-2cos A,不为常数;
分类讨论在三角函数中的应用
三
例3
①当k=2n+1,n∈Z时,
②当k=2n,n∈Z时,
反思感悟
根据诱导公式,一般要对三角函数中π前的系数是奇数还是偶数进行分类讨论.
√
跟踪训练3
若k为偶数,可设k=2n(n∈Z),
若k为奇数,可设k=2n+1(n∈Z),
诱导公式的综合应用
四
(1)求sin α的值;
例4
因为α为第三象限角,
用诱导公式化简求值的方法
(1)对于三角函数式的化简求值问题,一般遵循诱导公式先行的原则,即先用诱导公式化简变形,达到角的统一,再进行切化弦,以保证三角函数名最少.
(2)对于π±α和 ±α这两组诱导公式,切记运用前一组公式不变名,而运用后一组公式必须变名.
反思感悟
跟踪训练4
√
课堂
小结
1.知识清单:
(1)利用诱导公式证明恒等式.
(2)诱导公式在实际问题中的应用.
(3)分类讨论在三角函数中的应用.
2.方法归纳:公式法、分类讨论法.
3.常见误区:易忽视实际问题中角的范围.
随堂演练
1.在△ABC中,cos(A+B)的值等于
A.cos C B.-cos C
C.sin C D.-sin C
√
1
2
3
4
由于A+B+C=π,
所以A+B=π-C.
所以cos(A+B)=cos(π-C)=-cos C.
2.已知sin 28°=a,则cos(-602°)等于
√
1
2
3
4
cos(-602°)=cos(2×360°-602°)=cos 118°=cos(90°+28°)=-sin 28°=-a.
A.-2 B.-1 C.1 D.2
1
2
3
4
√
1
2
3
4
本课结束
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
