第五章 §5.7 第2课时 三角函数的应用(二)-高中数学人教A版必修一 课件(共35张PPT)
文档属性
| 名称 | 第五章 §5.7 第2课时 三角函数的应用(二)-高中数学人教A版必修一 课件(共35张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-27 00:00:00 | ||
图片预览











文档简介
(共35张PPT)
第2课时 三角函数的应用(二)
第五章 §5.7 三角函数的应用
1.通过构建三角函数模型解决生活中一些简单的问题.(重点)
2.体会三角函数是描述周期变化现象的重要函数模型.(难点)
学习目标
一、三角函数图象类问题
二、三角函数在生活中的应用
三、三角函数在几何中的应用
随堂演练
内容索引
三角函数图象类问题
一
如图所示,设点A是单位圆上的一定点,动点P从点A出发在圆上按逆时针方向旋转一周,点P所旋转过的 的长为l,弦AP的长为d,则函数d=f(l)的图象大致是
√
例1
设 所对的圆心角为α,则α=l,
故函数d=f(l)的图象大致是选项C的图象.
解决函数图象与实际问题对应问题的策略:一般方法是根据已知所反映出来的性质解决,充分利用图象中的几何关系.此外特殊点也可以作为判断的好方法.
反思感悟
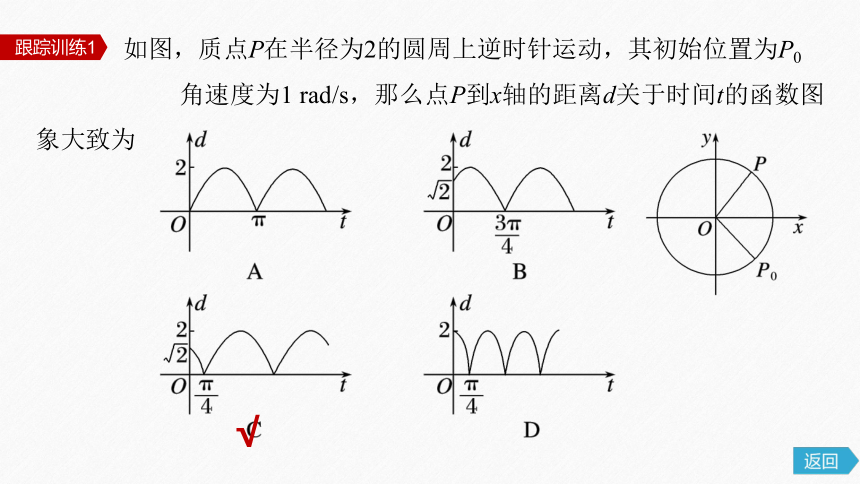
如图,质点P在半径为2的圆周上逆时针运动,其初始位置为P0
角速度为1 rad/s,那么点P到x轴的距离d关于时间t的函数图象大致为
跟踪训练1
√
三角函数在生活中的应用
二
据市场调查,某种商品一年内每月的价格满足函数关系式:f(x)=Asin(ωx+φ)+B ,x为月份.已知3月份该商品的价格首次达到最高,为9万元,7月份该商品的价格首次达到最低,为5万元.
(1)求f(x)的解析式;
例2
(2)求此商品的价格超过8万元的月份.
又1≤x≤12,x∈N*,∴x=2,3,4,10,11,12.
即2月份、3月份、4月份、10月份、11月份、12月份此商品的价格超过8万元.
解三角函数应用问题的基本步骤
反思感悟
通常情况下,同一地区一天的温度随时间变化的曲线接近函数y=Asin(ωx+φ)+b的图象.某年2月下旬某地区连续几天最高温度都出现在14时,最高温度为14 ℃;最低温度出现在凌晨2时,最低温度为零下2 ℃.
(1)求出该地区该时段的温度函数y=Asin(ωx+φ)+b(A>0,ω>0,|φ|<π,x∈[0,24))的解析式;
跟踪训练2
(2)29日上午9时某高中将举行期末考试,如果温度低于10 ℃,教室就要开空调,请问届时学校后勤应该开空调吗?
所以届时学校后勤应该开空调.
三角函数在几何中的应用
三
有一个半径为r,圆心角α= 的扇形铁皮OMN,现利用这块铁皮并根据下列方案之一,裁剪出一个矩形.
例3
方案1:如图1,裁剪出的矩形ABCD的顶点A,B在线段ON上,点C在弧MN上,点D在线段OM上;
方案2:如图2,裁剪出的矩形PQRS的顶点P,S分别在线段OM,ON上,顶点Q,R在弧MN上,并且满足PQ∥RS∥OE,其中点E为弧MN的中点.
(1)按照方案1裁剪,设∠NOC=θ,用θ表示矩形ABCD的面积,并求出其最大面积;
所以矩形ABCD的面积
(2)按照方案2裁剪,求矩形PQRS的最大面积,并与(1)中的结果比较,指出按哪种方案裁剪的矩形面积最大.
所以矩形PQRS的面积
所以按方案1裁剪的矩形面积最大.
反思感悟
利用三角函数解决几何问题,首先要审清题意,然后要明确角的取值范围,最后一定要回归到实际问题当中去.
如图,有一块半径为4的半圆形钢板,计划裁剪成等腰梯形ABCD的形状,它的下底AB是圆O的直径,上底CD的端点在圆周上,连接OC,OC与OB所形成的夹角为θ.
跟踪训练3
(1)写出这个梯形的周长y和θ的函数解析式,并写出它的定义域;
如图,过点C作CE⊥OB,垂足为E.在Rt△OCE和Rt△BCE中,
有OE=4cos θ,CE=4sin θ,DC=2OE=8cos θ.
(2)求周长y的最大值以及此时梯形的面积.
课堂
小结
1.知识清单:
(1)三角函数图象类问题.
(2)三角函数在生活中的应用.
(3)三角函数在几何中的应用.
2.方法归纳:数学建模、数形结合.
3.常见误区:选择三角函数模型时,最后结果忘记回归实际生话.
随堂演练
1.函数y=x+sin |x|,x∈[-π,π]的大致图象是
√
1
2
3
4
2.某艺术展览馆在开馆时间段(9:00-16:00)的参观人数(单位:千)随时间t(单位:时)的变化近似满足函数f(t)=Asin +5(A>0,9≤t≤16),且下午两点整参观人数为7千,则开馆中参观人数的最大值为
A.1万 B.9千 C.8千 D.7千
√
1
2
3
4
由题意知当t=14时,f(t)=7.
3.时钟花是原产于南美热带雨林的藤蔓植物,其开放到闭合与体内的一种时钟酶有关.研究表明,当气温上升到20 ℃时,时钟酶活跃起来,花朵开始开放;当气温上升到28 ℃时,时钟酶的活性减弱,花朵开始闭合,且每天开闭一次.已知某景区一天内5~17时的气温T(单位:℃)与时间t(单位:h)近似满足关系式T=20- 则该景区这天时钟花从开始开放到开始闭合约经历
1
2
3
4
A.1.4 h B.2.4 h
C.3.2 h D.5.6 h
√
1
2
3
4
1
2
3
4
4.某人的血压满足函数式f(t)=24sin 160πt+110,其中f(t)为血压,t为时间,则此人每分钟心跳的次数为_____.
80
本课结束
第2课时 三角函数的应用(二)
第五章 §5.7 三角函数的应用
1.通过构建三角函数模型解决生活中一些简单的问题.(重点)
2.体会三角函数是描述周期变化现象的重要函数模型.(难点)
学习目标
一、三角函数图象类问题
二、三角函数在生活中的应用
三、三角函数在几何中的应用
随堂演练
内容索引
三角函数图象类问题
一
如图所示,设点A是单位圆上的一定点,动点P从点A出发在圆上按逆时针方向旋转一周,点P所旋转过的 的长为l,弦AP的长为d,则函数d=f(l)的图象大致是
√
例1
设 所对的圆心角为α,则α=l,
故函数d=f(l)的图象大致是选项C的图象.
解决函数图象与实际问题对应问题的策略:一般方法是根据已知所反映出来的性质解决,充分利用图象中的几何关系.此外特殊点也可以作为判断的好方法.
反思感悟
如图,质点P在半径为2的圆周上逆时针运动,其初始位置为P0
角速度为1 rad/s,那么点P到x轴的距离d关于时间t的函数图象大致为
跟踪训练1
√
三角函数在生活中的应用
二
据市场调查,某种商品一年内每月的价格满足函数关系式:f(x)=Asin(ωx+φ)+B ,x为月份.已知3月份该商品的价格首次达到最高,为9万元,7月份该商品的价格首次达到最低,为5万元.
(1)求f(x)的解析式;
例2
(2)求此商品的价格超过8万元的月份.
又1≤x≤12,x∈N*,∴x=2,3,4,10,11,12.
即2月份、3月份、4月份、10月份、11月份、12月份此商品的价格超过8万元.
解三角函数应用问题的基本步骤
反思感悟
通常情况下,同一地区一天的温度随时间变化的曲线接近函数y=Asin(ωx+φ)+b的图象.某年2月下旬某地区连续几天最高温度都出现在14时,最高温度为14 ℃;最低温度出现在凌晨2时,最低温度为零下2 ℃.
(1)求出该地区该时段的温度函数y=Asin(ωx+φ)+b(A>0,ω>0,|φ|<π,x∈[0,24))的解析式;
跟踪训练2
(2)29日上午9时某高中将举行期末考试,如果温度低于10 ℃,教室就要开空调,请问届时学校后勤应该开空调吗?
所以届时学校后勤应该开空调.
三角函数在几何中的应用
三
有一个半径为r,圆心角α= 的扇形铁皮OMN,现利用这块铁皮并根据下列方案之一,裁剪出一个矩形.
例3
方案1:如图1,裁剪出的矩形ABCD的顶点A,B在线段ON上,点C在弧MN上,点D在线段OM上;
方案2:如图2,裁剪出的矩形PQRS的顶点P,S分别在线段OM,ON上,顶点Q,R在弧MN上,并且满足PQ∥RS∥OE,其中点E为弧MN的中点.
(1)按照方案1裁剪,设∠NOC=θ,用θ表示矩形ABCD的面积,并求出其最大面积;
所以矩形ABCD的面积
(2)按照方案2裁剪,求矩形PQRS的最大面积,并与(1)中的结果比较,指出按哪种方案裁剪的矩形面积最大.
所以矩形PQRS的面积
所以按方案1裁剪的矩形面积最大.
反思感悟
利用三角函数解决几何问题,首先要审清题意,然后要明确角的取值范围,最后一定要回归到实际问题当中去.
如图,有一块半径为4的半圆形钢板,计划裁剪成等腰梯形ABCD的形状,它的下底AB是圆O的直径,上底CD的端点在圆周上,连接OC,OC与OB所形成的夹角为θ.
跟踪训练3
(1)写出这个梯形的周长y和θ的函数解析式,并写出它的定义域;
如图,过点C作CE⊥OB,垂足为E.在Rt△OCE和Rt△BCE中,
有OE=4cos θ,CE=4sin θ,DC=2OE=8cos θ.
(2)求周长y的最大值以及此时梯形的面积.
课堂
小结
1.知识清单:
(1)三角函数图象类问题.
(2)三角函数在生活中的应用.
(3)三角函数在几何中的应用.
2.方法归纳:数学建模、数形结合.
3.常见误区:选择三角函数模型时,最后结果忘记回归实际生话.
随堂演练
1.函数y=x+sin |x|,x∈[-π,π]的大致图象是
√
1
2
3
4
2.某艺术展览馆在开馆时间段(9:00-16:00)的参观人数(单位:千)随时间t(单位:时)的变化近似满足函数f(t)=Asin +5(A>0,9≤t≤16),且下午两点整参观人数为7千,则开馆中参观人数的最大值为
A.1万 B.9千 C.8千 D.7千
√
1
2
3
4
由题意知当t=14时,f(t)=7.
3.时钟花是原产于南美热带雨林的藤蔓植物,其开放到闭合与体内的一种时钟酶有关.研究表明,当气温上升到20 ℃时,时钟酶活跃起来,花朵开始开放;当气温上升到28 ℃时,时钟酶的活性减弱,花朵开始闭合,且每天开闭一次.已知某景区一天内5~17时的气温T(单位:℃)与时间t(单位:h)近似满足关系式T=20- 则该景区这天时钟花从开始开放到开始闭合约经历
1
2
3
4
A.1.4 h B.2.4 h
C.3.2 h D.5.6 h
√
1
2
3
4
1
2
3
4
4.某人的血压满足函数式f(t)=24sin 160πt+110,其中f(t)为血压,t为时间,则此人每分钟心跳的次数为_____.
80
本课结束
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
