第五章 三角函数 章末复习课-高中数学人教A版必修一 课件(共52张PPT)
文档属性
| 名称 | 第五章 三角函数 章末复习课-高中数学人教A版必修一 课件(共52张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-27 07:06:50 | ||
图片预览









文档简介
(共52张PPT)
章末复习课
第五章 三角函数
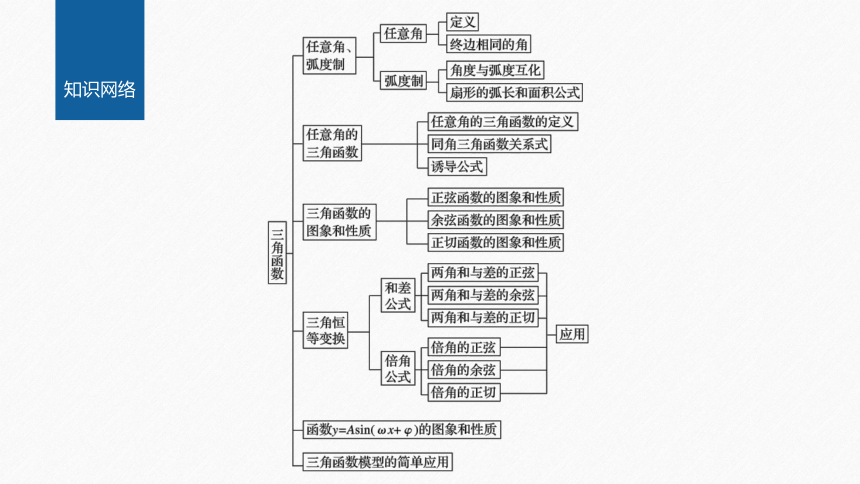
知识网络
一、同角三角函数的基本关系和诱导公式
二、三角函数的图象与性质
三、三角函数的图象变换问题
随堂演练
四、三角恒等变换与三角函数的综合问题
内容索引
同角三角函数的基本关系和诱导公式
一
2.化简三角函数式的常用方法有:(1)直接应用公式;(2)切化弦;(3)异角化同角;(4)特殊值与特殊角的三角函数互化;(5)通分、约分;(6)配方去根号.
3.求值一般包括:(1)给角求值;(2)给值求值;(3)给值求角.
4.掌握三角函数中公式的正用、逆用及变形用,重点提升逻辑推理和数学运算素养.
(1)计算cos 330°等于
√
例1
由诱导公式可得
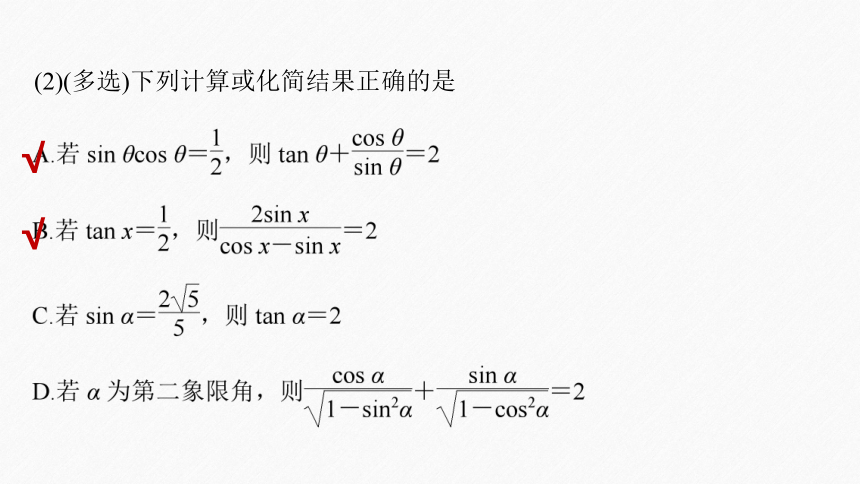
(2)(多选)下列计算或化简结果正确的是
√
√
对于C选项,∵α的范围不确定,∴tan α的符号不确定,故C错误;
应用任意角的三角函数的定义时,注意三角函数值仅与终边位置有关,与终边上的点的位置无关,应用诱导公式时要弄清三角函数值在各个象限内的符号.
反思感悟
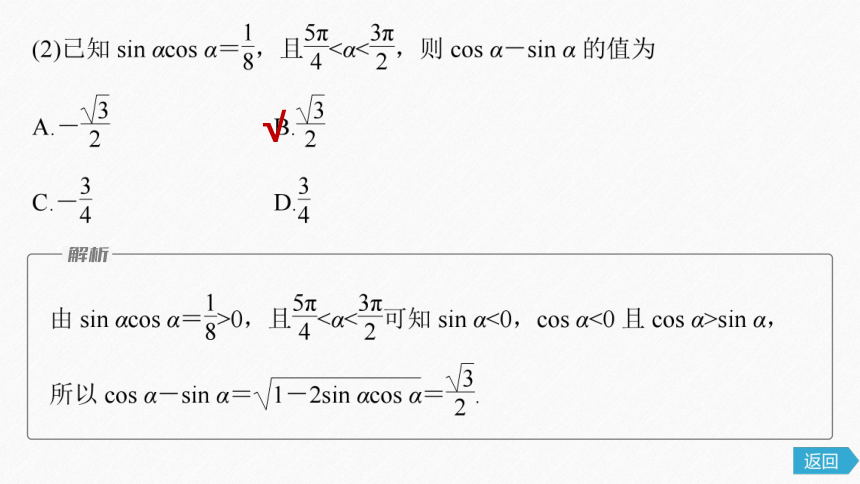
(1)若sin(π-α)>0,tan(π+α)<0,则角α的终边在
A.第一象限 B.第二象限
C.第三象限 D.第四象限
√
跟踪训练1
由题意可知,sin α>0,tan α<0,所以角α的终边在第二象限.
√
三角函数的图象与性质
二
1.三角函数的性质包括定义域、值域、单调性、奇偶性、对称性等,在研究性质时,将ωx+φ看成一个整体,利用整体代换思想解题是常见的技巧.
2.函数y=Asin(ωx+φ)的图象
(1)“五点法”作图;(2)图象伸缩、平移变换.
3.掌握三角函数的图象和性质,重点培养直观想象和数学运算素养.
√
例2
结合三角函数的图象分析三角函数的性质,关键要把f(x)=Asin(ωx+φ)中的ωx+φ看成一个整体,书写时不要漏写k∈Z,注意f(x)图象的对称中心为点的形式.
反思感悟
跟踪训练2
(1)求f(x)的单调区间;
所以f(x)的最大值为2+a+1=4,所以a=1.
三角函数的图象变换问题
三
1.由函数y=sin x的图象得到y=sin(ωx+φ)(ω>0)的图象有两种途径:先平移再伸缩;先伸缩再平移.这两种途径的区别是平移的单位长度不同,其余参数不受影响,若相应变换的函数名称不同时,要先用诱导公式转化为同名的三角函数,再进行平移或伸缩.
2.掌握三角函数图象变换的规则,重点提升逻辑推理和数学运算素养.
在下列三个条件中任选一个,补充在下面的问题中,并作答.
①f(x)的最小正周期为π,且f(x)是偶函数;
例3
(1)求ω,φ的值;(请先在答题卡上写出所选序号再作答)
选条件①:
∵f(x)的最小正周期为π,
又f(x)是偶函数,
得sin 2xcos φ=0对x∈R恒成立,
选条件②:
∵函数f(x)图象上相邻两个最高点之间的距离为π,
选条件③:
又f(0)=2sin φ=2,
反思感悟
函数y=Asin(ωx+φ)+h的解题技巧
对于y=Asin(ωx+φ)+h,应明确A,ω决定“形变”,φ,h决定“位变”,A影响值域,ω影响周期,A,ω,φ影响单调性.针对x的变换,即变换多少个单位长度,向左或向右很容易出错,应注意先“平移”后“伸缩”与先“伸缩”后“平移”的区别.
已知函数f(x)=2sin ,将f(x)的图象向左平移 个单位长度,再将纵坐标缩短到原来的 ,横坐标不变,得到g(x)的图象.
(1)求g(x)的函数解析式;
跟踪训练3
三角恒等变换与三角函数的综合问题
四
1.三角恒等变换与三角函数的综合问题,常以三角恒等变换为主要的化简手段,考查三角函数的性质.当给出的三角函数关系式较为复杂时,我们要先通过三角恒等变换,将三角函数的表达式变形化简为y=Asin(ωx+φ)+k或y=Acos(ωx+φ)+k等形式,然后再根据化简后的三角函数,讨论其图象和性质.
2.通过三角恒等变换,进而研究三角函数的性质,培养逻辑推理和数学运算素养.
(1)求f(x)的解析式;
例3
故f(x)=2sin 2x.
其中θ1+θ2=3π,θ2+θ3=5π,θ3+θ4=7π,θ4+θ5=9π,
反思感悟
解决三角恒等变换与三角函数综合问题的关键在于熟练地运用基本的三角恒等变换思想方法,对其解析式变形、化简,尽量使其化为只有一个角为自变量的三角函数.解决与图象和性质有关的问题,在进行恒等变换时,既要注意三角恒等交换思想(切化弦、常值代换、降幂与升幂、收缩代换、和差与积的互化、角的代换)的运用,还要注意一般的数学思想方法(如换元法等)的运用.
跟踪训练4
将y=f(x)的图象向左平移m(m>0)个单位长度,
随堂演练
1.若圆弧长度等于圆内接正三角形的边长,则其圆心角的弧度数为
√
1
2
3
4
如图,等边三角形ABC是半径为r的圆O的内接三角形,则线段AB所对的圆心角∠AOB=
1
2
3
4
过点O作OM⊥AB,垂足为M.
√
1
2
3
4
√
1
2
3
4
√
√
1
2
3
4
1
2
3
4
本课结束
章末复习课
第五章 三角函数
知识网络
一、同角三角函数的基本关系和诱导公式
二、三角函数的图象与性质
三、三角函数的图象变换问题
随堂演练
四、三角恒等变换与三角函数的综合问题
内容索引
同角三角函数的基本关系和诱导公式
一
2.化简三角函数式的常用方法有:(1)直接应用公式;(2)切化弦;(3)异角化同角;(4)特殊值与特殊角的三角函数互化;(5)通分、约分;(6)配方去根号.
3.求值一般包括:(1)给角求值;(2)给值求值;(3)给值求角.
4.掌握三角函数中公式的正用、逆用及变形用,重点提升逻辑推理和数学运算素养.
(1)计算cos 330°等于
√
例1
由诱导公式可得
(2)(多选)下列计算或化简结果正确的是
√
√
对于C选项,∵α的范围不确定,∴tan α的符号不确定,故C错误;
应用任意角的三角函数的定义时,注意三角函数值仅与终边位置有关,与终边上的点的位置无关,应用诱导公式时要弄清三角函数值在各个象限内的符号.
反思感悟
(1)若sin(π-α)>0,tan(π+α)<0,则角α的终边在
A.第一象限 B.第二象限
C.第三象限 D.第四象限
√
跟踪训练1
由题意可知,sin α>0,tan α<0,所以角α的终边在第二象限.
√
三角函数的图象与性质
二
1.三角函数的性质包括定义域、值域、单调性、奇偶性、对称性等,在研究性质时,将ωx+φ看成一个整体,利用整体代换思想解题是常见的技巧.
2.函数y=Asin(ωx+φ)的图象
(1)“五点法”作图;(2)图象伸缩、平移变换.
3.掌握三角函数的图象和性质,重点培养直观想象和数学运算素养.
√
例2
结合三角函数的图象分析三角函数的性质,关键要把f(x)=Asin(ωx+φ)中的ωx+φ看成一个整体,书写时不要漏写k∈Z,注意f(x)图象的对称中心为点的形式.
反思感悟
跟踪训练2
(1)求f(x)的单调区间;
所以f(x)的最大值为2+a+1=4,所以a=1.
三角函数的图象变换问题
三
1.由函数y=sin x的图象得到y=sin(ωx+φ)(ω>0)的图象有两种途径:先平移再伸缩;先伸缩再平移.这两种途径的区别是平移的单位长度不同,其余参数不受影响,若相应变换的函数名称不同时,要先用诱导公式转化为同名的三角函数,再进行平移或伸缩.
2.掌握三角函数图象变换的规则,重点提升逻辑推理和数学运算素养.
在下列三个条件中任选一个,补充在下面的问题中,并作答.
①f(x)的最小正周期为π,且f(x)是偶函数;
例3
(1)求ω,φ的值;(请先在答题卡上写出所选序号再作答)
选条件①:
∵f(x)的最小正周期为π,
又f(x)是偶函数,
得sin 2xcos φ=0对x∈R恒成立,
选条件②:
∵函数f(x)图象上相邻两个最高点之间的距离为π,
选条件③:
又f(0)=2sin φ=2,
反思感悟
函数y=Asin(ωx+φ)+h的解题技巧
对于y=Asin(ωx+φ)+h,应明确A,ω决定“形变”,φ,h决定“位变”,A影响值域,ω影响周期,A,ω,φ影响单调性.针对x的变换,即变换多少个单位长度,向左或向右很容易出错,应注意先“平移”后“伸缩”与先“伸缩”后“平移”的区别.
已知函数f(x)=2sin ,将f(x)的图象向左平移 个单位长度,再将纵坐标缩短到原来的 ,横坐标不变,得到g(x)的图象.
(1)求g(x)的函数解析式;
跟踪训练3
三角恒等变换与三角函数的综合问题
四
1.三角恒等变换与三角函数的综合问题,常以三角恒等变换为主要的化简手段,考查三角函数的性质.当给出的三角函数关系式较为复杂时,我们要先通过三角恒等变换,将三角函数的表达式变形化简为y=Asin(ωx+φ)+k或y=Acos(ωx+φ)+k等形式,然后再根据化简后的三角函数,讨论其图象和性质.
2.通过三角恒等变换,进而研究三角函数的性质,培养逻辑推理和数学运算素养.
(1)求f(x)的解析式;
例3
故f(x)=2sin 2x.
其中θ1+θ2=3π,θ2+θ3=5π,θ3+θ4=7π,θ4+θ5=9π,
反思感悟
解决三角恒等变换与三角函数综合问题的关键在于熟练地运用基本的三角恒等变换思想方法,对其解析式变形、化简,尽量使其化为只有一个角为自变量的三角函数.解决与图象和性质有关的问题,在进行恒等变换时,既要注意三角恒等交换思想(切化弦、常值代换、降幂与升幂、收缩代换、和差与积的互化、角的代换)的运用,还要注意一般的数学思想方法(如换元法等)的运用.
跟踪训练4
将y=f(x)的图象向左平移m(m>0)个单位长度,
随堂演练
1.若圆弧长度等于圆内接正三角形的边长,则其圆心角的弧度数为
√
1
2
3
4
如图,等边三角形ABC是半径为r的圆O的内接三角形,则线段AB所对的圆心角∠AOB=
1
2
3
4
过点O作OM⊥AB,垂足为M.
√
1
2
3
4
√
1
2
3
4
√
√
1
2
3
4
1
2
3
4
本课结束
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
