【全国百强校】广东省广州市第六中学高中数学人教版必修三2统计复习课 课件(共24张PPT)
文档属性
| 名称 | 【全国百强校】广东省广州市第六中学高中数学人教版必修三2统计复习课 课件(共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 690.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-08-21 07:25:35 | ||
图片预览







文档简介
课件24张PPT。第二章 统 计
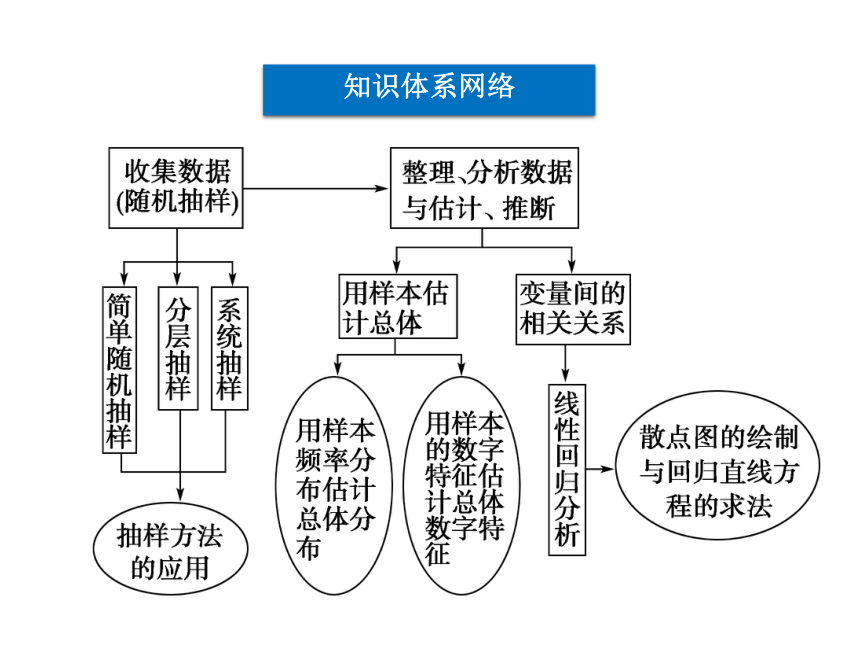
复习课知识体系网络专题探究精讲三种抽样方法应用原则
1.当总体容量较小,样本容量也较小时,制签简单,号签容易搅匀,可采用抽签法;
2.当总体容量较大,样本容量较小时,可用随机数表法;
3.当总体容量较大,样本容量也较大时,可用系统抽样法;
4.当总体由有明显差异的几部分构成时,采用分层抽样法. 一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆):按类用分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆.
(1)求z的值;
(2)B类,C类轿车各应抽取多少?
(3)在C类轿车中,按型号分层抽样,应各抽取多少?
【思路点拨】 按类分层或者是按型号分层,抽样比是相同的.课内练习系列1
(1)将参加夏令营的600名学生编号为:001,002,…,600.采用系统抽样方法抽取一个容量为50的样本,且在第一段中随机抽得的号码是003.这600名学生分别住在三个营区,从001到300在第一营区,从301到495在第二营区,从496到600在第三营区.则三个营区被抽到的人数分别为( )
A.25,17,8 B.25,16,9 C.26,16,8 D.24,17,9(2)某校高一年级有x个学生,高二年级有900个学生,高三年级有y个学生,采用分层抽样抽一个容量为370的样本,高一年级抽取120人,高三年级抽取100人,则高一有_______学生B720利用样本的频率分布表和频率分布直方图对总体情况作出估计,有时也利用频率分布折线图和茎叶图对总体估计.
1.用样本频率分布估计总体频率分布时,通常要对给定的一组数据进行列表、作图处理,作频率分布表与频率分布直方图时要注意其方法步骤.
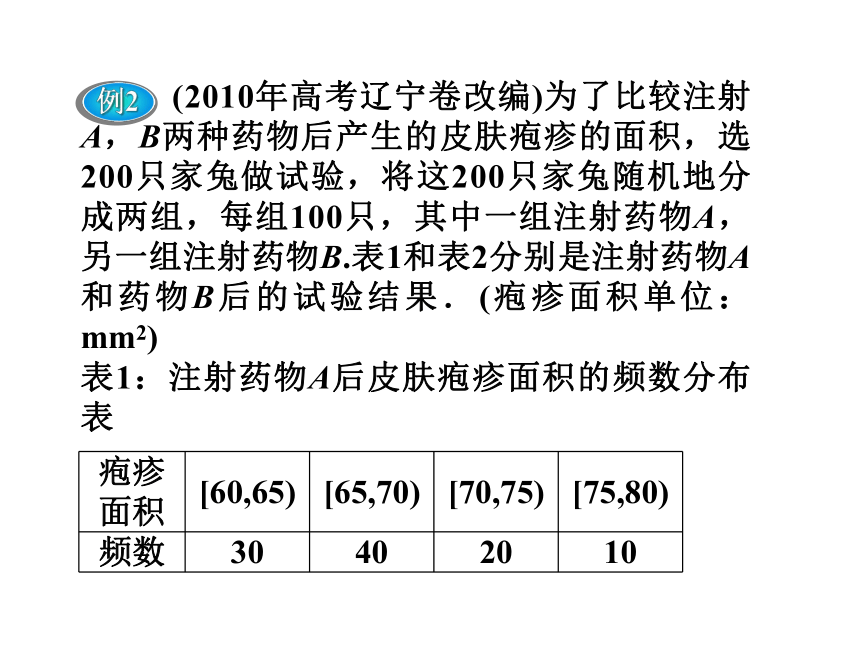
2.茎叶图刻画数据有两个优点:一是所有信息都可以从图中得到,二是便于记录和表示,但数据较多时不方便. (2010年高考辽宁卷改编)为了比较注射A,B两种药物后产生的皮肤疱疹的面积,选200只家兔做试验,将这200只家兔随机地分成两组,每组100只,其中一组注射药物A,另一组注射药物B.表1和表2分别是注射药物A和药物B后的试验结果.(疱疹面积单位:mm2)
表1:注射药物A后皮肤疱疹面积的频数分布表表2:注射药物B后皮肤疱疹面积的频数分布表完成下面频率分布直方图,并比较注射两种药物后疱疹面积的中位数大小.
注射药物A后皮肤疱疹面积的
频率分布直方图注射药物B后皮肤疱疹
面积的频率分布直方图可以看出注射药物A后的疱疹面积的中位数在65至70之间,而注射药物B后的疱疹面积的中位数在70至75之间,所以注射药物A后疱疹面积的中位数小于注射药物B后疱疹面积的中位数.
【思维总结】 在直方图中,利用中位数两侧的面积相等来估计中位数.0.033115124.5样本的数字特征可分为两大类:一类是反映样本数据集中趋势的,包括众数、中位数和平均数;另一类是反映样本波动大小的,包括方差及标准差.我们常通过样本的数字特征估计总体的数字特征. (2009广东卷)随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图7
(1)根据茎叶图判断哪个班的平均身高较高;
(2)计算甲班的样本方差
(3)从茎叶图中判断哪个班
的学生身高情况更稳定(1)甲班平均身高为170cm;乙班171.1(也可以根据数据分布来观察,乙班170以上的人较多,160~170人较少,故乙班平均身高会高一点(2)甲的方差:(3)对比两者平均数及从茎叶图中数据的分布情况,乙的数据波动相对大,故甲的数据较为稳定除了函数关系这种确定性的关系外,还有大量因变量的取值带有一定随机性的两个变量之间的关系——相关关系.应用回归直线方程可分析具有线性相关的两个变量之间的关系. 假设关于某设备的使用年限x和所支出的维修费用y(万元)有如下的统计资料:(1)作出散点图,判断y对x是否成线性相关,若线性相关,求线性回归方程=bx+a的回归系数a,b;
(2)估计使用年限为10年时的维修费用.
?
【思路点拨】 作出散点图,观察两变量是否线性相关,若相关,利用公式求出a,b.【解】 (1)作出散点图,如图所示,由散点图可知y对x是线性相关的.制表【思维总结】 知道x与y呈线性相关关系,无需进行相关性检测,否则,应首先进行相关性检验,如果本身两个变量不具备相关关系,或者说,它们之间相关关系不显著,即使求出回归直线方程也是毫无意义,而且用其估计和预测的量也是不可信的.
复习课知识体系网络专题探究精讲三种抽样方法应用原则
1.当总体容量较小,样本容量也较小时,制签简单,号签容易搅匀,可采用抽签法;
2.当总体容量较大,样本容量较小时,可用随机数表法;
3.当总体容量较大,样本容量也较大时,可用系统抽样法;
4.当总体由有明显差异的几部分构成时,采用分层抽样法. 一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆):按类用分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆.
(1)求z的值;
(2)B类,C类轿车各应抽取多少?
(3)在C类轿车中,按型号分层抽样,应各抽取多少?
【思路点拨】 按类分层或者是按型号分层,抽样比是相同的.课内练习系列1
(1)将参加夏令营的600名学生编号为:001,002,…,600.采用系统抽样方法抽取一个容量为50的样本,且在第一段中随机抽得的号码是003.这600名学生分别住在三个营区,从001到300在第一营区,从301到495在第二营区,从496到600在第三营区.则三个营区被抽到的人数分别为( )
A.25,17,8 B.25,16,9 C.26,16,8 D.24,17,9(2)某校高一年级有x个学生,高二年级有900个学生,高三年级有y个学生,采用分层抽样抽一个容量为370的样本,高一年级抽取120人,高三年级抽取100人,则高一有_______学生B720利用样本的频率分布表和频率分布直方图对总体情况作出估计,有时也利用频率分布折线图和茎叶图对总体估计.
1.用样本频率分布估计总体频率分布时,通常要对给定的一组数据进行列表、作图处理,作频率分布表与频率分布直方图时要注意其方法步骤.
2.茎叶图刻画数据有两个优点:一是所有信息都可以从图中得到,二是便于记录和表示,但数据较多时不方便. (2010年高考辽宁卷改编)为了比较注射A,B两种药物后产生的皮肤疱疹的面积,选200只家兔做试验,将这200只家兔随机地分成两组,每组100只,其中一组注射药物A,另一组注射药物B.表1和表2分别是注射药物A和药物B后的试验结果.(疱疹面积单位:mm2)
表1:注射药物A后皮肤疱疹面积的频数分布表表2:注射药物B后皮肤疱疹面积的频数分布表完成下面频率分布直方图,并比较注射两种药物后疱疹面积的中位数大小.
注射药物A后皮肤疱疹面积的
频率分布直方图注射药物B后皮肤疱疹
面积的频率分布直方图可以看出注射药物A后的疱疹面积的中位数在65至70之间,而注射药物B后的疱疹面积的中位数在70至75之间,所以注射药物A后疱疹面积的中位数小于注射药物B后疱疹面积的中位数.
【思维总结】 在直方图中,利用中位数两侧的面积相等来估计中位数.0.033115124.5样本的数字特征可分为两大类:一类是反映样本数据集中趋势的,包括众数、中位数和平均数;另一类是反映样本波动大小的,包括方差及标准差.我们常通过样本的数字特征估计总体的数字特征. (2009广东卷)随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图7
(1)根据茎叶图判断哪个班的平均身高较高;
(2)计算甲班的样本方差
(3)从茎叶图中判断哪个班
的学生身高情况更稳定(1)甲班平均身高为170cm;乙班171.1(也可以根据数据分布来观察,乙班170以上的人较多,160~170人较少,故乙班平均身高会高一点(2)甲的方差:(3)对比两者平均数及从茎叶图中数据的分布情况,乙的数据波动相对大,故甲的数据较为稳定除了函数关系这种确定性的关系外,还有大量因变量的取值带有一定随机性的两个变量之间的关系——相关关系.应用回归直线方程可分析具有线性相关的两个变量之间的关系. 假设关于某设备的使用年限x和所支出的维修费用y(万元)有如下的统计资料:(1)作出散点图,判断y对x是否成线性相关,若线性相关,求线性回归方程=bx+a的回归系数a,b;
(2)估计使用年限为10年时的维修费用.
?
【思路点拨】 作出散点图,观察两变量是否线性相关,若相关,利用公式求出a,b.【解】 (1)作出散点图,如图所示,由散点图可知y对x是线性相关的.制表【思维总结】 知道x与y呈线性相关关系,无需进行相关性检测,否则,应首先进行相关性检验,如果本身两个变量不具备相关关系,或者说,它们之间相关关系不显著,即使求出回归直线方程也是毫无意义,而且用其估计和预测的量也是不可信的.
