【全国百强校】广东省广州市第六中学高中数学人教版必修三3.1 随机事件的概率 课件(共35张PPT)
文档属性
| 名称 | 【全国百强校】广东省广州市第六中学高中数学人教版必修三3.1 随机事件的概率 课件(共35张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-08-21 00:00:00 | ||
图片预览










文档简介
课件35张PPT。第三章 概 率3.1 随机事件的概率
3.1.1 随机事件的概率1.夜深知雪重,时闻折竹声.2009年11月12日夜起,泉城济南迎来了5年来最大的一场降雪.一夜之间,初入寒冬的泉城银装素裹,犹如童话中的冰雪世界.伴随着此次降雪,全市的气温明显降低.
你能推测出明年11月12日济南会下雪吗?2.我们来看下面一些事件:
(1)“抛一块石头,下落”;
(2)“标准大气压下且温度低于0 ℃时,冰融化”;
(3)“上海七月下雪”;
(4)“下周一某地的最高气温与最低气温相差10 ℃”;
(5)“掷一枚骰子,出现6点”,上面事件发生与否,各有什么特点?1.事件的概念及分类一定不会发生一定会发生可能发生也可能不发生nA3.概率
(1)含义:概率是度量随机事件发生的___________ 的量.
(2)与频率联系:对于给定的随机事件A,事件A发 生的_________随着试验次数的增加稳定于_____ _____,因此可以用___________来估计__________.可能性大小频率fn(A)概率P(A)频率fn(A)概率P(A)1.下面五个事件:
(1)某年4月日本发生大地震;(2)函数y=ax(a>0且a≠1)在定义域上是增函数;(3)实数的绝对值不小于0;(4)在标准大气压下,水在1 ℃结冰;(5)a,b∈R,则ab=ba,其中必然事件是( )
A.(3)(5) B.(2)(3)(4)
C.(1)(2) D.(2)(5)
解析: 必然事件是指一定会发生的事件.(1)(2)为随机事件,(4)为不可能事件,(3)(5)为必然事件.
答案: A2.下列事件中,是随机事件的是( )
A.长度为3,4,5的三条线段可以构成一个三角形
B.长度为2,3,4的三条线段可以构成一直角三角形
C.方程x2+2x+3=0有两个不相等的实根
D.美国发射航天飞机成功
解析: A为必然事件,B,C为不可能事件,D为随机事件.故选D.
答案: D3.下列试验不能构成事件的是________(填序号).
①掷一次硬币;②射击一次;③标准大气压下,水烧至100 ℃;④摸彩票中头奖.
解析: 每一次试验连同它产生的结果叫做事件.①②③只是试验,没有结果,故不叫事件.④既有试验又有结果,故是事件.
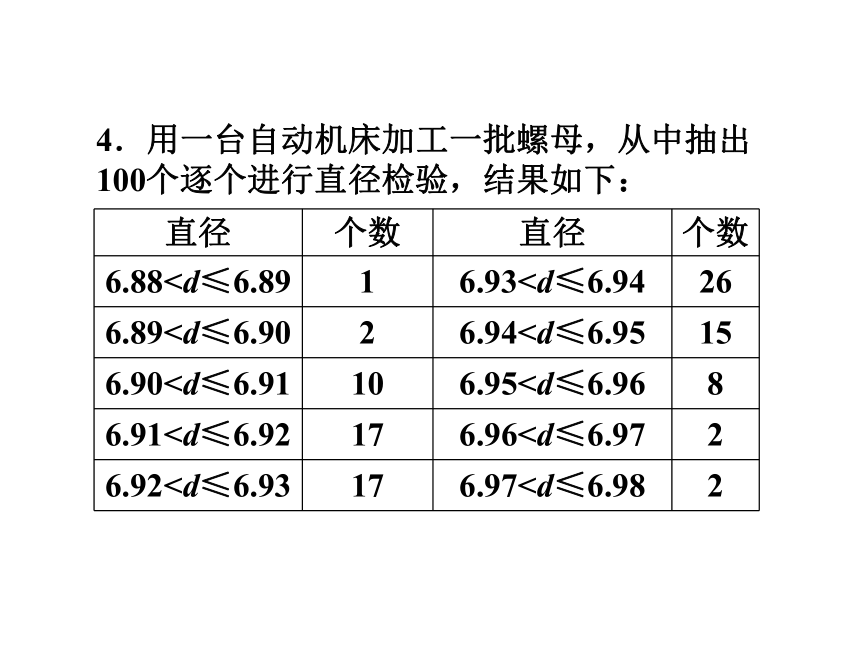
答案: ①②③4.用一台自动机床加工一批螺母,从中抽出100个逐个进行直径检验,结果如下:从这100个螺母中任意抽取一个,求:
(1)事件A(6.92(2)事件B(6.90(3)事件C(d>6.96)的频率;
(4)事件D(d≤6.89)的频率.(3)某人给其朋友打电话,却忘记了朋友电话号码的最后一个数字,就随意在键盘上按了一个数字,恰巧是朋友的电话号码;
(4)如果a,b都是实数,那么a+b=b+a;
(5)一个正六面体的六个面分别写有数字1,2,3,4,5,6,将它连掷2次,数字之和大于12.[解题过程] [题后感悟] 在进行事件的判定时,应注意:
(1)条件的不同与变化都将影响事件的发生或其结果,要注意从问题的背景中体会条件的特点.
(2)必然事件具有确定性,它在一定条件下肯定发生,随机事件可作以下解释:在相同的条件下观察试验,每一次的试验结果不一定相同,且无法预测下一次试验结果是什么. (4)“从分别标有号数1,2,3,4,5的5张标签中任取一张,得到4号签”;
(5)“某电话机在1分钟内收到2次呼叫”;
(6)“没有水分,种子发芽”.
解析: 根据它们的定义判断.(3)、(6)是不可能事件,(1)、(2)、(4)、(5)是随机事件.[规范解答] (1)结果:红球,白球;红球,黑球;白球,黑球.4分
(2)结果:
1-3=-2,3-1=2,
1-6=-5,3-6=-3,
1-10=-9,3-10=-7,
6-1=5,10-1=9,
6-3=3,10-3=7,
6-10=-4,10-6=4.12分[题后感悟] 准确理解随机试验的条件、结果等有关定义,并能使用它们判断一些事件,指出试验结果,这是求概率的基础.在写试验结果时,一般采用列举法写出,必须首先明确事件发生的条件,根据日常生活经验,按一定次序列举,才能保证所列结果没有重复,也没有遗漏.解析: (1)当x=1时,y=2,3,4;当x=2时,y=1,3,4;同理,当x分别为3,4时,也各有3个不同的y,所以共有12个不同的有序数对.故这个试验结果的种数为12.
(2)记“第一次取出的小球上的数字是2”为事件A,则A={(2,1),(2,3),(2,4)}.[策略点睛]解析: (1)进球的频率依次是0.75,0.80,0.75,0.78,0.70,0.75.
(2)这位运动员投篮一次进球的概率P≈0.76.1.随机试验
如果一个试验满足以下条件
(1)试验可以在相同的条件下重复进行;
(2)试验的所有结果是明确可知的,但不止一个;
(3)每次试验总是出现这些结果中的一个,但在试验之前却不能确定会出现哪一个结果.
则这样的试验叫做随机试验.2.频数、频率和概率间的关系
(1)频数是指在n次重复试验中事件A出现的次数,频率是频数与试验总次数的比值,而概率是随机事件发生的可能性的规律体现.
(2)随机事件的频率在每次试验中都可能会有不同的结果,但它具有一定的稳定性,概率是频率的稳定值,是频率的科学抽象,不会随试验次数的变化而变化.
3.对于概率的定义必须注意以下三点
(1)频率与概率有本质的区别,频率随着试验次数的改变而变化,概率却是一个常数,它是频率的科学抽象.当试验次数越来越多时频率向概率靠近.(2)在试验应用中,只要次数足够多,所得频率就近似地当作随机事件的概率.
(3)概率意义下的“可能性”是大量随机事件现象的客观规律,与我们日常所说的“可能”“估计”是不同的,也就是说,单独一次结果的不肯定性与积累结果的有规律性,才是概率意义下的“可能性”,事件A的概率是事件A的本质属性.◎先后抛掷两枚质地均匀的硬币,则
(1)一共可能出现多少种不同的结果?
(2)出现“一枚正面,另一枚反面”的情况分几种?
【错解】 (1)一共可能出现“两枚正面”“两枚反面”“一枚正面,一枚反面”,3种不同情况.
(2)出现“一枚正面,一枚反面”的结果只有一种.【错因】 将“一正,一反”“一反,一正”两种情形错认为是“一正,一反”一种情形,忽视了“先后”这个关键词,在题干中若强调了“先后”“依次”“顺序”“前后”,就必须注意顺序问题.
【正解】 (1)一共可能出现“两枚正面”“两枚反面”“一枚正面,一枚反面”“一枚反面,一枚正面”,4种不同的结果.
(2)出现“一枚正面,另一枚反面”的情况有2种.
3.1.1 随机事件的概率1.夜深知雪重,时闻折竹声.2009年11月12日夜起,泉城济南迎来了5年来最大的一场降雪.一夜之间,初入寒冬的泉城银装素裹,犹如童话中的冰雪世界.伴随着此次降雪,全市的气温明显降低.
你能推测出明年11月12日济南会下雪吗?2.我们来看下面一些事件:
(1)“抛一块石头,下落”;
(2)“标准大气压下且温度低于0 ℃时,冰融化”;
(3)“上海七月下雪”;
(4)“下周一某地的最高气温与最低气温相差10 ℃”;
(5)“掷一枚骰子,出现6点”,上面事件发生与否,各有什么特点?1.事件的概念及分类一定不会发生一定会发生可能发生也可能不发生nA3.概率
(1)含义:概率是度量随机事件发生的___________ 的量.
(2)与频率联系:对于给定的随机事件A,事件A发 生的_________随着试验次数的增加稳定于_____ _____,因此可以用___________来估计__________.可能性大小频率fn(A)概率P(A)频率fn(A)概率P(A)1.下面五个事件:
(1)某年4月日本发生大地震;(2)函数y=ax(a>0且a≠1)在定义域上是增函数;(3)实数的绝对值不小于0;(4)在标准大气压下,水在1 ℃结冰;(5)a,b∈R,则ab=ba,其中必然事件是( )
A.(3)(5) B.(2)(3)(4)
C.(1)(2) D.(2)(5)
解析: 必然事件是指一定会发生的事件.(1)(2)为随机事件,(4)为不可能事件,(3)(5)为必然事件.
答案: A2.下列事件中,是随机事件的是( )
A.长度为3,4,5的三条线段可以构成一个三角形
B.长度为2,3,4的三条线段可以构成一直角三角形
C.方程x2+2x+3=0有两个不相等的实根
D.美国发射航天飞机成功
解析: A为必然事件,B,C为不可能事件,D为随机事件.故选D.
答案: D3.下列试验不能构成事件的是________(填序号).
①掷一次硬币;②射击一次;③标准大气压下,水烧至100 ℃;④摸彩票中头奖.
解析: 每一次试验连同它产生的结果叫做事件.①②③只是试验,没有结果,故不叫事件.④既有试验又有结果,故是事件.
答案: ①②③4.用一台自动机床加工一批螺母,从中抽出100个逐个进行直径检验,结果如下:从这100个螺母中任意抽取一个,求:
(1)事件A(6.92
(4)事件D(d≤6.89)的频率.(3)某人给其朋友打电话,却忘记了朋友电话号码的最后一个数字,就随意在键盘上按了一个数字,恰巧是朋友的电话号码;
(4)如果a,b都是实数,那么a+b=b+a;
(5)一个正六面体的六个面分别写有数字1,2,3,4,5,6,将它连掷2次,数字之和大于12.[解题过程] [题后感悟] 在进行事件的判定时,应注意:
(1)条件的不同与变化都将影响事件的发生或其结果,要注意从问题的背景中体会条件的特点.
(2)必然事件具有确定性,它在一定条件下肯定发生,随机事件可作以下解释:在相同的条件下观察试验,每一次的试验结果不一定相同,且无法预测下一次试验结果是什么. (4)“从分别标有号数1,2,3,4,5的5张标签中任取一张,得到4号签”;
(5)“某电话机在1分钟内收到2次呼叫”;
(6)“没有水分,种子发芽”.
解析: 根据它们的定义判断.(3)、(6)是不可能事件,(1)、(2)、(4)、(5)是随机事件.[规范解答] (1)结果:红球,白球;红球,黑球;白球,黑球.4分
(2)结果:
1-3=-2,3-1=2,
1-6=-5,3-6=-3,
1-10=-9,3-10=-7,
6-1=5,10-1=9,
6-3=3,10-3=7,
6-10=-4,10-6=4.12分[题后感悟] 准确理解随机试验的条件、结果等有关定义,并能使用它们判断一些事件,指出试验结果,这是求概率的基础.在写试验结果时,一般采用列举法写出,必须首先明确事件发生的条件,根据日常生活经验,按一定次序列举,才能保证所列结果没有重复,也没有遗漏.解析: (1)当x=1时,y=2,3,4;当x=2时,y=1,3,4;同理,当x分别为3,4时,也各有3个不同的y,所以共有12个不同的有序数对.故这个试验结果的种数为12.
(2)记“第一次取出的小球上的数字是2”为事件A,则A={(2,1),(2,3),(2,4)}.[策略点睛]解析: (1)进球的频率依次是0.75,0.80,0.75,0.78,0.70,0.75.
(2)这位运动员投篮一次进球的概率P≈0.76.1.随机试验
如果一个试验满足以下条件
(1)试验可以在相同的条件下重复进行;
(2)试验的所有结果是明确可知的,但不止一个;
(3)每次试验总是出现这些结果中的一个,但在试验之前却不能确定会出现哪一个结果.
则这样的试验叫做随机试验.2.频数、频率和概率间的关系
(1)频数是指在n次重复试验中事件A出现的次数,频率是频数与试验总次数的比值,而概率是随机事件发生的可能性的规律体现.
(2)随机事件的频率在每次试验中都可能会有不同的结果,但它具有一定的稳定性,概率是频率的稳定值,是频率的科学抽象,不会随试验次数的变化而变化.
3.对于概率的定义必须注意以下三点
(1)频率与概率有本质的区别,频率随着试验次数的改变而变化,概率却是一个常数,它是频率的科学抽象.当试验次数越来越多时频率向概率靠近.(2)在试验应用中,只要次数足够多,所得频率就近似地当作随机事件的概率.
(3)概率意义下的“可能性”是大量随机事件现象的客观规律,与我们日常所说的“可能”“估计”是不同的,也就是说,单独一次结果的不肯定性与积累结果的有规律性,才是概率意义下的“可能性”,事件A的概率是事件A的本质属性.◎先后抛掷两枚质地均匀的硬币,则
(1)一共可能出现多少种不同的结果?
(2)出现“一枚正面,另一枚反面”的情况分几种?
【错解】 (1)一共可能出现“两枚正面”“两枚反面”“一枚正面,一枚反面”,3种不同情况.
(2)出现“一枚正面,一枚反面”的结果只有一种.【错因】 将“一正,一反”“一反,一正”两种情形错认为是“一正,一反”一种情形,忽视了“先后”这个关键词,在题干中若强调了“先后”“依次”“顺序”“前后”,就必须注意顺序问题.
【正解】 (1)一共可能出现“两枚正面”“两枚反面”“一枚正面,一枚反面”“一枚反面,一枚正面”,4种不同的结果.
(2)出现“一枚正面,另一枚反面”的情况有2种.
