【全国百强校】广东省广州市第六中学高中数学人教版必修三232 两个变量的线性关系 课件(共17张PPT)
文档属性
| 名称 | 【全国百强校】广东省广州市第六中学高中数学人教版必修三232 两个变量的线性关系 课件(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 235.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-08-21 07:30:31 | ||
图片预览



文档简介
课件17张PPT。2.3.2 两个变量的线性关系.复习引入: 1、前面我们学习了现实生活中存在许多相关关系:商品销售与广告、粮食生产与施肥量、人体的脂肪量与年龄等等的相关关系.
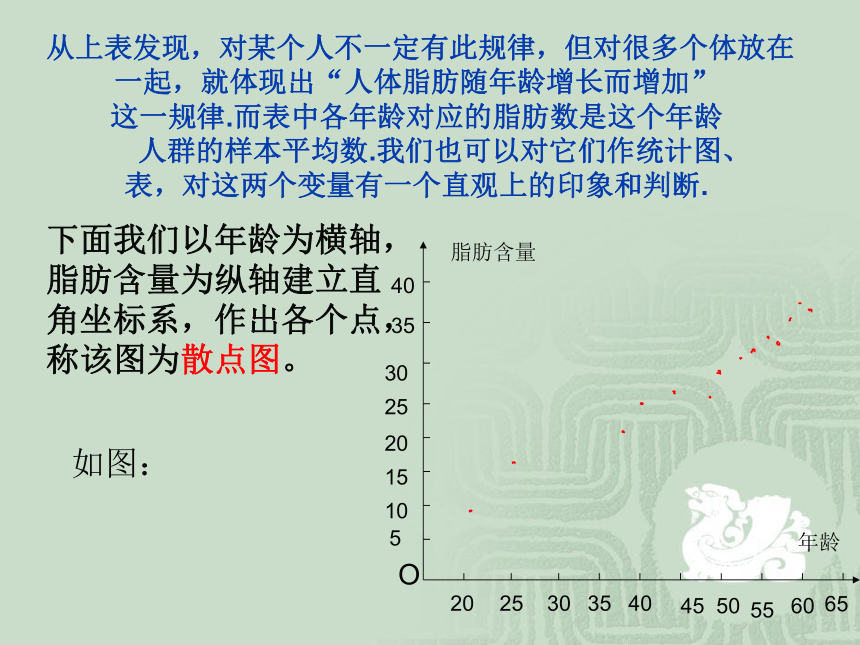
2、通过收集大量的数据,进行统计,对数据分析,找出其中的规律,对其相关关系作出一定判断. 3、由于变量之间相关关系的广泛性和不确定性,所以样本数据应较大,和有代表性.才能对它们之间的关系作出正确的判断. 从上表发现,对某个人不一定有此规律,但对很多个体放在一起,就体现出“人体脂肪随年龄增长而增加” 这一规律.而表中各年龄对应的脂肪数是这个年龄 人群的样本平均数.我们也可以对它们作统计图、 表,对这两个变量有一个直观上的印象和判断. 下面我们以年龄为横轴,
脂肪含量为纵轴建立直
角坐标系,作出各个点,
称该图为散点图。如图:O20253035404550556065年龄脂肪含量510152025303540我们再观察它的图像发现这些点大致分布在一条直线附 近,像这样,如果散点图中点的分布从整体上看大致在 一条直线附近,我们就称这两个变量之间具有线性相 关关系,这条直线叫做回归直线,该直线叫回归方程。 那么,我们该怎样来求出这个回归方程?
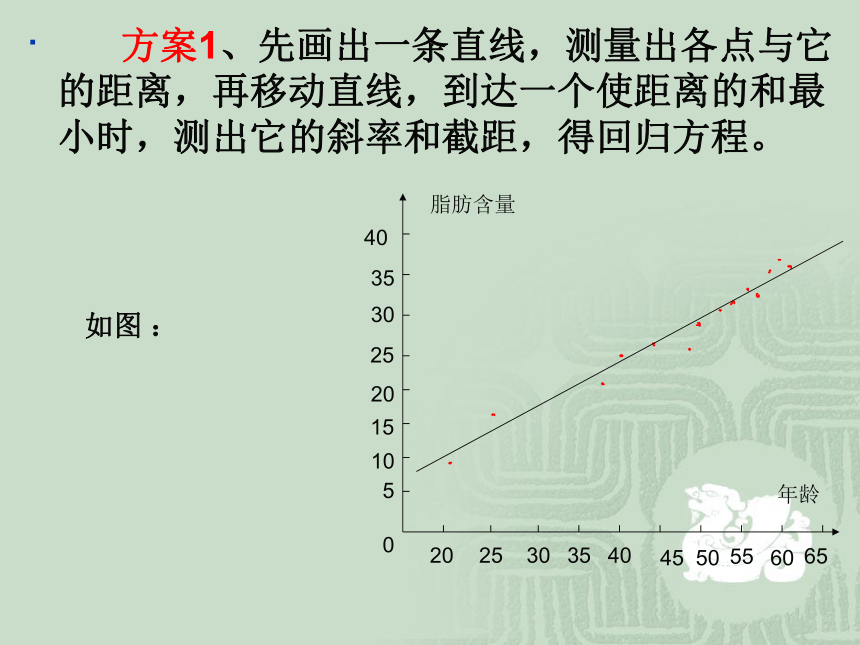
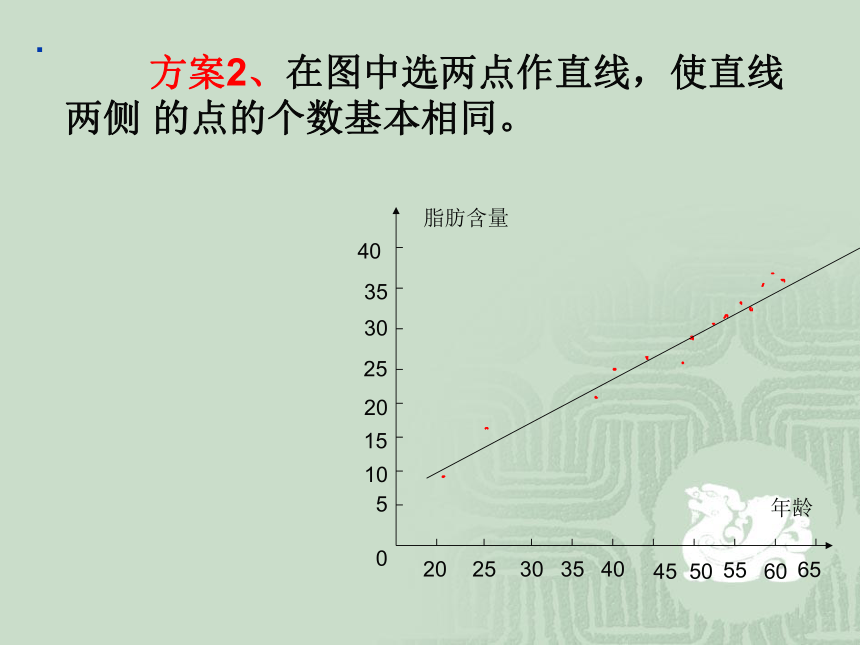
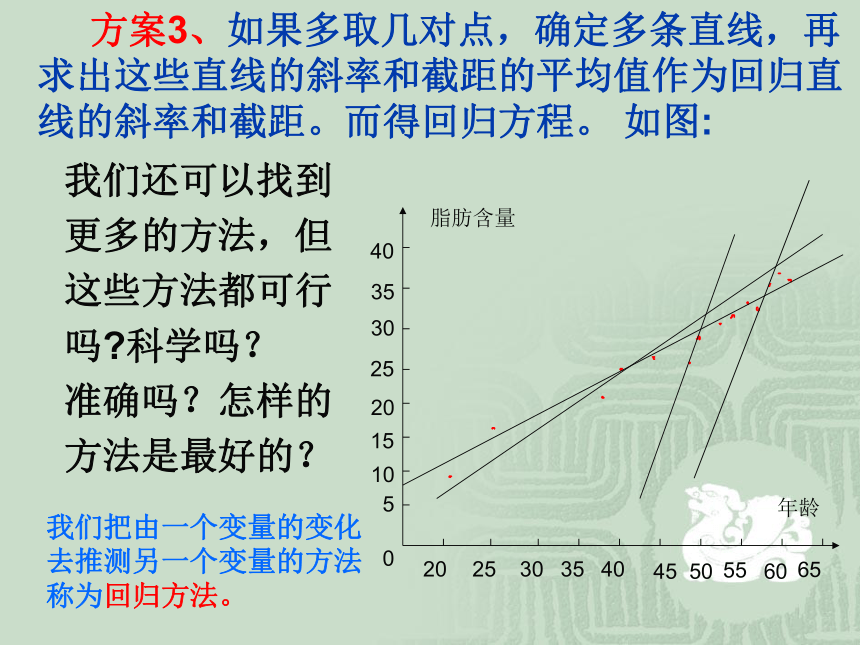
请同学们展开讨论,能得出哪些具体的方案?20253035404550556065年龄脂肪含量0510152025303540. 方案1、先画出一条直线,测量出各点与它的距离,再移动直线,到达一个使距离的和最小时,测出它的斜率和截距,得回归方程。20253035404550556065年龄脂肪含量0510152025303540如图 :. 方案2、在图中选两点作直线,使直线两侧 的点的个数基本相同。 20253035404550556065年龄脂肪含量0510152025303540 方案3、如果多取几对点,确定多条直线,再求出这些直线的斜率和截距的平均值作为回归直线的斜率和截距。而得回归方程。 如图: 我们还可以找到
更多的方法,但
这些方法都可行
吗?科学吗?
准确吗?怎样的
方法是最好的?20253035404550556065年龄脂肪含量0510152025303540我们把由一个变量的变化
去推测另一个变量的方法
称为回归方法。我们上面给出的几种方案可靠性都不是很强, 人们经过长期的实践与研究,已经找到了 计算回归方程的斜率与截距的一般公式:通过配方法求得b,再利用回归直线通过样本中心点求得a。它的原理较为简单:即各点到该直线的距离的平方和最小,这一方法叫最小二乘法。回归直线特点:经过样本中心点例1:观察两相关变量得如下表:求两变量间的回归方程解:列表:计算得:小结:求线性回归直线方程的步骤:
第一步:列表 ;
第二步:计算 ;
第三步:代入公式计算b,a的值;
第四步:写出直线方程。课内练习:D(1)设有一个直线回归方程为 ,则变量x 增 加一个单位时( )
A. y 平均增加 1.5 个单位 B. y 平均增加 2 个单位
C. y 平均减少 1.5 个单位 D. y 平均减少 2 个单位C0.50.53课堂练习系列(2)A(2)某产品的广告费支出x(单位:百万元)与销售额y(单位:百万元)之间有如下关系(1)画出散点图,并判断x,y是否线性相关;若线性 相关,求y关于x的回归方程
(2)试预测广告费支出为1000万元时,销售额多大
2、通过收集大量的数据,进行统计,对数据分析,找出其中的规律,对其相关关系作出一定判断. 3、由于变量之间相关关系的广泛性和不确定性,所以样本数据应较大,和有代表性.才能对它们之间的关系作出正确的判断. 从上表发现,对某个人不一定有此规律,但对很多个体放在一起,就体现出“人体脂肪随年龄增长而增加” 这一规律.而表中各年龄对应的脂肪数是这个年龄 人群的样本平均数.我们也可以对它们作统计图、 表,对这两个变量有一个直观上的印象和判断. 下面我们以年龄为横轴,
脂肪含量为纵轴建立直
角坐标系,作出各个点,
称该图为散点图。如图:O20253035404550556065年龄脂肪含量510152025303540我们再观察它的图像发现这些点大致分布在一条直线附 近,像这样,如果散点图中点的分布从整体上看大致在 一条直线附近,我们就称这两个变量之间具有线性相 关关系,这条直线叫做回归直线,该直线叫回归方程。 那么,我们该怎样来求出这个回归方程?
请同学们展开讨论,能得出哪些具体的方案?20253035404550556065年龄脂肪含量0510152025303540. 方案1、先画出一条直线,测量出各点与它的距离,再移动直线,到达一个使距离的和最小时,测出它的斜率和截距,得回归方程。20253035404550556065年龄脂肪含量0510152025303540如图 :. 方案2、在图中选两点作直线,使直线两侧 的点的个数基本相同。 20253035404550556065年龄脂肪含量0510152025303540 方案3、如果多取几对点,确定多条直线,再求出这些直线的斜率和截距的平均值作为回归直线的斜率和截距。而得回归方程。 如图: 我们还可以找到
更多的方法,但
这些方法都可行
吗?科学吗?
准确吗?怎样的
方法是最好的?20253035404550556065年龄脂肪含量0510152025303540我们把由一个变量的变化
去推测另一个变量的方法
称为回归方法。我们上面给出的几种方案可靠性都不是很强, 人们经过长期的实践与研究,已经找到了 计算回归方程的斜率与截距的一般公式:通过配方法求得b,再利用回归直线通过样本中心点求得a。它的原理较为简单:即各点到该直线的距离的平方和最小,这一方法叫最小二乘法。回归直线特点:经过样本中心点例1:观察两相关变量得如下表:求两变量间的回归方程解:列表:计算得:小结:求线性回归直线方程的步骤:
第一步:列表 ;
第二步:计算 ;
第三步:代入公式计算b,a的值;
第四步:写出直线方程。课内练习:D(1)设有一个直线回归方程为 ,则变量x 增 加一个单位时( )
A. y 平均增加 1.5 个单位 B. y 平均增加 2 个单位
C. y 平均减少 1.5 个单位 D. y 平均减少 2 个单位C0.50.53课堂练习系列(2)A(2)某产品的广告费支出x(单位:百万元)与销售额y(单位:百万元)之间有如下关系(1)画出散点图,并判断x,y是否线性相关;若线性 相关,求y关于x的回归方程
(2)试预测广告费支出为1000万元时,销售额多大
