2023年黑龙江省哈尔滨市松北区初中升学调研测试(二)数学试题(含答案)
文档属性
| 名称 | 2023年黑龙江省哈尔滨市松北区初中升学调研测试(二)数学试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 967.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-27 19:15:42 | ||
图片预览



文档简介
松北区2023年初中升学调研测试(二)
数学试卷
考生须知:
1.本试卷满分为120分.考试时间为120分钟;
2.答题前,考生先将自己的“姓名”、“考号”、“考场”、“座位号”在答题卡上填写清楚;
3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效:在草稿纸、试题纸上答题无效;
4.选择题必须使用2B铅笔填涂,非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚;
5.保持卡面整洁,不要折叠、不要弄脏、弄皱,不准使用涂改液、刮纸刀.
第Ⅰ卷 选择题(共30分)涂卡
一、填空题(每小题3分,共30分)
1.的相反数为( )
A. B. C. D.2023
2.下列计算正确的是( )
A. B. C. D.
3.下列图形中,是轴对称但不是中心对称图形的是( )
A. B. C. D.
4.下图所示的几何体是由一些小立方块搭成的,则这个几何体的俯视图是( )
A. B. C. D.
5.将抛物线向左平移1个单位,再向下平移3个单位后所得到的拋物线解析式为( )
A. B. C. D.
6.方程的解为( )
A. B. C. D.
7.如图,已知是低两条切线,为切点.是的直径,若,则的度数为( )
A. B. C. D.
7.某水果园2020年水果产量为40吨,2022年水果产量为60吨,求该果园水果产量的年平均增长率.设该果园水果产量的年平均增长率办,则根据题意可列方程为( )
A. B. C. D.
9.如图,在三角形中,,则的长为( )
A.2 B.5 C.7 D.3
10.某工程队承担了一项修路任务、任务进行一段时间后,提高了工作效率.该工程队修路的长度(单位:)与修路时间(单位:天)之间的函数关系如图所示,则该工程队提高效率前每天修路的长度是( )米.
A.150 B.110 C.75 D.70
第Ⅱ卷 非选择题(共90分)
二、填空题(每小题3分,共30分)
11.将数6530000用科学记数法可表示为____________.
12.在函数中,自变量的取值范围是___________.
13.计算的结果是__________.
14.把多项式分解因式的结果是_____________.
15.不等式组的解集是__________.
16.已知反比例函数的图像经过点,则的值为______.
17.一个扇形的面积为,半径为,则此扇形的圆心角是__________度.
18.分别写有的五张外观形状完全相同的卡片,从中任抽一张,那么抽到表示负数的卡片概率是_________.
19.在正方形外,,点是正方形边上一点,若,则的长为___________.
20.如图,在平行四边形中,,连接,于点,则的长度为_________.
三、解答题(其中21-22题各7分,23-24题各8分,25-27题各10分,共计60分)
21.(本题7分)先化简,再求值:,共中.
22.(本题7分)如图,在每个小正方形的边长均为1的方格纸中,有线段和线段,点均在小正方形的顶点上.
(1)在方格纸中画出以为底的等腰,点在小正方形的顶点上;的面积为;
(2)在方格纸中画出以为一边的等腰,点在小正方形的顶点上,且的面积为5,连接,直接写出的长度.
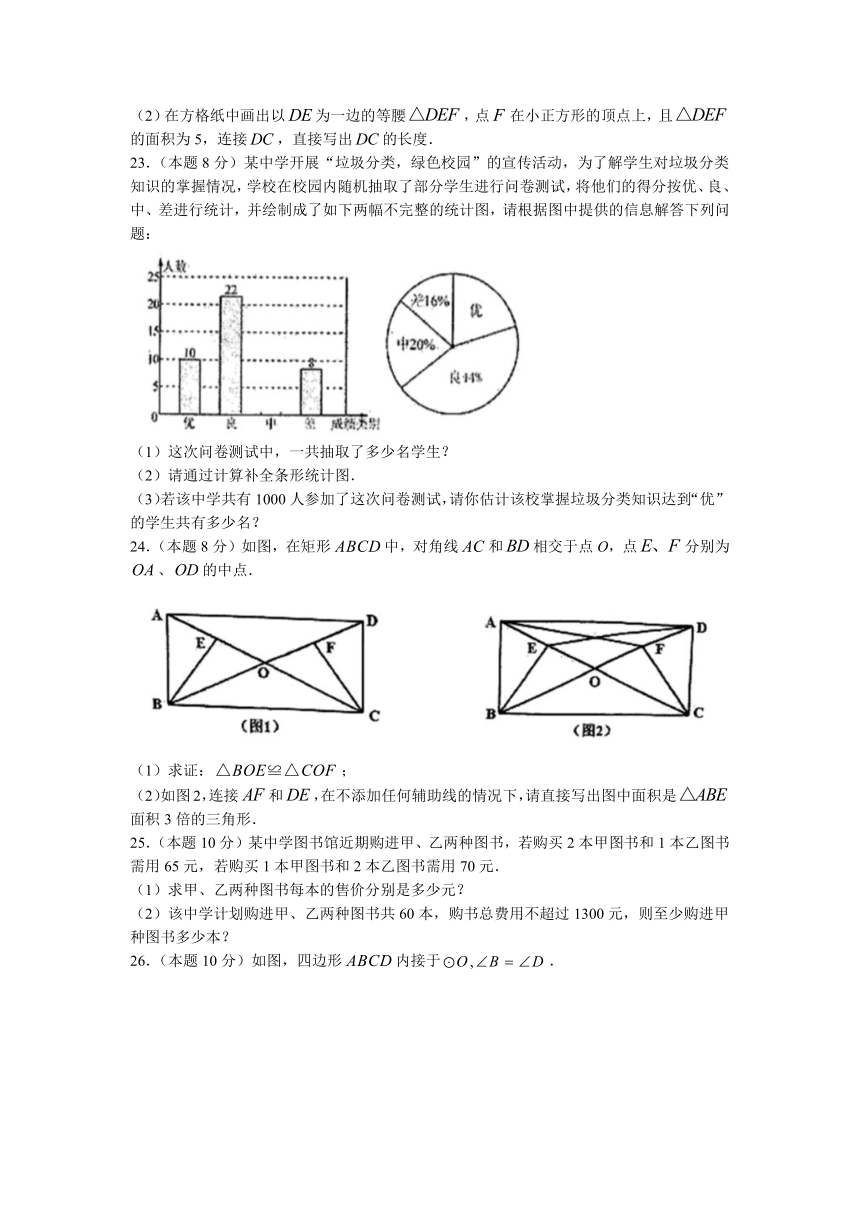
23.(本题8分)某中学开展“垃圾分类,绿色校园”的宣传活动,为了解学生对垃圾分类知识的掌握情况,学校在校园内随机抽取了部分学生进行问卷测试,将他们的得分按优、良、中、差进行统计,并绘制成了如下两幅不完整的统计图,请根据图中提供的信息解答下列问题:
(1)这次问卷测试中,一共抽取了多少名学生?
(2)请通过计算补全条形统计图.
(3)若该中学共有1000人参加了这次问卷测试,请你估计该校掌握垃圾分类知识达到“优”的学生共有多少名?
24.(本题8分)如图,在矩形中,对角线和相交于点O,点分别为、的中点.
(1)求证:;
(2)如图2,连接和,在不添加任何辅助线的情况下,请直接写出图中面积是面积3倍的三角形.
25.(本题10分)某中学图书馆近期购进甲、乙两种图书,若购买2本甲图书和1本乙图书需用65元,若购买1本甲图书和2本乙图书需用70元.
(1)求甲、乙两种图书每本的售价分别是多少元?
(2)该中学计划购进甲、乙两种图书共60本,购书总费用不超过1300元,则至少购进甲种图书多少本?
26.(本题10分)如图,四边形内接于.
(1)求证:;
(2)如图2,在线段上分别取点,连接并延长交于点,连接并延长,交于点,连接,当时,求证:;
(3)在(2)的条件下,当时,若,求的长.
27.(本题10分)如图,抛物线,交轴于点(A左B右),交轴于点,连接,且.
(1)求抛物线的解析式;
(2)点为第三象限拋物线上一点,连接交轴于点,设点的横坐标为,的面积为,求与的函数关系式(不要求写出自变量的取值范围);
(3)在(2)的条件下,过作于点,连接,若,求点的坐标.
答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D C B D A B B A B C
题号 11 12 13 14 15
答案
题号 16 17 18 19 20
答案 4 120 1或 4
21.解:原式
当时
原式
22.(1)如图. (2)如图(满足条件即可给分)
23.解:(1)(名)
答:这次问卷测试中,一共抽取了50名学生.
(2)(人)
正确补图
(3)(名)
答:估计该校掌握垃圾分类知识达到“优”的学生共有200名
(1)证明:
四边形为矩形
点分别为的中点
(2)
(1)解:设甲图书每本售价元,乙图书每本售价元.
答:甲图书每本售价30元,乙图书每本售价15元
(2)解:设购进甲种图书本.
.
答:至少购进甲种图书40本
(1)证明:
四边形为圆的内接四边形
在中,
(2)证明:连接
是的直径
.
(3)解:在上取一点使,在上取一点使,连接.
和是等腰直角三角形.
设为
四边形为矩形
设,
,
在和中,
在中,
为圆的直径,,即
27.(1)抛物线,交轴于点,交轴于点,
当时,
抛物线的解析式为:
(2)点在第三象限抛物线上,
设点的横坐标为,
过点P作轴于点
的面积为
(3)延长交的延长线于点
过C作
且
在中,
数学试卷
考生须知:
1.本试卷满分为120分.考试时间为120分钟;
2.答题前,考生先将自己的“姓名”、“考号”、“考场”、“座位号”在答题卡上填写清楚;
3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效:在草稿纸、试题纸上答题无效;
4.选择题必须使用2B铅笔填涂,非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚;
5.保持卡面整洁,不要折叠、不要弄脏、弄皱,不准使用涂改液、刮纸刀.
第Ⅰ卷 选择题(共30分)涂卡
一、填空题(每小题3分,共30分)
1.的相反数为( )
A. B. C. D.2023
2.下列计算正确的是( )
A. B. C. D.
3.下列图形中,是轴对称但不是中心对称图形的是( )
A. B. C. D.
4.下图所示的几何体是由一些小立方块搭成的,则这个几何体的俯视图是( )
A. B. C. D.
5.将抛物线向左平移1个单位,再向下平移3个单位后所得到的拋物线解析式为( )
A. B. C. D.
6.方程的解为( )
A. B. C. D.
7.如图,已知是低两条切线,为切点.是的直径,若,则的度数为( )
A. B. C. D.
7.某水果园2020年水果产量为40吨,2022年水果产量为60吨,求该果园水果产量的年平均增长率.设该果园水果产量的年平均增长率办,则根据题意可列方程为( )
A. B. C. D.
9.如图,在三角形中,,则的长为( )
A.2 B.5 C.7 D.3
10.某工程队承担了一项修路任务、任务进行一段时间后,提高了工作效率.该工程队修路的长度(单位:)与修路时间(单位:天)之间的函数关系如图所示,则该工程队提高效率前每天修路的长度是( )米.
A.150 B.110 C.75 D.70
第Ⅱ卷 非选择题(共90分)
二、填空题(每小题3分,共30分)
11.将数6530000用科学记数法可表示为____________.
12.在函数中,自变量的取值范围是___________.
13.计算的结果是__________.
14.把多项式分解因式的结果是_____________.
15.不等式组的解集是__________.
16.已知反比例函数的图像经过点,则的值为______.
17.一个扇形的面积为,半径为,则此扇形的圆心角是__________度.
18.分别写有的五张外观形状完全相同的卡片,从中任抽一张,那么抽到表示负数的卡片概率是_________.
19.在正方形外,,点是正方形边上一点,若,则的长为___________.
20.如图,在平行四边形中,,连接,于点,则的长度为_________.
三、解答题(其中21-22题各7分,23-24题各8分,25-27题各10分,共计60分)
21.(本题7分)先化简,再求值:,共中.
22.(本题7分)如图,在每个小正方形的边长均为1的方格纸中,有线段和线段,点均在小正方形的顶点上.
(1)在方格纸中画出以为底的等腰,点在小正方形的顶点上;的面积为;
(2)在方格纸中画出以为一边的等腰,点在小正方形的顶点上,且的面积为5,连接,直接写出的长度.
23.(本题8分)某中学开展“垃圾分类,绿色校园”的宣传活动,为了解学生对垃圾分类知识的掌握情况,学校在校园内随机抽取了部分学生进行问卷测试,将他们的得分按优、良、中、差进行统计,并绘制成了如下两幅不完整的统计图,请根据图中提供的信息解答下列问题:
(1)这次问卷测试中,一共抽取了多少名学生?
(2)请通过计算补全条形统计图.
(3)若该中学共有1000人参加了这次问卷测试,请你估计该校掌握垃圾分类知识达到“优”的学生共有多少名?
24.(本题8分)如图,在矩形中,对角线和相交于点O,点分别为、的中点.
(1)求证:;
(2)如图2,连接和,在不添加任何辅助线的情况下,请直接写出图中面积是面积3倍的三角形.
25.(本题10分)某中学图书馆近期购进甲、乙两种图书,若购买2本甲图书和1本乙图书需用65元,若购买1本甲图书和2本乙图书需用70元.
(1)求甲、乙两种图书每本的售价分别是多少元?
(2)该中学计划购进甲、乙两种图书共60本,购书总费用不超过1300元,则至少购进甲种图书多少本?
26.(本题10分)如图,四边形内接于.
(1)求证:;
(2)如图2,在线段上分别取点,连接并延长交于点,连接并延长,交于点,连接,当时,求证:;
(3)在(2)的条件下,当时,若,求的长.
27.(本题10分)如图,抛物线,交轴于点(A左B右),交轴于点,连接,且.
(1)求抛物线的解析式;
(2)点为第三象限拋物线上一点,连接交轴于点,设点的横坐标为,的面积为,求与的函数关系式(不要求写出自变量的取值范围);
(3)在(2)的条件下,过作于点,连接,若,求点的坐标.
答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D C B D A B B A B C
题号 11 12 13 14 15
答案
题号 16 17 18 19 20
答案 4 120 1或 4
21.解:原式
当时
原式
22.(1)如图. (2)如图(满足条件即可给分)
23.解:(1)(名)
答:这次问卷测试中,一共抽取了50名学生.
(2)(人)
正确补图
(3)(名)
答:估计该校掌握垃圾分类知识达到“优”的学生共有200名
(1)证明:
四边形为矩形
点分别为的中点
(2)
(1)解:设甲图书每本售价元,乙图书每本售价元.
答:甲图书每本售价30元,乙图书每本售价15元
(2)解:设购进甲种图书本.
.
答:至少购进甲种图书40本
(1)证明:
四边形为圆的内接四边形
在中,
(2)证明:连接
是的直径
.
(3)解:在上取一点使,在上取一点使,连接.
和是等腰直角三角形.
设为
四边形为矩形
设,
,
在和中,
在中,
为圆的直径,,即
27.(1)抛物线,交轴于点,交轴于点,
当时,
抛物线的解析式为:
(2)点在第三象限抛物线上,
设点的横坐标为,
过点P作轴于点
的面积为
(3)延长交的延长线于点
过C作
且
在中,
同课章节目录
