圆的切线(复习课)[下学期]
文档属性
| 名称 | 圆的切线(复习课)[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 182.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-10-31 10:53:00 | ||
图片预览


文档简介
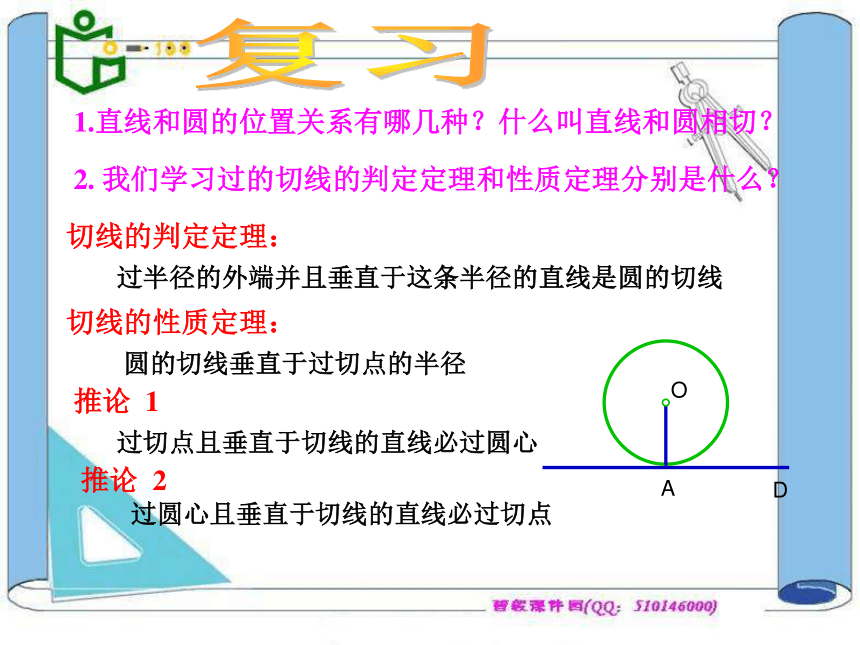
课件14张PPT。长汀二中:曾毅圆的切线(复习课)切线的判定定理:
切线的性质定理:
复习2. 我们学习过的切线的判定定理和性质定理分别是什么?过半径的外端并且垂直于这条半径的直线是圆的切线圆的切线垂直于过切点的半径
推论 1推论 2 过切点且垂直于切线的直线必过圆心过圆心且垂直于切线的直线必过切点1.直线和圆的位置关系有哪几种?什么叫直线和圆相切?
判断对错(1)和圆有公共点的直线是圆的切线。 ( )
(2)经过半径的一个端点并且垂直于这条半径的直线是
圆的切线。 ( )
(3)若一条直线与圆的直径垂直,则这条直线就是圆
的切线。
(4)到圆心的距离等于半径的直线是圆的切线 。 ( )
(5)与两条平行线都相切的圆的直径等于这两条平行线
间的距离。 ( )
(6)与等边三角形的两边相切的圆必定与第三边相切。
( )
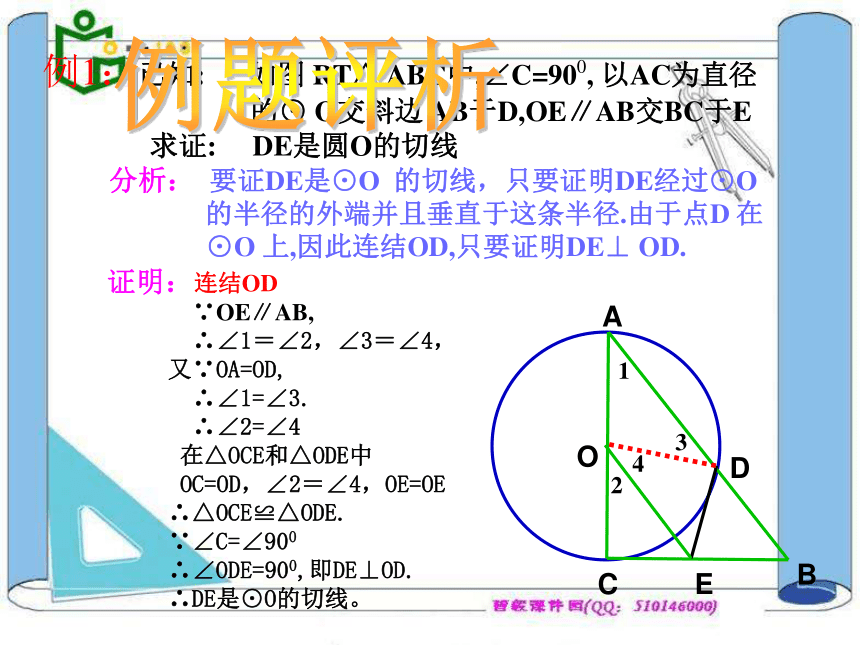
(7)过切点的直径垂直于切线。 ( )× × × × 1234例1:已知: 如图 RT△ ABC中,∠C=900, 以AC为直径
的⊙ O交斜边 AB于D,OE∥AB交BC于E
求证: DE是圆O的切线
?
?
证明:连结OD
∵OE∥AB,
∴∠1=∠2,∠3=∠4,
又∵OA=OD,
∴∠1=∠3.
∴∠2=∠4
在△OCE和△ODE中
OC=OD,∠2=∠4,OE=OE
∴△OCE≌△ODE.
∵∠C=∠900
∴∠ODE=900,即DE⊥OD.
∴DE是⊙O的切线。
分析: 要证DE是⊙O 的切线,只要证明DE经过⊙O
的半径的外端并且垂直于这条半径.由于点D 在
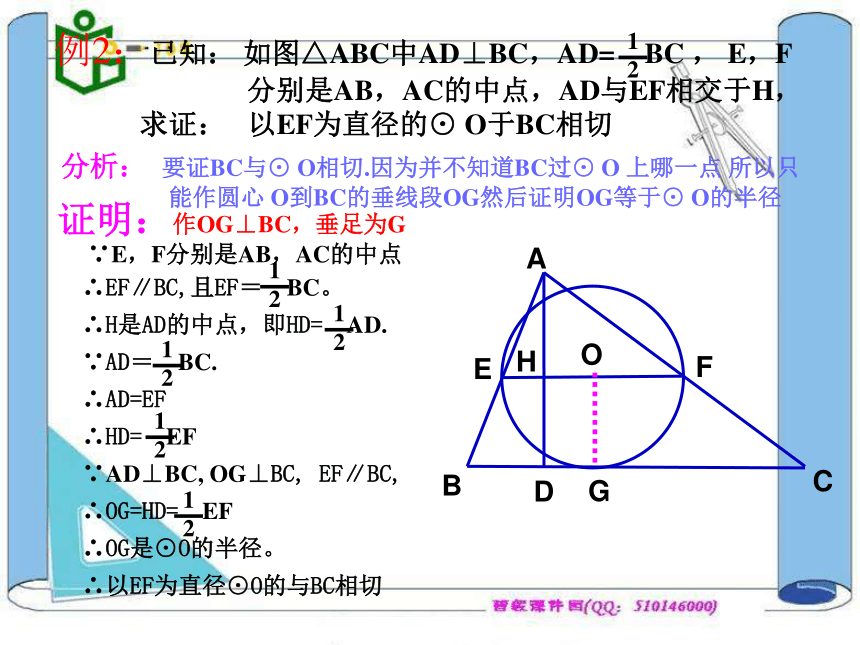
⊙O 上,因此连结OD,只要证明DE⊥ OD.例题评析G分析: 要证BC与⊙ O相切.因为并不知道BC过⊙ O 上哪一点 所以只
能作圆心 O到BC的垂线段OG然后证明OG等于⊙ O的半径
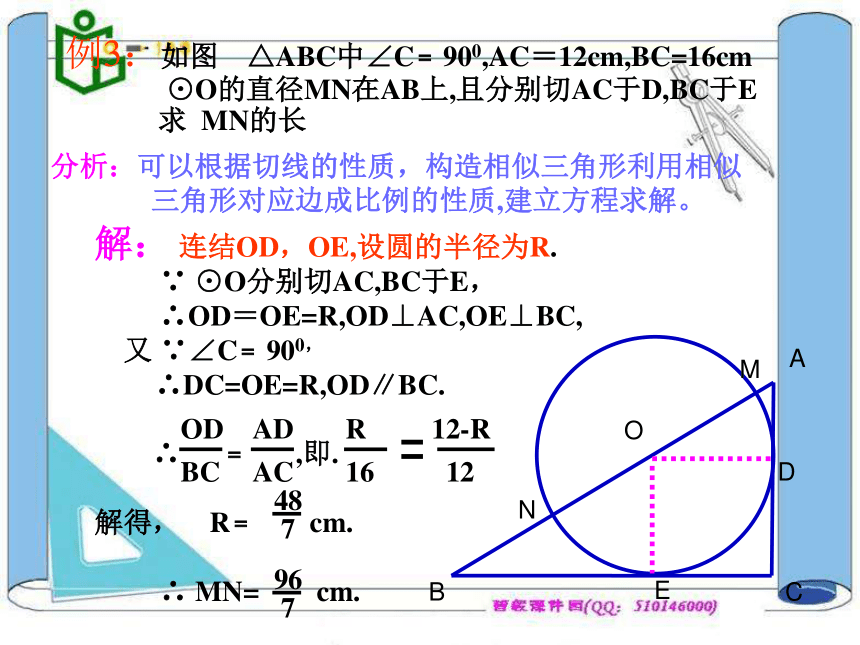
例3:如图 △ABC中∠C﹦900,AC=12cm,BC=16cm
⊙O的直径MN在AB上,且分别切AC于D,BC于E
求 MN的长
分析:可以根据切线的性质,构造相似三角形利用相似
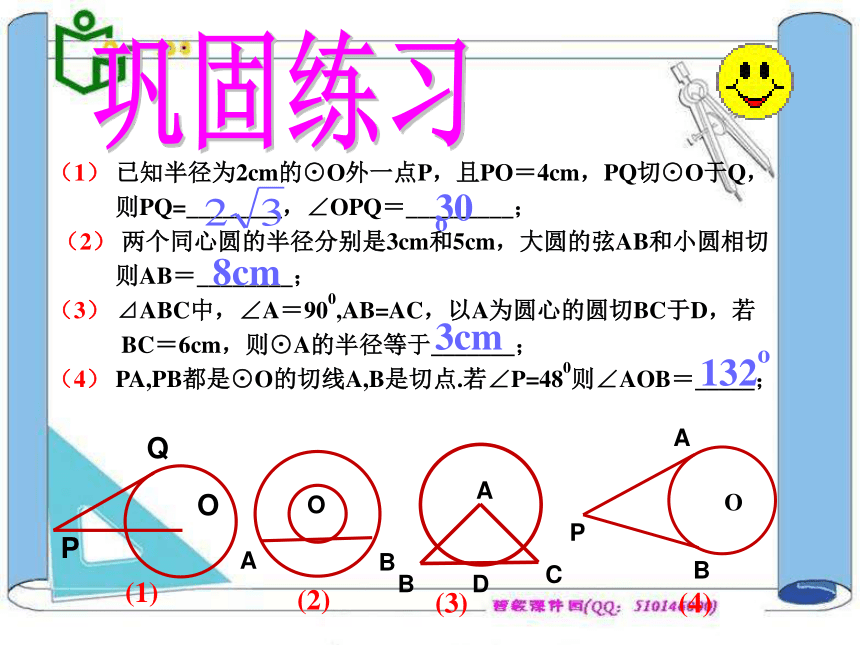
三角形对应边成比例的性质,建立方程求解。巩固练习(1) 已知半径为2cm的⊙O外一点P,且PO=4cm,PQ切⊙O于Q,
则PQ=________,∠OPQ=_________;
?(2) 两个同心圆的半径分别是3cm和5cm,大圆的弦AB和小圆相切
则AB=________;
(3) ⊿ABC中,∠A=900,AB=AC,以A为圆心的圆切BC于D,若
BC=6cm,则⊙A的半径等于_______;
(4) PA,PB都是⊙O的切线A,B是切点.若∠P=480则∠AOB=_____;
30o8cm3cm132o(6) 已知: 如图,⊙O交OA于C,弦BC=AC,∠A=300
求证: AB是⊙C的切线
?? (7) 如图,⊿ABC中,∠C=900,AC=12cm,BC=6cm 点O在
AB上, ⊙O分别切AC,BC于E,F.
求 ⊙O的半径
(5) 已知: 如图,在以O为圆心的两个同心圆中,大圆的弦AB
和CD 相等,且AB与小圆相切于E
求证:CD与小圆相切
?已知 :如图,AB是⊙O的直径,BC是⊙O的切线,切点为B,OC平行于弦AD (1)?求证:DC是⊙O的切线; (2) 若∠DAB=60o,求∠ADC的度数; (3) 若AB长为4,点D在半圆上运动,设AD长为X,点A到直 线CD的距离为Y试求出Y与X之间的函数关系式并求出自变量X 的取值范围; (4) 设⊙O的半径为r,C是切线BE上一动点(点C与B不重合)
试问:当动点C在射线BE上运动到什么位置时有AD= r?请回答并证明你的结论。
1、若AB是⊙O的直径,点C在⊙O上,过C引直径AB的垂线,垂足是D,点D分这条直径成2︰3两部分,如果⊙O的半径等于5,则BC=_____________。 2、已知⊙O的弦CD 直径AB,垂足为P,且AP=3,AB=30,那么CD等于 ( ) A. 9 B. C.18 D. 3、PT切⊙O于T,PAB为经过圆心O的割线,交⊙O于A,B两点,若PT=4,PA=2,则∠BPT的余弦值为 ( ) 4、如图,AE,AD和BC分别切⊙O于E,D,F。如果AD=20,则△ABC的周长为( )
5、如图,⊙O的直径为10,弦AB的长为8,M是弦AB上的动点,则OM的长的取值范围是( ) 6、已知:AB是圆O的直径,C是AB延长线上的一点,CD切圆O于点D,DE⊥AB于点E。
求证: ∠CDB = ∠EDB7、已知:AB是圆O的直径,AC 切圆O于点A,DE切圆O于点E,交AC于点D。
求证:AD=CD 课堂小节
2. 根据切线的性质,构造相似三角形,利用相似三角形对
应边成比例的性质,建立方程求解,是圆的计算中常用
的一种方法。(如例3)
切线的性质定理:
复习2. 我们学习过的切线的判定定理和性质定理分别是什么?过半径的外端并且垂直于这条半径的直线是圆的切线圆的切线垂直于过切点的半径
推论 1推论 2 过切点且垂直于切线的直线必过圆心过圆心且垂直于切线的直线必过切点1.直线和圆的位置关系有哪几种?什么叫直线和圆相切?
判断对错(1)和圆有公共点的直线是圆的切线。 ( )
(2)经过半径的一个端点并且垂直于这条半径的直线是
圆的切线。 ( )
(3)若一条直线与圆的直径垂直,则这条直线就是圆
的切线。
(4)到圆心的距离等于半径的直线是圆的切线 。 ( )
(5)与两条平行线都相切的圆的直径等于这两条平行线
间的距离。 ( )
(6)与等边三角形的两边相切的圆必定与第三边相切。
( )
(7)过切点的直径垂直于切线。 ( )× × × × 1234例1:已知: 如图 RT△ ABC中,∠C=900, 以AC为直径
的⊙ O交斜边 AB于D,OE∥AB交BC于E
求证: DE是圆O的切线
?
?
证明:连结OD
∵OE∥AB,
∴∠1=∠2,∠3=∠4,
又∵OA=OD,
∴∠1=∠3.
∴∠2=∠4
在△OCE和△ODE中
OC=OD,∠2=∠4,OE=OE
∴△OCE≌△ODE.
∵∠C=∠900
∴∠ODE=900,即DE⊥OD.
∴DE是⊙O的切线。
分析: 要证DE是⊙O 的切线,只要证明DE经过⊙O
的半径的外端并且垂直于这条半径.由于点D 在
⊙O 上,因此连结OD,只要证明DE⊥ OD.例题评析G分析: 要证BC与⊙ O相切.因为并不知道BC过⊙ O 上哪一点 所以只
能作圆心 O到BC的垂线段OG然后证明OG等于⊙ O的半径
例3:如图 △ABC中∠C﹦900,AC=12cm,BC=16cm
⊙O的直径MN在AB上,且分别切AC于D,BC于E
求 MN的长
分析:可以根据切线的性质,构造相似三角形利用相似
三角形对应边成比例的性质,建立方程求解。巩固练习(1) 已知半径为2cm的⊙O外一点P,且PO=4cm,PQ切⊙O于Q,
则PQ=________,∠OPQ=_________;
?(2) 两个同心圆的半径分别是3cm和5cm,大圆的弦AB和小圆相切
则AB=________;
(3) ⊿ABC中,∠A=900,AB=AC,以A为圆心的圆切BC于D,若
BC=6cm,则⊙A的半径等于_______;
(4) PA,PB都是⊙O的切线A,B是切点.若∠P=480则∠AOB=_____;
30o8cm3cm132o(6) 已知: 如图,⊙O交OA于C,弦BC=AC,∠A=300
求证: AB是⊙C的切线
?? (7) 如图,⊿ABC中,∠C=900,AC=12cm,BC=6cm 点O在
AB上, ⊙O分别切AC,BC于E,F.
求 ⊙O的半径
(5) 已知: 如图,在以O为圆心的两个同心圆中,大圆的弦AB
和CD 相等,且AB与小圆相切于E
求证:CD与小圆相切
?已知 :如图,AB是⊙O的直径,BC是⊙O的切线,切点为B,OC平行于弦AD (1)?求证:DC是⊙O的切线; (2) 若∠DAB=60o,求∠ADC的度数; (3) 若AB长为4,点D在半圆上运动,设AD长为X,点A到直 线CD的距离为Y试求出Y与X之间的函数关系式并求出自变量X 的取值范围; (4) 设⊙O的半径为r,C是切线BE上一动点(点C与B不重合)
试问:当动点C在射线BE上运动到什么位置时有AD= r?请回答并证明你的结论。
1、若AB是⊙O的直径,点C在⊙O上,过C引直径AB的垂线,垂足是D,点D分这条直径成2︰3两部分,如果⊙O的半径等于5,则BC=_____________。 2、已知⊙O的弦CD 直径AB,垂足为P,且AP=3,AB=30,那么CD等于 ( ) A. 9 B. C.18 D. 3、PT切⊙O于T,PAB为经过圆心O的割线,交⊙O于A,B两点,若PT=4,PA=2,则∠BPT的余弦值为 ( ) 4、如图,AE,AD和BC分别切⊙O于E,D,F。如果AD=20,则△ABC的周长为( )
5、如图,⊙O的直径为10,弦AB的长为8,M是弦AB上的动点,则OM的长的取值范围是( ) 6、已知:AB是圆O的直径,C是AB延长线上的一点,CD切圆O于点D,DE⊥AB于点E。
求证: ∠CDB = ∠EDB7、已知:AB是圆O的直径,AC 切圆O于点A,DE切圆O于点E,交AC于点D。
求证:AD=CD 课堂小节
2. 根据切线的性质,构造相似三角形,利用相似三角形对
应边成比例的性质,建立方程求解,是圆的计算中常用
的一种方法。(如例3)
同课章节目录
