第六章 6.3.5 平面向量数量积的坐标表示(共63张PPT)-高一数学人教A版(2019)必修第二册课件
文档属性
| 名称 | 第六章 6.3.5 平面向量数量积的坐标表示(共63张PPT)-高一数学人教A版(2019)必修第二册课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-28 00:00:00 | ||
图片预览







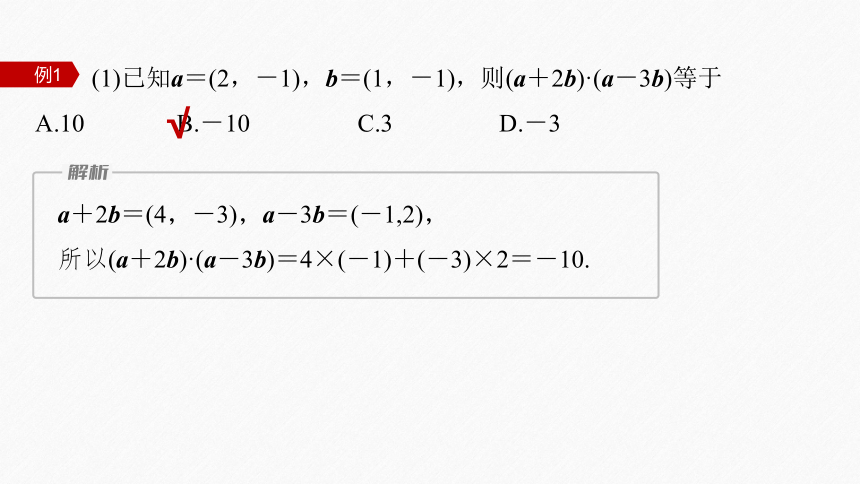




文档简介
(共63张PPT)
6.3.5 平面向量数量积的坐标表示
第六章 §6.3 平面向量基本定理及坐标表示
学习目标
1.掌握平面向量数量积的坐标表示,会进行平面向量数量积的坐标运算.
2.能够用两个向量的坐标来解决与向量的模、夹角、垂直有关的问题.
导语
同学们,前面我们学面向量数量积及其性质,我们也学会了用“坐标语言”去描述向量的加法、减法、数乘运算,那么,我们能否用坐标去表示两向量的数量积呢?
课时对点练
一、平面向量数量积的坐标表示
二、平面向量的模
三、平面向量的夹角、垂直问题
随堂演练
内容索引
平面向量数量积的坐标表示
一
问题 在平面直角坐标系中,设i,j分别是与x轴和y轴方向相同的两个单位向量,你能计算出i·i,j·j,i·j的值吗?若设非零向量a=(x1,y1),b=(x2,y2),你能给出a·b的值吗?
提示 i·i=1,j·j=1,i·j=0.
∵a=x1i+y1j,b=x2i+y2j,
∴a·b=(x1i+y1j)·(x2i+y2j)
=x1x2i2+x1y2i·j+x2y1j·i+y1y2j2.
又∵i·i=1,j·j=1,i·j=j·i=0,
∴a·b=x1x2+y1y2.
设非零向量a=(x1,y1),b=(x2,y2),
则a·b= .这就是说,两个向量的数量积等于它们对应坐标的
.
知识梳理
x1x2+y1y2
乘积的和
(1)已知a=(2,-1),b=(1,-1),则(a+2b)·(a-3b)等于
A.10 B.-10 C.3 D.-3
例1
√
a+2b=(4,-3),a-3b=(-1,2),
所以(a+2b)·(a-3b)=4×(-1)+(-3)×2=-10.
(2)已知a=(1,1),b=(2,5),c=(3,x),若(8a-b)·c=30,则x等于
A.6 B.5 C.4 D.3
√
由题意可得,8a-b=(6,3),
又(8a-b)·c=30,c=(3,x),
∴18+3x=30,解得x=4.
进行向量数量积的坐标运算的注意点
(1)要正确使用公式a·b=x1x2+y1y2,并能灵活运用以下几个关系:
①|a|2=a·a;
②(a+b)·(a-b)=|a|2-|b|2;
③(a+b)2=|a|2+2a·b+|b|2.
(2)在解决平面几何中的数量积的运算时,对于规则的图形,一定要先建立恰当的平面直角坐标系,用向量的坐标法解决平面几何中的数量积的问题.
反思感悟
跟踪训练1
建立平面直角坐标系如图所示,
则A(0,2),E(2,1),D(2,2),B(0,0),C(2,0),
平面向量的模
二
1.若a=(x,y),则|a|2= ,或|a|= .
2.如果表示向量a的有向线段的起点和终点的坐标分别为(x1,y1),(x2,y2),那么a= ,|a|= .
知识梳理
x2+y2
(x2-x1,y2-y1)
例2
√
∵a∥b,∴1×y-2×(-2)=0,
求向量a=(x,y)的模的常见思路及方法
a·a=a2=|a|2或|a|= ,此性质可用来求向量的模,可以实现实数运算与向量运算的相互转化.
反思感悟
跟踪训练2
√
∵a=(2,1),∴a2=5,
即a2+2a·b+b2=50,
∴5+2×10+b2=50,∴b2=25,∴|b|=5.
平面向量的夹角、垂直问题
三
设a,b都是非零向量,a=(x1,y1),b=(x2,y2),θ是a与b的夹角.
知识梳理
(2)a⊥b .
x1x2+y1y2=0
(1)两向量垂直与两向量平行的坐标表示易混淆.
(2)两向量夹角的余弦值大于0的夹角不一定是锐角,同样余弦值小于0的夹角也不一定是钝角.
注意点:
例3
已知a=(4,3),b=(-1,2).
(1)求a与b夹角的余弦值;
因为a·b=4×(-1)+3×2=2,
(2)若(a-λb)⊥(2a+b),求实数λ的值.
因为a-λb=(4+λ,3-2λ),2a+b=(7,8),
又(a-λb)⊥(2a+b),
反思感悟
解决向量夹角问题的方法及注意事项
(2)注意事项:利用三角函数值cos θ求θ的值时,应注意角θ的取值范围是0°≤θ≤180°.利用cos θ= 判断θ的值时,要注意当cos θ<0时,有两种情况:一是θ是钝角,二是θ为180°;当cos θ>0时,也有两种情况:一是θ是锐角,二是θ为0°.
跟踪训练3
因为P(-3,-2),Q(x,2),
(2)已知向量a=(-1,2),b=(m,1).若向量a+b与a垂直,则m=_____.
7
∵a=(-1,2),b=(m,1),
∴a+b=(-1+m,2+1)=(m-1,3).
又a+b与a垂直,
所以(m-1)×(-1)+3×2=0,解得m=7.
课堂
小结
1.知识清单:
(1)平面向量数量积的坐标表示.
(2)平面向量的模.
(3)平面向量的夹角、垂直问题.
2.方法归纳:转化与化归.
3.常见误区:两向量夹角的余弦公式易记错.
随堂演练
1
2
3
4
1.若向量a=(x,2),b=(-1,3),a·b=3,则x等于
√
a·b=-x+6=3,故x=3.
1
2
3
4
√
a·b=3×5+4×12=63.
1
2
3
4
√
由题意2a-b=(3,n),
∵2a-b与b垂直,∴3×(-1)+n2=0,
1
2
3
4
7
课时对点练
1.(多选)设向量a=(2,0),b=(1,1),则下列结论中正确的是
A.|a|=b2 B.a·b=0
C.a∥b D.(a-b)⊥b
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
√
√
|a|=b2=2,故A正确,B,C显然错误;
a-b=(1,-1),所以(a-b)·b=1-1=0,
所以(a-b)⊥b.故D正确.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2.已知向量a=(x,1),b=(1,-2),且a⊥b,则|a+b|等于
由题意可得a·b=x·1+1×(-2)=x-2=0,解得x=2.
再由a+b=(x+1,-1)=(3,-1),
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3.已知A(-2,1),B(6,-3),C(0,5),则△ABC的形状是
A.直角三角形 B.锐角三角形
C.钝角三角形 D.等边三角形
√
所以∠BAC=90°,故△ABC是直角三角形.
4.平面向量a与b的夹角为60°,a=(2,0),|b|=1,则|a+2b|等于
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
a=(2,0),|b|=1,
∴|a|=2,a·b=2×1×cos 60°=1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∵四边形OABC是平行四边形,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
由题意,设b=λa=(λ,-2λ)(λ<0),
又λ<0,∴λ=-3,故b=(-3,6).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
7.已知a=(-1,1),b=(1,2),则a·(a+2b)=_____.
4
∵a+2b=(1,5),∴a·(a+2b)=4.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8.设向量a=(2,3),b=(6,t),若a与b的夹角为锐角,则实数t的取值范围为__________________.
(-4,9)∪(9,+∞)
因为a与b的夹角为锐角,
所以a·b>0,且a与b不共线,
所以实数t的取值范围为(-4,9)∪(9,+∞).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
故c=(-3,3)或c=(3,-3).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
即a2-2a·b=0,所以a·b=1,
(2)若b是单位向量,且a⊥(a-2b),求a与b的夹角θ.
因为θ∈[0,π],
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10.已知向量a=(1, ),b=(-2,0).
(1)求a-b的坐标以及a-b与a的夹角;
设a-b与a的夹角为θ,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
由题意得,|a|=2,|b|=2,a·b=-2,
(2)当t∈[-1,1]时,求|a-tb|的取值范围.
易知当t∈[-1,1]时,|a-tb|2∈[3,12],
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
因为平面向量a与b=(1,-1)方向相同,
所以设a=λ(1,-1)=(λ,-λ)(λ>0),
又因为|a|=2,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
设点P的坐标为(x,0),
=x2-6x+10=(x-3)2+1,
此时点P的坐标为(3,0).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
以A为原点,AB,AD所在直线为x轴、y轴建立如图所示的平面直角坐标系.
∵点E在边CD上,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
拓广探究
15.已知A,B,C是锐角三角形ABC的三个内角,向量p=(sin A,1),q=(1,-cos B),则p与q的夹角是
A.锐角 B.钝角 C.直角 D.不确定
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
因为△ABC是锐角三角形,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
所以p·q=sin A-cos B>0,
又因为p与q不共线,所以p与q的夹角是锐角.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∴x(2-y)-y(-x-4)=0,
即x+2y=0.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
即(x+6)(x-2)+(y+1)(y-3)=0.
由(1)知x+2y=0,与上式联立,
化简得y2-2y-3=0,
解得y=3或y=-1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
当y=3时,x=-6,
本课结束
6.3.5 平面向量数量积的坐标表示
第六章 §6.3 平面向量基本定理及坐标表示
学习目标
1.掌握平面向量数量积的坐标表示,会进行平面向量数量积的坐标运算.
2.能够用两个向量的坐标来解决与向量的模、夹角、垂直有关的问题.
导语
同学们,前面我们学面向量数量积及其性质,我们也学会了用“坐标语言”去描述向量的加法、减法、数乘运算,那么,我们能否用坐标去表示两向量的数量积呢?
课时对点练
一、平面向量数量积的坐标表示
二、平面向量的模
三、平面向量的夹角、垂直问题
随堂演练
内容索引
平面向量数量积的坐标表示
一
问题 在平面直角坐标系中,设i,j分别是与x轴和y轴方向相同的两个单位向量,你能计算出i·i,j·j,i·j的值吗?若设非零向量a=(x1,y1),b=(x2,y2),你能给出a·b的值吗?
提示 i·i=1,j·j=1,i·j=0.
∵a=x1i+y1j,b=x2i+y2j,
∴a·b=(x1i+y1j)·(x2i+y2j)
=x1x2i2+x1y2i·j+x2y1j·i+y1y2j2.
又∵i·i=1,j·j=1,i·j=j·i=0,
∴a·b=x1x2+y1y2.
设非零向量a=(x1,y1),b=(x2,y2),
则a·b= .这就是说,两个向量的数量积等于它们对应坐标的
.
知识梳理
x1x2+y1y2
乘积的和
(1)已知a=(2,-1),b=(1,-1),则(a+2b)·(a-3b)等于
A.10 B.-10 C.3 D.-3
例1
√
a+2b=(4,-3),a-3b=(-1,2),
所以(a+2b)·(a-3b)=4×(-1)+(-3)×2=-10.
(2)已知a=(1,1),b=(2,5),c=(3,x),若(8a-b)·c=30,则x等于
A.6 B.5 C.4 D.3
√
由题意可得,8a-b=(6,3),
又(8a-b)·c=30,c=(3,x),
∴18+3x=30,解得x=4.
进行向量数量积的坐标运算的注意点
(1)要正确使用公式a·b=x1x2+y1y2,并能灵活运用以下几个关系:
①|a|2=a·a;
②(a+b)·(a-b)=|a|2-|b|2;
③(a+b)2=|a|2+2a·b+|b|2.
(2)在解决平面几何中的数量积的运算时,对于规则的图形,一定要先建立恰当的平面直角坐标系,用向量的坐标法解决平面几何中的数量积的问题.
反思感悟
跟踪训练1
建立平面直角坐标系如图所示,
则A(0,2),E(2,1),D(2,2),B(0,0),C(2,0),
平面向量的模
二
1.若a=(x,y),则|a|2= ,或|a|= .
2.如果表示向量a的有向线段的起点和终点的坐标分别为(x1,y1),(x2,y2),那么a= ,|a|= .
知识梳理
x2+y2
(x2-x1,y2-y1)
例2
√
∵a∥b,∴1×y-2×(-2)=0,
求向量a=(x,y)的模的常见思路及方法
a·a=a2=|a|2或|a|= ,此性质可用来求向量的模,可以实现实数运算与向量运算的相互转化.
反思感悟
跟踪训练2
√
∵a=(2,1),∴a2=5,
即a2+2a·b+b2=50,
∴5+2×10+b2=50,∴b2=25,∴|b|=5.
平面向量的夹角、垂直问题
三
设a,b都是非零向量,a=(x1,y1),b=(x2,y2),θ是a与b的夹角.
知识梳理
(2)a⊥b .
x1x2+y1y2=0
(1)两向量垂直与两向量平行的坐标表示易混淆.
(2)两向量夹角的余弦值大于0的夹角不一定是锐角,同样余弦值小于0的夹角也不一定是钝角.
注意点:
例3
已知a=(4,3),b=(-1,2).
(1)求a与b夹角的余弦值;
因为a·b=4×(-1)+3×2=2,
(2)若(a-λb)⊥(2a+b),求实数λ的值.
因为a-λb=(4+λ,3-2λ),2a+b=(7,8),
又(a-λb)⊥(2a+b),
反思感悟
解决向量夹角问题的方法及注意事项
(2)注意事项:利用三角函数值cos θ求θ的值时,应注意角θ的取值范围是0°≤θ≤180°.利用cos θ= 判断θ的值时,要注意当cos θ<0时,有两种情况:一是θ是钝角,二是θ为180°;当cos θ>0时,也有两种情况:一是θ是锐角,二是θ为0°.
跟踪训练3
因为P(-3,-2),Q(x,2),
(2)已知向量a=(-1,2),b=(m,1).若向量a+b与a垂直,则m=_____.
7
∵a=(-1,2),b=(m,1),
∴a+b=(-1+m,2+1)=(m-1,3).
又a+b与a垂直,
所以(m-1)×(-1)+3×2=0,解得m=7.
课堂
小结
1.知识清单:
(1)平面向量数量积的坐标表示.
(2)平面向量的模.
(3)平面向量的夹角、垂直问题.
2.方法归纳:转化与化归.
3.常见误区:两向量夹角的余弦公式易记错.
随堂演练
1
2
3
4
1.若向量a=(x,2),b=(-1,3),a·b=3,则x等于
√
a·b=-x+6=3,故x=3.
1
2
3
4
√
a·b=3×5+4×12=63.
1
2
3
4
√
由题意2a-b=(3,n),
∵2a-b与b垂直,∴3×(-1)+n2=0,
1
2
3
4
7
课时对点练
1.(多选)设向量a=(2,0),b=(1,1),则下列结论中正确的是
A.|a|=b2 B.a·b=0
C.a∥b D.(a-b)⊥b
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
√
√
|a|=b2=2,故A正确,B,C显然错误;
a-b=(1,-1),所以(a-b)·b=1-1=0,
所以(a-b)⊥b.故D正确.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2.已知向量a=(x,1),b=(1,-2),且a⊥b,则|a+b|等于
由题意可得a·b=x·1+1×(-2)=x-2=0,解得x=2.
再由a+b=(x+1,-1)=(3,-1),
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3.已知A(-2,1),B(6,-3),C(0,5),则△ABC的形状是
A.直角三角形 B.锐角三角形
C.钝角三角形 D.等边三角形
√
所以∠BAC=90°,故△ABC是直角三角形.
4.平面向量a与b的夹角为60°,a=(2,0),|b|=1,则|a+2b|等于
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
a=(2,0),|b|=1,
∴|a|=2,a·b=2×1×cos 60°=1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∵四边形OABC是平行四边形,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
由题意,设b=λa=(λ,-2λ)(λ<0),
又λ<0,∴λ=-3,故b=(-3,6).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
7.已知a=(-1,1),b=(1,2),则a·(a+2b)=_____.
4
∵a+2b=(1,5),∴a·(a+2b)=4.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8.设向量a=(2,3),b=(6,t),若a与b的夹角为锐角,则实数t的取值范围为__________________.
(-4,9)∪(9,+∞)
因为a与b的夹角为锐角,
所以a·b>0,且a与b不共线,
所以实数t的取值范围为(-4,9)∪(9,+∞).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
故c=(-3,3)或c=(3,-3).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
即a2-2a·b=0,所以a·b=1,
(2)若b是单位向量,且a⊥(a-2b),求a与b的夹角θ.
因为θ∈[0,π],
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10.已知向量a=(1, ),b=(-2,0).
(1)求a-b的坐标以及a-b与a的夹角;
设a-b与a的夹角为θ,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
由题意得,|a|=2,|b|=2,a·b=-2,
(2)当t∈[-1,1]时,求|a-tb|的取值范围.
易知当t∈[-1,1]时,|a-tb|2∈[3,12],
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
因为平面向量a与b=(1,-1)方向相同,
所以设a=λ(1,-1)=(λ,-λ)(λ>0),
又因为|a|=2,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
设点P的坐标为(x,0),
=x2-6x+10=(x-3)2+1,
此时点P的坐标为(3,0).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
以A为原点,AB,AD所在直线为x轴、y轴建立如图所示的平面直角坐标系.
∵点E在边CD上,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
拓广探究
15.已知A,B,C是锐角三角形ABC的三个内角,向量p=(sin A,1),q=(1,-cos B),则p与q的夹角是
A.锐角 B.钝角 C.直角 D.不确定
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
因为△ABC是锐角三角形,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
所以p·q=sin A-cos B>0,
又因为p与q不共线,所以p与q的夹角是锐角.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∴x(2-y)-y(-x-4)=0,
即x+2y=0.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
即(x+6)(x-2)+(y+1)(y-3)=0.
由(1)知x+2y=0,与上式联立,
化简得y2-2y-3=0,
解得y=3或y=-1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
当y=3时,x=-6,
本课结束
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
