第八章 成对数据的统计分析 单元测试-2022-2023学年高二下学期数学人教A版(2019)选择性必修第三册(含答案)
文档属性
| 名称 | 第八章 成对数据的统计分析 单元测试-2022-2023学年高二下学期数学人教A版(2019)选择性必修第三册(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 475.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-28 00:00:00 | ||
图片预览




文档简介
2022——2023学年第二学期高中数学选择性必修三
第八章成对数据的统计分析单元测试
一、单选题
1.某市物价部门对5家商场的某商品一天的销售量及其价格进行调查,5家商场的售价(元)和销售量(件)之间的一组数据如表所示:
价格 9 9.5 10 10.5 11
销售量 11 10 8 6 5
按公式计算,与的回归直线方程是:,相关系数,则下列说法错误的是( )
A.变量,线性负相关且相关性较强; B.;
C.当时,的估计值为12.8; D.相应于点的残差为0.4.
2.过,,三点的回归直线方程是( )
A. B. C. D.
3.春节期间,“履行节约,反对浪费”之风悄然吹开,某市通过随机询问100名性别不同的居民能否做到“光盘”得到如下的列联表:
单位:人
不能做到“光盘” 能做到“光盘” 合计
男 45 10 55
女 30 15 45
合计 75 25 100
附:
0.1 0.05 0.01 0.005 0.001
2.706 3.841 6.635 7.879 10.828
,其中.
参照附表,得到的正确结论是( )
A.在犯错误的概率不超过0.01的前提下认为“该市居民能否做到‘光盘’与性别有关”
B.在犯错误的概率不超过0.01的前提下认为“该市居民能否做到‘光盘’与性别无关”
C.在犯错误的概率不超过0.1的前提下认为“该市居民能否做到‘光盘’与性别有关”
D.在犯错误的概率不超过0.1的前提下认为“该市居民能否做到‘光盘’与性别无关”
4.2020年初,新型冠状病毒()引起的肺炎疫情爆发以来,各地医疗机构采取了各种针对性的治疗方法,取得了不错的成效某地开始使用中西医结合方法后,每周治愈的患者人数如下表所示:
周数() 1 2 3 4 5
治愈人数() 2 17 36 103 142
由表格可得关于的回归方程为,则此回归模型第4周的残差(实际值与预报值之差)为( ).
A.5 B. C.13 D.0
5.为了研究某班学生的脚长(单位:厘米)和身高(单位:厘米)的关系,从该班随机抽取10名学生,根据测量数据的散点图可以看出与之间有线性相关关系,设其回归直线方程为,已知,,,已知该班某学生的脚长为24厘米,据此估计其身高为( )厘米.
A.165 B.169 C.173 D.178
6.已知,的取值如下表所示:
x 0 1 3 4
y 2.2 4.3 4.8 6.7
若与线性相关,且,则( )
A.2.2 B.2.9 C.2.8 D.2.6
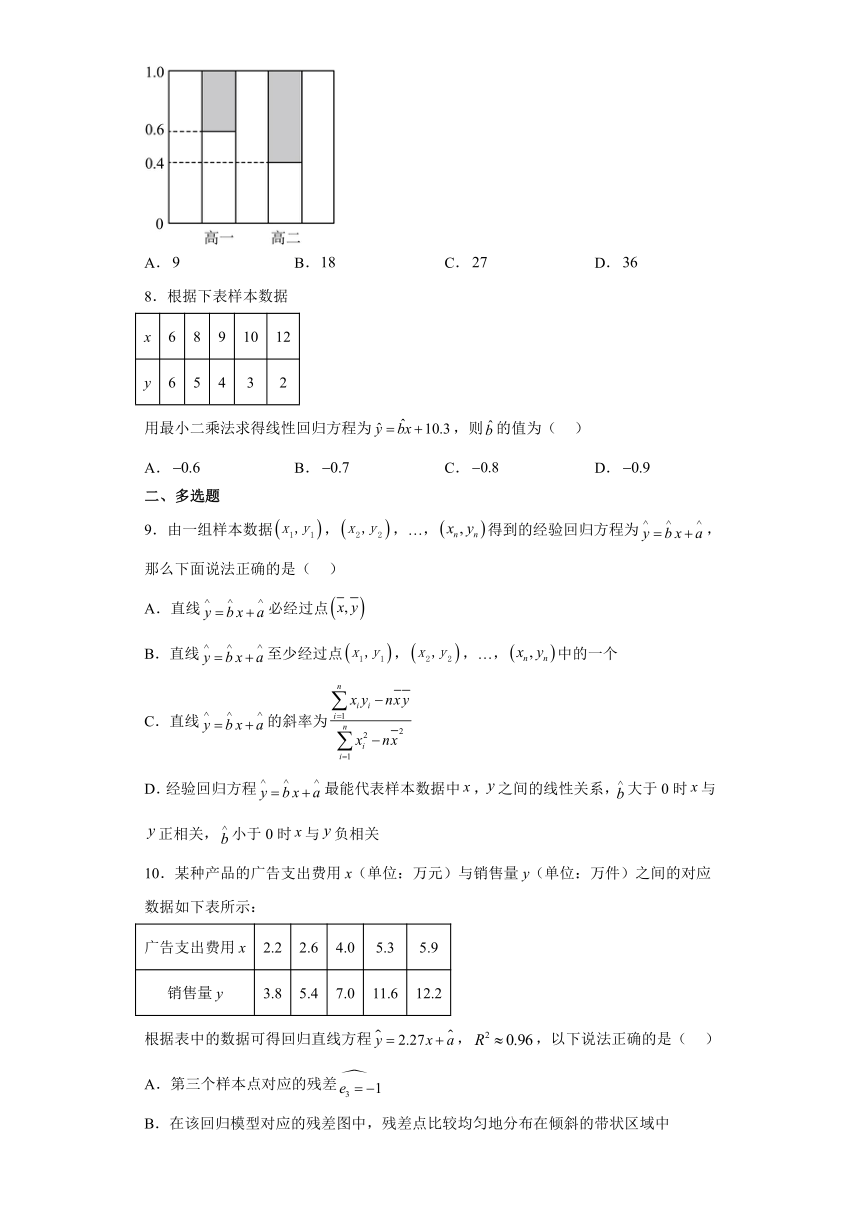
7.如图是调查某学校高一、高二年级学生参加社团活动的等高条形图,阴影部分的高表示参加社团的频率.已知该校高一、高二年级学生人数均为人(所有学生都参加了调查),现从参加社团的同学中按分层抽样的方式抽取人,则抽取的高二学生人数为( )
A. B. C. D.
8.根据下表样本数据
x 6 8 9 10 12
y 6 5 4 3 2
用最小二乘法求得线性回归方程为,则的值为( )
A. B. C. D.
二、多选题
9.由一组样本数据,,…,得到的经验回归方程为,那么下面说法正确的是( )
A.直线必经过点
B.直线至少经过点,,…,中的一个
C.直线的斜率为
D.经验回归方程最能代表样本数据中,之间的线性关系,大于0时与正相关,小于0时与负相关
10.某种产品的广告支出费用x(单位:万元)与销售量y(单位:万件)之间的对应数据如下表所示:
广告支出费用x 2.2 2.6 4.0 5.3 5.9
销售量y 3.8 5.4 7.0 11.6 12.2
根据表中的数据可得回归直线方程,,以下说法正确的是( )
A.第三个样本点对应的残差
B.在该回归模型对应的残差图中,残差点比较均匀地分布在倾斜的带状区域中
C.销售量的多少有是由广告支出费用引起的
D.用该回归方程可以比较准确地预测广告费用为20万元时的销售量
11.已知由样本数据点集合,求得的回归直线方程为,且,现发现两个数据点和误差较大,去除后重新求得的回归直线l的斜率为1.2,则( )
A.变量x与y具有正相关关系 B.去除后的回归方程为
C.去除后y的估计值增加速度变快 D.去除后相应于样本点的残差为0.05
12.某中学为了解性别因素是否对本校学生体育锻炼的经常性有影响,从本校所有学生中随机调查了50名男生和50名女生,得到如下列联表:
经常锻炼 不经常锻炼
男 40 10
女 30 20
a 0.1 0.05 0.01
2.706 3.841 6.635
经计算,则可以推断出( )
A.该学校男生中经常体育锻炼的概率的估计值为
B.该学校男生比女生更经常锻炼
C.有95%的把握认为男、女生在体育锻炼的经常性方面有差异
D.有99%的把握认为男、女生在体育锻炼的经常性方面有差异
三、填空题
13.某医疗研究所为了检验某种血清预防感冒的作用,把名使用血清的人与另外名未使用血清的人一年中的感冒记录作比较,提出假设:“这种血清不能起到预防感冒的作用”,利用列联表计算得,经查临界值表知.则下列结论中,正确结论的序号是________.
①在犯错误的概率不超过的前提下认为“这种血清能起到预防感冒的作用”;
②若某人未使用该血清,那么他在一年中有的可能性得感冒;
③这种血清预防感冒的有效率为;
④这种血清预防感冒的有效率为.
14.给出下列说法:
①回归直线恒过样本点的中心;
②某7个数的平均数为4,方差为2,现加入一个新数据4,此时这8个数的方差不变;
③在回归直线方程中,当变量x增加一个单位时,平均减少0.5个单位.
其中说法正确的是_____________.
15.有如下四个命题:
①甲乙两组数据分别甲:1,2,3,4,5,6,7,8,9;乙:1,2,3,4,5,6,7,8,9,10.则甲乙的中位数分别为5和5.5.
②相关系数,表明两个变量的相关性较弱.
③若由一个列联表中的数据计算得的观测值约为4.567,则认为两个变量有关,此推断犯错误的概率不超过0.05.
附
0.050 0.010 0.001
3.841 6.635 10.828
④用最小二乘法求出一组数据的回归直线方程后要进行残差分析,相应数据的残差是指.
以上命题错误的序号是__________.
16.某中学共有学生5000名,其中男生3500名,女生1500名,为了解该校学生每周平均体育锻炼时间的情况以及该校学生每周平均体育锻炼时间是否与性别有关,现用分层随机抽样的方法从中收集300名学生每周平均体育锻炼时间的样本数据(单位:),其频率分布直方图如下:
已知在样本数据中,有60名女生的每周平均体育锻炼时间不少于4h,根据独立性检验原理,我们有______的把握认为该校学生每周平均体育锻炼时间与性别有关.
四、解答题
17.近年来,“双11”网购的观念逐渐深入人心.某人统计了近年某网站“双11”当天的交易额,统计结果如下表:
年份 2015 2016 2017 2018 2019
年份代码x 1 2 3 4 5
交易额y/百亿元 9 12 17 21 26
(1)请根据上表提供的数据,用相关系数说明与的线性相关程度,线性相关系数保留三位小数.(统计中用相关系数来衡量两个变量之间线性关系的强弱.若相应于变量的取值,变量的观测值为(),则两个变量的相关系数的计算公式为:.统计学认为,对于变量,如果,那么负相关很强;如果,那么正相关很强;如果或,那么相关性一般;如果,那么相关性较弱);
(2)求出关于的线性回归方程,并预测年该网站“双11”当天的交易额.
参考公式:,;参考数据:.
18.为加强素质教育,提升学生综合素养,某中学为高一年级提供了“书法”和“剪纸”两门选修课.为了了解选择“书法”或“剪纸”是否与性别有关,调查了高一年级1500名学生的选择倾向,随机抽取了100人,统计选择两门课程人数如下表:
(1)补全2×2列联表;
选书法 选剪纸 共计
男生 40 50
女生
共计 30
(2)是否有的把握认为选择“书法”或“剪纸”与性别有关?(计算结果保留到小数点后三位,例如:3.841)
参考附表:
0.100 0.050 0.025
2.706 3.841 5.024
参考公式:,其中.
19.为打造“四态融合、产村一体”,望山、见水、忆乡愁的美丽乡村,增加农民收入,某乡政府统计了景区农家乐在年年中任选年的接待游客人数(单位:万人)的数据,结果如下表:
年份
年份代号
接待游客人数(单位:万人)
(1)求相关系数的值,并说明年份与接待游客人数之间线性关系的强弱;(值精确到)
(2)求关于的线性回归方程.(系数用分数表示)
附:线性回归方程的斜率及截距的最小二乘法估计分别为,,相关系数,一般地,当的绝对值大于时,认为两个变量之间有较强的线性相关程度.
参考数据:,,,,.
20.近年来,师范专业是高考考生填报志愿的热门专业.某高中随机调查了本校2022年参加高考的90位考生首选志愿(第一个院校专业组的第一个专业)填报情况,经统计,首选志愿填报与性别情况如下表:(单位:人)
首选志愿为师范专业 首选志愿为非师范专业
女性 25 35
男性 5 25
(1)根据表中数据并依据小概率值α=0.05的独立性检验,分析首选志愿为师范专业与性别是否有关联.
(2)用样本估计总体,用本次调研中首选志愿样本的频率代替首选志愿的概率,从2022年全国考生中随机抽取3人,设被抽取的3人中首选志愿为师范专业的人数为,求的分布列、数学期望和方差.
附:,.
0.15 0.10 0.05 0.025 0.010 0.005 0.001
2.072 2.706 3.841 5.024 6.635 7.879 10.828
21.皮影戏是一种民间艺术,是我国民间工艺美术与戏曲巧妙结合而成的独特艺术品种,已有千余年的历史.而皮影制作是一项复杂的制作技艺,要求制作者必须具备扎实的绘画功底和高超的雕刻技巧,以及持之以恒的毅力和韧劲.每次制作分为画图与剪裁,雕刻与着色,刷清与装备三道主要工序,经过以上工序处理之后,一幅幅形态各异,富有神韵的皮影在能工巧匠的手里浑然天成,成为可供人们欣赏和操纵的富有灵气的影人.小李对学习皮影制作产生极大兴趣,师从名师勒学苦练,目前水平突飞猛进,三道主要工序中每道工序制作合格的概率依次为,三道序彼此独立,只有当每道工序制作都合格才为一次成功的皮影制作,该皮影视为合格作品.
(1)求小李进行3次皮影制作,恰有一次合格作品的概率;
(2)若小李制作15次,其中合格作品数为X,求X的数学期望与方差;
(3)随着制作技术的不断提高,小李制作的皮影作品被某皮影戏剧团看中,聘其为单位制作演出作品,决定试用一段时间,每天制作皮影作品,其中前7天制作合格作品数y与时间:如下表:(第1天用数字1表示)
时间(t) 1 2 3 4 5 6 7
合格作品数(y) 3 4 3 4 7 6 8
其中合格作品数(y)与时间(t)具有线性相关关系,求y关于t的线性回归方程(精确到0.01),并估算第15天能制作多少个合格作品(四舍五入取整)?
(参考公式,,参考数据:).
22.为了研究一种新药治疗某种疾病是否有效,进行了临床试验.采用有放回简单随机抽样的方法得到如下数据:抽到服用新药的患者55名,其中45名治愈,10名未治愈;抽到服用安慰剂(没有任何疗效)的患者45名,其中25名治愈,20名未治愈.
(1)根据上述信息完成服用新药和治疗该种疾病的样本数据的列联表;
疗法 疗效 合计
治愈 未治愈
服用新药
服用安慰剂
合计
(2)依据的独立性检验,能否认为新药对治疗该种疾病有效?并解释得到的结论.
附:;
0.10 0.01 0.001
2.706 6.635 10.828
答案:
1.D 2.C 3.C 4.C 5.B 6.D 7.C 8.B
9.ACD 10.AC 11.AB 12.BC
13.① 14.①③ 15.② 16.95%
17.(1)由题意,根据表格中的数据,
可得:,,
则,
,
所以,
所以变量与的线性相关程度很强.
(2)由(1)可得,,,
又由,
所以,则,
可得关于的线性回归方程为,
令,可得,
即年该网站“双11”当天的交易额百亿元.
18.(1)根据题意补全2×2列联表,如下:
选书法 选剪纸 共计
男生 40 10 50
女生 30 20 50
共计 70 30 100
(2)根据列联表中数据,得,
所以有的把握认为选“书法”或“剪纸”与性别有关.
19.(1)由题中数据可得,,
,
,
又,,
.
由于,故年份与接待游客人数之间有较强的线性相关程度.
(2)由已知及(1)可得,,
,
关于的线性回归方程为.
20.(1),
∴依据小概率值α=0.05的独立性检验,认为首选志愿为师范专业与性别有关联.
(2)某个考生首选志愿为师范专业的概率,
的所有可能取值为0,1,2,3,
,,
,,
∴的分布列如下:
0 1 2 3
∴,.
或由的二项分布知,.
21.(1)小李制作一次皮影合格的概率,
小李进行3次制作,恰有一次合格作品的概率.
(2)由题知:,则.
(3).
,,,,
,,
所以回归直线方程为.当时,,
所以第15天能制作14个合格作品.
22.(1)解:由题意可得新药和该种疾病的样本数据的列联表如下:
疗法 疗效 合计
治愈 未治愈
服用新药 45 10 55
服用安慰剂 25 20 45
合计 70 30 100
(2)解:零假设:假设新药对治疗该种疾病无效,
根据列联表中的数据,可得,
根据小概率值的独立性检验,推断出不成立,即认为新药对该种疾病治疗,此推断犯错误的概率不超过,
服用新药中治愈和未治愈的频率分别为和,服用安慰剂治愈和未治愈的频率分别为和,
根据频率稳定于概率的原理,可认为服用新药治愈该疾病的概率大;
第八章成对数据的统计分析单元测试
一、单选题
1.某市物价部门对5家商场的某商品一天的销售量及其价格进行调查,5家商场的售价(元)和销售量(件)之间的一组数据如表所示:
价格 9 9.5 10 10.5 11
销售量 11 10 8 6 5
按公式计算,与的回归直线方程是:,相关系数,则下列说法错误的是( )
A.变量,线性负相关且相关性较强; B.;
C.当时,的估计值为12.8; D.相应于点的残差为0.4.
2.过,,三点的回归直线方程是( )
A. B. C. D.
3.春节期间,“履行节约,反对浪费”之风悄然吹开,某市通过随机询问100名性别不同的居民能否做到“光盘”得到如下的列联表:
单位:人
不能做到“光盘” 能做到“光盘” 合计
男 45 10 55
女 30 15 45
合计 75 25 100
附:
0.1 0.05 0.01 0.005 0.001
2.706 3.841 6.635 7.879 10.828
,其中.
参照附表,得到的正确结论是( )
A.在犯错误的概率不超过0.01的前提下认为“该市居民能否做到‘光盘’与性别有关”
B.在犯错误的概率不超过0.01的前提下认为“该市居民能否做到‘光盘’与性别无关”
C.在犯错误的概率不超过0.1的前提下认为“该市居民能否做到‘光盘’与性别有关”
D.在犯错误的概率不超过0.1的前提下认为“该市居民能否做到‘光盘’与性别无关”
4.2020年初,新型冠状病毒()引起的肺炎疫情爆发以来,各地医疗机构采取了各种针对性的治疗方法,取得了不错的成效某地开始使用中西医结合方法后,每周治愈的患者人数如下表所示:
周数() 1 2 3 4 5
治愈人数() 2 17 36 103 142
由表格可得关于的回归方程为,则此回归模型第4周的残差(实际值与预报值之差)为( ).
A.5 B. C.13 D.0
5.为了研究某班学生的脚长(单位:厘米)和身高(单位:厘米)的关系,从该班随机抽取10名学生,根据测量数据的散点图可以看出与之间有线性相关关系,设其回归直线方程为,已知,,,已知该班某学生的脚长为24厘米,据此估计其身高为( )厘米.
A.165 B.169 C.173 D.178
6.已知,的取值如下表所示:
x 0 1 3 4
y 2.2 4.3 4.8 6.7
若与线性相关,且,则( )
A.2.2 B.2.9 C.2.8 D.2.6
7.如图是调查某学校高一、高二年级学生参加社团活动的等高条形图,阴影部分的高表示参加社团的频率.已知该校高一、高二年级学生人数均为人(所有学生都参加了调查),现从参加社团的同学中按分层抽样的方式抽取人,则抽取的高二学生人数为( )
A. B. C. D.
8.根据下表样本数据
x 6 8 9 10 12
y 6 5 4 3 2
用最小二乘法求得线性回归方程为,则的值为( )
A. B. C. D.
二、多选题
9.由一组样本数据,,…,得到的经验回归方程为,那么下面说法正确的是( )
A.直线必经过点
B.直线至少经过点,,…,中的一个
C.直线的斜率为
D.经验回归方程最能代表样本数据中,之间的线性关系,大于0时与正相关,小于0时与负相关
10.某种产品的广告支出费用x(单位:万元)与销售量y(单位:万件)之间的对应数据如下表所示:
广告支出费用x 2.2 2.6 4.0 5.3 5.9
销售量y 3.8 5.4 7.0 11.6 12.2
根据表中的数据可得回归直线方程,,以下说法正确的是( )
A.第三个样本点对应的残差
B.在该回归模型对应的残差图中,残差点比较均匀地分布在倾斜的带状区域中
C.销售量的多少有是由广告支出费用引起的
D.用该回归方程可以比较准确地预测广告费用为20万元时的销售量
11.已知由样本数据点集合,求得的回归直线方程为,且,现发现两个数据点和误差较大,去除后重新求得的回归直线l的斜率为1.2,则( )
A.变量x与y具有正相关关系 B.去除后的回归方程为
C.去除后y的估计值增加速度变快 D.去除后相应于样本点的残差为0.05
12.某中学为了解性别因素是否对本校学生体育锻炼的经常性有影响,从本校所有学生中随机调查了50名男生和50名女生,得到如下列联表:
经常锻炼 不经常锻炼
男 40 10
女 30 20
a 0.1 0.05 0.01
2.706 3.841 6.635
经计算,则可以推断出( )
A.该学校男生中经常体育锻炼的概率的估计值为
B.该学校男生比女生更经常锻炼
C.有95%的把握认为男、女生在体育锻炼的经常性方面有差异
D.有99%的把握认为男、女生在体育锻炼的经常性方面有差异
三、填空题
13.某医疗研究所为了检验某种血清预防感冒的作用,把名使用血清的人与另外名未使用血清的人一年中的感冒记录作比较,提出假设:“这种血清不能起到预防感冒的作用”,利用列联表计算得,经查临界值表知.则下列结论中,正确结论的序号是________.
①在犯错误的概率不超过的前提下认为“这种血清能起到预防感冒的作用”;
②若某人未使用该血清,那么他在一年中有的可能性得感冒;
③这种血清预防感冒的有效率为;
④这种血清预防感冒的有效率为.
14.给出下列说法:
①回归直线恒过样本点的中心;
②某7个数的平均数为4,方差为2,现加入一个新数据4,此时这8个数的方差不变;
③在回归直线方程中,当变量x增加一个单位时,平均减少0.5个单位.
其中说法正确的是_____________.
15.有如下四个命题:
①甲乙两组数据分别甲:1,2,3,4,5,6,7,8,9;乙:1,2,3,4,5,6,7,8,9,10.则甲乙的中位数分别为5和5.5.
②相关系数,表明两个变量的相关性较弱.
③若由一个列联表中的数据计算得的观测值约为4.567,则认为两个变量有关,此推断犯错误的概率不超过0.05.
附
0.050 0.010 0.001
3.841 6.635 10.828
④用最小二乘法求出一组数据的回归直线方程后要进行残差分析,相应数据的残差是指.
以上命题错误的序号是__________.
16.某中学共有学生5000名,其中男生3500名,女生1500名,为了解该校学生每周平均体育锻炼时间的情况以及该校学生每周平均体育锻炼时间是否与性别有关,现用分层随机抽样的方法从中收集300名学生每周平均体育锻炼时间的样本数据(单位:),其频率分布直方图如下:
已知在样本数据中,有60名女生的每周平均体育锻炼时间不少于4h,根据独立性检验原理,我们有______的把握认为该校学生每周平均体育锻炼时间与性别有关.
四、解答题
17.近年来,“双11”网购的观念逐渐深入人心.某人统计了近年某网站“双11”当天的交易额,统计结果如下表:
年份 2015 2016 2017 2018 2019
年份代码x 1 2 3 4 5
交易额y/百亿元 9 12 17 21 26
(1)请根据上表提供的数据,用相关系数说明与的线性相关程度,线性相关系数保留三位小数.(统计中用相关系数来衡量两个变量之间线性关系的强弱.若相应于变量的取值,变量的观测值为(),则两个变量的相关系数的计算公式为:.统计学认为,对于变量,如果,那么负相关很强;如果,那么正相关很强;如果或,那么相关性一般;如果,那么相关性较弱);
(2)求出关于的线性回归方程,并预测年该网站“双11”当天的交易额.
参考公式:,;参考数据:.
18.为加强素质教育,提升学生综合素养,某中学为高一年级提供了“书法”和“剪纸”两门选修课.为了了解选择“书法”或“剪纸”是否与性别有关,调查了高一年级1500名学生的选择倾向,随机抽取了100人,统计选择两门课程人数如下表:
(1)补全2×2列联表;
选书法 选剪纸 共计
男生 40 50
女生
共计 30
(2)是否有的把握认为选择“书法”或“剪纸”与性别有关?(计算结果保留到小数点后三位,例如:3.841)
参考附表:
0.100 0.050 0.025
2.706 3.841 5.024
参考公式:,其中.
19.为打造“四态融合、产村一体”,望山、见水、忆乡愁的美丽乡村,增加农民收入,某乡政府统计了景区农家乐在年年中任选年的接待游客人数(单位:万人)的数据,结果如下表:
年份
年份代号
接待游客人数(单位:万人)
(1)求相关系数的值,并说明年份与接待游客人数之间线性关系的强弱;(值精确到)
(2)求关于的线性回归方程.(系数用分数表示)
附:线性回归方程的斜率及截距的最小二乘法估计分别为,,相关系数,一般地,当的绝对值大于时,认为两个变量之间有较强的线性相关程度.
参考数据:,,,,.
20.近年来,师范专业是高考考生填报志愿的热门专业.某高中随机调查了本校2022年参加高考的90位考生首选志愿(第一个院校专业组的第一个专业)填报情况,经统计,首选志愿填报与性别情况如下表:(单位:人)
首选志愿为师范专业 首选志愿为非师范专业
女性 25 35
男性 5 25
(1)根据表中数据并依据小概率值α=0.05的独立性检验,分析首选志愿为师范专业与性别是否有关联.
(2)用样本估计总体,用本次调研中首选志愿样本的频率代替首选志愿的概率,从2022年全国考生中随机抽取3人,设被抽取的3人中首选志愿为师范专业的人数为,求的分布列、数学期望和方差.
附:,.
0.15 0.10 0.05 0.025 0.010 0.005 0.001
2.072 2.706 3.841 5.024 6.635 7.879 10.828
21.皮影戏是一种民间艺术,是我国民间工艺美术与戏曲巧妙结合而成的独特艺术品种,已有千余年的历史.而皮影制作是一项复杂的制作技艺,要求制作者必须具备扎实的绘画功底和高超的雕刻技巧,以及持之以恒的毅力和韧劲.每次制作分为画图与剪裁,雕刻与着色,刷清与装备三道主要工序,经过以上工序处理之后,一幅幅形态各异,富有神韵的皮影在能工巧匠的手里浑然天成,成为可供人们欣赏和操纵的富有灵气的影人.小李对学习皮影制作产生极大兴趣,师从名师勒学苦练,目前水平突飞猛进,三道主要工序中每道工序制作合格的概率依次为,三道序彼此独立,只有当每道工序制作都合格才为一次成功的皮影制作,该皮影视为合格作品.
(1)求小李进行3次皮影制作,恰有一次合格作品的概率;
(2)若小李制作15次,其中合格作品数为X,求X的数学期望与方差;
(3)随着制作技术的不断提高,小李制作的皮影作品被某皮影戏剧团看中,聘其为单位制作演出作品,决定试用一段时间,每天制作皮影作品,其中前7天制作合格作品数y与时间:如下表:(第1天用数字1表示)
时间(t) 1 2 3 4 5 6 7
合格作品数(y) 3 4 3 4 7 6 8
其中合格作品数(y)与时间(t)具有线性相关关系,求y关于t的线性回归方程(精确到0.01),并估算第15天能制作多少个合格作品(四舍五入取整)?
(参考公式,,参考数据:).
22.为了研究一种新药治疗某种疾病是否有效,进行了临床试验.采用有放回简单随机抽样的方法得到如下数据:抽到服用新药的患者55名,其中45名治愈,10名未治愈;抽到服用安慰剂(没有任何疗效)的患者45名,其中25名治愈,20名未治愈.
(1)根据上述信息完成服用新药和治疗该种疾病的样本数据的列联表;
疗法 疗效 合计
治愈 未治愈
服用新药
服用安慰剂
合计
(2)依据的独立性检验,能否认为新药对治疗该种疾病有效?并解释得到的结论.
附:;
0.10 0.01 0.001
2.706 6.635 10.828
答案:
1.D 2.C 3.C 4.C 5.B 6.D 7.C 8.B
9.ACD 10.AC 11.AB 12.BC
13.① 14.①③ 15.② 16.95%
17.(1)由题意,根据表格中的数据,
可得:,,
则,
,
所以,
所以变量与的线性相关程度很强.
(2)由(1)可得,,,
又由,
所以,则,
可得关于的线性回归方程为,
令,可得,
即年该网站“双11”当天的交易额百亿元.
18.(1)根据题意补全2×2列联表,如下:
选书法 选剪纸 共计
男生 40 10 50
女生 30 20 50
共计 70 30 100
(2)根据列联表中数据,得,
所以有的把握认为选“书法”或“剪纸”与性别有关.
19.(1)由题中数据可得,,
,
,
又,,
.
由于,故年份与接待游客人数之间有较强的线性相关程度.
(2)由已知及(1)可得,,
,
关于的线性回归方程为.
20.(1),
∴依据小概率值α=0.05的独立性检验,认为首选志愿为师范专业与性别有关联.
(2)某个考生首选志愿为师范专业的概率,
的所有可能取值为0,1,2,3,
,,
,,
∴的分布列如下:
0 1 2 3
∴,.
或由的二项分布知,.
21.(1)小李制作一次皮影合格的概率,
小李进行3次制作,恰有一次合格作品的概率.
(2)由题知:,则.
(3).
,,,,
,,
所以回归直线方程为.当时,,
所以第15天能制作14个合格作品.
22.(1)解:由题意可得新药和该种疾病的样本数据的列联表如下:
疗法 疗效 合计
治愈 未治愈
服用新药 45 10 55
服用安慰剂 25 20 45
合计 70 30 100
(2)解:零假设:假设新药对治疗该种疾病无效,
根据列联表中的数据,可得,
根据小概率值的独立性检验,推断出不成立,即认为新药对该种疾病治疗,此推断犯错误的概率不超过,
服用新药中治愈和未治愈的频率分别为和,服用安慰剂治愈和未治愈的频率分别为和,
根据频率稳定于概率的原理,可认为服用新药治愈该疾病的概率大;
