沪科版九年级数学下册试题 24.2 圆的基本性质 一课一练 (含答案)
文档属性
| 名称 | 沪科版九年级数学下册试题 24.2 圆的基本性质 一课一练 (含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 168.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-29 16:24:40 | ||
图片预览



文档简介
24.2 圆的基本性质
一、选择题
1.如图,△ABC是⊙O的内接三角形,半径OB=3,sinA=,则弦BC的长为( )
A.3 B.4 C.5 D.3.75
2.矩形ABCD中,AB=5,BC=12,如果分别以A、C为圆心的两圆外切,且点D在圆C内,点B在圆C外,那么圆A的半径r的取值范围是( )
A.5<r<12 B.18<r<25 C.1<r<8 D.5<r<8
3.如图,⊙O内切于正方形ABCD,O为圆心,作∠MON=90°,其两边分别交BC,CD于点N,M,若CM+CN=4,则⊙O的面积为( )
A.π B.2π C.4π D.0.5π
4.如图,△ABC内接于⊙O,AC=5,BC=12,且∠A=90°+∠B,则点O到AB的距离为( )
A. B. C. D.4
5.如图,OA是⊙O的半径,B为OA上一点(且不与点O、A重合),过点B作OA的垂线交⊙O于点C.以OB、BC为边作矩形OBCD,连结BD.若BD=10,BC=8,则AB的长为( )
A.8 B.6 C.4 D.2
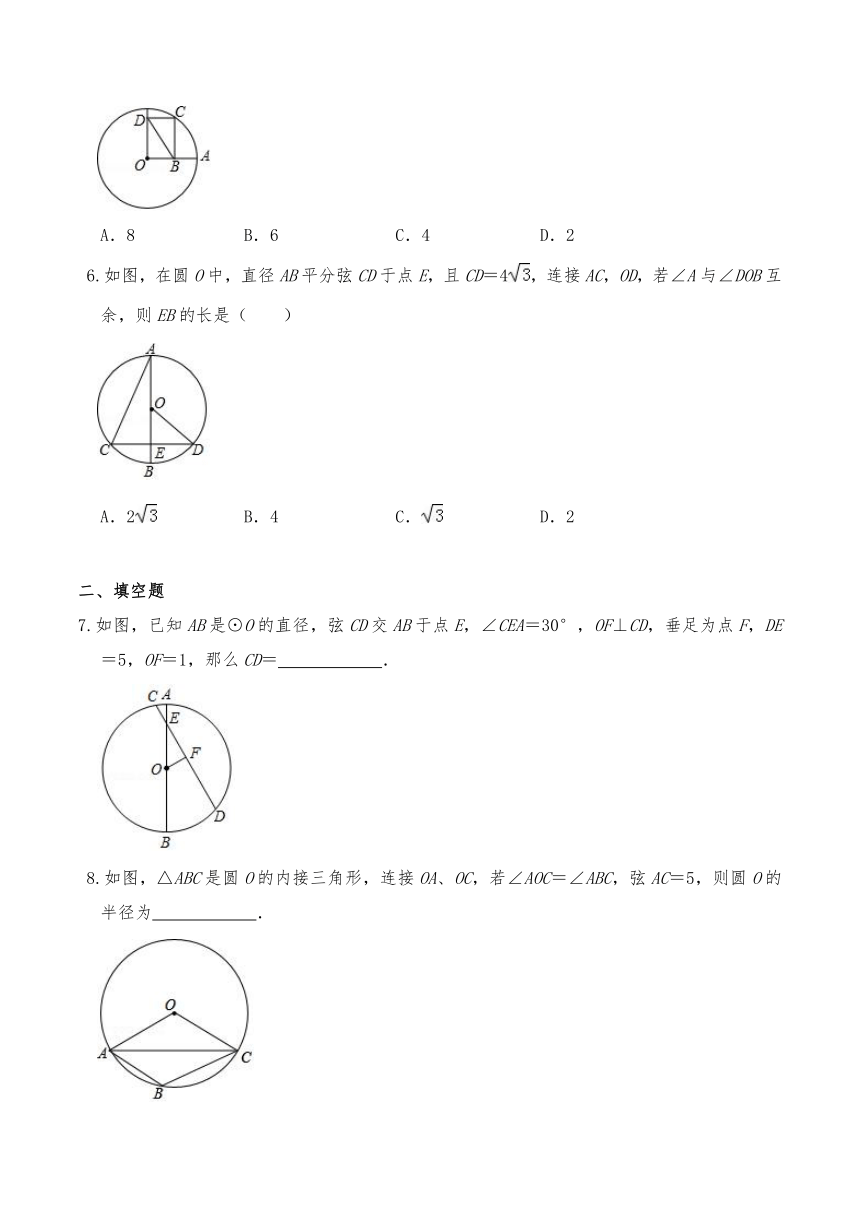
6.如图,在圆O中,直径AB平分弦CD于点E,且CD=4,连接AC,OD,若∠A与∠DOB互余,则EB的长是( )
A.2 B.4 C. D.2
二、填空题
7.如图,已知AB是⊙O的直径,弦CD交AB于点E,∠CEA=30°,OF⊥CD,垂足为点F,DE=5,OF=1,那么CD= .
8.如图,△ABC是圆O的内接三角形,连接OA、OC,若∠AOC=∠ABC,弦AC=5,则圆O的半径为 .
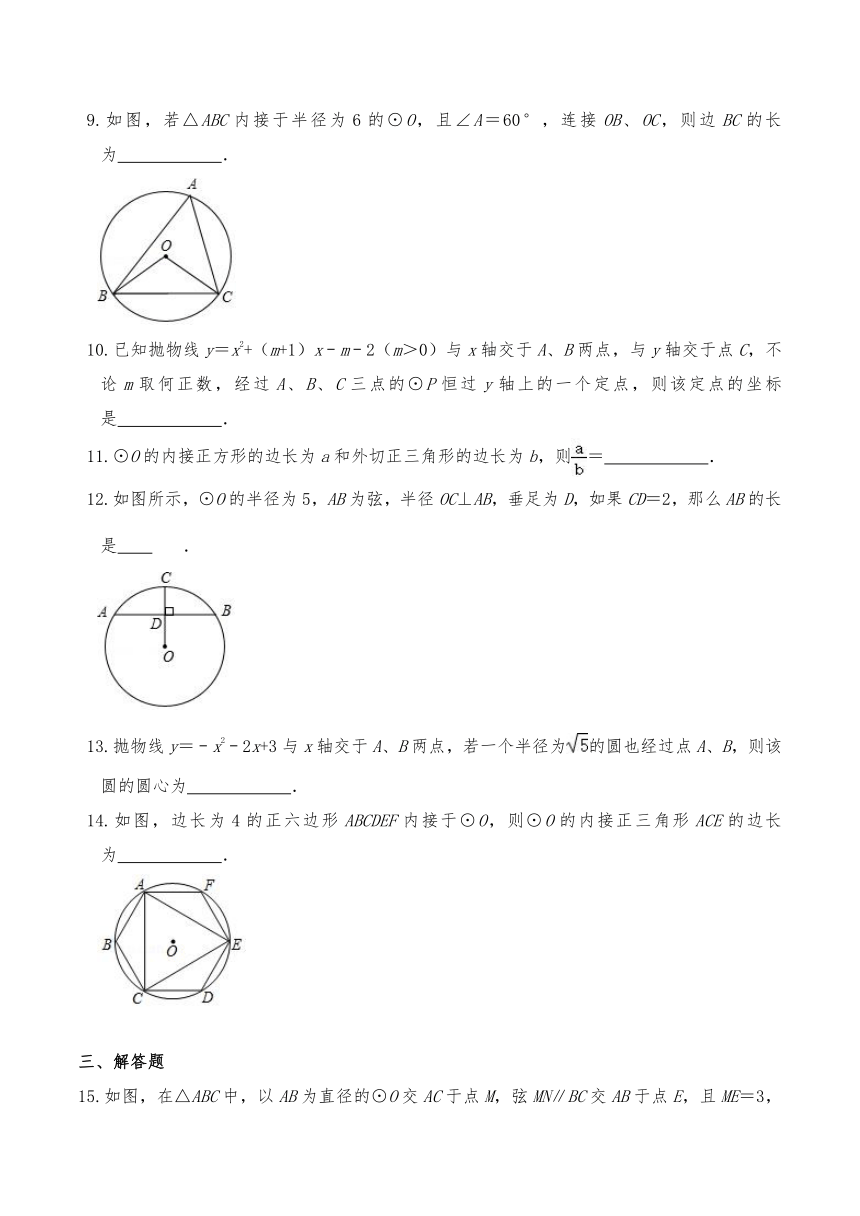
9.如图,若△ABC内接于半径为6的⊙O,且∠A=60°,连接OB、OC,则边BC的长为 .
10.已知抛物线y=x2+(m+1)x﹣m﹣2(m>0)与x轴交于A、B两点,与y轴交于点C,不论m取何正数,经过A、B、C三点的⊙P恒过y轴上的一个定点,则该定点的坐标是 .
11.⊙O的内接正方形的边长为a和外切正三角形的边长为b,则= .
12.如图所示,⊙O的半径为5,AB为弦,半径OC⊥AB,垂足为D,如果CD=2,那么AB的长是 .
13.抛物线y=﹣x2﹣2x+3与x轴交于A、B两点,若一个半径为的圆也经过点A、B,则该圆的圆心为 .
14.如图,边长为4的正六边形ABCDEF内接于⊙O,则⊙O的内接正三角形ACE的边长为 .
三、解答题
15.如图,在△ABC中,以AB为直径的⊙O交AC于点M,弦MN∥BC交AB于点E,且ME=3,AE=4,AM=5.
(1)求证:BC是⊙O的切线;
(2)求⊙O的直径AB的长度.
16.如图,有一拱桥的桥拱是圆弧形,已知桥拱的水面跨度AB(弧所对的弦的长)为8米,拱高CD(弧的中点到弦的距离)为2米.
(1)求桥拱所在圆的半径长;
(2)如果水面AB上升到EF时,从点E测得桥顶D的仰角为α,且cotα=3,求水面上升的高度.
17.如图,在Rt△ABC中,∠ABC=90°,AB=CB,以AB为直径的⊙O交AC于点D,点E是AB边上一点(点E不与点A,B重合),DE的延长线交⊙O于点G,DF⊥DG,且交BC于点F.
(1)求证:AE=BF.
(2)连接GB,EF,求证:GB∥EF.
(3)若AE=2,EB=4,求DG的长.
18.已知:如图,四边形ABCD内接于⊙O,AC和BD相交于E,BC=CD=4,AE=6,且BE和DE的长是正整数,求BD的长.
19.如图:△ABC是⊙O的内接三角形,∠ACB=45°,∠AOC=150°,过点C作⊙O的切线交AB的延长线于点D.
(1)求证:CD=CB;
(2)如果⊙O的半径为2,求AC的长.
20.如图已知⊙O经过A、B两点,AB=6,C是的中点,联结OC交弦AB与点D,CD=1.
(1)求圆⊙O的半径;
(2)过点B、点O分别作点AO、AB的平行线,交于点G,E是⊙O上一点,联结EG交⊙O于点F,当EF=AB,求sin∠OGE的值.
答案
一、选择题
B.C.C.B.C.D.
二、填空题
7.10﹣2.
8..
9.6.
10.(0,1).
11..
12.8.
13.(﹣1,1)或(﹣1,﹣1).
14.4.
三、解答题
15.(1)证明:∵在△AME中,ME=3,AE=4,AM=5,
∴AM2=ME2+AE2,
∴△AME是直角三角形,
∴∠AEM=90°,
又∵MN∥BC,
∴∠ABC=∠AEM=90°,
∴AB⊥BC,
∵AB为直径,
∴BC是⊙O的切线;
(2)解:连接OM,如图,设⊙O的半径是r,
在Rt△OEM中,OE=AE﹣OA=4﹣r,ME=3,OM=r,
∵OM2=ME2+OE2,
∴r2=32+(4﹣r)2,
解得:r=,
∴AB=2r=.
16.解:(1)∵,DC⊥AB,
∴AC=BC,DC经过圆心,
设拱桥的桥拱弧AB所在圆的圆心为O,
∵AB=8,
∴AC=BC=4,
联结OA,设半径OA=OD=R,OC=OD﹣DC=R﹣2,
∵OD⊥AB,
∴∠ACO=90°,
在Rt△ACO中,∵OA2=AC2+OC2,
∴R2=(R﹣2)2+42,
解之得R=5.
答:桥拱所在圆的半径长为5米.
(2)设OD与EF相交于点G,联结OE,
∵EF∥AB,OD⊥AB,
∴OD⊥EF,
∴∠EGD=∠EGO=90°,
在Rt△EGD中,,
∴EG=3DG,
设水面上升的高度为x米,即CG=x,则DG=2﹣x,
∴EG=6﹣3x,
在Rt△EGO中,∵EG2+OG2=OE2,
∴(6﹣3x)2+(3+x)2=52,
化简得 x2﹣3x+2=0,解得 x1=2(舍去),x2=1,
答:水面上升的高度为1米.
17.(1)证明:连接BD.如图,
在Rt△ABC中,∠ABC=90°,AB=BC,
∴∠A=∠C=45°.
∵AB是⊙O的直径,
∴∠ADB=90°,即BD⊥AC,
∴BD=AD=CD,∠CBD=∠C=45°,
∵DF⊥DG,∠FDG=90°,
∴∠FDB+∠BDG=90°,
又∵∠EDA+∠BDG=90°,
∴∠EDA=∠FDB,
在△AED和△BFD中,
∴△AED≌△BFD(ASA),
∴AE=BF;
(2)证明:如图,由(1)知△AED≌△BFD,
∴DE=DF.
∵∠EDF=90°.
∴△EDF是等腰直角三角形,
∴∠DEF=45°,
∵∠G=∠A=45°.
∴∠G=∠DEF,
∴GB∥EF;
(3)解:∵AE=BF,AE=2,
∴BF=2.
在Rt△EBF中,EF==2,
∵△DED为等腰直角三角形,∠EDF=90°,
∴DE=EF=×2=,
∵∠G=∠A,∠GEB=∠AED,
∴△GEB∽△AED,
∴,即GE DE=AE BE,
∴GE==,
∴DG=GE+ED=+=.
18.解:∵BC=CD=4,
∴,
∴∠CBE=∠CDB=∠CAB,
又∵∠BCE=∠ACB,
∴△CBE∽△CAB,
∴=,即=,
整理得:EC2+6EC﹣16=0,
解得:EC=2,或EC=﹣8(舍去),
∴EC=2,
由相交弦定理得:BE×ED=AE×EC,
∴BE×ED=2×6=12,
∵BE和DE的长是正整数,
∴BE和DE的取值分别为3,4或2,6或1,12;
∵BC=CD=4,
∴BD<BC+CD=4+4=8,
∴BD=3+4=7.
19.(1)证明:连接OB,则∠AOB=2∠ACB=2×45°=90°,
∵OA=OB,
∴∠OAB=OBA=45°,
∵∠AOC=150°,OA=OC,
∴∠OCA=∠OAC=15°,
∴∠OCB=∠OCA+∠ACB=60°,
∴△OBC是等边三角形,
∴∠BOC=∠OBC=60°,
∴∠CBD=180°﹣∠OBA﹣∠OBC=75°,
∵CD是⊙O的切线,
∴OC⊥CD,
∴∠D=360°﹣∠OBD﹣∠BOC﹣∠OCD=360°﹣(60°+75°)﹣60°﹣90°=75°,
∴∠CBD=∠D,
∴CB=CD;
(2)在Rt△AOB中,AB=OA=2,
∵CD是⊙O的切线,
∴∠DCB=∠CAD,
∵∠D是公共角,
∴△DBC∽△DCA,
∴=
∴CD2=AD BD=BD (BD+AB),
∵CD=BC=OC=2,
∴4=BD (2+BD),
解得:BD=﹣,
∴AC=AD=AB+BD=+.
20.解:(1)∵AB=6,C是的中点,CD=1,
∴OC⊥AB且OC平分AB,
∴AD=3,∠ODA=90°,
设OA=r,则OD=r﹣1,
∴r2=32+(r﹣1)2,
解得,r=5,
即圆⊙O的半径为5;
(2)作OH⊥EF于点H,
∵AB=EF,OD=r﹣1=4,
∴OH=OD=4,∠OHG=90°,
∵OA∥BG,OG∥AB,
∴四边形OABG是平行四边形,
∴OG=AB,
∵AB=6,
∴OG=6,
∴sin∠OGH===,
即sin∠OGE=.
一、选择题
1.如图,△ABC是⊙O的内接三角形,半径OB=3,sinA=,则弦BC的长为( )
A.3 B.4 C.5 D.3.75
2.矩形ABCD中,AB=5,BC=12,如果分别以A、C为圆心的两圆外切,且点D在圆C内,点B在圆C外,那么圆A的半径r的取值范围是( )
A.5<r<12 B.18<r<25 C.1<r<8 D.5<r<8
3.如图,⊙O内切于正方形ABCD,O为圆心,作∠MON=90°,其两边分别交BC,CD于点N,M,若CM+CN=4,则⊙O的面积为( )
A.π B.2π C.4π D.0.5π
4.如图,△ABC内接于⊙O,AC=5,BC=12,且∠A=90°+∠B,则点O到AB的距离为( )
A. B. C. D.4
5.如图,OA是⊙O的半径,B为OA上一点(且不与点O、A重合),过点B作OA的垂线交⊙O于点C.以OB、BC为边作矩形OBCD,连结BD.若BD=10,BC=8,则AB的长为( )
A.8 B.6 C.4 D.2
6.如图,在圆O中,直径AB平分弦CD于点E,且CD=4,连接AC,OD,若∠A与∠DOB互余,则EB的长是( )
A.2 B.4 C. D.2
二、填空题
7.如图,已知AB是⊙O的直径,弦CD交AB于点E,∠CEA=30°,OF⊥CD,垂足为点F,DE=5,OF=1,那么CD= .
8.如图,△ABC是圆O的内接三角形,连接OA、OC,若∠AOC=∠ABC,弦AC=5,则圆O的半径为 .
9.如图,若△ABC内接于半径为6的⊙O,且∠A=60°,连接OB、OC,则边BC的长为 .
10.已知抛物线y=x2+(m+1)x﹣m﹣2(m>0)与x轴交于A、B两点,与y轴交于点C,不论m取何正数,经过A、B、C三点的⊙P恒过y轴上的一个定点,则该定点的坐标是 .
11.⊙O的内接正方形的边长为a和外切正三角形的边长为b,则= .
12.如图所示,⊙O的半径为5,AB为弦,半径OC⊥AB,垂足为D,如果CD=2,那么AB的长是 .
13.抛物线y=﹣x2﹣2x+3与x轴交于A、B两点,若一个半径为的圆也经过点A、B,则该圆的圆心为 .
14.如图,边长为4的正六边形ABCDEF内接于⊙O,则⊙O的内接正三角形ACE的边长为 .
三、解答题
15.如图,在△ABC中,以AB为直径的⊙O交AC于点M,弦MN∥BC交AB于点E,且ME=3,AE=4,AM=5.
(1)求证:BC是⊙O的切线;
(2)求⊙O的直径AB的长度.
16.如图,有一拱桥的桥拱是圆弧形,已知桥拱的水面跨度AB(弧所对的弦的长)为8米,拱高CD(弧的中点到弦的距离)为2米.
(1)求桥拱所在圆的半径长;
(2)如果水面AB上升到EF时,从点E测得桥顶D的仰角为α,且cotα=3,求水面上升的高度.
17.如图,在Rt△ABC中,∠ABC=90°,AB=CB,以AB为直径的⊙O交AC于点D,点E是AB边上一点(点E不与点A,B重合),DE的延长线交⊙O于点G,DF⊥DG,且交BC于点F.
(1)求证:AE=BF.
(2)连接GB,EF,求证:GB∥EF.
(3)若AE=2,EB=4,求DG的长.
18.已知:如图,四边形ABCD内接于⊙O,AC和BD相交于E,BC=CD=4,AE=6,且BE和DE的长是正整数,求BD的长.
19.如图:△ABC是⊙O的内接三角形,∠ACB=45°,∠AOC=150°,过点C作⊙O的切线交AB的延长线于点D.
(1)求证:CD=CB;
(2)如果⊙O的半径为2,求AC的长.
20.如图已知⊙O经过A、B两点,AB=6,C是的中点,联结OC交弦AB与点D,CD=1.
(1)求圆⊙O的半径;
(2)过点B、点O分别作点AO、AB的平行线,交于点G,E是⊙O上一点,联结EG交⊙O于点F,当EF=AB,求sin∠OGE的值.
答案
一、选择题
B.C.C.B.C.D.
二、填空题
7.10﹣2.
8..
9.6.
10.(0,1).
11..
12.8.
13.(﹣1,1)或(﹣1,﹣1).
14.4.
三、解答题
15.(1)证明:∵在△AME中,ME=3,AE=4,AM=5,
∴AM2=ME2+AE2,
∴△AME是直角三角形,
∴∠AEM=90°,
又∵MN∥BC,
∴∠ABC=∠AEM=90°,
∴AB⊥BC,
∵AB为直径,
∴BC是⊙O的切线;
(2)解:连接OM,如图,设⊙O的半径是r,
在Rt△OEM中,OE=AE﹣OA=4﹣r,ME=3,OM=r,
∵OM2=ME2+OE2,
∴r2=32+(4﹣r)2,
解得:r=,
∴AB=2r=.
16.解:(1)∵,DC⊥AB,
∴AC=BC,DC经过圆心,
设拱桥的桥拱弧AB所在圆的圆心为O,
∵AB=8,
∴AC=BC=4,
联结OA,设半径OA=OD=R,OC=OD﹣DC=R﹣2,
∵OD⊥AB,
∴∠ACO=90°,
在Rt△ACO中,∵OA2=AC2+OC2,
∴R2=(R﹣2)2+42,
解之得R=5.
答:桥拱所在圆的半径长为5米.
(2)设OD与EF相交于点G,联结OE,
∵EF∥AB,OD⊥AB,
∴OD⊥EF,
∴∠EGD=∠EGO=90°,
在Rt△EGD中,,
∴EG=3DG,
设水面上升的高度为x米,即CG=x,则DG=2﹣x,
∴EG=6﹣3x,
在Rt△EGO中,∵EG2+OG2=OE2,
∴(6﹣3x)2+(3+x)2=52,
化简得 x2﹣3x+2=0,解得 x1=2(舍去),x2=1,
答:水面上升的高度为1米.
17.(1)证明:连接BD.如图,
在Rt△ABC中,∠ABC=90°,AB=BC,
∴∠A=∠C=45°.
∵AB是⊙O的直径,
∴∠ADB=90°,即BD⊥AC,
∴BD=AD=CD,∠CBD=∠C=45°,
∵DF⊥DG,∠FDG=90°,
∴∠FDB+∠BDG=90°,
又∵∠EDA+∠BDG=90°,
∴∠EDA=∠FDB,
在△AED和△BFD中,
∴△AED≌△BFD(ASA),
∴AE=BF;
(2)证明:如图,由(1)知△AED≌△BFD,
∴DE=DF.
∵∠EDF=90°.
∴△EDF是等腰直角三角形,
∴∠DEF=45°,
∵∠G=∠A=45°.
∴∠G=∠DEF,
∴GB∥EF;
(3)解:∵AE=BF,AE=2,
∴BF=2.
在Rt△EBF中,EF==2,
∵△DED为等腰直角三角形,∠EDF=90°,
∴DE=EF=×2=,
∵∠G=∠A,∠GEB=∠AED,
∴△GEB∽△AED,
∴,即GE DE=AE BE,
∴GE==,
∴DG=GE+ED=+=.
18.解:∵BC=CD=4,
∴,
∴∠CBE=∠CDB=∠CAB,
又∵∠BCE=∠ACB,
∴△CBE∽△CAB,
∴=,即=,
整理得:EC2+6EC﹣16=0,
解得:EC=2,或EC=﹣8(舍去),
∴EC=2,
由相交弦定理得:BE×ED=AE×EC,
∴BE×ED=2×6=12,
∵BE和DE的长是正整数,
∴BE和DE的取值分别为3,4或2,6或1,12;
∵BC=CD=4,
∴BD<BC+CD=4+4=8,
∴BD=3+4=7.
19.(1)证明:连接OB,则∠AOB=2∠ACB=2×45°=90°,
∵OA=OB,
∴∠OAB=OBA=45°,
∵∠AOC=150°,OA=OC,
∴∠OCA=∠OAC=15°,
∴∠OCB=∠OCA+∠ACB=60°,
∴△OBC是等边三角形,
∴∠BOC=∠OBC=60°,
∴∠CBD=180°﹣∠OBA﹣∠OBC=75°,
∵CD是⊙O的切线,
∴OC⊥CD,
∴∠D=360°﹣∠OBD﹣∠BOC﹣∠OCD=360°﹣(60°+75°)﹣60°﹣90°=75°,
∴∠CBD=∠D,
∴CB=CD;
(2)在Rt△AOB中,AB=OA=2,
∵CD是⊙O的切线,
∴∠DCB=∠CAD,
∵∠D是公共角,
∴△DBC∽△DCA,
∴=
∴CD2=AD BD=BD (BD+AB),
∵CD=BC=OC=2,
∴4=BD (2+BD),
解得:BD=﹣,
∴AC=AD=AB+BD=+.
20.解:(1)∵AB=6,C是的中点,CD=1,
∴OC⊥AB且OC平分AB,
∴AD=3,∠ODA=90°,
设OA=r,则OD=r﹣1,
∴r2=32+(r﹣1)2,
解得,r=5,
即圆⊙O的半径为5;
(2)作OH⊥EF于点H,
∵AB=EF,OD=r﹣1=4,
∴OH=OD=4,∠OHG=90°,
∵OA∥BG,OG∥AB,
∴四边形OABG是平行四边形,
∴OG=AB,
∵AB=6,
∴OG=6,
∴sin∠OGH===,
即sin∠OGE=.
