沪科版九年级数学下册试题 24.3 圆周角 一课一练(含答案)
文档属性
| 名称 | 沪科版九年级数学下册试题 24.3 圆周角 一课一练(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 211.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-29 00:00:00 | ||
图片预览



文档简介
24.3 圆周角
一、选择题
1.如图,△ABC是⊙O的内接三角形,半径OB=3,sinA=,则弦BC的长为( )
A.3 B.4 C.5 D.3.75
2.如图,半径为5的⊙A经过点C和点O,点B是y轴右侧⊙A的优弧上一点,∠OBC=30°,则点C的坐标为( )
A.(0,5) B.(0,5) C.(0,) D.(0,)
3.如图,AB是⊙O的直径,且经过弦CD的中点H,已知tan∠CDB=,BD=10,则OH的长度为( )
A. B.1 C. D.
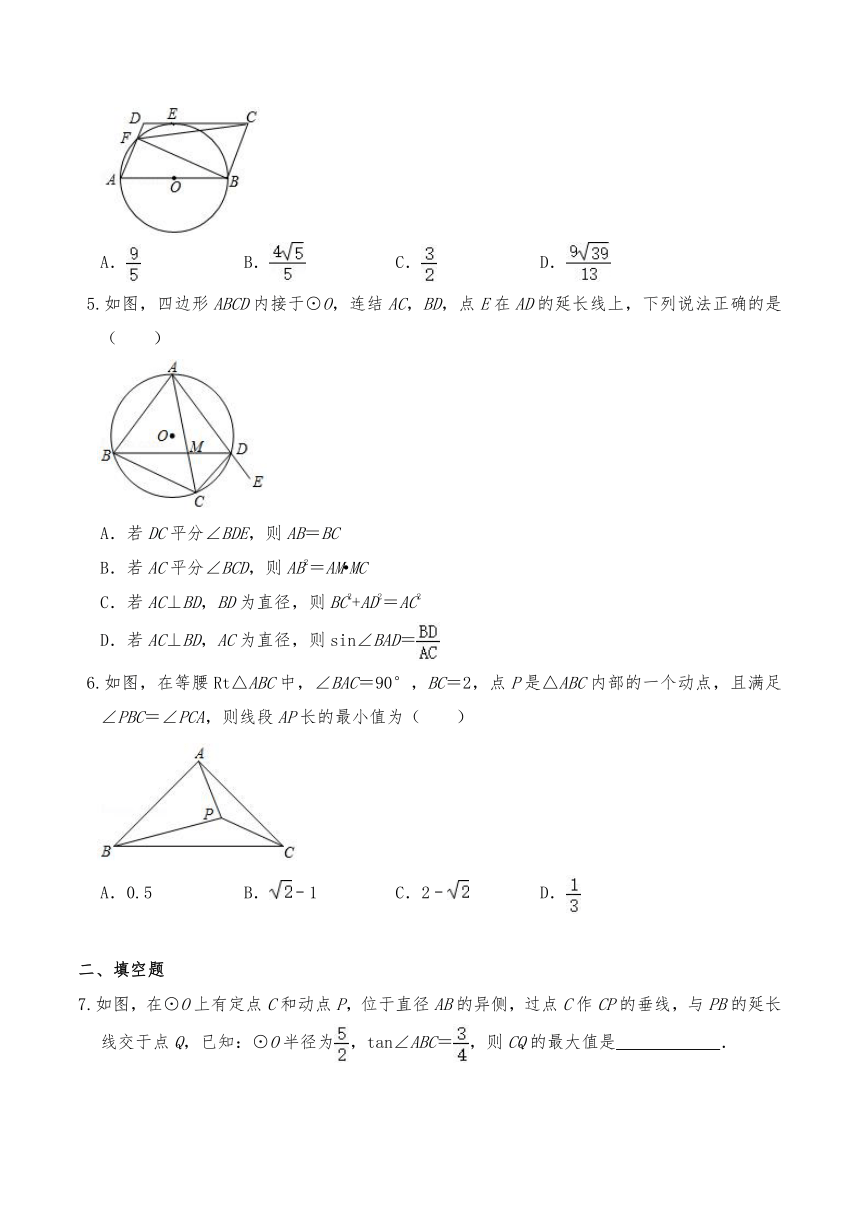
4.如图,四边形ABCD是平行四边形,以AB为直径的⊙O与CD切于点E,AD交⊙O于点F.连接CF,若CE=2DE,则tan∠DFC的值为( )
A. B. C. D.
5.如图,四边形ABCD内接于⊙O,连结AC,BD,点E在AD的延长线上,下列说法正确的是( )
A.若DC平分∠BDE,则AB=BC
B.若AC平分∠BCD,则AB2=AM MC
C.若AC⊥BD,BD为直径,则BC2+AD2=AC2
D.若AC⊥BD,AC为直径,则sin∠BAD=
6.如图,在等腰Rt△ABC中,∠BAC=90°,BC=2,点P是△ABC内部的一个动点,且满足∠PBC=∠PCA,则线段AP长的最小值为( )
A.0.5 B.﹣1 C.2﹣ D.
二、填空题
7.如图,在⊙O上有定点C和动点P,位于直径AB的异侧,过点C作CP的垂线,与PB的延长线交于点Q,已知:⊙O半径为,tan∠ABC=,则CQ的最大值是 .
8.如图,四边形ABCD是⊙O的内接矩形,将矩形ABCD沿着直线BC翻折,点A、点D的对应点分别为A′、D′,如果直线A′D′与⊙O相切,那么的值为 .
9.如果一个四边形有且只有三个顶点在圆上,那么称这个四边形是该圆的“联络四边形”,已知圆的半径长为5,这个圆的一个联络四边形是边长为2的菱形,那么这个菱形不在圆上的顶点与圆心的距离是 .
10.如图,定直线l经过圆心O,P是半径OA上一动点,AC⊥l于点C,当半径OA绕着点O旋转时,总有OP=OC,若OA绕点O旋转60°时,P、A两点的运动路径长的比值是 .
11.如图,在⊙O中,弦AB=4,点C是上的动点(不为A,B),且∠ACB=120°,则CA+CB的最大值为 .
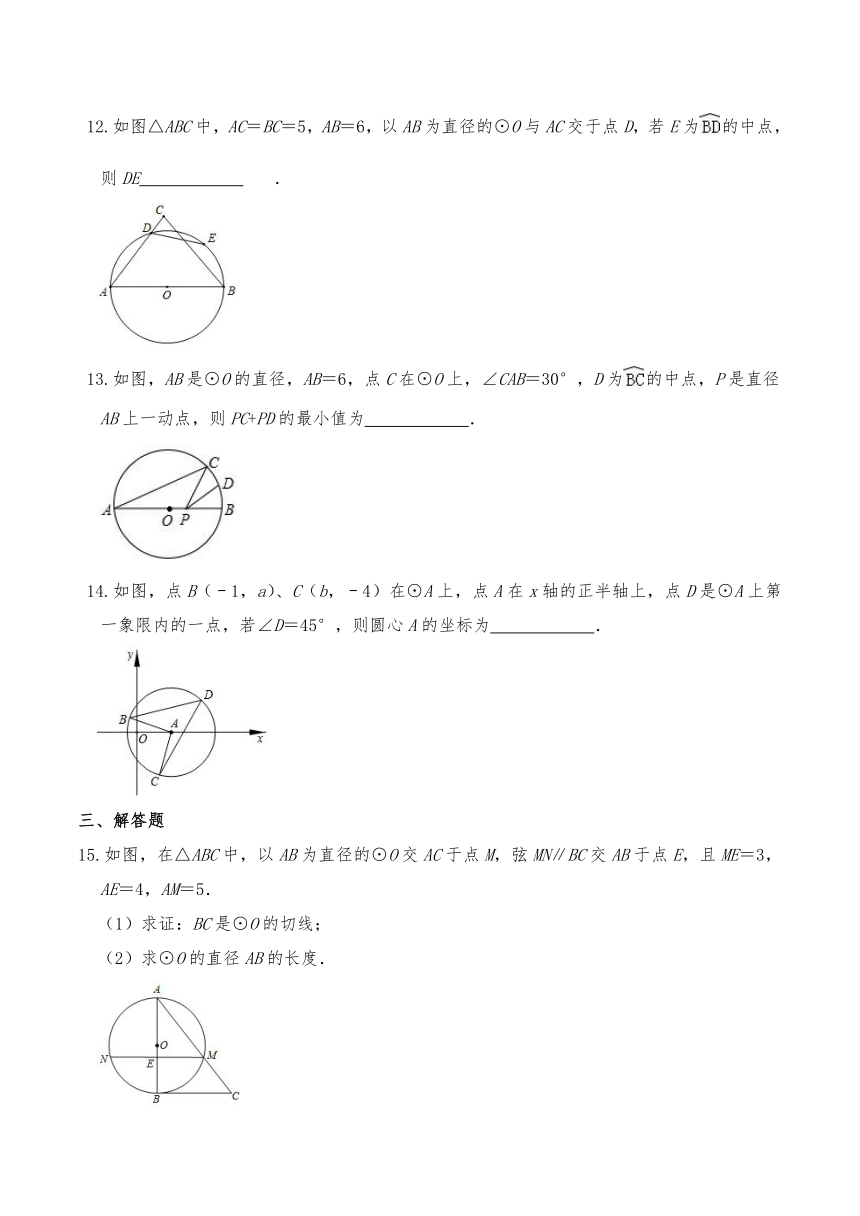
12.如图△ABC中,AC=BC=5,AB=6,以AB为直径的⊙O与AC交于点D,若E为的中点,则DE .
13.如图,AB是⊙O的直径,AB=6,点C在⊙O上,∠CAB=30°,D为的中点,P是直径AB上一动点,则PC+PD的最小值为 .
14.如图,点B(﹣1,a)、C(b,﹣4)在⊙A上,点A在x轴的正半轴上,点D是⊙A上第一象限内的一点,若∠D=45°,则圆心A的坐标为 .
三、解答题
15.如图,在△ABC中,以AB为直径的⊙O交AC于点M,弦MN∥BC交AB于点E,且ME=3,AE=4,AM=5.
(1)求证:BC是⊙O的切线;
(2)求⊙O的直径AB的长度.
16.如图,在Rt△ABC中,∠ABC=90°,AB=CB,以AB为直径的⊙O交AC于点D,点E是AB边上一点(点E不与点A,B重合),DE的延长线交⊙O于点G,DF⊥DG,且交BC于点F.
(1)求证:AE=BF.
(2)连接GB,EF,求证:GB∥EF.
(3)若AE=2,EB=4,求DG的长.
17.如图,已知AB、AC是⊙O的两条弦,且AO平分∠BAC.点M、N分别在弦AB、AC上,满足AM=CN.
(1)求证:AB=AC;
(2)联结OM、ON、MN,求证:=.
18.如图,PA是⊙O的切线,A是切点,AC是直径,AB是弦,连接PB、PC,PC交AB于点E,且PA=PB.
(1)求证:PB是⊙O的切线;
(2)若CP平分∠OPB,求的值.
19.已知AB是⊙O的直径,C为⊙O上一点,∠OAC=58°.
(Ⅰ)如图①,过点C作⊙O的切线,与BA的延长线交于点P,求∠P的大小;
(Ⅱ)如图②,P为AB上一点,CP延长线与⊙O交于点Q.若AQ=CQ,求∠APC的大小.
20.如图,已知AB是圆O的直径,AC、BC是圆O的弦,OM∥AC交圆O于M,交BC于E,过点B作圆O的切线交OE的延长线于点D,连接DC并延长交BA的延长线于点F.
(1)求证:DC是圆O的切线;
(2)当∠BAC= 时,四边形OBMC为菱形.
答案
一、选择题
B.A.A.A.D.C.
二、填空题
7..
8..
9.1.
10.1.
11.8.
12..
13.3.
14.(3,0).
三、解答题
15.(1)证明:∵在△AME中,ME=3,AE=4,AM=5,
∴AM2=ME2+AE2,
∴△AME是直角三角形,
∴∠AEM=90°,
又∵MN∥BC,
∴∠ABC=∠AEM=90°,
∴AB⊥BC,
∵AB为直径,
∴BC是⊙O的切线;
(2)解:连接OM,如图,设⊙O的半径是r,
在Rt△OEM中,OE=AE﹣OA=4﹣r,ME=3,OM=r,
∵OM2=ME2+OE2,
∴r2=32+(4﹣r)2,
解得:r=,
∴AB=2r=.
16.(1)证明:连接BD.如图,
在Rt△ABC中,∠ABC=90°,AB=BC,
∴∠A=∠C=45°.
∵AB是⊙O的直径,
∴∠ADB=90°,即BD⊥AC,
∴BD=AD=CD,∠CBD=∠C=45°,
∵DF⊥DG,∠FDG=90°,
∴∠FDB+∠BDG=90°,
又∵∠EDA+∠BDG=90°,
∴∠EDA=∠FDB,
在△AED和△BFD中,
∴△AED≌△BFD(ASA),
∴AE=BF;
(2)证明:如图,由(1)知△AED≌△BFD,
∴DE=DF.
∵∠EDF=90°.
∴△EDF是等腰直角三角形,
∴∠DEF=45°,
∵∠G=∠A=45°.
∴∠G=∠DEF,
∴GB∥EF;
(3)解:∵AE=BF,AE=2,
∴BF=2.
在Rt△EBF中,EF==2,
∵△DED为等腰直角三角形,∠EDF=90°,
∴DE=EF=×2=,
∵∠G=∠A,∠GEB=∠AED,
∴△GEB∽△AED,
∴,即GE DE=AE BE,
∴GE==,
∴DG=GE+ED=+=.
17.证明:(1)过点O作OD⊥AB于点D,OE⊥AC于点E,如图所示:
∵AO平分∠BAC.
∴OD=OE,
∴AB=AC;
(2)联结OB,OM,ON,MN,如图所示,
∵AM=CN,AB=AC
∴BM=AN,
∵OA=OB,
∴∠B=∠BAO,
∵∠BAO=∠OAN,
∴∠B=∠OAN,
∴△BOM≌△AON(SAS),
∴∠BOM=∠AON,OM=ON,
∴∠AOB=∠MON,
∴△NOM∽△BOA,
∴.
18.证明:(1)连接OB,BC,设AB与OP交于点K,
∵PA是⊙O的切线,
∴∠OAP=90°,
∵PA=PB,
∴∠PBA=∠PAB,
∵OA=OB,
∴∠OAB=∠OBA,
∴∠OAB+∠PAB=∠OBA+∠PBA,
∴∠PAO=∠PBO=90°,且OB是半径,
∴PB是⊙O的切线;
(2)∵PA,PB是⊙O的切线,
∴∠APO=∠BPO,且PA=PB,
∴PO⊥AB,即∠AKO=90°,
∵AC是直径,
∴∠ABC=90°,
∴OP∥BC,
∴∠OPC=∠PCB,
∵CP平分∠OPB,
∴∠OPC=∠BPC,
∴∠BCP=∠BPC,
∴BP=BC,
∵OP∥BC,
∴,
∴BC=2OK,
∴AP=BP=2OK,
∵∠OAP=∠AKO=90°,∠APO=∠APK,
∴△APK∽△OPA,
∴,
∴AP2=KP OP,
∴4OK2=KP (OK+KP),
∴KP=OK,
∵OP∥BC,
∴=.
19.解:(I)如图①,
∵OA=OC,∠OAC=58°,
∴∠OCA=58°
∴∠COA=180°﹣2×58°=64°
∵PC是⊙O的切线,
∴∠OCP=90°,
∴∠P=90°﹣64°=26°;
(II)∵∠AOC=64°,
∴∠Q=∠AOC=32°,
∵AQ=CQ,
∴∠QAC=∠QCA=74°,
∵∠OCA=58°,
∴∠PCO=74°﹣58°=16°,
∵∠AOC=∠QCO+∠APC,
∴∠APC=64°﹣16°=48°.
20.(1)证明:OM∥AC,
∴∠OEB=∠ACB,
∵AB是圆O的直径,
∴∠OEB=∠ACB=90°,
∴OD⊥BC,由垂径定理得OD垂直平分BC,
∴DB=DC,
∴∠DBE=∠DCE,
又∵OC=OB,
∴∠OBE=∠OCE,
即∠DBO=∠OCD,
∵DB为圆O的切线,OB是半径,
∴∠DBO=90°,
∴∠OCD=∠DBO=90°,
即OC⊥DC,
∵OC是圆O的半径,
∴DC是圆O的切线;
(2)当∠BAC=60°时,四边形OBMC为菱形;
理由:∵∠BAC=60°,
∴∠BOC=120°,
∵OD垂直平分BC,OC=OB,
∴∠COM=∠BOM=60°,
∴△COM和△BOM是等边三角形,
∴OC=OB=CM=BM,
∴四边形OBMC为菱形.
故答案为:60°.
一、选择题
1.如图,△ABC是⊙O的内接三角形,半径OB=3,sinA=,则弦BC的长为( )
A.3 B.4 C.5 D.3.75
2.如图,半径为5的⊙A经过点C和点O,点B是y轴右侧⊙A的优弧上一点,∠OBC=30°,则点C的坐标为( )
A.(0,5) B.(0,5) C.(0,) D.(0,)
3.如图,AB是⊙O的直径,且经过弦CD的中点H,已知tan∠CDB=,BD=10,则OH的长度为( )
A. B.1 C. D.
4.如图,四边形ABCD是平行四边形,以AB为直径的⊙O与CD切于点E,AD交⊙O于点F.连接CF,若CE=2DE,则tan∠DFC的值为( )
A. B. C. D.
5.如图,四边形ABCD内接于⊙O,连结AC,BD,点E在AD的延长线上,下列说法正确的是( )
A.若DC平分∠BDE,则AB=BC
B.若AC平分∠BCD,则AB2=AM MC
C.若AC⊥BD,BD为直径,则BC2+AD2=AC2
D.若AC⊥BD,AC为直径,则sin∠BAD=
6.如图,在等腰Rt△ABC中,∠BAC=90°,BC=2,点P是△ABC内部的一个动点,且满足∠PBC=∠PCA,则线段AP长的最小值为( )
A.0.5 B.﹣1 C.2﹣ D.
二、填空题
7.如图,在⊙O上有定点C和动点P,位于直径AB的异侧,过点C作CP的垂线,与PB的延长线交于点Q,已知:⊙O半径为,tan∠ABC=,则CQ的最大值是 .
8.如图,四边形ABCD是⊙O的内接矩形,将矩形ABCD沿着直线BC翻折,点A、点D的对应点分别为A′、D′,如果直线A′D′与⊙O相切,那么的值为 .
9.如果一个四边形有且只有三个顶点在圆上,那么称这个四边形是该圆的“联络四边形”,已知圆的半径长为5,这个圆的一个联络四边形是边长为2的菱形,那么这个菱形不在圆上的顶点与圆心的距离是 .
10.如图,定直线l经过圆心O,P是半径OA上一动点,AC⊥l于点C,当半径OA绕着点O旋转时,总有OP=OC,若OA绕点O旋转60°时,P、A两点的运动路径长的比值是 .
11.如图,在⊙O中,弦AB=4,点C是上的动点(不为A,B),且∠ACB=120°,则CA+CB的最大值为 .
12.如图△ABC中,AC=BC=5,AB=6,以AB为直径的⊙O与AC交于点D,若E为的中点,则DE .
13.如图,AB是⊙O的直径,AB=6,点C在⊙O上,∠CAB=30°,D为的中点,P是直径AB上一动点,则PC+PD的最小值为 .
14.如图,点B(﹣1,a)、C(b,﹣4)在⊙A上,点A在x轴的正半轴上,点D是⊙A上第一象限内的一点,若∠D=45°,则圆心A的坐标为 .
三、解答题
15.如图,在△ABC中,以AB为直径的⊙O交AC于点M,弦MN∥BC交AB于点E,且ME=3,AE=4,AM=5.
(1)求证:BC是⊙O的切线;
(2)求⊙O的直径AB的长度.
16.如图,在Rt△ABC中,∠ABC=90°,AB=CB,以AB为直径的⊙O交AC于点D,点E是AB边上一点(点E不与点A,B重合),DE的延长线交⊙O于点G,DF⊥DG,且交BC于点F.
(1)求证:AE=BF.
(2)连接GB,EF,求证:GB∥EF.
(3)若AE=2,EB=4,求DG的长.
17.如图,已知AB、AC是⊙O的两条弦,且AO平分∠BAC.点M、N分别在弦AB、AC上,满足AM=CN.
(1)求证:AB=AC;
(2)联结OM、ON、MN,求证:=.
18.如图,PA是⊙O的切线,A是切点,AC是直径,AB是弦,连接PB、PC,PC交AB于点E,且PA=PB.
(1)求证:PB是⊙O的切线;
(2)若CP平分∠OPB,求的值.
19.已知AB是⊙O的直径,C为⊙O上一点,∠OAC=58°.
(Ⅰ)如图①,过点C作⊙O的切线,与BA的延长线交于点P,求∠P的大小;
(Ⅱ)如图②,P为AB上一点,CP延长线与⊙O交于点Q.若AQ=CQ,求∠APC的大小.
20.如图,已知AB是圆O的直径,AC、BC是圆O的弦,OM∥AC交圆O于M,交BC于E,过点B作圆O的切线交OE的延长线于点D,连接DC并延长交BA的延长线于点F.
(1)求证:DC是圆O的切线;
(2)当∠BAC= 时,四边形OBMC为菱形.
答案
一、选择题
B.A.A.A.D.C.
二、填空题
7..
8..
9.1.
10.1.
11.8.
12..
13.3.
14.(3,0).
三、解答题
15.(1)证明:∵在△AME中,ME=3,AE=4,AM=5,
∴AM2=ME2+AE2,
∴△AME是直角三角形,
∴∠AEM=90°,
又∵MN∥BC,
∴∠ABC=∠AEM=90°,
∴AB⊥BC,
∵AB为直径,
∴BC是⊙O的切线;
(2)解:连接OM,如图,设⊙O的半径是r,
在Rt△OEM中,OE=AE﹣OA=4﹣r,ME=3,OM=r,
∵OM2=ME2+OE2,
∴r2=32+(4﹣r)2,
解得:r=,
∴AB=2r=.
16.(1)证明:连接BD.如图,
在Rt△ABC中,∠ABC=90°,AB=BC,
∴∠A=∠C=45°.
∵AB是⊙O的直径,
∴∠ADB=90°,即BD⊥AC,
∴BD=AD=CD,∠CBD=∠C=45°,
∵DF⊥DG,∠FDG=90°,
∴∠FDB+∠BDG=90°,
又∵∠EDA+∠BDG=90°,
∴∠EDA=∠FDB,
在△AED和△BFD中,
∴△AED≌△BFD(ASA),
∴AE=BF;
(2)证明:如图,由(1)知△AED≌△BFD,
∴DE=DF.
∵∠EDF=90°.
∴△EDF是等腰直角三角形,
∴∠DEF=45°,
∵∠G=∠A=45°.
∴∠G=∠DEF,
∴GB∥EF;
(3)解:∵AE=BF,AE=2,
∴BF=2.
在Rt△EBF中,EF==2,
∵△DED为等腰直角三角形,∠EDF=90°,
∴DE=EF=×2=,
∵∠G=∠A,∠GEB=∠AED,
∴△GEB∽△AED,
∴,即GE DE=AE BE,
∴GE==,
∴DG=GE+ED=+=.
17.证明:(1)过点O作OD⊥AB于点D,OE⊥AC于点E,如图所示:
∵AO平分∠BAC.
∴OD=OE,
∴AB=AC;
(2)联结OB,OM,ON,MN,如图所示,
∵AM=CN,AB=AC
∴BM=AN,
∵OA=OB,
∴∠B=∠BAO,
∵∠BAO=∠OAN,
∴∠B=∠OAN,
∴△BOM≌△AON(SAS),
∴∠BOM=∠AON,OM=ON,
∴∠AOB=∠MON,
∴△NOM∽△BOA,
∴.
18.证明:(1)连接OB,BC,设AB与OP交于点K,
∵PA是⊙O的切线,
∴∠OAP=90°,
∵PA=PB,
∴∠PBA=∠PAB,
∵OA=OB,
∴∠OAB=∠OBA,
∴∠OAB+∠PAB=∠OBA+∠PBA,
∴∠PAO=∠PBO=90°,且OB是半径,
∴PB是⊙O的切线;
(2)∵PA,PB是⊙O的切线,
∴∠APO=∠BPO,且PA=PB,
∴PO⊥AB,即∠AKO=90°,
∵AC是直径,
∴∠ABC=90°,
∴OP∥BC,
∴∠OPC=∠PCB,
∵CP平分∠OPB,
∴∠OPC=∠BPC,
∴∠BCP=∠BPC,
∴BP=BC,
∵OP∥BC,
∴,
∴BC=2OK,
∴AP=BP=2OK,
∵∠OAP=∠AKO=90°,∠APO=∠APK,
∴△APK∽△OPA,
∴,
∴AP2=KP OP,
∴4OK2=KP (OK+KP),
∴KP=OK,
∵OP∥BC,
∴=.
19.解:(I)如图①,
∵OA=OC,∠OAC=58°,
∴∠OCA=58°
∴∠COA=180°﹣2×58°=64°
∵PC是⊙O的切线,
∴∠OCP=90°,
∴∠P=90°﹣64°=26°;
(II)∵∠AOC=64°,
∴∠Q=∠AOC=32°,
∵AQ=CQ,
∴∠QAC=∠QCA=74°,
∵∠OCA=58°,
∴∠PCO=74°﹣58°=16°,
∵∠AOC=∠QCO+∠APC,
∴∠APC=64°﹣16°=48°.
20.(1)证明:OM∥AC,
∴∠OEB=∠ACB,
∵AB是圆O的直径,
∴∠OEB=∠ACB=90°,
∴OD⊥BC,由垂径定理得OD垂直平分BC,
∴DB=DC,
∴∠DBE=∠DCE,
又∵OC=OB,
∴∠OBE=∠OCE,
即∠DBO=∠OCD,
∵DB为圆O的切线,OB是半径,
∴∠DBO=90°,
∴∠OCD=∠DBO=90°,
即OC⊥DC,
∵OC是圆O的半径,
∴DC是圆O的切线;
(2)当∠BAC=60°时,四边形OBMC为菱形;
理由:∵∠BAC=60°,
∴∠BOC=120°,
∵OD垂直平分BC,OC=OB,
∴∠COM=∠BOM=60°,
∴△COM和△BOM是等边三角形,
∴OC=OB=CM=BM,
∴四边形OBMC为菱形.
故答案为:60°.
