沪科版九年级数学下册试题 24.4直线与圆的位置关系 一课一练(含答案)
文档属性
| 名称 | 沪科版九年级数学下册试题 24.4直线与圆的位置关系 一课一练(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 228.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-29 00:00:00 | ||
图片预览


文档简介
24.4直线与圆的位置关系
一、选择题
1.如图,∠MON=30°,OP是∠MON的角平分线,PQ∥ON交OM于点Q,以P为圆心半径为4的圆与ON相切,如果以Q为圆心半径为r的圆与⊙P相交,那么r的取值范围是( )
A.4<r<12 B.2<r<12 C.4<r<8 D.r>4
2.如图,⊙O内切于正方形ABCD,O为圆心,作∠MON=90°,其两边分别交BC,CD于点N,M,若CM+CN=4,则⊙O的面积为( )
A.π B.2π C.4π D.0.5π
3.行驶在水平路面上的汽车,若把路面看成直线,则此时转动的车轮与地面的位置关系是( )
A.相交 B.相切 C.相离 D.不确定
4.如图,在平面直角坐标系中,⊙P与y轴相切,直线y=x被⊙P截得的弦AB长为,若点P的坐标为(4,p),则p的值为( )
A. B. C. D.
5.在平面直角坐标系中,点A(0,2)、B(a,a+2)、C(b,0)(a>0,b>0),若AB=4且∠ACB最大时,b的值为( )
A.2+2 B.﹣2+2 C.2+4 D.﹣2+4
6.如图,在直角坐标系中,⊙A的半径为2,圆心坐标为(4,0),y轴上有点B(0,3),点C是⊙A上的动点,点P是BC的中点,则OP的范围是( )
A.≤OP≤ B.2≤OP≤4 C.≤OP≤ D.3≤OP≤4
二、填空题
7.如图,在△ABC中,AB=5,BC=3,AC=4,以点C为圆心的圆与AB相切,则⊙C的半径为 .
8.如图,OA、OC都是⊙O的半径,点B在OC的延长线上,BA与⊙O相切于点A,连接AC,若AC=2,tan∠BAC=,则⊙O的半径长为 .
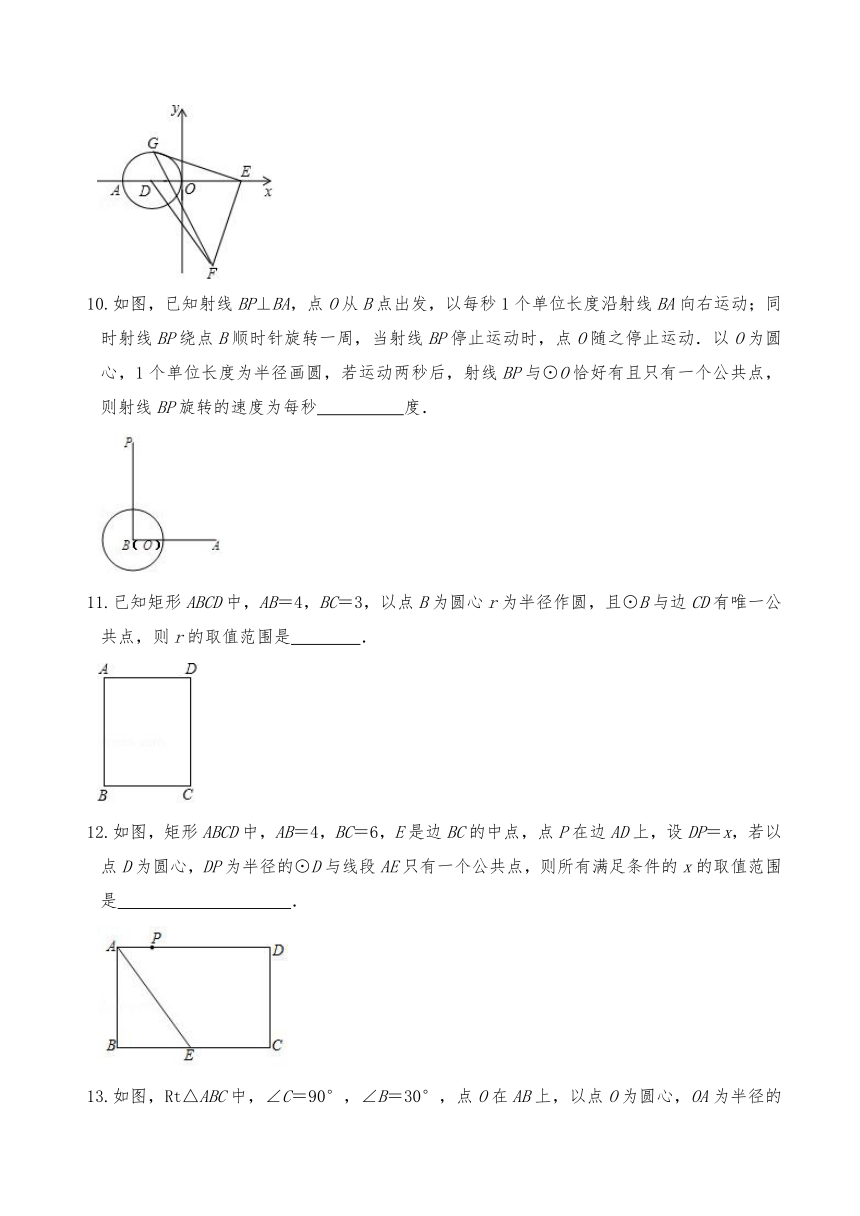
9.如图,平面直角坐标系中,点A(﹣4,0),点E (4,0),以AO为直径作⊙D,点G是⊙D上一动点,以EG为腰向下作等腰直角三角形EGF,连接DF,则DF的最大值是 .
10.如图,已知射线BP⊥BA,点O从B点出发,以每秒1个单位长度沿射线BA向右运动;同时射线BP绕点B顺时针旋转一周,当射线BP停止运动时,点O随之停止运动.以O为圆心,1个单位长度为半径画圆,若运动两秒后,射线BP与⊙O恰好有且只有一个公共点,则射线BP旋转的速度为每秒 度.
11.已知矩形ABCD中,AB=4,BC=3,以点B为圆心r为半径作圆,且⊙B与边CD有唯一公共点,则r的取值范围是 .
12.如图,矩形ABCD中,AB=4,BC=6,E是边BC的中点,点P在边AD上,设DP=x,若以点D为圆心,DP为半径的⊙D与线段AE只有一个公共点,则所有满足条件的x的取值范围是 .
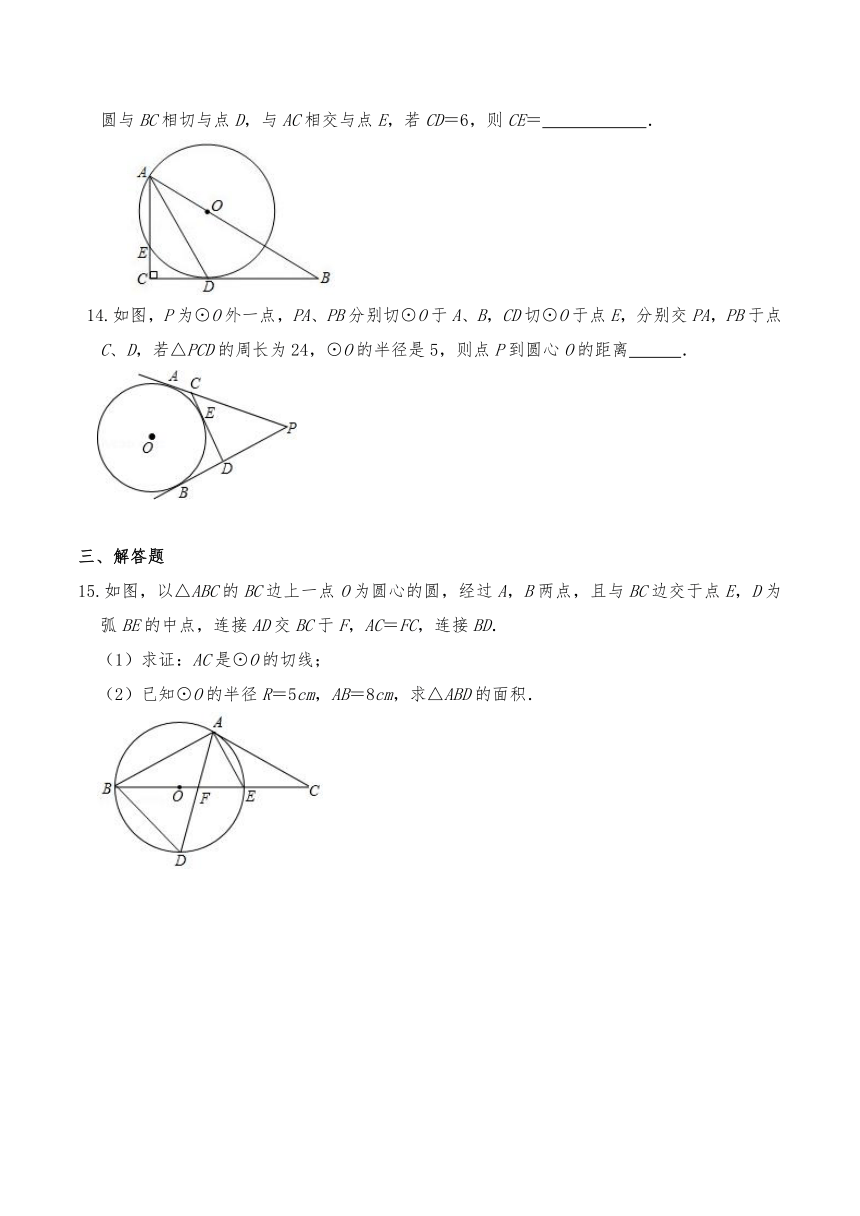
13.如图,Rt△ABC中,∠C=90°,∠B=30°,点O在AB上,以点O为圆心,OA为半径的圆与BC相切与点D,与AC相交与点E,若CD=6,则CE= .
14.如图,P为⊙O外一点,PA、PB分别切⊙O于A、B,CD切⊙O于点E,分别交PA,PB于点C、D,若△PCD的周长为24,⊙O的半径是5,则点P到圆心O的距离 .
三、解答题
15.如图,以△ABC的BC边上一点O为圆心的圆,经过A,B两点,且与BC边交于点E,D为弧BE的中点,连接AD交BC于F,AC=FC,连接BD.
(1)求证:AC是⊙O的切线;
(2)已知⊙O的半径R=5cm,AB=8cm,求△ABD的面积.
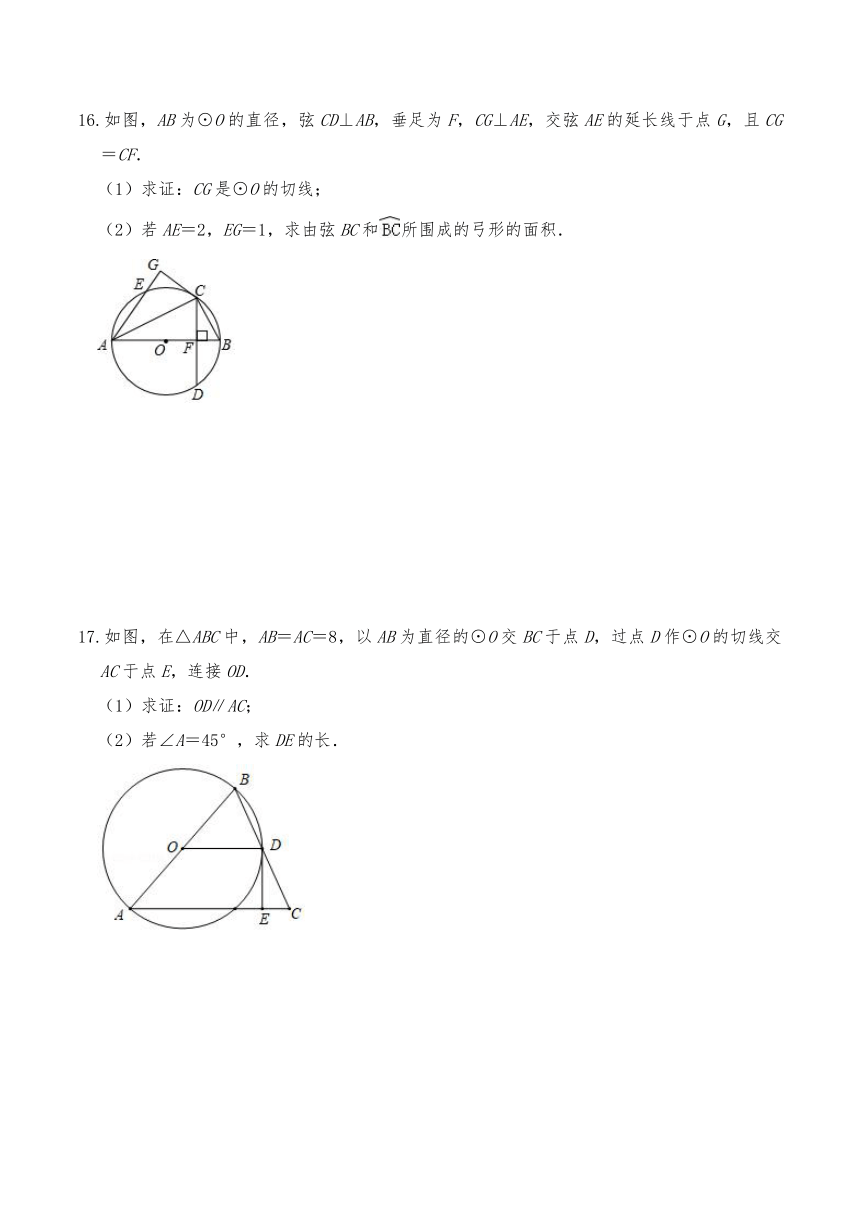
16.如图,AB为⊙O的直径,弦CD⊥AB,垂足为F,CG⊥AE,交弦AE的延长线于点G,且CG=CF.
(1)求证:CG是⊙O的切线;
(2)若AE=2,EG=1,求由弦BC和所围成的弓形的面积.
17.如图,在△ABC中,AB=AC=8,以AB为直径的⊙O交BC于点D,过点D作⊙O的切线交AC于点E,连接OD.
(1)求证:OD∥AC;
(2)若∠A=45°,求DE的长.
18.如图1,在⊙O中,AB为直径,BC为切线,弦BE⊥OC,连CE.
(1)求证:CE为⊙O的切线;
(2)如图2,CF⊥BC交AE的延长线于F,BC=AB,求的值.
19.如图,AB为⊙O的直径,弦CD⊥AB,垂足为点P,直线BF与AD延长线交于点F,且∠AFB=∠ABC.
(1)求证:直线BF是⊙O的切线;
(2)若CD=2,BP=1,求⊙O的半径.
20.在⊙O中,直径AB⊥弦CD于点F,点E是弧AD上一点,连BE交CD于点N,点P在CD的延长线上,PN=PE.
(1)求证:PE是⊙O的切线;
(2)连接DE,若DE∥AB,OF=3,BF=2,求PN的长.
答案
一、选择题
A.C.B.B.B.A.
二、填空题
7. 2.4
8..
9.6+2.
10.30或60.
11.3≤r≤5
12.x=或5<x≤6.
13.2.
14.13.
三、解答题
15.(1)证明:连接OA,OD.
∵点D是弧BE的中点,
∴∠BOD=∠EOD=90°,
∴∠ODF+∠OFD=90°
又∵∠OFD=∠AFC,
∴∠ODF+∠AFC=90°
又∵AC=FC,
∴∠AFC=∠CAF,
∵OA=OD,
∴∠ODF=∠OAF,
∴∠OAF+∠CAF=90°,
即∠OAC=90°,
故AC是⊙O的切线;
(2)解:过点B作BG⊥AD于G,
∵∠BOD=90°,OB=OD=R=5,
∴,
∵点D是弧BE的中点,
∴∠BAD=45°,
∵∠AGB=90°,
∴∠ABG=∠BAD=45°,即BG=AG.
∴2BG2=AB2=82,
∴
又∵,
∴
故S△ABD=AD BG==28(cm2).
16.解:(1)证明:连接OC.
∵CD⊥AB,CG⊥AE,CG=CF,
∴∠CAG=∠BAC,∠AFC=∠G=90°,
∵OA=OC,
∴∠ACO=∠BAC.
∴∠CAG=∠ACO,
∴OC∥AG,
∴∠OCG=180°﹣∠G=90°,
∴CG是⊙O的切线;
(2)过点O作OM⊥AE,垂足为M,
则AM=ME=AE=1,∠OMG=∠OCG=∠G=90°.
∴四边形OCGM为矩形,
∴OC=MG=ME+EG=2.
在Rt△AGC和Rt△AFC中
∴Rt△AGC≌Rt△AFC(HL),
∴AF=AG=AE+EG=3,
∴OF=AF﹣OA=1,
在Rt△COF中,∵cos∠COF==.
∴∠COF=60°,CF=OC sin∠COF=2×=,
∴S弓形BC=﹣×2×=π﹣.
17.(1)证明:∵AB=AC,
∴∠B=∠C,
∵OB=OD,
∴∠B=∠ODB,
∴∠C=∠ODB,
∴OD∥AC;
(2)解:过点O作OF⊥AC于点F,
∵DE是⊙O的切线,
∴DE⊥OD.
∵OD∥AC,
∴DE⊥AC.
∴四边形OFED是矩形.
∴OF=DE.
在Rt△AOF中,∠A=45°,
∴OF=OA=2,
∴DE=2.
18.(1)证明:连接OE,如图1所示:
则OB=OE,设OC与BE交于点H,
∵OC⊥BE,∴H为BE的中点,∴OC垂直平分BE,
∴BC=EC,在△OEC和△OBC中,,∴△OEC≌△OBC(SSS),
∴∠OEC=∠OBC,∵BC为切线,AB为直径,
∴∠OBC=90°,∴∠OEC=90°,
∴CE为⊙O的切线;
(2)解:∵AB为直径,
∴∠AEB=90°=∠OHB,
∴OC∥AF,
∵AB⊥BC,CF⊥BC,
∴AB∥CF,
∴四边形AOCF为平行四边形,
∴AF=OC,
∵BE⊥OC,
∴BH=HE,
∴OH是△BAE的中位线,
设OH=x,则AE=2OH=2x,
∠AEB=∠BHC=90°,
∠BCH=∠ABE=90°﹣∠CBH,
在△ABE和△BCH中,,
∴△ABE≌△BCH(AAS),
∴BH=AE=2x,
∴OB===x,
∴BC=AB=2OB=2x,
∴OC===5x,
∴AF=OC=5x,
EF=AF﹣AE=5x﹣2x=3x,
∴==.
19.(1)证明:∵弧AC=弧AC,
∴∠ABC=∠ADC,
∵∠AFB=∠ABC,
∴∠ADC=∠AFB,
∴CD∥BF,
∵CD⊥AB,
∴AB⊥BF,
∵AB是圆的直径,
∴直线BF是⊙O的切线;
(2)解:设⊙O的半径为r,连接OD.如图所示:
∵AB⊥BF,CD=2,
∴PD=PC=CD=,
∵BP=1,
∴OP=r﹣1
在Rt△OPD中,由勾股定理得:r2 =(r﹣1)2+()2
解得:r=3.
即⊙O的半径为3.
20.(1)证明:连接OE,如图1所示:
∵PN=PE,
∴∠PEN=∠PNE=∠BNF,
∵OE=OB,
∴∠OEB=∠OBE.
∵AB⊥CD,
∴∠OBE+∠BNF=90°,
∴∠OEB+∠PEN=90°,
即∠OEP=90°,
∴PE⊥OE,
∴PE是⊙O的切线.
(2)解:连接CE,如图2所示:
∵DE∥AB,AB⊥CD,
∴∠EDC=90°
∴CE为⊙O的直径.
∵AB⊥CD,
∴CF=DF,∴DE=2OF=6.
∵OF=3,BF=2,∴OC=OB=5,CE=10,
∴CD===8,
由(1)知PE⊥CE.设PD=x,则PC=x+8.
在Rt△PDE和Rt△PCE中,由勾股定理,得:PD2+DE2=PE2=PC2﹣CE2,
即x2+62=(x+8)2﹣102,
解得:x=,
∴PD=.
∴PE===,
∴PN=PE=.
一、选择题
1.如图,∠MON=30°,OP是∠MON的角平分线,PQ∥ON交OM于点Q,以P为圆心半径为4的圆与ON相切,如果以Q为圆心半径为r的圆与⊙P相交,那么r的取值范围是( )
A.4<r<12 B.2<r<12 C.4<r<8 D.r>4
2.如图,⊙O内切于正方形ABCD,O为圆心,作∠MON=90°,其两边分别交BC,CD于点N,M,若CM+CN=4,则⊙O的面积为( )
A.π B.2π C.4π D.0.5π
3.行驶在水平路面上的汽车,若把路面看成直线,则此时转动的车轮与地面的位置关系是( )
A.相交 B.相切 C.相离 D.不确定
4.如图,在平面直角坐标系中,⊙P与y轴相切,直线y=x被⊙P截得的弦AB长为,若点P的坐标为(4,p),则p的值为( )
A. B. C. D.
5.在平面直角坐标系中,点A(0,2)、B(a,a+2)、C(b,0)(a>0,b>0),若AB=4且∠ACB最大时,b的值为( )
A.2+2 B.﹣2+2 C.2+4 D.﹣2+4
6.如图,在直角坐标系中,⊙A的半径为2,圆心坐标为(4,0),y轴上有点B(0,3),点C是⊙A上的动点,点P是BC的中点,则OP的范围是( )
A.≤OP≤ B.2≤OP≤4 C.≤OP≤ D.3≤OP≤4
二、填空题
7.如图,在△ABC中,AB=5,BC=3,AC=4,以点C为圆心的圆与AB相切,则⊙C的半径为 .
8.如图,OA、OC都是⊙O的半径,点B在OC的延长线上,BA与⊙O相切于点A,连接AC,若AC=2,tan∠BAC=,则⊙O的半径长为 .
9.如图,平面直角坐标系中,点A(﹣4,0),点E (4,0),以AO为直径作⊙D,点G是⊙D上一动点,以EG为腰向下作等腰直角三角形EGF,连接DF,则DF的最大值是 .
10.如图,已知射线BP⊥BA,点O从B点出发,以每秒1个单位长度沿射线BA向右运动;同时射线BP绕点B顺时针旋转一周,当射线BP停止运动时,点O随之停止运动.以O为圆心,1个单位长度为半径画圆,若运动两秒后,射线BP与⊙O恰好有且只有一个公共点,则射线BP旋转的速度为每秒 度.
11.已知矩形ABCD中,AB=4,BC=3,以点B为圆心r为半径作圆,且⊙B与边CD有唯一公共点,则r的取值范围是 .
12.如图,矩形ABCD中,AB=4,BC=6,E是边BC的中点,点P在边AD上,设DP=x,若以点D为圆心,DP为半径的⊙D与线段AE只有一个公共点,则所有满足条件的x的取值范围是 .
13.如图,Rt△ABC中,∠C=90°,∠B=30°,点O在AB上,以点O为圆心,OA为半径的圆与BC相切与点D,与AC相交与点E,若CD=6,则CE= .
14.如图,P为⊙O外一点,PA、PB分别切⊙O于A、B,CD切⊙O于点E,分别交PA,PB于点C、D,若△PCD的周长为24,⊙O的半径是5,则点P到圆心O的距离 .
三、解答题
15.如图,以△ABC的BC边上一点O为圆心的圆,经过A,B两点,且与BC边交于点E,D为弧BE的中点,连接AD交BC于F,AC=FC,连接BD.
(1)求证:AC是⊙O的切线;
(2)已知⊙O的半径R=5cm,AB=8cm,求△ABD的面积.
16.如图,AB为⊙O的直径,弦CD⊥AB,垂足为F,CG⊥AE,交弦AE的延长线于点G,且CG=CF.
(1)求证:CG是⊙O的切线;
(2)若AE=2,EG=1,求由弦BC和所围成的弓形的面积.
17.如图,在△ABC中,AB=AC=8,以AB为直径的⊙O交BC于点D,过点D作⊙O的切线交AC于点E,连接OD.
(1)求证:OD∥AC;
(2)若∠A=45°,求DE的长.
18.如图1,在⊙O中,AB为直径,BC为切线,弦BE⊥OC,连CE.
(1)求证:CE为⊙O的切线;
(2)如图2,CF⊥BC交AE的延长线于F,BC=AB,求的值.
19.如图,AB为⊙O的直径,弦CD⊥AB,垂足为点P,直线BF与AD延长线交于点F,且∠AFB=∠ABC.
(1)求证:直线BF是⊙O的切线;
(2)若CD=2,BP=1,求⊙O的半径.
20.在⊙O中,直径AB⊥弦CD于点F,点E是弧AD上一点,连BE交CD于点N,点P在CD的延长线上,PN=PE.
(1)求证:PE是⊙O的切线;
(2)连接DE,若DE∥AB,OF=3,BF=2,求PN的长.
答案
一、选择题
A.C.B.B.B.A.
二、填空题
7. 2.4
8..
9.6+2.
10.30或60.
11.3≤r≤5
12.x=或5<x≤6.
13.2.
14.13.
三、解答题
15.(1)证明:连接OA,OD.
∵点D是弧BE的中点,
∴∠BOD=∠EOD=90°,
∴∠ODF+∠OFD=90°
又∵∠OFD=∠AFC,
∴∠ODF+∠AFC=90°
又∵AC=FC,
∴∠AFC=∠CAF,
∵OA=OD,
∴∠ODF=∠OAF,
∴∠OAF+∠CAF=90°,
即∠OAC=90°,
故AC是⊙O的切线;
(2)解:过点B作BG⊥AD于G,
∵∠BOD=90°,OB=OD=R=5,
∴,
∵点D是弧BE的中点,
∴∠BAD=45°,
∵∠AGB=90°,
∴∠ABG=∠BAD=45°,即BG=AG.
∴2BG2=AB2=82,
∴
又∵,
∴
故S△ABD=AD BG==28(cm2).
16.解:(1)证明:连接OC.
∵CD⊥AB,CG⊥AE,CG=CF,
∴∠CAG=∠BAC,∠AFC=∠G=90°,
∵OA=OC,
∴∠ACO=∠BAC.
∴∠CAG=∠ACO,
∴OC∥AG,
∴∠OCG=180°﹣∠G=90°,
∴CG是⊙O的切线;
(2)过点O作OM⊥AE,垂足为M,
则AM=ME=AE=1,∠OMG=∠OCG=∠G=90°.
∴四边形OCGM为矩形,
∴OC=MG=ME+EG=2.
在Rt△AGC和Rt△AFC中
∴Rt△AGC≌Rt△AFC(HL),
∴AF=AG=AE+EG=3,
∴OF=AF﹣OA=1,
在Rt△COF中,∵cos∠COF==.
∴∠COF=60°,CF=OC sin∠COF=2×=,
∴S弓形BC=﹣×2×=π﹣.
17.(1)证明:∵AB=AC,
∴∠B=∠C,
∵OB=OD,
∴∠B=∠ODB,
∴∠C=∠ODB,
∴OD∥AC;
(2)解:过点O作OF⊥AC于点F,
∵DE是⊙O的切线,
∴DE⊥OD.
∵OD∥AC,
∴DE⊥AC.
∴四边形OFED是矩形.
∴OF=DE.
在Rt△AOF中,∠A=45°,
∴OF=OA=2,
∴DE=2.
18.(1)证明:连接OE,如图1所示:
则OB=OE,设OC与BE交于点H,
∵OC⊥BE,∴H为BE的中点,∴OC垂直平分BE,
∴BC=EC,在△OEC和△OBC中,,∴△OEC≌△OBC(SSS),
∴∠OEC=∠OBC,∵BC为切线,AB为直径,
∴∠OBC=90°,∴∠OEC=90°,
∴CE为⊙O的切线;
(2)解:∵AB为直径,
∴∠AEB=90°=∠OHB,
∴OC∥AF,
∵AB⊥BC,CF⊥BC,
∴AB∥CF,
∴四边形AOCF为平行四边形,
∴AF=OC,
∵BE⊥OC,
∴BH=HE,
∴OH是△BAE的中位线,
设OH=x,则AE=2OH=2x,
∠AEB=∠BHC=90°,
∠BCH=∠ABE=90°﹣∠CBH,
在△ABE和△BCH中,,
∴△ABE≌△BCH(AAS),
∴BH=AE=2x,
∴OB===x,
∴BC=AB=2OB=2x,
∴OC===5x,
∴AF=OC=5x,
EF=AF﹣AE=5x﹣2x=3x,
∴==.
19.(1)证明:∵弧AC=弧AC,
∴∠ABC=∠ADC,
∵∠AFB=∠ABC,
∴∠ADC=∠AFB,
∴CD∥BF,
∵CD⊥AB,
∴AB⊥BF,
∵AB是圆的直径,
∴直线BF是⊙O的切线;
(2)解:设⊙O的半径为r,连接OD.如图所示:
∵AB⊥BF,CD=2,
∴PD=PC=CD=,
∵BP=1,
∴OP=r﹣1
在Rt△OPD中,由勾股定理得:r2 =(r﹣1)2+()2
解得:r=3.
即⊙O的半径为3.
20.(1)证明:连接OE,如图1所示:
∵PN=PE,
∴∠PEN=∠PNE=∠BNF,
∵OE=OB,
∴∠OEB=∠OBE.
∵AB⊥CD,
∴∠OBE+∠BNF=90°,
∴∠OEB+∠PEN=90°,
即∠OEP=90°,
∴PE⊥OE,
∴PE是⊙O的切线.
(2)解:连接CE,如图2所示:
∵DE∥AB,AB⊥CD,
∴∠EDC=90°
∴CE为⊙O的直径.
∵AB⊥CD,
∴CF=DF,∴DE=2OF=6.
∵OF=3,BF=2,∴OC=OB=5,CE=10,
∴CD===8,
由(1)知PE⊥CE.设PD=x,则PC=x+8.
在Rt△PDE和Rt△PCE中,由勾股定理,得:PD2+DE2=PE2=PC2﹣CE2,
即x2+62=(x+8)2﹣102,
解得:x=,
∴PD=.
∴PE===,
∴PN=PE=.
