沪科版九年级数学下册试题 24.6正多边形与圆 一课一练 (含答案)
文档属性
| 名称 | 沪科版九年级数学下册试题 24.6正多边形与圆 一课一练 (含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 203.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-29 00:00:00 | ||
图片预览


文档简介
24.6正多边形与圆
一、选择题
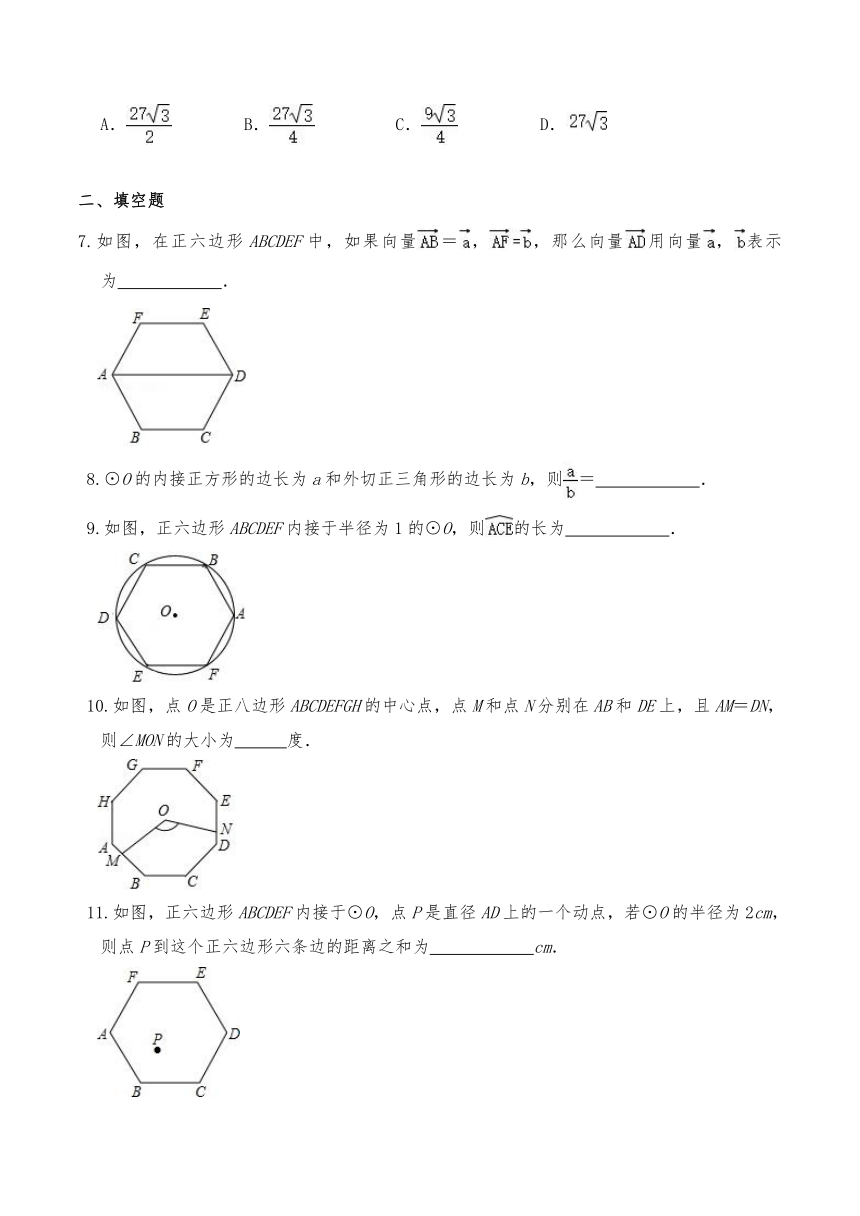
1.如果一个正多边形的外角是锐角,且它的余弦值是,那么它是( )
A.等边三角形 B.正六边形 C.正八边形 D.正十二边形
2.在半径为R的圆上依次截取等于R的弦,顺次连接各分点得到的多边形是( )
A.正三角形 B.正四边形 C.正五边形 D.正六边形
3.如图,在正六边形ABCDEF外作正方形DEGH,连接AH,则tan∠HAB等于( )
A.3 B. C.2 D.
4.如图,⊙O的外切正八边形ABCDEFGH的边长2,则⊙O的半径为( )
A.2 B. C.3 D.
5.已知圆的内接正六边形的面积为18,则该圆的半径等于( )
A.3 B.2 C. D.
6.如图,已知⊙O的周长等于6π,则它的内接正六边形ABCDEF的面积是( )
A. B. C. D.
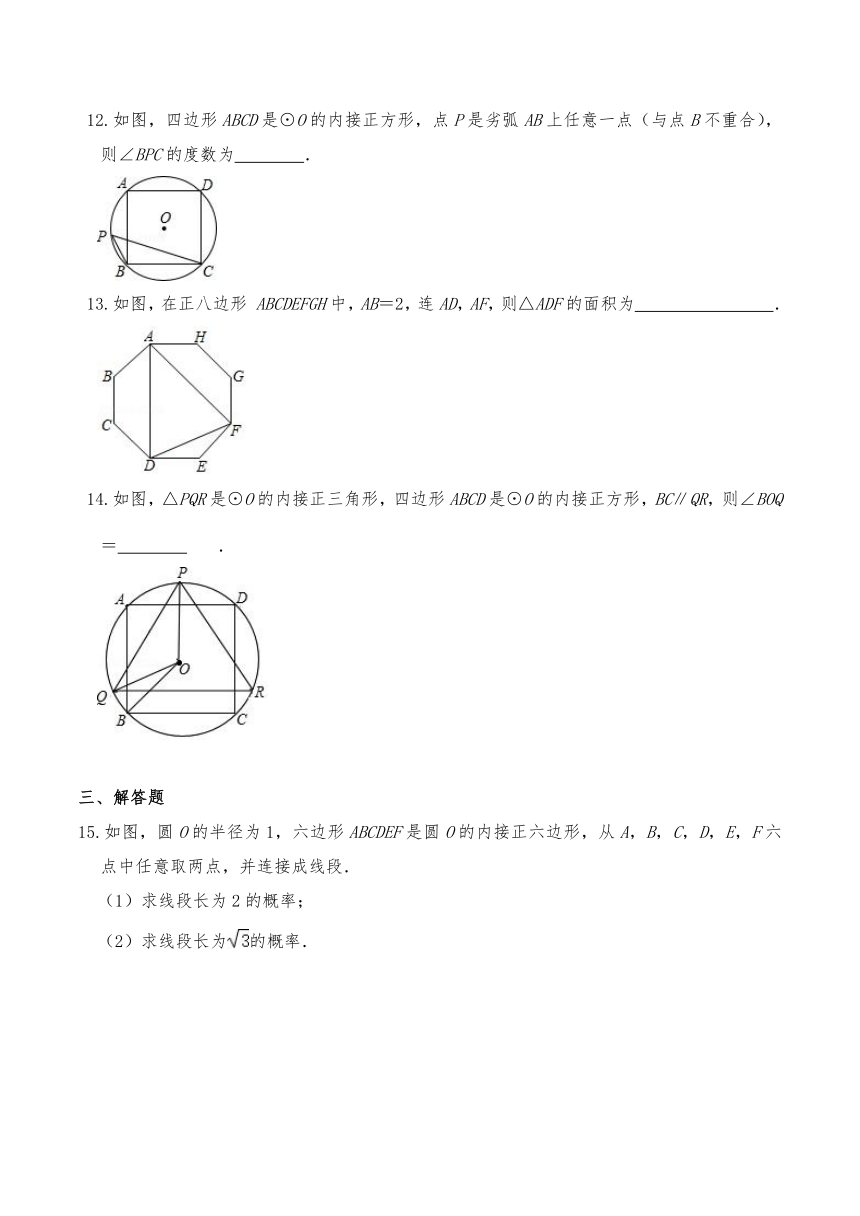
二、填空题
7.如图,在正六边形ABCDEF中,如果向量=,,那么向量用向量,表示为 .
8.⊙O的内接正方形的边长为a和外切正三角形的边长为b,则= .
9.如图,正六边形ABCDEF内接于半径为1的⊙O,则的长为 .
10.如图,点O是正八边形ABCDEFGH的中心点,点M和点N分别在AB和DE上,且AM=DN,则∠MON的大小为 度.
11.如图,正六边形ABCDEF内接于⊙O,点P是直径AD上的一个动点,若⊙O的半径为2cm,则点P到这个正六边形六条边的距离之和为 cm.
12.如图,四边形ABCD是⊙O的内接正方形,点P是劣弧AB上任意一点(与点B不重合),则∠BPC的度数为 .
13.如图,在正八边形 ABCDEFGH中,AB=2,连AD,AF,则△ADF的面积为 .
14.如图,△PQR是⊙O的内接正三角形,四边形ABCD是⊙O的内接正方形,BC∥QR,则∠BOQ= .
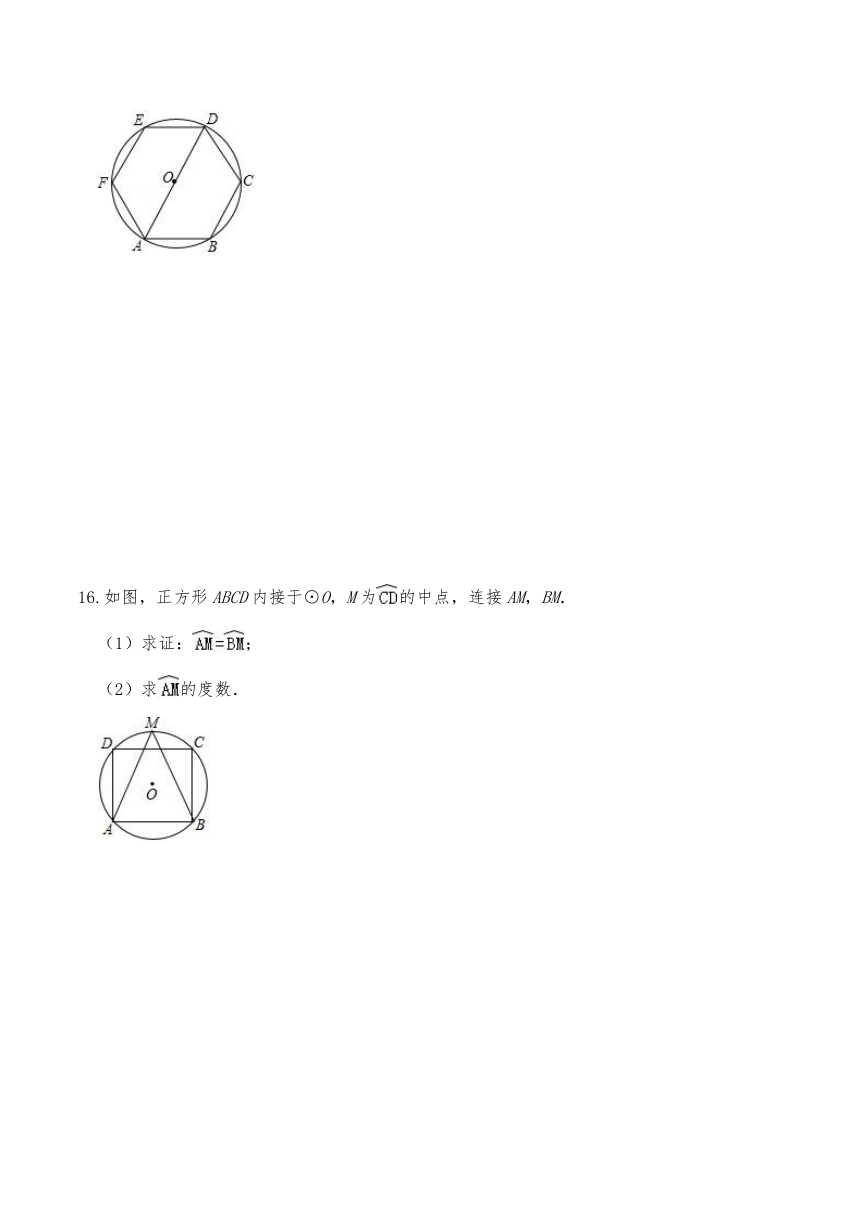
三、解答题
15.如图,圆O的半径为1,六边形ABCDEF是圆O的内接正六边形,从A,B,C,D,E,F六点中任意取两点,并连接成线段.
(1)求线段长为2的概率;
(2)求线段长为的概率.
16.如图,正方形ABCD内接于⊙O,M为的中点,连接AM,BM.
(1)求证:;
(2)求的度数.
17.如图,⊙O外接于正方形ABCD,P为弧AD上一点,且AP=1,PC=3,求正方形ABCD的边长和PB的长.
18.如图,在正五边形ABCDE中,CA与DB相交于点F,若AB=1,求BF.
19.如图,正六边形ABCDEF内接于⊙O,BE是⊙O的直径,连接BF,延长BA,过F作FG⊥BA,垂足为G.
(1)求证:FG是⊙O的切线;
(2)已知FG=2,求图中阴影部分的面积.
20.如图,⊙O半径为4cm,其内接正六边形ABCDEF,点P,Q同时分别从A,D两点出发,以1cm/s速度沿AF,DC向终点F,C运动,连接PB,QE,PE,BQ.设运动时间为t(s).
(1)求证:四边形PEQB为平行四边形;
(2)填空:
①当t= s时,四边形PBQE为菱形;
②当t= s时,四边形PBQE为矩形.
答案
一、选择题
D.D.B.B.B.A.
二、填空题
7.2+2.
8..
9..
10.135.
11.6.
12.45°.
13.4+3.
14.15°.
三、解答题
15.解:(1)连接AE,过点F作FN⊥AE于点N,如图1所示:
∵圆O的半径为1,六边形ABCDEF是圆O的内接正六边形,
∴∠AOB==60°,OA=OB=1,∠AFE=120°,AD=2,
∴△AOB是等边三角形,
∴OA=AB=BC=CD=DE=EF=AE=1,
∴∠FAE=30°,
∴AN=,
∴AE=
同理:AC=,
画树状图如图2所示:
共有30个等可能的结果,线段长为2的结果有6个,
∴线段长为2的概率为=;
(2)由树状图可知,共有30个等可能的结果,线段长为的结果有12个,
∴线段长为的概率为=.
16.(1)证明:∵四边形ABCD是正方形,
∴AD=BC,
∴=,
∵M为的中点,
∴=,
∴+=+,
∴;
(2)解:连接OM,OA,OB,
∵正方形ABCD内接于⊙O,
∴∠AOB=90°,
∴∠AOM=∠BOM=(360°﹣90°)=135°,
∴的度数时135°.
17.解:连接AC,作AE⊥PB于E,如图所示:
∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠ABC=∠D=∠BCD=90°,∠ACB=45°,
∴AC是⊙O的直径,△ABC是等腰直角三角形,
∴∠APC=90°,AC=AB,
∴AC===,
∴AB==,
∵∠APB=∠ACB=45°,AE⊥PB,
∴△APE是等腰直角三角形,
∴PE=AE=AP=,
∴BE===,
∴PB=PE+BE=+.
18.解:在正五边形ABCDE中,∵∠ABC=∠DCB=108°,BC=BA=CD,
∴∠BAC=∠BCA=∠CDB=∠CBD=36°,
∴∠ABF=72°,
∴∠AFB=∠CBD+∠ACB=72°,
∴∠AFB=∠ABF,∠FCB=∠FBC,
∴AF=AB=1,FB=CF,设FB=FC=x,
∵∠BCF=∠BCA,∠CBF=∠CAB,
∴△BCF∽△ACB,
∴CB2=CF CA,
∴x(x+1)=1,
∴x2+x﹣1=0,
∴x=或(舍去),
∴BF=.
19.(1)证明:连接OF,AO,
∵AB=AF=EF,
∴==,
∴∠ABF=∠AFB=∠EBF=30°,
∵OB=OF,
∴∠OBF=∠BFO=30°,
∴∠ABF=∠OFB,
∴AB∥OF,
∵FG⊥BA,
∴OF⊥FG,
∴FG是⊙O的切线;
(2)解:∵==,
∴∠AOF=60°,
∵OA=OF,
∴△AOF是等边三角形,
∴∠AFO=60°,
∴∠AFG=30°,
∵FG=2,
∴AF=4,
∴AO=4,
∵AF∥BE,
∴S△ABF=S△AOF,
∴图中阴影部分的面积==.
20.(1)证明:∵正六边形ABCDEF内接于⊙O,
∴AB=BC=CD=DE=EF=FA,∠A=∠ABC=∠C=∠D=∠DEF=∠F,
∵点P,Q同时分别从A,D两点出发,以1cm/s速度沿AF,DC向终点F,C运动,
∴AP=DQ=t,PF=QC=4﹣t,
在△ABP和△DEQ中,
,
∴△ABP≌△DEQ(SAS),
∴BP=EQ,同理可证PE=QB,
∴四边形PEQB是平行四边形.
(2)解:①当PA=PF,QC=QD时,四边形PBEQ是菱形时,此时t=2s.
②当t=0时,∠EPF=∠PEF=30°,
∴∠BPE=120°﹣30°=90°,
∴此时四边形PBQE是矩形.
当t=4时,同法可知∠BPE=90°,此时四边形PBQE是矩形.
综上所述,t=0s或4s时,四边形PBQE是矩形.
故答案为2s,0s或4s.
一、选择题
1.如果一个正多边形的外角是锐角,且它的余弦值是,那么它是( )
A.等边三角形 B.正六边形 C.正八边形 D.正十二边形
2.在半径为R的圆上依次截取等于R的弦,顺次连接各分点得到的多边形是( )
A.正三角形 B.正四边形 C.正五边形 D.正六边形
3.如图,在正六边形ABCDEF外作正方形DEGH,连接AH,则tan∠HAB等于( )
A.3 B. C.2 D.
4.如图,⊙O的外切正八边形ABCDEFGH的边长2,则⊙O的半径为( )
A.2 B. C.3 D.
5.已知圆的内接正六边形的面积为18,则该圆的半径等于( )
A.3 B.2 C. D.
6.如图,已知⊙O的周长等于6π,则它的内接正六边形ABCDEF的面积是( )
A. B. C. D.
二、填空题
7.如图,在正六边形ABCDEF中,如果向量=,,那么向量用向量,表示为 .
8.⊙O的内接正方形的边长为a和外切正三角形的边长为b,则= .
9.如图,正六边形ABCDEF内接于半径为1的⊙O,则的长为 .
10.如图,点O是正八边形ABCDEFGH的中心点,点M和点N分别在AB和DE上,且AM=DN,则∠MON的大小为 度.
11.如图,正六边形ABCDEF内接于⊙O,点P是直径AD上的一个动点,若⊙O的半径为2cm,则点P到这个正六边形六条边的距离之和为 cm.
12.如图,四边形ABCD是⊙O的内接正方形,点P是劣弧AB上任意一点(与点B不重合),则∠BPC的度数为 .
13.如图,在正八边形 ABCDEFGH中,AB=2,连AD,AF,则△ADF的面积为 .
14.如图,△PQR是⊙O的内接正三角形,四边形ABCD是⊙O的内接正方形,BC∥QR,则∠BOQ= .
三、解答题
15.如图,圆O的半径为1,六边形ABCDEF是圆O的内接正六边形,从A,B,C,D,E,F六点中任意取两点,并连接成线段.
(1)求线段长为2的概率;
(2)求线段长为的概率.
16.如图,正方形ABCD内接于⊙O,M为的中点,连接AM,BM.
(1)求证:;
(2)求的度数.
17.如图,⊙O外接于正方形ABCD,P为弧AD上一点,且AP=1,PC=3,求正方形ABCD的边长和PB的长.
18.如图,在正五边形ABCDE中,CA与DB相交于点F,若AB=1,求BF.
19.如图,正六边形ABCDEF内接于⊙O,BE是⊙O的直径,连接BF,延长BA,过F作FG⊥BA,垂足为G.
(1)求证:FG是⊙O的切线;
(2)已知FG=2,求图中阴影部分的面积.
20.如图,⊙O半径为4cm,其内接正六边形ABCDEF,点P,Q同时分别从A,D两点出发,以1cm/s速度沿AF,DC向终点F,C运动,连接PB,QE,PE,BQ.设运动时间为t(s).
(1)求证:四边形PEQB为平行四边形;
(2)填空:
①当t= s时,四边形PBQE为菱形;
②当t= s时,四边形PBQE为矩形.
答案
一、选择题
D.D.B.B.B.A.
二、填空题
7.2+2.
8..
9..
10.135.
11.6.
12.45°.
13.4+3.
14.15°.
三、解答题
15.解:(1)连接AE,过点F作FN⊥AE于点N,如图1所示:
∵圆O的半径为1,六边形ABCDEF是圆O的内接正六边形,
∴∠AOB==60°,OA=OB=1,∠AFE=120°,AD=2,
∴△AOB是等边三角形,
∴OA=AB=BC=CD=DE=EF=AE=1,
∴∠FAE=30°,
∴AN=,
∴AE=
同理:AC=,
画树状图如图2所示:
共有30个等可能的结果,线段长为2的结果有6个,
∴线段长为2的概率为=;
(2)由树状图可知,共有30个等可能的结果,线段长为的结果有12个,
∴线段长为的概率为=.
16.(1)证明:∵四边形ABCD是正方形,
∴AD=BC,
∴=,
∵M为的中点,
∴=,
∴+=+,
∴;
(2)解:连接OM,OA,OB,
∵正方形ABCD内接于⊙O,
∴∠AOB=90°,
∴∠AOM=∠BOM=(360°﹣90°)=135°,
∴的度数时135°.
17.解:连接AC,作AE⊥PB于E,如图所示:
∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠ABC=∠D=∠BCD=90°,∠ACB=45°,
∴AC是⊙O的直径,△ABC是等腰直角三角形,
∴∠APC=90°,AC=AB,
∴AC===,
∴AB==,
∵∠APB=∠ACB=45°,AE⊥PB,
∴△APE是等腰直角三角形,
∴PE=AE=AP=,
∴BE===,
∴PB=PE+BE=+.
18.解:在正五边形ABCDE中,∵∠ABC=∠DCB=108°,BC=BA=CD,
∴∠BAC=∠BCA=∠CDB=∠CBD=36°,
∴∠ABF=72°,
∴∠AFB=∠CBD+∠ACB=72°,
∴∠AFB=∠ABF,∠FCB=∠FBC,
∴AF=AB=1,FB=CF,设FB=FC=x,
∵∠BCF=∠BCA,∠CBF=∠CAB,
∴△BCF∽△ACB,
∴CB2=CF CA,
∴x(x+1)=1,
∴x2+x﹣1=0,
∴x=或(舍去),
∴BF=.
19.(1)证明:连接OF,AO,
∵AB=AF=EF,
∴==,
∴∠ABF=∠AFB=∠EBF=30°,
∵OB=OF,
∴∠OBF=∠BFO=30°,
∴∠ABF=∠OFB,
∴AB∥OF,
∵FG⊥BA,
∴OF⊥FG,
∴FG是⊙O的切线;
(2)解:∵==,
∴∠AOF=60°,
∵OA=OF,
∴△AOF是等边三角形,
∴∠AFO=60°,
∴∠AFG=30°,
∵FG=2,
∴AF=4,
∴AO=4,
∵AF∥BE,
∴S△ABF=S△AOF,
∴图中阴影部分的面积==.
20.(1)证明:∵正六边形ABCDEF内接于⊙O,
∴AB=BC=CD=DE=EF=FA,∠A=∠ABC=∠C=∠D=∠DEF=∠F,
∵点P,Q同时分别从A,D两点出发,以1cm/s速度沿AF,DC向终点F,C运动,
∴AP=DQ=t,PF=QC=4﹣t,
在△ABP和△DEQ中,
,
∴△ABP≌△DEQ(SAS),
∴BP=EQ,同理可证PE=QB,
∴四边形PEQB是平行四边形.
(2)解:①当PA=PF,QC=QD时,四边形PBEQ是菱形时,此时t=2s.
②当t=0时,∠EPF=∠PEF=30°,
∴∠BPE=120°﹣30°=90°,
∴此时四边形PBQE是矩形.
当t=4时,同法可知∠BPE=90°,此时四边形PBQE是矩形.
综上所述,t=0s或4s时,四边形PBQE是矩形.
故答案为2s,0s或4s.
