沪科版九年级数学下册试题 24.8 综合实践(进球路线与最佳射门角)一课一练(含答案)
文档属性
| 名称 | 沪科版九年级数学下册试题 24.8 综合实践(进球路线与最佳射门角)一课一练(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 220.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-29 16:36:23 | ||
图片预览

文档简介
24.8 综合实践(进球路线与最佳射门角)
一、选择题
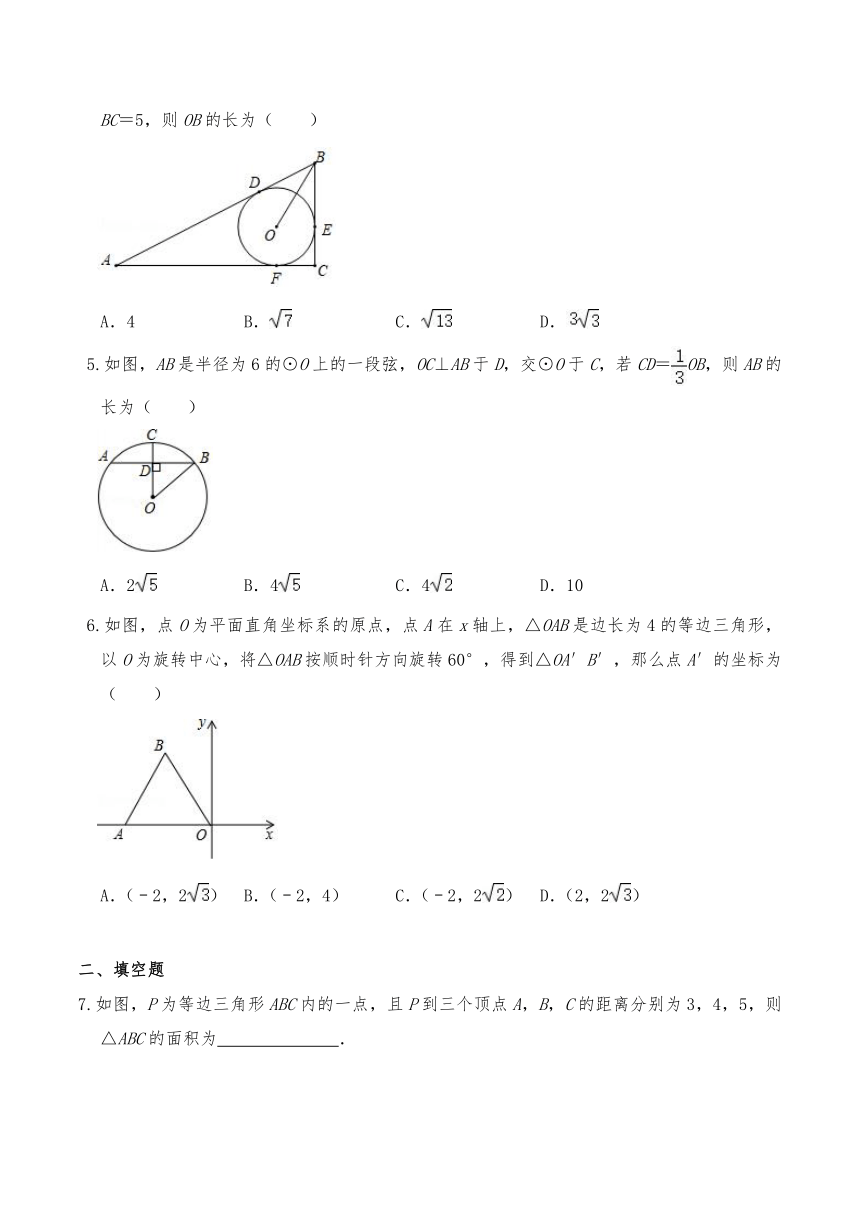
1.用直尺和圆规作∠HDG=∠AOB的过程中,弧②是( )
A.以D为圆心,以DN为半径画弧
B.以M为圆心,以DN长为半径画弧
C.以M为圆心,以EF为半径画弧
D.以D为圆心,以EF长为半径画弧
2.如图,AB是圆O的直径,C、D为圆O上的点,若AC=6,BC=8,若CD平分∠ACB,则CD长为( )
A.10 B.7 C.5 D.7
3.如图,在△ABC中,∠ACB=45°,BC=1,AB=,△AB'C'可以由△ABC绕点A逆时针旋转得到(B与B'对应,C与C'对应),连接CB',且C、B'、C'恰好在同一条直线上,则CC'的长为( )
A.4 B. C. D.3
4.如图,△ABC中,∠ACB=90°,⊙O为△ABC的内切圆,切点分别为D、E、F.若AD=10,BC=5,则OB的长为( )
A.4 B. C. D.
5.如图,AB是半径为6的⊙O上的一段弦,OC⊥AB于D,交⊙O于C,若CD=OB,则AB的长为( )
A.2 B.4 C.4 D.10
6.如图,点O为平面直角坐标系的原点,点A在x轴上,△OAB是边长为4的等边三角形,以O为旋转中心,将△OAB按顺时针方向旋转60°,得到△OA′B′,那么点A′的坐标为( )
A.(﹣2,2) B.(﹣2,4) C.(﹣2,2) D.(2,2)
二、填空题
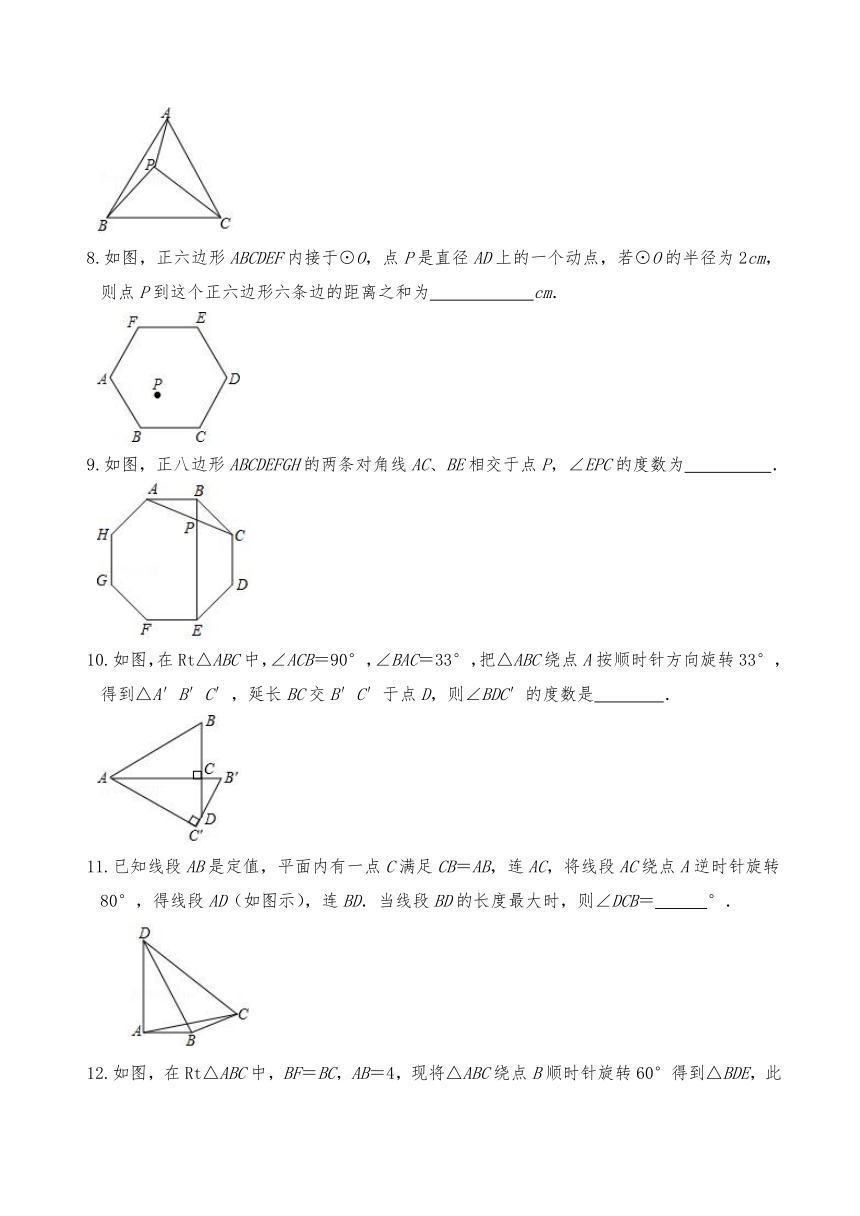
7.如图,P为等边三角形ABC内的一点,且P到三个顶点A,B,C的距离分别为3,4,5,则△ABC的面积为 .
8.如图,正六边形ABCDEF内接于⊙O,点P是直径AD上的一个动点,若⊙O的半径为2cm,则点P到这个正六边形六条边的距离之和为 cm.
9.如图,正八边形ABCDEFGH的两条对角线AC、BE相交于点P,∠EPC的度数为 .
10.如图,在Rt△ABC中,∠ACB=90°,∠BAC=33°,把△ABC绕点A按顺时针方向旋转33°,得到△A′B′C′,延长BC交B′C′于点D,则∠BDC′的度数是 .
11.已知线段AB是定值,平面内有一点C满足CB=AB,连AC,将线段AC绕点A逆时针旋转80°,得线段AD(如图示),连BD.当线段BD的长度最大时,则∠DCB= °.
12.如图,在Rt△ABC中,BF=BC,AB=4,现将△ABC绕点B顺时针旋转60°得到△BDE,此时点B、C、D恰好三点共线,则阴影面积为 ﹣ .
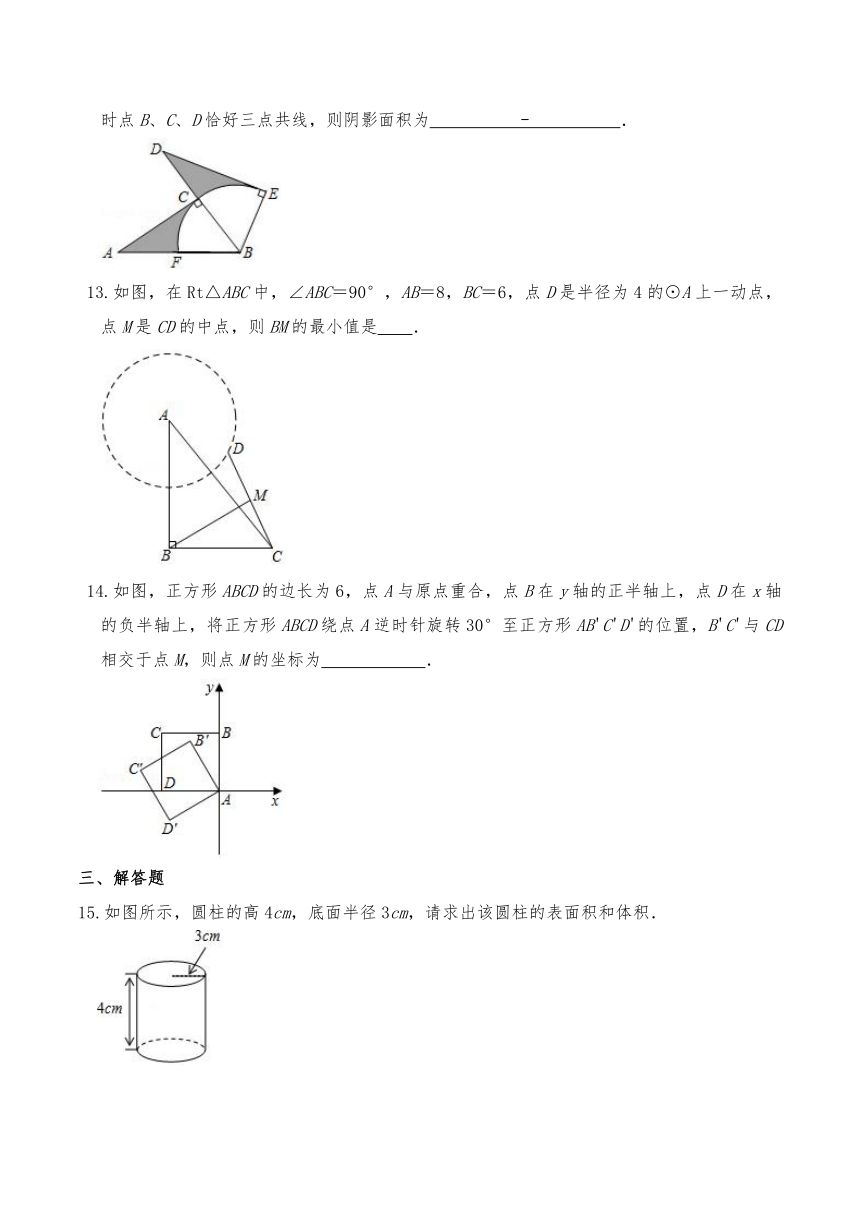
13.如图,在Rt△ABC中,∠ABC=90°,AB=8,BC=6,点D是半径为4的⊙A上一动点,点M是CD的中点,则BM的最小值是 .
14.如图,正方形ABCD的边长为6,点A与原点重合,点B在y轴的正半轴上,点D在x轴的负半轴上,将正方形ABCD绕点A逆时针旋转30°至正方形AB'C'D'的位置,B'C'与CD相交于点M,则点M的坐标为 .
三、解答题
15.如图所示,圆柱的高4cm,底面半径3cm,请求出该圆柱的表面积和体积.
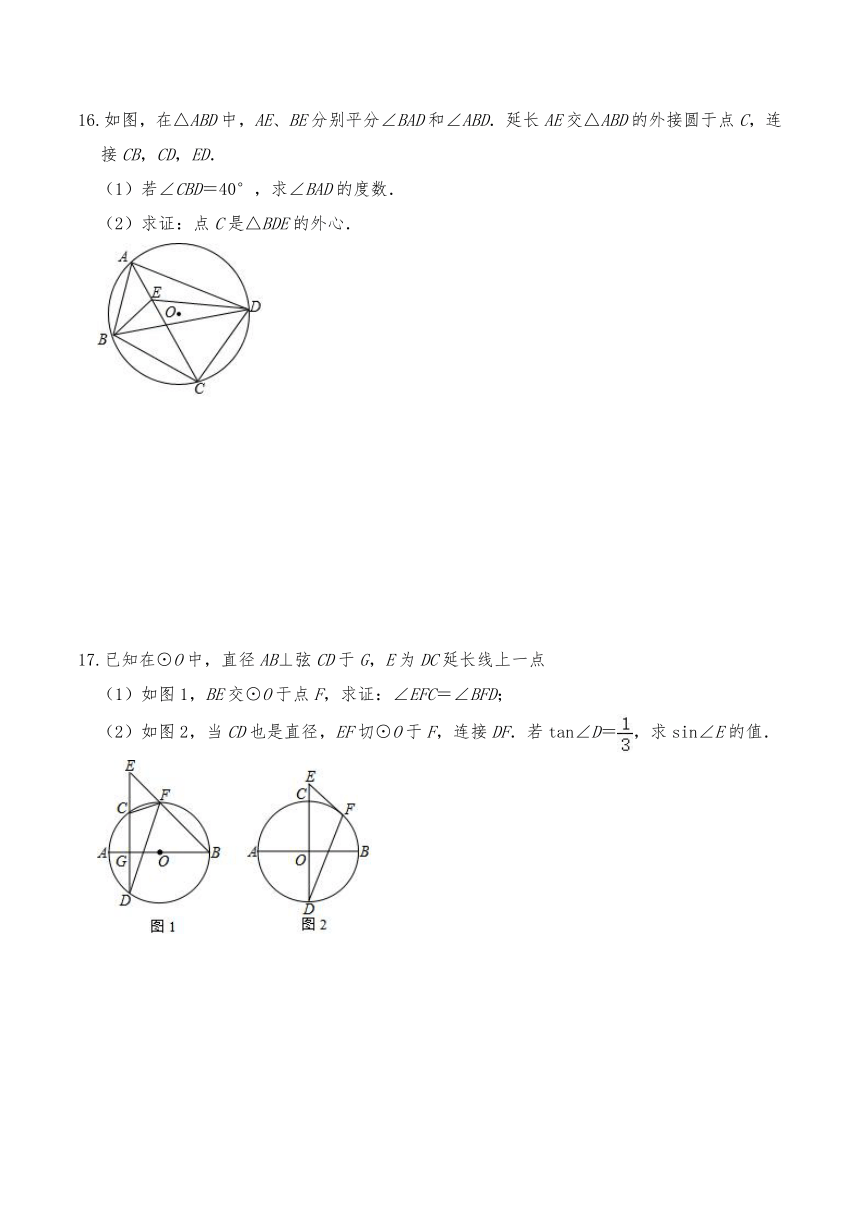
16.如图,在△ABD中,AE、BE分别平分∠BAD和∠ABD.延长AE交△ABD的外接圆于点C,连接CB,CD,ED.
(1)若∠CBD=40°,求∠BAD的度数.
(2)求证:点C是△BDE的外心.
17.已知在⊙O中,直径AB⊥弦CD于G,E为DC延长线上一点
(1)如图1,BE交⊙O于点F,求证:∠EFC=∠BFD;
(2)如图2,当CD也是直径,EF切⊙O于F,连接DF.若tan∠D=,求sin∠E的值.
18.如图,△ABC外切于⊙O,切点分别为D、E、F,BC=7,⊙O的半径为,
(1)∠A=60°,求△ABC的周长.
(2)若∠A=70°,点M为⊙O上异于F、E的动点,则∠FME的度数为 °.
19.如图,四边形ABCO为矩形,点A在x轴上,点C在y轴上,且点B的坐标为(﹣1,2),将此矩形绕点O顺时针旋转90°得矩形DEFO,抛物线y=﹣x2+bx+c过B,E两点.
(1)求此抛物线的函数关系式;
(2)将矩形ABCO向上平移,并且使此抛物线平分线段BC,求平移距离.
20.已知:如图,在Rt△ABC中,∠C=90°,Rt△ABC的内切圆⊙O,切点分别为点D、E、F,
(1)若AC=3,BC=4,求△ABC的内切圆半径;
(2)当AD=5,BD=7时,求△ABC的面积;
(3)当AD=m,BD=n时,直接写出求△ABC的面积(用含m,n的式子表示)为 .
答案
一、选择题
C.D.A.C.B.A.
二、填空题
7. 9+.
8. 6.
9. 67.5°.
10. 147°.
11. 75°.
12. 4﹣.
13. 3.
14.(﹣6,2).
三、解答题
15.解:根据圆柱表面积的计算公式可得π×2×3×4+π×32×2=42π(cm2).
体积π×32×4=36π(cm3)
16.解:(1)∵AE平分∠BAD,
∴∠BAD=2∠CAD,
∵∠CAD=∠CBD=40°,
∴∠BAD=80°;
(2)∵AE、BE分别平分∠BAD和∠ABD,
∴∠BAC=∠DAC,∠ABE=∠DBE,
∴=,
∴BC=CD,
∵∠CBD=∠CAD,
∴∠CBE=∠CBD+∠DBE,∠BEC=∠BAC+∠ABE,
∴∠CBE=∠BEC,
∴BC=EC,
∴BC=EC=DC,
∴点B,E,D在以C为圆心的同一圆上,
∴点C是△BDE的外心.
17.(1)证明:如图1,连接AD,BD,
∵四边形CDBF为圆内接四边形,
∴∠CFE=∠EDB,
∵AB为⊙O的直径,
∴∠ADB=90°,
∴∠DAB+∠ABD=90°,
∵AB⊥CD,
∴∠AGD=90°,
∴∠GDB+∠ABD=90°,
∴∠DAB=∠GDB,
∴∠DAB=∠CFE,
∵∠DAB=∠BFD,
∴∠EFC=∠BFD;
(2)解:如图2,连接OF,CF,
∵EF是⊙O的切线,
∴OF⊥EF,
∴∠EFO=90°,
∵CD是⊙O的直径,
∴∠CFD=90°,
∴∠EFC=∠OFD,
∵OF=OD,
∴∠ODF=∠OFD,
∴∠ODF=∠EFC,
∵∠CEF=∠FED,
∴△CEF∽△FED,
∴,
∴EF2=CE DE,
∵tan∠D==,
设CF=a,则DF=3a,由勾股定理可得CD=,
设CE=x,则EF=3x,
∴,
解得:x=,
∴,
∴OE=CE+OC=,
∴==,
∴sin∠E=.
18.解:(1)连接OE、OF、OA,如图,
∵△ABC外切于⊙O,切点分别为D、E、F,
∴BD=BF,CD=CE,OE⊥AC,OF⊥AB,OA平分∠BAC,
∴∠OAE=×60°=30°,
∴AE=OE=×=3,
∴△ABC的周长=BC+BF+AF+AE+CE=BC+BD+CD+2AE=2BC+2AE=2×7+2×3=1=20;
(2)∵OE⊥AC,OF⊥AB,
∴∠OEA=∠OFA=90°,
∴∠EOF=180°﹣∠BAC=180°﹣70°=110°,
当点M在上时,如图,∠FME=∠EOF=55°;
当点M在上时,如图,∠FM′E=180°﹣55°=125°,
综上所述,∠FME的度数为55°或125°.
故答案为55或125.
19.解:(1)由旋转的性质得:E(2,1),
把B(﹣1,2),E(2,1)代入y=﹣x2+bx+c得,
,解得:b=,c=,
∴抛物线的函数关系式为y=﹣x2+x+;
(2)当x=﹣时,y=﹣+×(﹣)+=,
∴平移的距离为:﹣2=,
答:平移的距离为.
20.解:(1)连接OD、OE、OF,如图,设⊙O的半径为r,
在Rt△ABC中,AB==5,
∵Rt△ABC的内切圆⊙O,切点分别为点D、E、F,
∴OE⊥AC,OF⊥BC,CE=CF,AE=AD,BF=BD,
易得四边形CFOE为正方形,
∴CE=CF=OE=r,
∴AD=AE=3﹣r,BD=BF=4﹣r,
∴3﹣r+4﹣r=5,解得r=1,
即△ABC的内切圆半径为1;
(2)设⊙O的半径为r,
由(1)得AE=AD=5,BF=BD=7,
∴AC=5+r,BC=7+r,
在Rt△ABC中,(5+r)2+(7+r)2=(5+7)2,解得r=﹣6或r=﹣﹣6(舍去),
∴AC=﹣6+5=﹣1,BC=﹣6+7=+1,
∴S△ABC=(﹣1)(+1)=35;
(3)设⊙O的半径为r,
由(1)得AE=AD=m,BF=BD=n,
∴AC=m+r,BC=n+r,
在Rt△ABC中,(m+r)2+(n+r)2=(m+n)2,解得r=或r=(舍去),
∴AC=(m﹣n+),BC=(﹣m+n+),
∴S△ABC=×=(m﹣n+)×(﹣m+n+)=[)2﹣(m﹣n)2]=mn.
故答案为mn.
一、选择题
1.用直尺和圆规作∠HDG=∠AOB的过程中,弧②是( )
A.以D为圆心,以DN为半径画弧
B.以M为圆心,以DN长为半径画弧
C.以M为圆心,以EF为半径画弧
D.以D为圆心,以EF长为半径画弧
2.如图,AB是圆O的直径,C、D为圆O上的点,若AC=6,BC=8,若CD平分∠ACB,则CD长为( )
A.10 B.7 C.5 D.7
3.如图,在△ABC中,∠ACB=45°,BC=1,AB=,△AB'C'可以由△ABC绕点A逆时针旋转得到(B与B'对应,C与C'对应),连接CB',且C、B'、C'恰好在同一条直线上,则CC'的长为( )
A.4 B. C. D.3
4.如图,△ABC中,∠ACB=90°,⊙O为△ABC的内切圆,切点分别为D、E、F.若AD=10,BC=5,则OB的长为( )
A.4 B. C. D.
5.如图,AB是半径为6的⊙O上的一段弦,OC⊥AB于D,交⊙O于C,若CD=OB,则AB的长为( )
A.2 B.4 C.4 D.10
6.如图,点O为平面直角坐标系的原点,点A在x轴上,△OAB是边长为4的等边三角形,以O为旋转中心,将△OAB按顺时针方向旋转60°,得到△OA′B′,那么点A′的坐标为( )
A.(﹣2,2) B.(﹣2,4) C.(﹣2,2) D.(2,2)
二、填空题
7.如图,P为等边三角形ABC内的一点,且P到三个顶点A,B,C的距离分别为3,4,5,则△ABC的面积为 .
8.如图,正六边形ABCDEF内接于⊙O,点P是直径AD上的一个动点,若⊙O的半径为2cm,则点P到这个正六边形六条边的距离之和为 cm.
9.如图,正八边形ABCDEFGH的两条对角线AC、BE相交于点P,∠EPC的度数为 .
10.如图,在Rt△ABC中,∠ACB=90°,∠BAC=33°,把△ABC绕点A按顺时针方向旋转33°,得到△A′B′C′,延长BC交B′C′于点D,则∠BDC′的度数是 .
11.已知线段AB是定值,平面内有一点C满足CB=AB,连AC,将线段AC绕点A逆时针旋转80°,得线段AD(如图示),连BD.当线段BD的长度最大时,则∠DCB= °.
12.如图,在Rt△ABC中,BF=BC,AB=4,现将△ABC绕点B顺时针旋转60°得到△BDE,此时点B、C、D恰好三点共线,则阴影面积为 ﹣ .
13.如图,在Rt△ABC中,∠ABC=90°,AB=8,BC=6,点D是半径为4的⊙A上一动点,点M是CD的中点,则BM的最小值是 .
14.如图,正方形ABCD的边长为6,点A与原点重合,点B在y轴的正半轴上,点D在x轴的负半轴上,将正方形ABCD绕点A逆时针旋转30°至正方形AB'C'D'的位置,B'C'与CD相交于点M,则点M的坐标为 .
三、解答题
15.如图所示,圆柱的高4cm,底面半径3cm,请求出该圆柱的表面积和体积.
16.如图,在△ABD中,AE、BE分别平分∠BAD和∠ABD.延长AE交△ABD的外接圆于点C,连接CB,CD,ED.
(1)若∠CBD=40°,求∠BAD的度数.
(2)求证:点C是△BDE的外心.
17.已知在⊙O中,直径AB⊥弦CD于G,E为DC延长线上一点
(1)如图1,BE交⊙O于点F,求证:∠EFC=∠BFD;
(2)如图2,当CD也是直径,EF切⊙O于F,连接DF.若tan∠D=,求sin∠E的值.
18.如图,△ABC外切于⊙O,切点分别为D、E、F,BC=7,⊙O的半径为,
(1)∠A=60°,求△ABC的周长.
(2)若∠A=70°,点M为⊙O上异于F、E的动点,则∠FME的度数为 °.
19.如图,四边形ABCO为矩形,点A在x轴上,点C在y轴上,且点B的坐标为(﹣1,2),将此矩形绕点O顺时针旋转90°得矩形DEFO,抛物线y=﹣x2+bx+c过B,E两点.
(1)求此抛物线的函数关系式;
(2)将矩形ABCO向上平移,并且使此抛物线平分线段BC,求平移距离.
20.已知:如图,在Rt△ABC中,∠C=90°,Rt△ABC的内切圆⊙O,切点分别为点D、E、F,
(1)若AC=3,BC=4,求△ABC的内切圆半径;
(2)当AD=5,BD=7时,求△ABC的面积;
(3)当AD=m,BD=n时,直接写出求△ABC的面积(用含m,n的式子表示)为 .
答案
一、选择题
C.D.A.C.B.A.
二、填空题
7. 9+.
8. 6.
9. 67.5°.
10. 147°.
11. 75°.
12. 4﹣.
13. 3.
14.(﹣6,2).
三、解答题
15.解:根据圆柱表面积的计算公式可得π×2×3×4+π×32×2=42π(cm2).
体积π×32×4=36π(cm3)
16.解:(1)∵AE平分∠BAD,
∴∠BAD=2∠CAD,
∵∠CAD=∠CBD=40°,
∴∠BAD=80°;
(2)∵AE、BE分别平分∠BAD和∠ABD,
∴∠BAC=∠DAC,∠ABE=∠DBE,
∴=,
∴BC=CD,
∵∠CBD=∠CAD,
∴∠CBE=∠CBD+∠DBE,∠BEC=∠BAC+∠ABE,
∴∠CBE=∠BEC,
∴BC=EC,
∴BC=EC=DC,
∴点B,E,D在以C为圆心的同一圆上,
∴点C是△BDE的外心.
17.(1)证明:如图1,连接AD,BD,
∵四边形CDBF为圆内接四边形,
∴∠CFE=∠EDB,
∵AB为⊙O的直径,
∴∠ADB=90°,
∴∠DAB+∠ABD=90°,
∵AB⊥CD,
∴∠AGD=90°,
∴∠GDB+∠ABD=90°,
∴∠DAB=∠GDB,
∴∠DAB=∠CFE,
∵∠DAB=∠BFD,
∴∠EFC=∠BFD;
(2)解:如图2,连接OF,CF,
∵EF是⊙O的切线,
∴OF⊥EF,
∴∠EFO=90°,
∵CD是⊙O的直径,
∴∠CFD=90°,
∴∠EFC=∠OFD,
∵OF=OD,
∴∠ODF=∠OFD,
∴∠ODF=∠EFC,
∵∠CEF=∠FED,
∴△CEF∽△FED,
∴,
∴EF2=CE DE,
∵tan∠D==,
设CF=a,则DF=3a,由勾股定理可得CD=,
设CE=x,则EF=3x,
∴,
解得:x=,
∴,
∴OE=CE+OC=,
∴==,
∴sin∠E=.
18.解:(1)连接OE、OF、OA,如图,
∵△ABC外切于⊙O,切点分别为D、E、F,
∴BD=BF,CD=CE,OE⊥AC,OF⊥AB,OA平分∠BAC,
∴∠OAE=×60°=30°,
∴AE=OE=×=3,
∴△ABC的周长=BC+BF+AF+AE+CE=BC+BD+CD+2AE=2BC+2AE=2×7+2×3=1=20;
(2)∵OE⊥AC,OF⊥AB,
∴∠OEA=∠OFA=90°,
∴∠EOF=180°﹣∠BAC=180°﹣70°=110°,
当点M在上时,如图,∠FME=∠EOF=55°;
当点M在上时,如图,∠FM′E=180°﹣55°=125°,
综上所述,∠FME的度数为55°或125°.
故答案为55或125.
19.解:(1)由旋转的性质得:E(2,1),
把B(﹣1,2),E(2,1)代入y=﹣x2+bx+c得,
,解得:b=,c=,
∴抛物线的函数关系式为y=﹣x2+x+;
(2)当x=﹣时,y=﹣+×(﹣)+=,
∴平移的距离为:﹣2=,
答:平移的距离为.
20.解:(1)连接OD、OE、OF,如图,设⊙O的半径为r,
在Rt△ABC中,AB==5,
∵Rt△ABC的内切圆⊙O,切点分别为点D、E、F,
∴OE⊥AC,OF⊥BC,CE=CF,AE=AD,BF=BD,
易得四边形CFOE为正方形,
∴CE=CF=OE=r,
∴AD=AE=3﹣r,BD=BF=4﹣r,
∴3﹣r+4﹣r=5,解得r=1,
即△ABC的内切圆半径为1;
(2)设⊙O的半径为r,
由(1)得AE=AD=5,BF=BD=7,
∴AC=5+r,BC=7+r,
在Rt△ABC中,(5+r)2+(7+r)2=(5+7)2,解得r=﹣6或r=﹣﹣6(舍去),
∴AC=﹣6+5=﹣1,BC=﹣6+7=+1,
∴S△ABC=(﹣1)(+1)=35;
(3)设⊙O的半径为r,
由(1)得AE=AD=m,BF=BD=n,
∴AC=m+r,BC=n+r,
在Rt△ABC中,(m+r)2+(n+r)2=(m+n)2,解得r=或r=(舍去),
∴AC=(m﹣n+),BC=(﹣m+n+),
∴S△ABC=×=(m﹣n+)×(﹣m+n+)=[)2﹣(m﹣n)2]=mn.
故答案为mn.
