沪科版九年级数学下册试题 25.1投影 一课一练(含答案)
文档属性
| 名称 | 沪科版九年级数学下册试题 25.1投影 一课一练(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 222.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-29 00:00:00 | ||
图片预览



文档简介
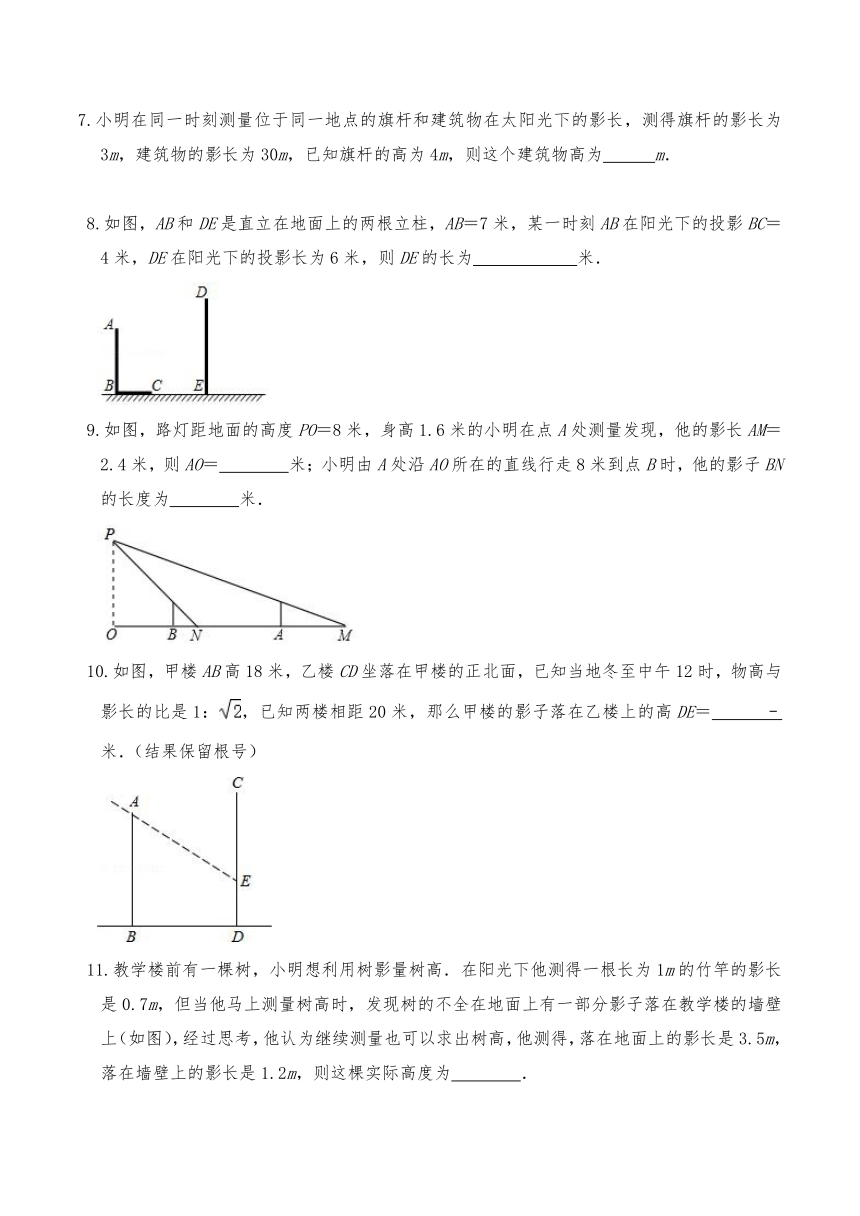
25.1投影
一、选择题
1.圆形的纸片在平行投影下的正投影是( )
A.圆形 B.椭圆形 C.线段 D.以上都可能
2.如图是一棵小树一天内在太阳下不同时刻的照片,将它们按时间先后顺序进行排列正确的是( )
③﹣④﹣①﹣② B.②﹣①﹣④﹣③
C.④﹣①﹣②﹣③ D.④﹣①﹣③﹣②
3.数学兴趣小组的同学们想利用树影测量树高.课外活动时他们在阳光下测得一根长为1米的竹竿的影子是0.9米,同一时刻测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的台阶上,且影子的末端刚好落在最后一级台阶的上端C处,他们测得落在地面的影长为1.1米,台阶总的高度为1.0米,台阶水平总宽度为1.6米.则树高为( )
A.3.0m B.4.0m C.5.0m D.6.0m
4.如图,有一高度为8m的灯塔AB,在灯光下,身高为1.6m的小亮从距离灯塔底端4.8m的点C处,沿BC方向前进3.2m到达点D处,那么他的影长( )
A.变长了0.8m B.变长了1.2m C.变短了0.8m D.变短了1.2m
5.如图,一人站在两等高的路灯之间走动,GB为人AB在路灯EF照射下的影子,BH为人AB在路灯CD照射下的影子.当人从点C走向点E时两段影子之和GH的变化趋势是( )
A.先变长后变短 B.先变短后变长
C.不变 D.先变短后变长再变短
6.山重水复的地形景观造就了网红重庆,南山的一棵树观景台更是外地游客打卡的必去之地.如图,山坡AB的坡度为1:2.4,坡上有一棵树BC,当太阳光线与水平线成68°沿斜坡照下时,在斜坡上的树影AB长为13米,则这棵树BC高度为( )米.(结果保留一位小数,参考数据:sin68°≈0.93,cos68°≈0.38,tan68°≈2.48)
A.29.7 B.29.8 C.24.8 D.24.7
二、填空题
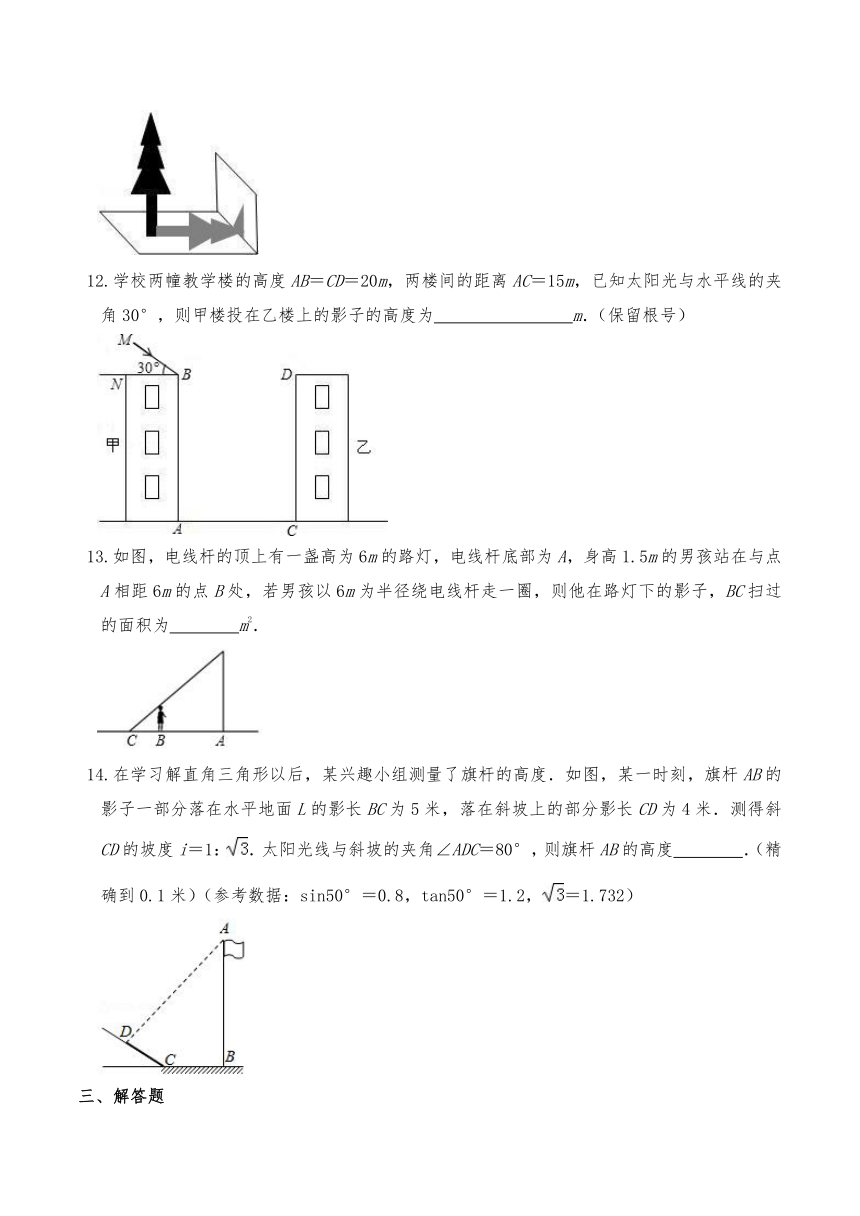
7.小明在同一时刻测量位于同一地点的旗杆和建筑物在太阳光下的影长,测得旗杆的影长为3m,建筑物的影长为30m,已知旗杆的高为4m,则这个建筑物高为 m.
8.如图,AB和DE是直立在地面上的两根立柱,AB=7米,某一时刻AB在阳光下的投影BC=4米,DE在阳光下的投影长为6米,则DE的长为 米.
9.如图,路灯距地面的高度PO=8米,身高1.6米的小明在点A处测量发现,他的影长AM=2.4米,则AO= 米;小明由A处沿AO所在的直线行走8米到点B时,他的影子BN的长度为 米.
10.如图,甲楼AB高18米,乙楼CD坐落在甲楼的正北面,已知当地冬至中午12时,物高与影长的比是1:,已知两楼相距20米,那么甲楼的影子落在乙楼上的高DE= ﹣ 米.(结果保留根号)
11.教学楼前有一棵树,小明想利用树影量树高.在阳光下他测得一根长为1m的竹竿的影长是0.7m,但当他马上测量树高时,发现树的不全在地面上有一部分影子落在教学楼的墙壁上(如图),经过思考,他认为继续测量也可以求出树高,他测得,落在地面上的影长是3.5m,落在墙壁上的影长是1.2m,则这棵实际高度为 .
12.学校两幢教学楼的高度AB=CD=20m,两楼间的距离AC=15m,已知太阳光与水平线的夹角30°,则甲楼投在乙楼上的影子的高度为 m.(保留根号)
13.如图,电线杆的顶上有一盏高为6m的路灯,电线杆底部为A,身高1.5m的男孩站在与点A相距6m的点B处,若男孩以6m为半径绕电线杆走一圈,则他在路灯下的影子,BC扫过的面积为 m2.
14.在学习解直角三角形以后,某兴趣小组测量了旗杆的高度.如图,某一时刻,旗杆AB的影子一部分落在水平地面L的影长BC为5米,落在斜坡上的部分影长CD为4米.测得斜CD的坡度i=1:.太阳光线与斜坡的夹角∠ADC=80°,则旗杆AB的高度 .(精确到0.1米)(参考数据:sin50°=0.8,tan50°=1.2,=1.732)
三、解答题
15.小明开着汽车在平坦的公路上行驶,前放出现两座建筑物A、B(如图),在(1)处小颖能看到B建筑物的一部分,(如图),此时,小明的视角为30°,已知A建筑物高25米.
(1)请问汽车行驶到什么位置时,小明刚好看不到建筑物B?请在图中标出这点.
(2)若小明刚好看不到B建筑物时,他的视线与公路的夹角为45°,请问他向前行驶了多少米?( 精确到0.1)
16.如图,小明晚上由路灯A下的点B处走到点C处时,测得自身影子CD的长为1米,他继续往前走3米到达点E处(即CE=3米),测得自己影子EF的长为2米,已知小明的身高是1.5米,求路灯AB的高度.
17.如图,学校操场旁立着一杆路灯(线段OP).小明拿着一根长2m的竹竿去测量路灯的高度,他走到路灯旁的一个地点A竖起竹竿(线段AE),这时他量了一下竹竿的影长AC正好是1m,他沿着影子的方向走了4m到达点B,又竖起竹竿(线段BF),这时竹竿的影长BD正好是2m,请利用上述条件求出路灯的高度.
18.如图,小明想测量电线杆AB的高度,但在太阳光下,电线杆的影子恰好落在地面和土坡的坡面上,量得坡面上的影长CD=4m,地面上的影长BC=10m,土坡坡面与地面成30°的角,此时测得1m长的木杆的影长为2m,求电线杆的高度.(结果保留根号)
19.如图,一位同学想利用树影测量树高(AB),他在某一时刻测得高为1m的竹竿影长为0.9m,但当他马上测量树影时,因树靠近一幢建筑物,影子不全落在地面上,有一部分影子在墙上(CD),他先测得留在墙上的影高(CD)为1.2m,又测得地面部分的影长(BC)为2.7m,他测得的树高应为多少米?
20.实践活动小组要测量旗杆的高度,现有标杆、皮尺.小明同学站在旗杆一侧,通过观测和其他同学的测量,求出了旗杆的高度.请完成下列问题:
(1)小明的站点D,旗杆的接地点B,标杆的接地点F,三点应满足什么关系?
(2)在测量过程中,如果标杆的位置确定,小明应该通过移动位置,直到小明的视点C与点 在同一直线上为止;
(3)他们都测得了哪些数据就能计算出旗杆的高度?请你用小写字母表示这些数据(不允许测量多余的数据);
(4)请用(3)中的数据,直接表示出旗杆的高度.
答案
一、选择题
D.B.B.A.C.C.
二、填空题
7.40.
8..
9. 9.6,6.4.
10.(18﹣10)
11.6.2m
12.(20﹣5)
13.28π.
14.12.2m.
三、解答题
15.解:(1)如图所示:
汽车行驶到E点位置时,小明刚好看不到建筑物B;
(2)∵小明的视角为30°,A建筑物高25米,
∴AC=25,
tan30°==,
∴AM=25,
∵∠AEC=45°,
∴AE=AC=25m,
∴ME=AM﹣AE=43.3﹣25=18.3m.
则他向前行驶了18.3米.
16.解:∵MC∥AB,
∴△DCM∽△DAB,
∴=,即=①,
∵NE∥AB,
∴△FNE∽△FAB,
∴=,即=②,
∴=,
解得BC=3,
∴=,
解得AB=6,
答:路灯A的高度AB为6m.
17.解:由于BF=DB=2m,即∠D=45°,
∴DP=OP=灯高.
在△CEA与△COP中,
∵AE⊥CP,OP⊥CP,
∴AE∥OP.
∴△CEA∽△COP,
∴.
设AP=xm,OP=hm,则,①,
DP=OP=2+4+x=h,②
联立①②两式,
解得x=4,h=10.
∴路灯有10m高.
18.解解:如图,过D作DE⊥BC的延长线于E,连接AD并延长交BC的延长线于F,
∵CD=4米,CD与地面成30°角,
∴DE=CD=×4=2米,根据勾股定理得,CE=米,
∵1米杆的影长为2米,
∴,
∴EF=2DE=2×2=4米,
∴BF=BC+CE+EF=10+2+4=(14+2)米,
∵,
∴AB=(14+2)=(7+)米.
答:电线杆的高度为(7+)m.
19.解:设墙上的影高CD落在地面上时的长度为xm,树高为hm,
∵某一时刻测得长为1m的竹竿影长为0.9m,墙上的影高CD为1.2m,
∴,解得x=1.08(m),
∴树的影长为:1.08+2.7=3.78(m),
∴,解得h=4.2(m).
答:测得的树高为4.2米.
20.解:(1)小明的站点D,旗杆的接地点B,标杆的接地点F,三点应在同一直线上.
(2)在测量过程中,如果标杆的位置确定,小明应该通过移动位置,直到小明的视点C,点E和点A在同一直线上为止.
故答案为:E和点A.
(3)答案不唯一.测量CD,EF,DF,FB即可.设测量得到CD=a,EF=b,DF=c,FB=d.
(4)作CH⊥AB于H,交EF于K.则四边形CDBH,四边形CDFK是矩形,
∴CK=DF=c,BF=KH=d,CD=FK=BH=a,EK=b﹣a.
∵EK∥AH,
∴△CKE∽△CHB,
∴=,
∴=,
∴AH=,
∴AB=AH+HB=+a=.
一、选择题
1.圆形的纸片在平行投影下的正投影是( )
A.圆形 B.椭圆形 C.线段 D.以上都可能
2.如图是一棵小树一天内在太阳下不同时刻的照片,将它们按时间先后顺序进行排列正确的是( )
③﹣④﹣①﹣② B.②﹣①﹣④﹣③
C.④﹣①﹣②﹣③ D.④﹣①﹣③﹣②
3.数学兴趣小组的同学们想利用树影测量树高.课外活动时他们在阳光下测得一根长为1米的竹竿的影子是0.9米,同一时刻测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的台阶上,且影子的末端刚好落在最后一级台阶的上端C处,他们测得落在地面的影长为1.1米,台阶总的高度为1.0米,台阶水平总宽度为1.6米.则树高为( )
A.3.0m B.4.0m C.5.0m D.6.0m
4.如图,有一高度为8m的灯塔AB,在灯光下,身高为1.6m的小亮从距离灯塔底端4.8m的点C处,沿BC方向前进3.2m到达点D处,那么他的影长( )
A.变长了0.8m B.变长了1.2m C.变短了0.8m D.变短了1.2m
5.如图,一人站在两等高的路灯之间走动,GB为人AB在路灯EF照射下的影子,BH为人AB在路灯CD照射下的影子.当人从点C走向点E时两段影子之和GH的变化趋势是( )
A.先变长后变短 B.先变短后变长
C.不变 D.先变短后变长再变短
6.山重水复的地形景观造就了网红重庆,南山的一棵树观景台更是外地游客打卡的必去之地.如图,山坡AB的坡度为1:2.4,坡上有一棵树BC,当太阳光线与水平线成68°沿斜坡照下时,在斜坡上的树影AB长为13米,则这棵树BC高度为( )米.(结果保留一位小数,参考数据:sin68°≈0.93,cos68°≈0.38,tan68°≈2.48)
A.29.7 B.29.8 C.24.8 D.24.7
二、填空题
7.小明在同一时刻测量位于同一地点的旗杆和建筑物在太阳光下的影长,测得旗杆的影长为3m,建筑物的影长为30m,已知旗杆的高为4m,则这个建筑物高为 m.
8.如图,AB和DE是直立在地面上的两根立柱,AB=7米,某一时刻AB在阳光下的投影BC=4米,DE在阳光下的投影长为6米,则DE的长为 米.
9.如图,路灯距地面的高度PO=8米,身高1.6米的小明在点A处测量发现,他的影长AM=2.4米,则AO= 米;小明由A处沿AO所在的直线行走8米到点B时,他的影子BN的长度为 米.
10.如图,甲楼AB高18米,乙楼CD坐落在甲楼的正北面,已知当地冬至中午12时,物高与影长的比是1:,已知两楼相距20米,那么甲楼的影子落在乙楼上的高DE= ﹣ 米.(结果保留根号)
11.教学楼前有一棵树,小明想利用树影量树高.在阳光下他测得一根长为1m的竹竿的影长是0.7m,但当他马上测量树高时,发现树的不全在地面上有一部分影子落在教学楼的墙壁上(如图),经过思考,他认为继续测量也可以求出树高,他测得,落在地面上的影长是3.5m,落在墙壁上的影长是1.2m,则这棵实际高度为 .
12.学校两幢教学楼的高度AB=CD=20m,两楼间的距离AC=15m,已知太阳光与水平线的夹角30°,则甲楼投在乙楼上的影子的高度为 m.(保留根号)
13.如图,电线杆的顶上有一盏高为6m的路灯,电线杆底部为A,身高1.5m的男孩站在与点A相距6m的点B处,若男孩以6m为半径绕电线杆走一圈,则他在路灯下的影子,BC扫过的面积为 m2.
14.在学习解直角三角形以后,某兴趣小组测量了旗杆的高度.如图,某一时刻,旗杆AB的影子一部分落在水平地面L的影长BC为5米,落在斜坡上的部分影长CD为4米.测得斜CD的坡度i=1:.太阳光线与斜坡的夹角∠ADC=80°,则旗杆AB的高度 .(精确到0.1米)(参考数据:sin50°=0.8,tan50°=1.2,=1.732)
三、解答题
15.小明开着汽车在平坦的公路上行驶,前放出现两座建筑物A、B(如图),在(1)处小颖能看到B建筑物的一部分,(如图),此时,小明的视角为30°,已知A建筑物高25米.
(1)请问汽车行驶到什么位置时,小明刚好看不到建筑物B?请在图中标出这点.
(2)若小明刚好看不到B建筑物时,他的视线与公路的夹角为45°,请问他向前行驶了多少米?( 精确到0.1)
16.如图,小明晚上由路灯A下的点B处走到点C处时,测得自身影子CD的长为1米,他继续往前走3米到达点E处(即CE=3米),测得自己影子EF的长为2米,已知小明的身高是1.5米,求路灯AB的高度.
17.如图,学校操场旁立着一杆路灯(线段OP).小明拿着一根长2m的竹竿去测量路灯的高度,他走到路灯旁的一个地点A竖起竹竿(线段AE),这时他量了一下竹竿的影长AC正好是1m,他沿着影子的方向走了4m到达点B,又竖起竹竿(线段BF),这时竹竿的影长BD正好是2m,请利用上述条件求出路灯的高度.
18.如图,小明想测量电线杆AB的高度,但在太阳光下,电线杆的影子恰好落在地面和土坡的坡面上,量得坡面上的影长CD=4m,地面上的影长BC=10m,土坡坡面与地面成30°的角,此时测得1m长的木杆的影长为2m,求电线杆的高度.(结果保留根号)
19.如图,一位同学想利用树影测量树高(AB),他在某一时刻测得高为1m的竹竿影长为0.9m,但当他马上测量树影时,因树靠近一幢建筑物,影子不全落在地面上,有一部分影子在墙上(CD),他先测得留在墙上的影高(CD)为1.2m,又测得地面部分的影长(BC)为2.7m,他测得的树高应为多少米?
20.实践活动小组要测量旗杆的高度,现有标杆、皮尺.小明同学站在旗杆一侧,通过观测和其他同学的测量,求出了旗杆的高度.请完成下列问题:
(1)小明的站点D,旗杆的接地点B,标杆的接地点F,三点应满足什么关系?
(2)在测量过程中,如果标杆的位置确定,小明应该通过移动位置,直到小明的视点C与点 在同一直线上为止;
(3)他们都测得了哪些数据就能计算出旗杆的高度?请你用小写字母表示这些数据(不允许测量多余的数据);
(4)请用(3)中的数据,直接表示出旗杆的高度.
答案
一、选择题
D.B.B.A.C.C.
二、填空题
7.40.
8..
9. 9.6,6.4.
10.(18﹣10)
11.6.2m
12.(20﹣5)
13.28π.
14.12.2m.
三、解答题
15.解:(1)如图所示:
汽车行驶到E点位置时,小明刚好看不到建筑物B;
(2)∵小明的视角为30°,A建筑物高25米,
∴AC=25,
tan30°==,
∴AM=25,
∵∠AEC=45°,
∴AE=AC=25m,
∴ME=AM﹣AE=43.3﹣25=18.3m.
则他向前行驶了18.3米.
16.解:∵MC∥AB,
∴△DCM∽△DAB,
∴=,即=①,
∵NE∥AB,
∴△FNE∽△FAB,
∴=,即=②,
∴=,
解得BC=3,
∴=,
解得AB=6,
答:路灯A的高度AB为6m.
17.解:由于BF=DB=2m,即∠D=45°,
∴DP=OP=灯高.
在△CEA与△COP中,
∵AE⊥CP,OP⊥CP,
∴AE∥OP.
∴△CEA∽△COP,
∴.
设AP=xm,OP=hm,则,①,
DP=OP=2+4+x=h,②
联立①②两式,
解得x=4,h=10.
∴路灯有10m高.
18.解解:如图,过D作DE⊥BC的延长线于E,连接AD并延长交BC的延长线于F,
∵CD=4米,CD与地面成30°角,
∴DE=CD=×4=2米,根据勾股定理得,CE=米,
∵1米杆的影长为2米,
∴,
∴EF=2DE=2×2=4米,
∴BF=BC+CE+EF=10+2+4=(14+2)米,
∵,
∴AB=(14+2)=(7+)米.
答:电线杆的高度为(7+)m.
19.解:设墙上的影高CD落在地面上时的长度为xm,树高为hm,
∵某一时刻测得长为1m的竹竿影长为0.9m,墙上的影高CD为1.2m,
∴,解得x=1.08(m),
∴树的影长为:1.08+2.7=3.78(m),
∴,解得h=4.2(m).
答:测得的树高为4.2米.
20.解:(1)小明的站点D,旗杆的接地点B,标杆的接地点F,三点应在同一直线上.
(2)在测量过程中,如果标杆的位置确定,小明应该通过移动位置,直到小明的视点C,点E和点A在同一直线上为止.
故答案为:E和点A.
(3)答案不唯一.测量CD,EF,DF,FB即可.设测量得到CD=a,EF=b,DF=c,FB=d.
(4)作CH⊥AB于H,交EF于K.则四边形CDBH,四边形CDFK是矩形,
∴CK=DF=c,BF=KH=d,CD=FK=BH=a,EK=b﹣a.
∵EK∥AH,
∴△CKE∽△CHB,
∴=,
∴=,
∴AH=,
∴AB=AH+HB=+a=.
