沪科版九年级数学下册试题24.5 三角形的内切圆 一课一练(含答案)
文档属性
| 名称 | 沪科版九年级数学下册试题24.5 三角形的内切圆 一课一练(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 160.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-29 16:39:56 | ||
图片预览



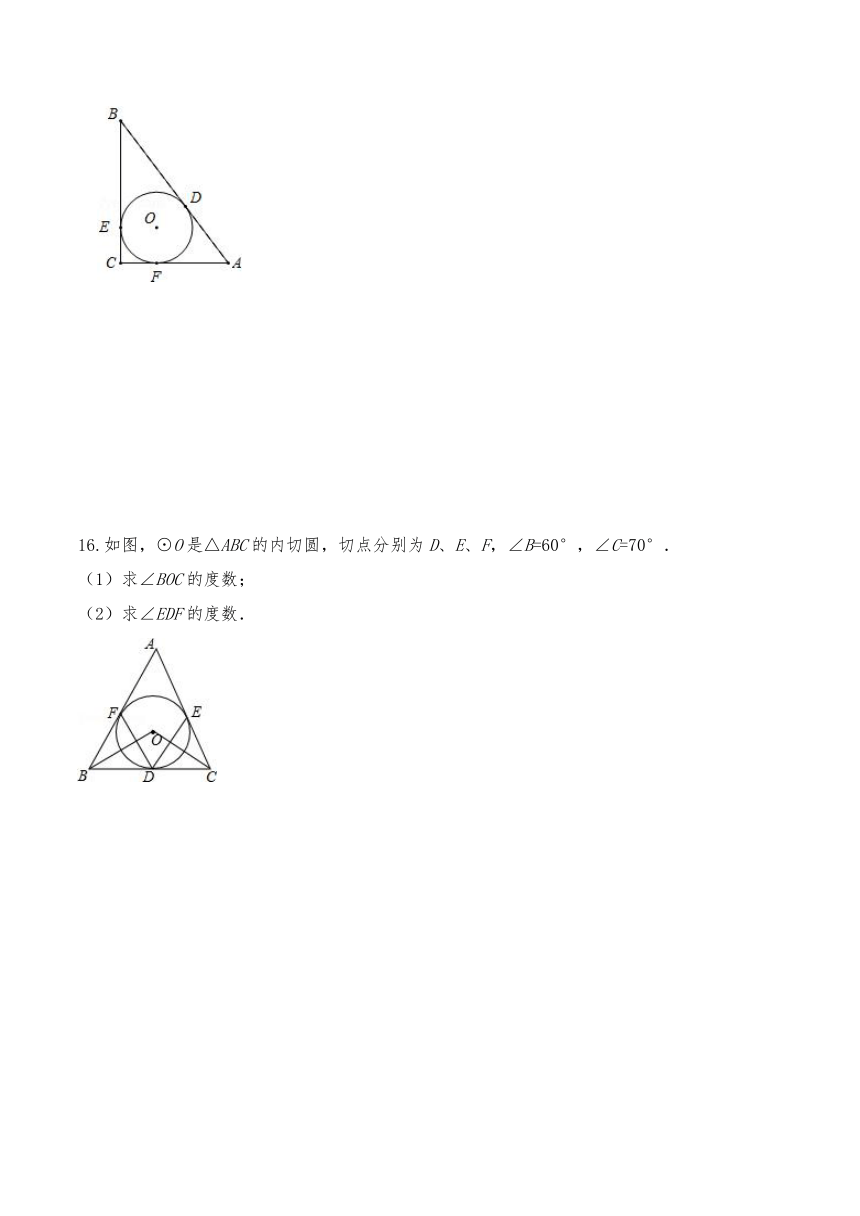
文档简介
24.5 三角形的内切圆
一、选择题
1.在Rt△ABC中,AB=6,BC=8,则这个三角形的内切圆的半径是( )
A.5 B.2 C.5或2 D.2或﹣1
2.如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,⊙O为△ABC的内切圆,点D是斜边AB的中点,则OD的长是( )
A. B.2 C.3 D.
3.如图,在△ABC中,∠BAC的平分线AD与∠ACB的平分线CE交于点O,下列说法正确的是( )
A.点O是△ABC的内切圆的圆心
B.CE⊥AB
C.△ABC的内切圆经过D,E两点
D.AO=CO
4.如图,△ABC中,∠ACB=90°,⊙O为△ABC的内切圆,切点分别为D、E、F.若AD=10,BC=5,则OB的长为( )
A.4 B. C. D.
5.下列关于三角形的内心说法正确的说法为( )
A.内心是三角形三个角平分线的交点
B.内心是三角形三边中垂线的交点
C.内心到三角形三个顶点的距离相等
D.钝角三角形的内心在三角形外
6.如图,四边形ABCD是矩形,点P是△ABD的内切圆的圆心,过P作PE⊥BC,PF⊥CD,垂足分别为点E、F,则四边形PECF和矩形ABCD的面积之比等于( )
A.1:2 B.2:3 C.3:4 D.无法确定
二、填空题
7.如图,Rt△ABC中,∠C=90°,AC=30cm,BC=40cm,现利用该三角形裁剪一个最大的圆,则该圆半径是 cm.
8.如图,△ABC是一块绿化带,将阴影部分修建为花圃,已知AB=15,AC=9,BC=12,阴影部分是△ABC的内切圆,一只自由飞翔的小鸟将随机落在这块绿化带上,则小鸟落在花圃上的概率为 .
9.如图,在△ABC中,AB=AC=5,BC=6,则△ABC的内切圆⊙I与外接圆⊙O的周长
之比为 .
10.如图,△ABC的内切圆与三边分别切于点D,E,F,若∠C=90°,AD=3,BD=5,则△ABC的面积为 .
11.直角三角形两条直角边分别为5和12,则此三角形的内切圆半径为 ,外接圆半径为 .
12.若直角三角形两边分别为6和8,则它内切圆的半径为 ﹣ .
13.如图,⊙I是△ABC的内切圆,与AB、BC、CA分别相切于点D、E、F,若∠DEF=50°,则∠A= .
14.如图,△ABC中,∠BAC=90°,∠B=30°,BC边上有一点P(不与点B,C重合),I为△APC的内心,若∠AIC的取值范围为m°<∠AIC<n°,则m+n= .
三、解答题
15.如图,在△ABC中,∠C=90°,⊙O是△ABC的内切圆,切点分别为D,E,F,若BD=6,AD=4,求⊙O的半径r.
16.如图,⊙O是△ABC的内切圆,切点分别为D、E、F,∠B=60°,∠C=70°.
(1)求∠BOC的度数;
(2)求∠EDF的度数.
17.如图,已知△ABC,∠B=40°.
(1)在图中,用尺规作出△ABC的内切圆O,并标出⊙O与边AB,BC,AC的切点D,E,F(保留痕迹,不必写作法);
(2)连接EF,DF,求∠EFD的度数.
18.如图,△ABC的内切圆⊙O与BC,CA,AB分别相切于D,E,F,且AB=9,BC=14,CA=13.求AF,BD,CE的长.
19.如图,点I是△ABC的内心,AI的延长线与边BC相交于点D,与△ABC的外接圆相交于点C.
求证:IE=BE.
20.已知:△ABC内接于⊙O,I是△ABC的内心,AD交BC于点E.求证:DB=DI.
答案
一、选择题
D.A.A.C.A.A.
二、填空题
7. 10.
8.
9. 12:25.
10. 15.
11. 2;6.5.
12.2或﹣1
13.80°.
14.255.
三、解答题
15.解:连接EO,FO,
∵⊙O是△ABC的内切圆,切点分别为D,E,F,
∴OE⊥BC,OF⊥AC,BD=BE,AD=AF,EC=CF,
又∵∠C=90°,
∴四边形ECFO是矩形,
又∵EO=FO,
∴矩形OECF是正方形,
设EO=x,
则EC=CF=x,
在Rt△ABC中
BC2+AC2=AB2
故(x+6)2+(x+4)2=102,
解得:x=2,
即⊙O的半径r=2.
16.解:
(1)∵⊙O是△ABC的内切圆,切点分别为D、E、F,
∴BO,CO分别是∠ABC和∠ACB的角平分线,
∴∠OBC=∠ABC=30°,∠OCB=∠ACB=35°,
∴∠BOC=180°﹣30°﹣35°=115°;
(2)如图所示;连接OE,OF.
∵∠ABC=60°,∠ACB=70°,
∴∠A=180°﹣60°﹣70°=50°.
∵AB是圆O的切线,
∴∠OFA=90°.
同理∠OEA=90°.
∴∠A+∠EOF=180°.
∴∠EOF=130°.
∴∠EDF=65°.
17.解:(1)如图1,
⊙O即为所求.
(2)如图2,
连接OD,OE,
∴OD⊥AB,OE⊥BC,
∴∠ODB=∠OEB=90°,
∵∠B=40°,
∴∠DOE=140°,
∴∠EFD=70°.
18.解:根据切线长定理,设AE=AF=xcm,BF=BD=ycm,CE=CD=zcm.根据题意,得
,
解得.
即AF=4cm、BD=5cm、CE=9cm.
19.证明:连接IB.
∵点I是△ABC的内心,
∴∠BAD=∠CAD,∠ABI=∠IBD.
又∵∠CAD=∠DBE
∴∠BIE=∠BAD+∠ABI=∠CAD+∠IBD=∠IBD+∠DBE=∠IBE,
∴BE=IE.
20.证明:∵点I是△ABC的内心,
∴∠BAD=∠CAD,∠ABI=∠CBI,
∵∠CBD=∠CAD,
∴∠BAD=∠CBD,
∵∠BID=∠ABI+∠BAD,∠IBD=∠CBI+∠CBD,
∴∠BID=∠IBD,
∴ID=BD.
一、选择题
1.在Rt△ABC中,AB=6,BC=8,则这个三角形的内切圆的半径是( )
A.5 B.2 C.5或2 D.2或﹣1
2.如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,⊙O为△ABC的内切圆,点D是斜边AB的中点,则OD的长是( )
A. B.2 C.3 D.
3.如图,在△ABC中,∠BAC的平分线AD与∠ACB的平分线CE交于点O,下列说法正确的是( )
A.点O是△ABC的内切圆的圆心
B.CE⊥AB
C.△ABC的内切圆经过D,E两点
D.AO=CO
4.如图,△ABC中,∠ACB=90°,⊙O为△ABC的内切圆,切点分别为D、E、F.若AD=10,BC=5,则OB的长为( )
A.4 B. C. D.
5.下列关于三角形的内心说法正确的说法为( )
A.内心是三角形三个角平分线的交点
B.内心是三角形三边中垂线的交点
C.内心到三角形三个顶点的距离相等
D.钝角三角形的内心在三角形外
6.如图,四边形ABCD是矩形,点P是△ABD的内切圆的圆心,过P作PE⊥BC,PF⊥CD,垂足分别为点E、F,则四边形PECF和矩形ABCD的面积之比等于( )
A.1:2 B.2:3 C.3:4 D.无法确定
二、填空题
7.如图,Rt△ABC中,∠C=90°,AC=30cm,BC=40cm,现利用该三角形裁剪一个最大的圆,则该圆半径是 cm.
8.如图,△ABC是一块绿化带,将阴影部分修建为花圃,已知AB=15,AC=9,BC=12,阴影部分是△ABC的内切圆,一只自由飞翔的小鸟将随机落在这块绿化带上,则小鸟落在花圃上的概率为 .
9.如图,在△ABC中,AB=AC=5,BC=6,则△ABC的内切圆⊙I与外接圆⊙O的周长
之比为 .
10.如图,△ABC的内切圆与三边分别切于点D,E,F,若∠C=90°,AD=3,BD=5,则△ABC的面积为 .
11.直角三角形两条直角边分别为5和12,则此三角形的内切圆半径为 ,外接圆半径为 .
12.若直角三角形两边分别为6和8,则它内切圆的半径为 ﹣ .
13.如图,⊙I是△ABC的内切圆,与AB、BC、CA分别相切于点D、E、F,若∠DEF=50°,则∠A= .
14.如图,△ABC中,∠BAC=90°,∠B=30°,BC边上有一点P(不与点B,C重合),I为△APC的内心,若∠AIC的取值范围为m°<∠AIC<n°,则m+n= .
三、解答题
15.如图,在△ABC中,∠C=90°,⊙O是△ABC的内切圆,切点分别为D,E,F,若BD=6,AD=4,求⊙O的半径r.
16.如图,⊙O是△ABC的内切圆,切点分别为D、E、F,∠B=60°,∠C=70°.
(1)求∠BOC的度数;
(2)求∠EDF的度数.
17.如图,已知△ABC,∠B=40°.
(1)在图中,用尺规作出△ABC的内切圆O,并标出⊙O与边AB,BC,AC的切点D,E,F(保留痕迹,不必写作法);
(2)连接EF,DF,求∠EFD的度数.
18.如图,△ABC的内切圆⊙O与BC,CA,AB分别相切于D,E,F,且AB=9,BC=14,CA=13.求AF,BD,CE的长.
19.如图,点I是△ABC的内心,AI的延长线与边BC相交于点D,与△ABC的外接圆相交于点C.
求证:IE=BE.
20.已知:△ABC内接于⊙O,I是△ABC的内心,AD交BC于点E.求证:DB=DI.
答案
一、选择题
D.A.A.C.A.A.
二、填空题
7. 10.
8.
9. 12:25.
10. 15.
11. 2;6.5.
12.2或﹣1
13.80°.
14.255.
三、解答题
15.解:连接EO,FO,
∵⊙O是△ABC的内切圆,切点分别为D,E,F,
∴OE⊥BC,OF⊥AC,BD=BE,AD=AF,EC=CF,
又∵∠C=90°,
∴四边形ECFO是矩形,
又∵EO=FO,
∴矩形OECF是正方形,
设EO=x,
则EC=CF=x,
在Rt△ABC中
BC2+AC2=AB2
故(x+6)2+(x+4)2=102,
解得:x=2,
即⊙O的半径r=2.
16.解:
(1)∵⊙O是△ABC的内切圆,切点分别为D、E、F,
∴BO,CO分别是∠ABC和∠ACB的角平分线,
∴∠OBC=∠ABC=30°,∠OCB=∠ACB=35°,
∴∠BOC=180°﹣30°﹣35°=115°;
(2)如图所示;连接OE,OF.
∵∠ABC=60°,∠ACB=70°,
∴∠A=180°﹣60°﹣70°=50°.
∵AB是圆O的切线,
∴∠OFA=90°.
同理∠OEA=90°.
∴∠A+∠EOF=180°.
∴∠EOF=130°.
∴∠EDF=65°.
17.解:(1)如图1,
⊙O即为所求.
(2)如图2,
连接OD,OE,
∴OD⊥AB,OE⊥BC,
∴∠ODB=∠OEB=90°,
∵∠B=40°,
∴∠DOE=140°,
∴∠EFD=70°.
18.解:根据切线长定理,设AE=AF=xcm,BF=BD=ycm,CE=CD=zcm.根据题意,得
,
解得.
即AF=4cm、BD=5cm、CE=9cm.
19.证明:连接IB.
∵点I是△ABC的内心,
∴∠BAD=∠CAD,∠ABI=∠IBD.
又∵∠CAD=∠DBE
∴∠BIE=∠BAD+∠ABI=∠CAD+∠IBD=∠IBD+∠DBE=∠IBE,
∴BE=IE.
20.证明:∵点I是△ABC的内心,
∴∠BAD=∠CAD,∠ABI=∠CBI,
∵∠CBD=∠CAD,
∴∠BAD=∠CBD,
∵∠BID=∠ABI+∠BAD,∠IBD=∠CBI+∠CBD,
∴∠BID=∠IBD,
∴ID=BD.
