2023年安徽省马鞍山中考数学 仿真 模拟试卷(含答案)
文档属性
| 名称 | 2023年安徽省马鞍山中考数学 仿真 模拟试卷(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 243.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-29 00:00:00 | ||
图片预览



文档简介
2023年安徽省马鞍山中考数学 仿真 模拟试卷
一、选择题(本大题共10小题,共40.0分)
1. 的相反数是( )
A. B. C. D.
2. 截止到年底,中国十大储蓄省排名出炉,河南省以“万亿”规模位列榜单,数据“万亿”用科学记数法表示为( )
A. B. C. D.
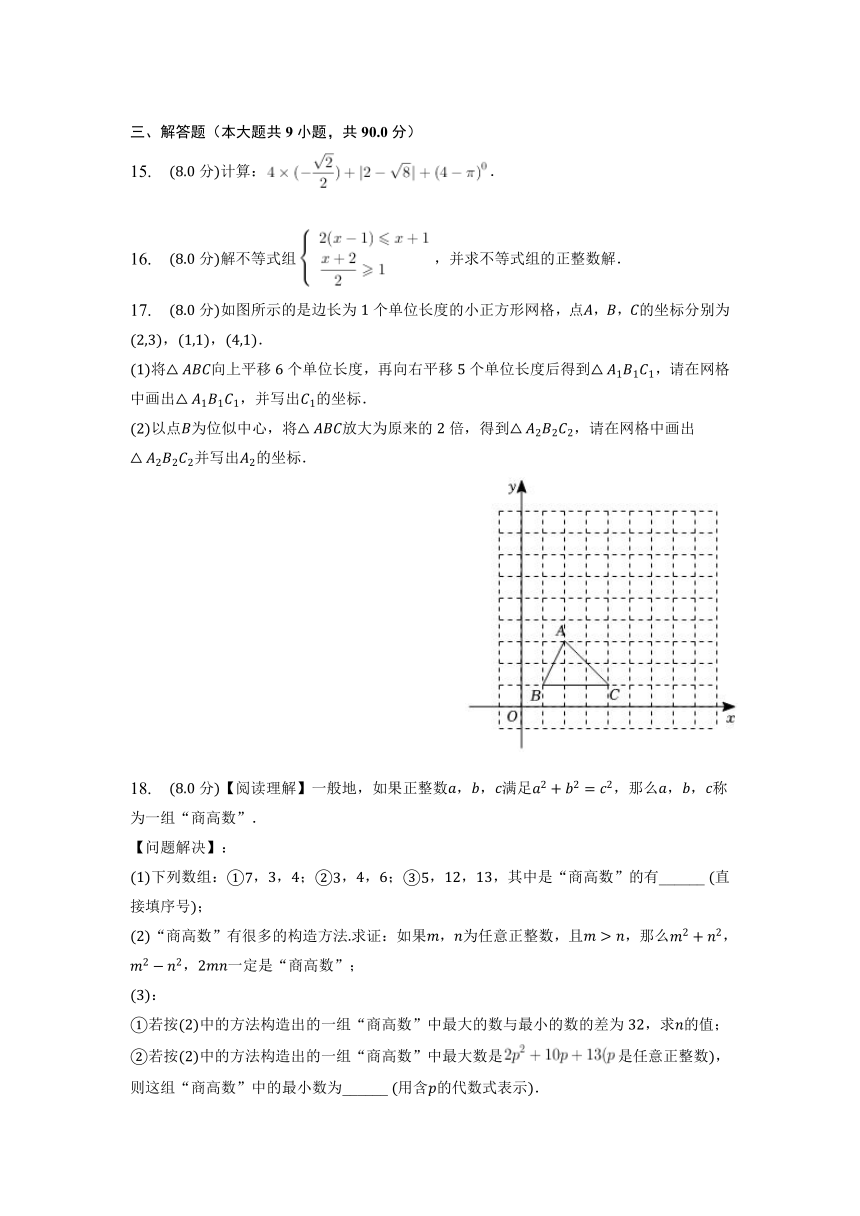
3. 已知组合体如图,则从正面看该组合体得到的图形是( )
A.
B.
C.
D.
4. 下列运算一定正确的是( )
A. B.
C. D.
5. 如图,两条直线,中,,,顶点、分别在和上,,则的度数是( )
A.
B.
C.
D.
6. 若关于的一元二次方程有实数根,则的取值范围是( )
A. B. C. 且 D. 且
7. 质检人员从编号为,,,,的五种不同产品中随机抽取一种进行质量检测,所抽到的产品编号不小于的概率为( )
A. . B. C. D.
8. 在同一直角坐标系中,一次函数与反比例函数的图象位置可能是( )
A. B. C. D.
9. 如图,纸板中,,,,是上一点,沿过点的直线剪下一个与相似的小三角形纸板,如果有种不同剪法,那么长的取值范围( )
A. B. C. D.
10. 菱形中,,,,分别是,上的动点,且,连接,交于,则下列结论:≌;为等边三角形;的最小值为其中正确的结论是( )
A. B.
C. D.
二、填空题(本大题共4小题,共20.0分)
11. 分解因式: ______ .
12. 要使得式子有意义,则的取值范围是 .
13. 面积为的平行四边形在平面直角坐标系中如图所示,反比例函数为常数,,的图象经过点与的中点,则 ______ .
14. 如图,函数经过点,对称轴为直线:;;;;若点、在抛物线上,则;为任意实数,其中结论正确的有 .
三、解答题(本大题共9小题,共90.0分)
15. 分计算:.
16. 分解不等式组,并求不等式组的正整数解.
17. 分如图所示的是边长为个单位长度的小正方形网格,点,,的坐标分别为,,.
将向上平移个单位长度,再向右平移个单位长度后得到,请在网格中画出,并写出的坐标.
以点为位似中心,将放大为原来的倍,得到,请在网格中画出并写出的坐标.
18. 分【阅读理解】一般地,如果正整数,,满足,那么,,称为一组“商高数”.
【问题解决】:
下列数组:,,;,,;,,,其中是“商高数”的有______ 直接填序号;
“商高数”有很多的构造方法求证:如果,为任意正整数,且,那么,,一定是“商高数”;
:
若按中的方法构造出的一组“商高数”中最大的数与最小的数的差为,求的值;
若按中的方法构造出的一组“商高数”中最大数是是任意正整数,则这组“商高数”中的最小数为______ 用含的代数式表示.
19. 分小明家为相应政府“全民健身”号召,准备买一台跑步机,周末和家人一起去科尼斯百货购买,爱动脑筋的小明想用刚刚学过的三角函数的有关知识求助跑步机踏板的长度图分别是某种型号跑步机的实物图与示意图,已知跑步机手柄的一端的高度约为,踏板与地面的夹角为,支架长为,为求跑步机踏板的长度精确到.
参考数据:,,
20. 分如图,线段是的直径,延长至点,使,点是线段的中点,交于点,连接.
求证:是的切线;
点是上一动点不与点,重合,连接,求的值.
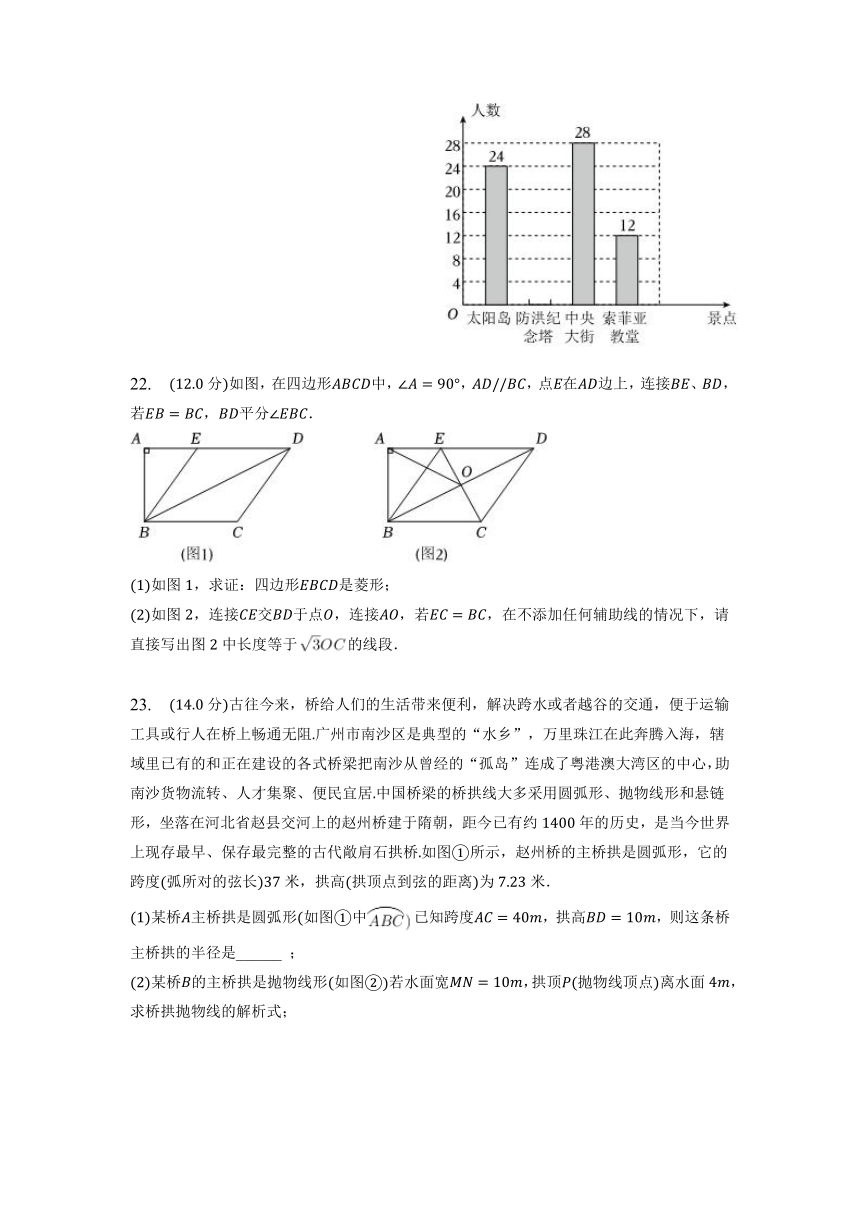
21. 分某中学开展了以“我最喜欢的家乡景点”为主题的调查活动,围绕“在太阳岛、防洪纪念塔、中央大街、索菲亚教堂四个景点中,你最喜欢哪一个?必选且只选一个”的问题,在全校范围内随机抽取部分学生进行问卷调查,将调查结果整理后绘制成如图所示的不完整的条形统计图,其中最喜欢太阳岛的学生人数占所调查人数的请你根据图中提供的信息解答下列问题:
在这次调查中,一共抽取了多少名学生?
请通过计算补全条形统计图;
若该中学共有名学生,请你估计该中学最喜欢中央大街的学生共有多少名.
22. 分如图,在四边形中,,,点在边上,连接、,若,平分.
如图,求证:四边形是菱形;
如图,连接交于点,连接,若,在不添加任何辅助线的情况下,请直接写出图中长度等于的线段.
23. 分古往今来,桥给人们的生活带来便利,解决跨水或者越谷的交通,便于运输工具或行人在桥上畅通无阻广州市南沙区是典型的“水乡”,万里珠江在此奔腾入海,辖域里已有的和正在建设的各式桥梁把南沙从曾经的“孤岛”连成了粤港澳大湾区的中心,助南沙货物流转、人才集聚、便民宜居中国桥梁的桥拱线大多采用圆弧形、抛物线形和悬链形,坐落在河北省赵县交河上的赵州桥建于隋朝,距今已有约年的历史,是当今世界上现存最早、保存最完整的古代敞肩石拱桥如图所示,赵州桥的主桥拱是圆弧形,它的跨度弧所对的弦长米,拱高拱顶点到弦的距离为米.
某桥主桥拱是圆弧形如图中已知跨度,拱高,则这条桥主桥拱的半径是______ ;
某桥的主桥拱是抛物线形如图若水面宽,拱顶抛物线顶点离水面,求桥拱抛物线的解析式;
如图,某时桥和桥的桥下水位均上升了,求此时两桥的水面宽度.
1. 2. 3. 4. 5.
6. 7. 8. 9. 10.
11.
12.且
13.
14.
15.解:
.
16.解:,
解不等式得:,
解不等式得:,
原不等式组的解集为:.
原不等式组的正整数解为:,,.
17.解:如图所示,即为所求,,
解:如图所示,即为所求,.
18.解:(1)①∵32+42≠72,
∴7,3,4不是“商高数”,
②∵32+42≠62,
∴6,3,4不是“商高数”,
③∵52+122=132,
∴5,12,13是“商高数”,
故答案为:③;
(2)(m2-n2)2+(2nn)2=(m2+n2)2,
∴m2+n2,m2-n2,2mn一定是“商高数;
(3)①∵m2+n2>m2-n2,m2+n2>2mn,
∴当(m2+n2)-(m2-n2)=32,
解得:n=4,
当(m2+n2)-2mn=32,
解得:m-n=4(不合题意,舍去);
②∵2p2+10p+13=p2+4p+4+p2+6p+9=(p+2)2+(p+3)2,
∵p是任意正整数,
∴p+2<p+3,
故答案为:p+2.
19.解:过点作于,交于.
与地面的夹角为,为,
,
,
在中,,
则.
在中,,
跑步机踏板的长度约为.
20.证明:如图中,连接,,
点是线段的中点,交于点,
垂直平分,
,.
,
,
是等边三角形,
,
,且为的外角,
,
,
,
为的半径,
是的切线;
解:连接,如图,
由已知可得:.
,
又,
∽,
.
21.解:名,
答:在这次调查中,一共抽取了名学生;
名,
补全条形图如下:
名,
答:估计该中学最喜欢中央大街的学生共大约有名.
22.证明:,
,
平分,
,
,
,
,
,
,
四边形是平行四边形,
,
平行四边形是菱形;
解:如图,平行四边形是菱形,
,,,,
,
,
是等边三角形,
,
,
;
,
;
,
,
,
,
,
,
是等边三角形,
;
图中长度等于的线段的线段是、、、.
23.解(1)连接OA,延长BD,由垂径定理知BD延长线经过点O,
设弧AB所在圆的半径为R米,
由题意得:OD⊥AB,CD=10,
则AD=BD=20,OD=R-8;
由勾股定理得:R2=202+(R-10)2,
解得:R=25,
即弧AB所在圆的半径为25m.
故答案为:25;
(2)如图所示,以水面所在直线为x轴,MN的中点为原点,建立平面直角坐标系,
依题意,P(0,4),M(-5,0),
设抛物线解析式为y=ax2+4,将点M(-5,0)代入得,
25a+4=0,
解得:a=-,
∴抛物线解析式为y=-x2+4;
(3)如图所示,依题意,GD=2,
则BG=10-2=8,
∴GO=r-BG=25-8=17,
在Rt△OGE中,
EG===4,
∴EF=2EG=8,
则水面宽度为8米;
由(1)可得抛物线解析式为y=-425x2+4,如图所示,
当水面上涨2米时,
即当y=2时,2=-x2+4,
解得:x1=,x2=-,
∴水面宽度为5米.
一、选择题(本大题共10小题,共40.0分)
1. 的相反数是( )
A. B. C. D.
2. 截止到年底,中国十大储蓄省排名出炉,河南省以“万亿”规模位列榜单,数据“万亿”用科学记数法表示为( )
A. B. C. D.
3. 已知组合体如图,则从正面看该组合体得到的图形是( )
A.
B.
C.
D.
4. 下列运算一定正确的是( )
A. B.
C. D.
5. 如图,两条直线,中,,,顶点、分别在和上,,则的度数是( )
A.
B.
C.
D.
6. 若关于的一元二次方程有实数根,则的取值范围是( )
A. B. C. 且 D. 且
7. 质检人员从编号为,,,,的五种不同产品中随机抽取一种进行质量检测,所抽到的产品编号不小于的概率为( )
A. . B. C. D.
8. 在同一直角坐标系中,一次函数与反比例函数的图象位置可能是( )
A. B. C. D.
9. 如图,纸板中,,,,是上一点,沿过点的直线剪下一个与相似的小三角形纸板,如果有种不同剪法,那么长的取值范围( )
A. B. C. D.
10. 菱形中,,,,分别是,上的动点,且,连接,交于,则下列结论:≌;为等边三角形;的最小值为其中正确的结论是( )
A. B.
C. D.
二、填空题(本大题共4小题,共20.0分)
11. 分解因式: ______ .
12. 要使得式子有意义,则的取值范围是 .
13. 面积为的平行四边形在平面直角坐标系中如图所示,反比例函数为常数,,的图象经过点与的中点,则 ______ .
14. 如图,函数经过点,对称轴为直线:;;;;若点、在抛物线上,则;为任意实数,其中结论正确的有 .
三、解答题(本大题共9小题,共90.0分)
15. 分计算:.
16. 分解不等式组,并求不等式组的正整数解.
17. 分如图所示的是边长为个单位长度的小正方形网格,点,,的坐标分别为,,.
将向上平移个单位长度,再向右平移个单位长度后得到,请在网格中画出,并写出的坐标.
以点为位似中心,将放大为原来的倍,得到,请在网格中画出并写出的坐标.
18. 分【阅读理解】一般地,如果正整数,,满足,那么,,称为一组“商高数”.
【问题解决】:
下列数组:,,;,,;,,,其中是“商高数”的有______ 直接填序号;
“商高数”有很多的构造方法求证:如果,为任意正整数,且,那么,,一定是“商高数”;
:
若按中的方法构造出的一组“商高数”中最大的数与最小的数的差为,求的值;
若按中的方法构造出的一组“商高数”中最大数是是任意正整数,则这组“商高数”中的最小数为______ 用含的代数式表示.
19. 分小明家为相应政府“全民健身”号召,准备买一台跑步机,周末和家人一起去科尼斯百货购买,爱动脑筋的小明想用刚刚学过的三角函数的有关知识求助跑步机踏板的长度图分别是某种型号跑步机的实物图与示意图,已知跑步机手柄的一端的高度约为,踏板与地面的夹角为,支架长为,为求跑步机踏板的长度精确到.
参考数据:,,
20. 分如图,线段是的直径,延长至点,使,点是线段的中点,交于点,连接.
求证:是的切线;
点是上一动点不与点,重合,连接,求的值.
21. 分某中学开展了以“我最喜欢的家乡景点”为主题的调查活动,围绕“在太阳岛、防洪纪念塔、中央大街、索菲亚教堂四个景点中,你最喜欢哪一个?必选且只选一个”的问题,在全校范围内随机抽取部分学生进行问卷调查,将调查结果整理后绘制成如图所示的不完整的条形统计图,其中最喜欢太阳岛的学生人数占所调查人数的请你根据图中提供的信息解答下列问题:
在这次调查中,一共抽取了多少名学生?
请通过计算补全条形统计图;
若该中学共有名学生,请你估计该中学最喜欢中央大街的学生共有多少名.
22. 分如图,在四边形中,,,点在边上,连接、,若,平分.
如图,求证:四边形是菱形;
如图,连接交于点,连接,若,在不添加任何辅助线的情况下,请直接写出图中长度等于的线段.
23. 分古往今来,桥给人们的生活带来便利,解决跨水或者越谷的交通,便于运输工具或行人在桥上畅通无阻广州市南沙区是典型的“水乡”,万里珠江在此奔腾入海,辖域里已有的和正在建设的各式桥梁把南沙从曾经的“孤岛”连成了粤港澳大湾区的中心,助南沙货物流转、人才集聚、便民宜居中国桥梁的桥拱线大多采用圆弧形、抛物线形和悬链形,坐落在河北省赵县交河上的赵州桥建于隋朝,距今已有约年的历史,是当今世界上现存最早、保存最完整的古代敞肩石拱桥如图所示,赵州桥的主桥拱是圆弧形,它的跨度弧所对的弦长米,拱高拱顶点到弦的距离为米.
某桥主桥拱是圆弧形如图中已知跨度,拱高,则这条桥主桥拱的半径是______ ;
某桥的主桥拱是抛物线形如图若水面宽,拱顶抛物线顶点离水面,求桥拱抛物线的解析式;
如图,某时桥和桥的桥下水位均上升了,求此时两桥的水面宽度.
1. 2. 3. 4. 5.
6. 7. 8. 9. 10.
11.
12.且
13.
14.
15.解:
.
16.解:,
解不等式得:,
解不等式得:,
原不等式组的解集为:.
原不等式组的正整数解为:,,.
17.解:如图所示,即为所求,,
解:如图所示,即为所求,.
18.解:(1)①∵32+42≠72,
∴7,3,4不是“商高数”,
②∵32+42≠62,
∴6,3,4不是“商高数”,
③∵52+122=132,
∴5,12,13是“商高数”,
故答案为:③;
(2)(m2-n2)2+(2nn)2=(m2+n2)2,
∴m2+n2,m2-n2,2mn一定是“商高数;
(3)①∵m2+n2>m2-n2,m2+n2>2mn,
∴当(m2+n2)-(m2-n2)=32,
解得:n=4,
当(m2+n2)-2mn=32,
解得:m-n=4(不合题意,舍去);
②∵2p2+10p+13=p2+4p+4+p2+6p+9=(p+2)2+(p+3)2,
∵p是任意正整数,
∴p+2<p+3,
故答案为:p+2.
19.解:过点作于,交于.
与地面的夹角为,为,
,
,
在中,,
则.
在中,,
跑步机踏板的长度约为.
20.证明:如图中,连接,,
点是线段的中点,交于点,
垂直平分,
,.
,
,
是等边三角形,
,
,且为的外角,
,
,
,
为的半径,
是的切线;
解:连接,如图,
由已知可得:.
,
又,
∽,
.
21.解:名,
答:在这次调查中,一共抽取了名学生;
名,
补全条形图如下:
名,
答:估计该中学最喜欢中央大街的学生共大约有名.
22.证明:,
,
平分,
,
,
,
,
,
,
四边形是平行四边形,
,
平行四边形是菱形;
解:如图,平行四边形是菱形,
,,,,
,
,
是等边三角形,
,
,
;
,
;
,
,
,
,
,
,
是等边三角形,
;
图中长度等于的线段的线段是、、、.
23.解(1)连接OA,延长BD,由垂径定理知BD延长线经过点O,
设弧AB所在圆的半径为R米,
由题意得:OD⊥AB,CD=10,
则AD=BD=20,OD=R-8;
由勾股定理得:R2=202+(R-10)2,
解得:R=25,
即弧AB所在圆的半径为25m.
故答案为:25;
(2)如图所示,以水面所在直线为x轴,MN的中点为原点,建立平面直角坐标系,
依题意,P(0,4),M(-5,0),
设抛物线解析式为y=ax2+4,将点M(-5,0)代入得,
25a+4=0,
解得:a=-,
∴抛物线解析式为y=-x2+4;
(3)如图所示,依题意,GD=2,
则BG=10-2=8,
∴GO=r-BG=25-8=17,
在Rt△OGE中,
EG===4,
∴EF=2EG=8,
则水面宽度为8米;
由(1)可得抛物线解析式为y=-425x2+4,如图所示,
当水面上涨2米时,
即当y=2时,2=-x2+4,
解得:x1=,x2=-,
∴水面宽度为5米.
同课章节目录
