2023年湖北省荆州市中考数学综合练习题(含答案)
文档属性
| 名称 | 2023年湖北省荆州市中考数学综合练习题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 387.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-29 17:22:36 | ||
图片预览




文档简介
2023年荆州中考数学综合练习题
姓名 分数
一、选择题(每小题3分,共30分)
1. 下列各数中与2互为相反数的是( )
A. B. C. D.
2. 已知:点P(3-m,m-1)关于x轴对称的点在第三象限,则m的取值范围在数轴上表示正确的是( )
3. 某市为了方便市民绿色出行,推出了共享单车服务.图①是某品牌共享单车放在水平地面的实物图,图②是其示意图,其中AB,CD都与地面l平行,∠BCD=60°,∠BAC=54°.当∠MAC为( )度时,AM与CB平行.
A.16 B.60 C.66 D.114
4. 下列各式中无意义的是( )
A. B. C. D.
5. 为选拔一位同学参加校运会50米跑项目,九(1)班班委对甲,乙,丙,丁4位同学进行了50米跑的多次测试,现将四位同学的测试数据整理在表格中,则应该选择( )参加比赛.
甲 乙 丙 丁
平均用时/秒 8.2 7.9 7.9 8.2
方差 2.2 1.4 2.4 1.4
A.甲 B.乙 C.丙 D.丁
6. 如图,有一池塘,要测池塘两端A,B的距离,可先在地上取一个点C,从点C不经过池塘可以直接到达点A和B.连接AC并延长到点D,使CD=CA.连接BC并延长到点E,使CE=CB.连接DE,根据两个三角形全等,那么量出DE的长就知道A、B的距离.判断图中两个三角形全等的依据是( )
A.SAS B.SSS C.ASA D.AAS
7. 我国古代数学名著《四元玉鉴》中记载:“九百九十九文钱,及时梨果买一千,一十一文梨九个,七枚果子四文钱.问梨果各几何?”意思是:用999文钱买得梨和果共1000个,梨11文买9个,果4文买7个,问梨果各买了多少个?如果设梨买x个,果买y个,那么可列方程组为( )
A. B. C. D.
8. 佳佳和爸爸一起从家出发,匀速行走25min后抵达离家1000m的报亭,佳佳随即按原速返回,爸爸看了10min报后返回,恰好与佳佳同时到家.则表示爸爸离家后距离与时间关系的大致图象是( )
A. B. C. D.
9. 如图所示,在△ABC中,BC=3,AC=4,∠ACB=90°,以点B为圆心,BC长为半径画弧,与AB交于点D,再分别以A、D为圆心,大于的长为半径画弧,两弧交于点E、F,作直线EF,分别交AC、AB于点P、Q,则PQ的长度为( )
A. B. C. D.
10. 如图,在直角坐标系中,Rt△OAB的边OB在y轴上,∠ABO=90°,AB=3,点C在AB上,BC=AB,且∠BOC=∠A,若双曲线y=经过点C,则k的值为( )
A. B. C.1 D.2
二、填空题(每小题3分,共18分
11. 分别写出数字、、、的四张卡片中,除数字外其他均相同,从中随机抽取一张是无理数的概率是 .
12. 如图,三角形ABC中,∠ACB=90°,AC=6,BC=8,P为直线AB上一动点,连PC,则线段PC的最小值是 .
13. 设m,n是方程的两个实数根,则的值为______.
14. 如图是一个正方体的展开图,将它折叠成正方体后,“数”字的对面上的文字是
15. 如图,某居民楼MN后有一个小山坡AC,其坡度为i=1:2.4(注:坡度是指坡面的铅直高度与水平宽度的比),小区准备在小山坡上加装广告牌PQ.已知广告牌底端Q到坡底A的距离为5.2米,水平地面上居民楼MN到坡底A的距离为1.2米,当太阳光线与水平线成53°角时,测得广告牌PQ落在居民楼上的影子DN长为3米.则广告牌PQ的高为 .(参考数据:)
16. 如图,在平面直角坐标系xOy中,点A在x轴负半轴上,点B在y轴正半轴上,⊙D经过A,B,O,C四点,,,则圆心点D的坐标是
三、解答题(共72分)
17.(8分)已知不等式的最小整数解是方程的解,求a的值.
18.(8分)先化简:,再在不等式组的整数解中取一个合适的代入求值.
19.(8分)如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD.
(1)证明:BD=CD; (2)当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.
20.(8分)中华文化源远流长,文学方面,《西游记》《三国演义》《水浒传》《红楼梦》是我国古代长篇小说中的典型代表,就“四大古典名著你读完了几部”的问题在全校学生中进行了抽样调查,根据调查结果绘制成如下尚不完整的统计图.
请根据以上信息,解决下列问题
(1)本次调查所得数据的众数是 部,中位数是 部;
(2)扇形统计图中“4部”所在扇形的圆心角为 度;
(3)请将条形统计图补充完整;
(4)没有读过四大古典名著的两名学生准备从中各自随机选择一部来阅读,求他们恰好选中同一名著的概率.
21.(8分)如图,已知⊙O经过菱形ABCD的顶点A,C,且与CD相切,直径CF交AB于点E.
(1)求证:AD与⊙O相切;(2)若,求的值.
22.(10分)“冰墩墩”和“雪容融”作为北京冬奥会和残奥会的吉祥物深受大家喜爱,某旗舰店销售“冰墩墩”毛绒玩具总额为24000元,销售“雪容融”毛绒玩具总额为8000元,其中“冰墩墩”的销售单价比“雪容融”的销售单价多40元,并且销售“冰墩墩”的数量是“雪容融”数量的2倍.
(1)求“冰墩墩”和“雪容融”的销售单价分别是多少元?
(2)已知“冰墩墩”和“雪容融”的成本分别为100元/个和60元/个,进入2022年1月后,这两款毛绒玩具持续热销,于是该旗舰店再购进了这两款毛绒玩具共800个,其中“雪容融”的数量不超过“冰墩墩”数量的3倍,且这两款毛绒玩具购进总价不超过57600元.为回馈新老客户,该旗舰店决定对“冰墩墩”降价10%后再销售,若1月份购进的这两款毛绒玩具全部售出,则“冰墩墩”购进多少个时该旗舰店当月销售利润最大,并求出最大利润.
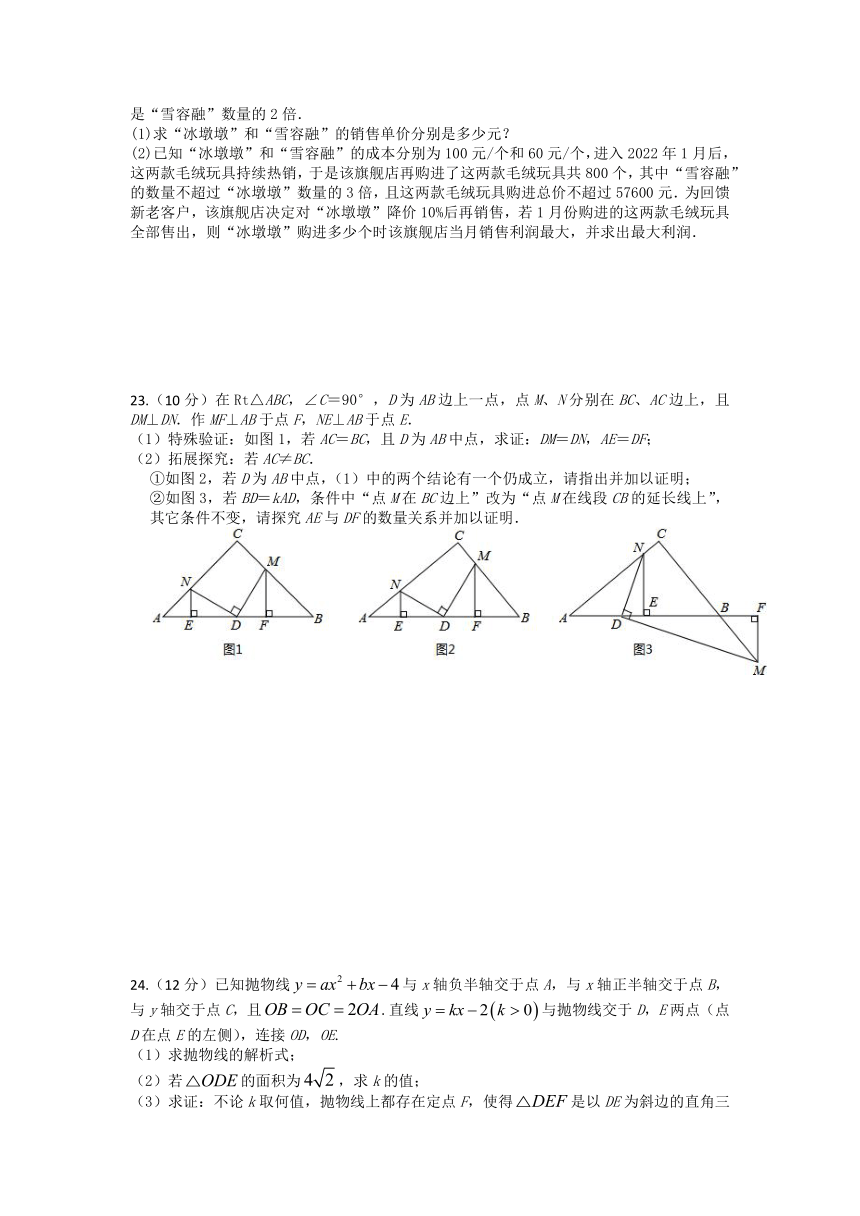
23.(10分)在Rt△ABC,∠C=90°,D为AB边上一点,点M、N分别在BC、AC边上,且DM⊥DN.作MF⊥AB于点F,NE⊥AB于点E.
(1)特殊验证:如图1,若AC=BC,且D为AB中点,求证:DM=DN,AE=DF;
(2)拓展探究:若AC≠BC.
①如图2,若D为AB中点,(1)中的两个结论有一个仍成立,请指出并加以证明;
②如图3,若BD=kAD,条件中“点M在BC边上”改为“点M在线段CB的延长线上”,其它条件不变,请探究AE与DF的数量关系并加以证明.
24.(12分)已知抛物线与x轴负半轴交于点A,与x轴正半轴交于点B,与y轴交于点C,且.直线与抛物线交于D,E两点(点D在点E的左侧),连接OD,OE.
(1)求抛物线的解析式;
(2)若的面积为,求k的值;
(3)求证:不论k取何值,抛物线上都存在定点F,使得是以DE为斜边的直角三角形.
2023年荆州中考数学综合练习题
姓名 分数
一、选择题(每小题3分,共30分)
1. 下列各数中与2互为相反数的是( D )
A. B. C. D.
2. 已知:点P(3-m,m-1)关于x轴对称的点在第三象限,则m的取值范围在数轴上表示正确的是( A )
3. 某市为了方便市民绿色出行,推出了共享单车服务.图①是某品牌共享单车放在水平地面的实物图,图②是其示意图,其中AB,CD都与地面l平行,∠BCD=60°,∠BAC=54°.当∠MAC为( C )度时,AM与CB平行.
A.16 B.60 C.66 D.114
4. 下列各式中无意义的是( D )
A. B. C. D.
5. 为选拔一位同学参加校运会50米跑项目,九(1)班班委对甲,乙,丙,丁4位同学进行了50米跑的多次测试,现将四位同学的测试数据整理在表格中,则应该选择( B )参加比赛.
甲 乙 丙 丁
平均用时/秒 8.2 7.9 7.9 8.2
方差 2.2 1.4 2.4 1.4
A.甲 B.乙 C.丙 D.丁
6. 如图,有一池塘,要测池塘两端A,B的距离,可先在地上取一个点C,从点C不经过池塘可以直接到达点A和B.连接AC并延长到点D,使CD=CA.连接BC并延长到点E,使CE=CB.连接DE,根据两个三角形全等,那么量出DE的长就知道A、B的距离.判断图中两个三角形全等的依据是( A )
A.SAS B.SSS C.ASA D.AAS
7. 我国古代数学名著《四元玉鉴》中记载:“九百九十九文钱,及时梨果买一千,一十一文梨九个,七枚果子四文钱.问梨果各几何?”意思是:用999文钱买得梨和果共1000个,梨11文买9个,果4文买7个,问梨果各买了多少个?如果设梨买x个,果买y个,那么可列方程组为( A )
A. B. C. D.
8. 佳佳和爸爸一起从家出发,匀速行走25min后抵达离家1000m的报亭,佳佳随即按原速返回,爸爸看了10min报后返回,恰好与佳佳同时到家.则表示爸爸离家后距离与时间关系的大致图象是( B )
A. B. C. D.
9. 如图所示,在△ABC中,BC=3,AC=4,∠ACB=90°,以点B为圆心,BC长为半径画弧,与AB交于点D,再分别以A、D为圆心,大于的长为半径画弧,两弧交于点E、F,作直线EF,分别交AC、AB于点P、Q,则PQ的长度为( B )
A. B. C. D.
10. 如图,在直角坐标系中,Rt△OAB的边OB在y轴上,∠ABO=90°,AB=3,点C在AB上,BC=AB,且∠BOC=∠A,若双曲线y=经过点C,则k的值为( B )
A. B. C.1 D.2
二、填空题(每小题3分,共18分
11. 分别写出数字、、、的四张卡片中,除数字外其他均相同,从中随机抽取一张是无理数的概率是____.
12. 如图,三角形ABC中,∠ACB=90°,AC=6,BC=8,P为直线AB上一动点,连PC,则线段PC的最小值是 .
13. 设m,n是方程的两个实数根,则的值为___-1___.
14. 如图是一个正方体的展开图,将它折叠成正方体后,“数”字的对面上的文字是 试
15. 如图,某居民楼MN后有一个小山坡AC,其坡度为i=1:2.4(注:坡度是指坡面的铅直高度与水平宽度的比),小区准备在小山坡上加装广告牌PQ.已知广告牌底端Q到坡底A的距离为5.2米,水平地面上居民楼MN到坡底A的距离为1.2米,当太阳光线与水平线成53°角时,测得广告牌PQ落在居民楼上的影子DN长为3米.则广告牌PQ的高为 9米 .(参考数据:)
16. 如图,在平面直角坐标系xOy中,点A在x轴负半轴上,点B在y轴正半轴上,⊙D经过A,B,O,C四点,,,则圆心点D的坐标是
三、解答题(共72分)
17.(8分)已知不等式的最小整数解是方程的解,求a的值.
不等式解集:; 最小整数解:;
18.(8分)先化简:,再在不等式组的整数解中取一个合适的代入求值.
化简为 ; 不等式组的解集为; a可以取0或1不能取2
19.(8分)如图所示,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD
(1)证明:BD=CD; (2)当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.
(1)略 (2)当△ABC满足:AB=AC时,四边形AFBD是矩形,
20.(8分)中华文化源远流长,文学方面,《西游记》《三国演义》《水浒传》《红楼梦》是我国古代长篇小说中的典型代表,就“四大古典名著你读完了几部”的问题在全校学生中进行了抽样调查,根据调查结果绘制成如下尚不完整的统计图.
请根据以上信息,解决下列问题
(1)本次调查所得数据的众数是 部,中位数是 部;
(2)扇形统计图中“4部”所在扇形的圆心角为 度;
(3)请将条形统计图补充完整;
(4)没有读过四大古典名著的两名学生准备从中各自随机选择一部来阅读,求他们恰好选中同一名著的概率.
(1)答案为:1、2;(2)答案为:54;
(3)条形统计图如图所示,
(4)P(两人选中同一名著)==
21.(8分)如图,已知⊙O经过菱形ABCD的顶点A,C,且与CD相切,直径CF交AB于点E.
(1)求证:AD与⊙O相切;(2)若,求的值.
(1)略, (2)
22.(10分)“冰墩墩”和“雪容融”作为北京冬奥会和残奥会的吉祥物深受大家喜爱,某旗舰店销售“冰墩墩”毛绒玩具总额为24000元,销售“雪容融”毛绒玩具总额为8000元,其中“冰墩墩”的销售单价比“雪容融”的销售单价多40元,并且销售“冰墩墩”的数量是“雪容融”数量的2倍.
(1)求“冰墩墩”和“雪容融”的销售单价分别是多少元?
(2)已知“冰墩墩”和“雪容融”的成本分别为100元/个和60元/个,进入2022年1月后,这两款毛绒玩具持续热销,于是该旗舰店再购进了这两款毛绒玩具共800个,其中“雪容融”的数量不超过“冰墩墩”数量的3倍,且这两款毛绒玩具购进总价不超过57600元.为回馈新老客户,该旗舰店决定对“冰墩墩”降价10%后再销售,若1月份购进的这两款毛绒玩具全部售出,则“冰墩墩”购进多少个时该旗舰店当月销售利润最大,并求出最大利润.
(1) “冰墩墩”的销售单价是120元,“雪容融”的销售单价是80元;
(2)冰墩墩”购进200个时,该旗舰店当月销售利润最大,最大利润为13600元.
23.(10分)在Rt△ABC,∠C=90°,D为AB边上一点,点M、N分别在BC、AC边上,且DM⊥DN.作MF⊥AB于点F,NE⊥AB于点E.
(1)特殊验证:如图1,若AC=BC,且D为AB中点,求证:DM=DN,AE=DF;
(2)拓展探究:若AC≠BC.
①如图2,若D为AB中点,(1)中的两个结论有一个仍成立,请指出并加以证明;
②如图3,若BD=kAD,条件中“点M在BC边上”改为“点M在线段CB的延长线上”,其它条件不变,请探究AE与DF的数量关系并加以证明.
(1)略 (2)①AE=DF. ②DF=kAE.
24.(12分)已知抛物线与x轴负半轴交于点A,与x轴正半轴交于点B,与y轴交于点C,且.直线与抛物线交于D,E两点(点D在点E的左侧),连接OD,OE.
(1)求抛物线的解析式;
(2)若的面积为,求k的值;
(3)求证:不论k取何值,抛物线上都存在定点F,使得是以DE为斜边的直角三角形.
(1)抛物线的解析式为.
(2)
(3)抛物线上存在定点,使得是以DE为斜边的直角三角形.
姓名 分数
一、选择题(每小题3分,共30分)
1. 下列各数中与2互为相反数的是( )
A. B. C. D.
2. 已知:点P(3-m,m-1)关于x轴对称的点在第三象限,则m的取值范围在数轴上表示正确的是( )
3. 某市为了方便市民绿色出行,推出了共享单车服务.图①是某品牌共享单车放在水平地面的实物图,图②是其示意图,其中AB,CD都与地面l平行,∠BCD=60°,∠BAC=54°.当∠MAC为( )度时,AM与CB平行.
A.16 B.60 C.66 D.114
4. 下列各式中无意义的是( )
A. B. C. D.
5. 为选拔一位同学参加校运会50米跑项目,九(1)班班委对甲,乙,丙,丁4位同学进行了50米跑的多次测试,现将四位同学的测试数据整理在表格中,则应该选择( )参加比赛.
甲 乙 丙 丁
平均用时/秒 8.2 7.9 7.9 8.2
方差 2.2 1.4 2.4 1.4
A.甲 B.乙 C.丙 D.丁
6. 如图,有一池塘,要测池塘两端A,B的距离,可先在地上取一个点C,从点C不经过池塘可以直接到达点A和B.连接AC并延长到点D,使CD=CA.连接BC并延长到点E,使CE=CB.连接DE,根据两个三角形全等,那么量出DE的长就知道A、B的距离.判断图中两个三角形全等的依据是( )
A.SAS B.SSS C.ASA D.AAS
7. 我国古代数学名著《四元玉鉴》中记载:“九百九十九文钱,及时梨果买一千,一十一文梨九个,七枚果子四文钱.问梨果各几何?”意思是:用999文钱买得梨和果共1000个,梨11文买9个,果4文买7个,问梨果各买了多少个?如果设梨买x个,果买y个,那么可列方程组为( )
A. B. C. D.
8. 佳佳和爸爸一起从家出发,匀速行走25min后抵达离家1000m的报亭,佳佳随即按原速返回,爸爸看了10min报后返回,恰好与佳佳同时到家.则表示爸爸离家后距离与时间关系的大致图象是( )
A. B. C. D.
9. 如图所示,在△ABC中,BC=3,AC=4,∠ACB=90°,以点B为圆心,BC长为半径画弧,与AB交于点D,再分别以A、D为圆心,大于的长为半径画弧,两弧交于点E、F,作直线EF,分别交AC、AB于点P、Q,则PQ的长度为( )
A. B. C. D.
10. 如图,在直角坐标系中,Rt△OAB的边OB在y轴上,∠ABO=90°,AB=3,点C在AB上,BC=AB,且∠BOC=∠A,若双曲线y=经过点C,则k的值为( )
A. B. C.1 D.2
二、填空题(每小题3分,共18分
11. 分别写出数字、、、的四张卡片中,除数字外其他均相同,从中随机抽取一张是无理数的概率是 .
12. 如图,三角形ABC中,∠ACB=90°,AC=6,BC=8,P为直线AB上一动点,连PC,则线段PC的最小值是 .
13. 设m,n是方程的两个实数根,则的值为______.
14. 如图是一个正方体的展开图,将它折叠成正方体后,“数”字的对面上的文字是
15. 如图,某居民楼MN后有一个小山坡AC,其坡度为i=1:2.4(注:坡度是指坡面的铅直高度与水平宽度的比),小区准备在小山坡上加装广告牌PQ.已知广告牌底端Q到坡底A的距离为5.2米,水平地面上居民楼MN到坡底A的距离为1.2米,当太阳光线与水平线成53°角时,测得广告牌PQ落在居民楼上的影子DN长为3米.则广告牌PQ的高为 .(参考数据:)
16. 如图,在平面直角坐标系xOy中,点A在x轴负半轴上,点B在y轴正半轴上,⊙D经过A,B,O,C四点,,,则圆心点D的坐标是
三、解答题(共72分)
17.(8分)已知不等式的最小整数解是方程的解,求a的值.
18.(8分)先化简:,再在不等式组的整数解中取一个合适的代入求值.
19.(8分)如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD.
(1)证明:BD=CD; (2)当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.
20.(8分)中华文化源远流长,文学方面,《西游记》《三国演义》《水浒传》《红楼梦》是我国古代长篇小说中的典型代表,就“四大古典名著你读完了几部”的问题在全校学生中进行了抽样调查,根据调查结果绘制成如下尚不完整的统计图.
请根据以上信息,解决下列问题
(1)本次调查所得数据的众数是 部,中位数是 部;
(2)扇形统计图中“4部”所在扇形的圆心角为 度;
(3)请将条形统计图补充完整;
(4)没有读过四大古典名著的两名学生准备从中各自随机选择一部来阅读,求他们恰好选中同一名著的概率.
21.(8分)如图,已知⊙O经过菱形ABCD的顶点A,C,且与CD相切,直径CF交AB于点E.
(1)求证:AD与⊙O相切;(2)若,求的值.
22.(10分)“冰墩墩”和“雪容融”作为北京冬奥会和残奥会的吉祥物深受大家喜爱,某旗舰店销售“冰墩墩”毛绒玩具总额为24000元,销售“雪容融”毛绒玩具总额为8000元,其中“冰墩墩”的销售单价比“雪容融”的销售单价多40元,并且销售“冰墩墩”的数量是“雪容融”数量的2倍.
(1)求“冰墩墩”和“雪容融”的销售单价分别是多少元?
(2)已知“冰墩墩”和“雪容融”的成本分别为100元/个和60元/个,进入2022年1月后,这两款毛绒玩具持续热销,于是该旗舰店再购进了这两款毛绒玩具共800个,其中“雪容融”的数量不超过“冰墩墩”数量的3倍,且这两款毛绒玩具购进总价不超过57600元.为回馈新老客户,该旗舰店决定对“冰墩墩”降价10%后再销售,若1月份购进的这两款毛绒玩具全部售出,则“冰墩墩”购进多少个时该旗舰店当月销售利润最大,并求出最大利润.
23.(10分)在Rt△ABC,∠C=90°,D为AB边上一点,点M、N分别在BC、AC边上,且DM⊥DN.作MF⊥AB于点F,NE⊥AB于点E.
(1)特殊验证:如图1,若AC=BC,且D为AB中点,求证:DM=DN,AE=DF;
(2)拓展探究:若AC≠BC.
①如图2,若D为AB中点,(1)中的两个结论有一个仍成立,请指出并加以证明;
②如图3,若BD=kAD,条件中“点M在BC边上”改为“点M在线段CB的延长线上”,其它条件不变,请探究AE与DF的数量关系并加以证明.
24.(12分)已知抛物线与x轴负半轴交于点A,与x轴正半轴交于点B,与y轴交于点C,且.直线与抛物线交于D,E两点(点D在点E的左侧),连接OD,OE.
(1)求抛物线的解析式;
(2)若的面积为,求k的值;
(3)求证:不论k取何值,抛物线上都存在定点F,使得是以DE为斜边的直角三角形.
2023年荆州中考数学综合练习题
姓名 分数
一、选择题(每小题3分,共30分)
1. 下列各数中与2互为相反数的是( D )
A. B. C. D.
2. 已知:点P(3-m,m-1)关于x轴对称的点在第三象限,则m的取值范围在数轴上表示正确的是( A )
3. 某市为了方便市民绿色出行,推出了共享单车服务.图①是某品牌共享单车放在水平地面的实物图,图②是其示意图,其中AB,CD都与地面l平行,∠BCD=60°,∠BAC=54°.当∠MAC为( C )度时,AM与CB平行.
A.16 B.60 C.66 D.114
4. 下列各式中无意义的是( D )
A. B. C. D.
5. 为选拔一位同学参加校运会50米跑项目,九(1)班班委对甲,乙,丙,丁4位同学进行了50米跑的多次测试,现将四位同学的测试数据整理在表格中,则应该选择( B )参加比赛.
甲 乙 丙 丁
平均用时/秒 8.2 7.9 7.9 8.2
方差 2.2 1.4 2.4 1.4
A.甲 B.乙 C.丙 D.丁
6. 如图,有一池塘,要测池塘两端A,B的距离,可先在地上取一个点C,从点C不经过池塘可以直接到达点A和B.连接AC并延长到点D,使CD=CA.连接BC并延长到点E,使CE=CB.连接DE,根据两个三角形全等,那么量出DE的长就知道A、B的距离.判断图中两个三角形全等的依据是( A )
A.SAS B.SSS C.ASA D.AAS
7. 我国古代数学名著《四元玉鉴》中记载:“九百九十九文钱,及时梨果买一千,一十一文梨九个,七枚果子四文钱.问梨果各几何?”意思是:用999文钱买得梨和果共1000个,梨11文买9个,果4文买7个,问梨果各买了多少个?如果设梨买x个,果买y个,那么可列方程组为( A )
A. B. C. D.
8. 佳佳和爸爸一起从家出发,匀速行走25min后抵达离家1000m的报亭,佳佳随即按原速返回,爸爸看了10min报后返回,恰好与佳佳同时到家.则表示爸爸离家后距离与时间关系的大致图象是( B )
A. B. C. D.
9. 如图所示,在△ABC中,BC=3,AC=4,∠ACB=90°,以点B为圆心,BC长为半径画弧,与AB交于点D,再分别以A、D为圆心,大于的长为半径画弧,两弧交于点E、F,作直线EF,分别交AC、AB于点P、Q,则PQ的长度为( B )
A. B. C. D.
10. 如图,在直角坐标系中,Rt△OAB的边OB在y轴上,∠ABO=90°,AB=3,点C在AB上,BC=AB,且∠BOC=∠A,若双曲线y=经过点C,则k的值为( B )
A. B. C.1 D.2
二、填空题(每小题3分,共18分
11. 分别写出数字、、、的四张卡片中,除数字外其他均相同,从中随机抽取一张是无理数的概率是____.
12. 如图,三角形ABC中,∠ACB=90°,AC=6,BC=8,P为直线AB上一动点,连PC,则线段PC的最小值是 .
13. 设m,n是方程的两个实数根,则的值为___-1___.
14. 如图是一个正方体的展开图,将它折叠成正方体后,“数”字的对面上的文字是 试
15. 如图,某居民楼MN后有一个小山坡AC,其坡度为i=1:2.4(注:坡度是指坡面的铅直高度与水平宽度的比),小区准备在小山坡上加装广告牌PQ.已知广告牌底端Q到坡底A的距离为5.2米,水平地面上居民楼MN到坡底A的距离为1.2米,当太阳光线与水平线成53°角时,测得广告牌PQ落在居民楼上的影子DN长为3米.则广告牌PQ的高为 9米 .(参考数据:)
16. 如图,在平面直角坐标系xOy中,点A在x轴负半轴上,点B在y轴正半轴上,⊙D经过A,B,O,C四点,,,则圆心点D的坐标是
三、解答题(共72分)
17.(8分)已知不等式的最小整数解是方程的解,求a的值.
不等式解集:; 最小整数解:;
18.(8分)先化简:,再在不等式组的整数解中取一个合适的代入求值.
化简为 ; 不等式组的解集为; a可以取0或1不能取2
19.(8分)如图所示,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD
(1)证明:BD=CD; (2)当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.
(1)略 (2)当△ABC满足:AB=AC时,四边形AFBD是矩形,
20.(8分)中华文化源远流长,文学方面,《西游记》《三国演义》《水浒传》《红楼梦》是我国古代长篇小说中的典型代表,就“四大古典名著你读完了几部”的问题在全校学生中进行了抽样调查,根据调查结果绘制成如下尚不完整的统计图.
请根据以上信息,解决下列问题
(1)本次调查所得数据的众数是 部,中位数是 部;
(2)扇形统计图中“4部”所在扇形的圆心角为 度;
(3)请将条形统计图补充完整;
(4)没有读过四大古典名著的两名学生准备从中各自随机选择一部来阅读,求他们恰好选中同一名著的概率.
(1)答案为:1、2;(2)答案为:54;
(3)条形统计图如图所示,
(4)P(两人选中同一名著)==
21.(8分)如图,已知⊙O经过菱形ABCD的顶点A,C,且与CD相切,直径CF交AB于点E.
(1)求证:AD与⊙O相切;(2)若,求的值.
(1)略, (2)
22.(10分)“冰墩墩”和“雪容融”作为北京冬奥会和残奥会的吉祥物深受大家喜爱,某旗舰店销售“冰墩墩”毛绒玩具总额为24000元,销售“雪容融”毛绒玩具总额为8000元,其中“冰墩墩”的销售单价比“雪容融”的销售单价多40元,并且销售“冰墩墩”的数量是“雪容融”数量的2倍.
(1)求“冰墩墩”和“雪容融”的销售单价分别是多少元?
(2)已知“冰墩墩”和“雪容融”的成本分别为100元/个和60元/个,进入2022年1月后,这两款毛绒玩具持续热销,于是该旗舰店再购进了这两款毛绒玩具共800个,其中“雪容融”的数量不超过“冰墩墩”数量的3倍,且这两款毛绒玩具购进总价不超过57600元.为回馈新老客户,该旗舰店决定对“冰墩墩”降价10%后再销售,若1月份购进的这两款毛绒玩具全部售出,则“冰墩墩”购进多少个时该旗舰店当月销售利润最大,并求出最大利润.
(1) “冰墩墩”的销售单价是120元,“雪容融”的销售单价是80元;
(2)冰墩墩”购进200个时,该旗舰店当月销售利润最大,最大利润为13600元.
23.(10分)在Rt△ABC,∠C=90°,D为AB边上一点,点M、N分别在BC、AC边上,且DM⊥DN.作MF⊥AB于点F,NE⊥AB于点E.
(1)特殊验证:如图1,若AC=BC,且D为AB中点,求证:DM=DN,AE=DF;
(2)拓展探究:若AC≠BC.
①如图2,若D为AB中点,(1)中的两个结论有一个仍成立,请指出并加以证明;
②如图3,若BD=kAD,条件中“点M在BC边上”改为“点M在线段CB的延长线上”,其它条件不变,请探究AE与DF的数量关系并加以证明.
(1)略 (2)①AE=DF. ②DF=kAE.
24.(12分)已知抛物线与x轴负半轴交于点A,与x轴正半轴交于点B,与y轴交于点C,且.直线与抛物线交于D,E两点(点D在点E的左侧),连接OD,OE.
(1)求抛物线的解析式;
(2)若的面积为,求k的值;
(3)求证:不论k取何值,抛物线上都存在定点F,使得是以DE为斜边的直角三角形.
(1)抛物线的解析式为.
(2)
(3)抛物线上存在定点,使得是以DE为斜边的直角三角形.
同课章节目录
