类比推理[上学期]
图片预览





文档简介
课件19张PPT。【合情推理】
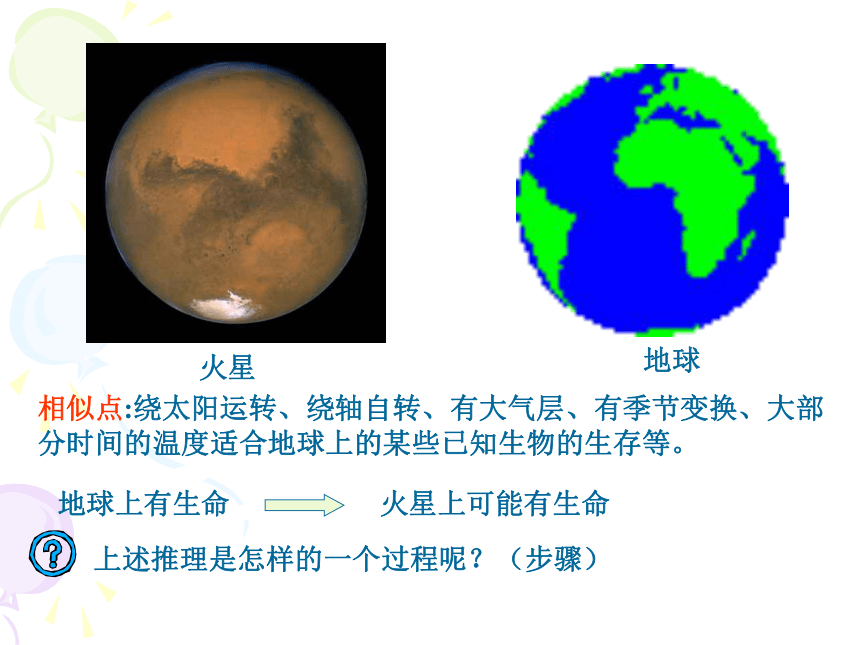
_____类比推理执教教师:潮阳一中 常春红相似点:绕太阳运转、绕轴自转、有大气层、有季节变换、大部
分时间的温度适合地球上的某些已知生物的生存等。地球上有生命火星上可能有生命上述推理是怎样的一个过程呢?(步骤)火星上有没有生命?可能有生命存在有生命存在大部分时间的温度适合地球上某些已知生物的生存温度适合生物的生存一年中有四季的变更一年中有四季的变更有大气层有大气层行星、围绕太阳运行、绕轴自转行星、围绕太阳运行、绕轴自转火 星 地 球类比推理定义:由两类对象具有某些类似特征和其中一类对象的某些已知特征,推出另一类对象也具有这些特征的推理称为类比推理(简称类比)。特点 :
1、类比是从人们已经掌握的事物的属性,推断正在研究中的事物的属性,它以旧有知识为基础,类比出新的结论。 2、是从一事物的特殊属性推断另一种事物的特殊属性。3、类比的结果具有猜测性4、类比推理是由特殊到特殊的推理例如:进行类比推理的步骤:
(1)找出两类对象之间可以确切表述的相似特征;
(2)用一类对象的已知特征去猜测另一类对象的特征,
从而得出一个猜想;
(3)检验这个猜想. 三角形面积公式圆的面积公式
↓升维 ↓升维
球的体积公式棱锥体积公式以直代曲以直代曲类比推理在立体几何中的应用类比的前提:相似性类比的方法:进行相
似性变换,留同增异由平面向空间类比的
方向:由低维推向高维 数学思想方法: 类比 以直代曲 特殊化解题思维过程:
类比,猜测,论证 研究对象:点线面位置关系:线线线面度量关系:长度面积数量形式:数轴平面直角坐标空间直角坐标体 面面 体积 1.半径为r的圆的面积S(r)= ,周长C(r)=
,若将r看作(0,+∞)上的变量,则
①,
①式可以用语言叙述为:圆的面积函数的导数等于圆的周长函数。
类比:对于半径为R的球,若将R看作(0,+∞)上的变量,请你写出类似于①的式子:
②
②式可以用语言叙述为:
__________________________________________球的体积函数的导数等于球的面积函数2.定理:在平面内,垂直于同一直线的两条直线互相平行.
类比:在空间中, .猜想:(1)在空间中,垂直于同一平面的两条直线互相平行;(2)在空间中,垂直于同一直线的两个平面互相平行;(3)在空间中,垂直于同一平面的两个平面互相平行;3.有对称中心的曲线叫做有心曲线,显然椭圆、双曲线都是有心曲线.过有心圆锥曲线中心的弦叫有心圆锥曲线的直径。
定理:过圆 上异于直径两端点的任意一点与一条直径的两个端点连线,则两条连线所在直线的斜率之积为定值-1.
(1)写出定理在椭圆 中的推广,并加以证明;
(2)写出定理在双曲线 中的推广;你能从上述结论中得到有心圆锥曲线(包括椭圆、双曲线、圆)的一般性结论吗?请写出你的结论。?3.有对称中心的曲线叫做有心曲线,显然椭圆、双曲线都是有心曲线.过有心圆锥曲线中心的弦叫有心圆锥曲线的直径。
定理:过圆 上异于直径两端点的任意一点与一条直径的两端点连线,则两条连线所在直线的斜率之积为定值-1.
(1)过椭圆 上异于直径两端点的任意一点与一条直径的两个端点连线,则两条连线所在直线的斜率之积的
定值为 ;4.当 成等差数列时,有 ;
当 成等差数列时,有 ;
当 成等差数列时,有
由此归纳:当 成等差数列时有
如果 成等比数列,类比上述方法归纳出的等式为 。
6.由上图(左)有面积关系: 则由上图(右),有体积关系: ________________ 1、运用类比方法解决问题,其基本过程可用框图
表示如下:小 结:原问题类比问题原问题解法类比问题的解法2、运用类比法的关键是:寻找一个合适的类比对象。 谢谢 !!!
_____类比推理执教教师:潮阳一中 常春红相似点:绕太阳运转、绕轴自转、有大气层、有季节变换、大部
分时间的温度适合地球上的某些已知生物的生存等。地球上有生命火星上可能有生命上述推理是怎样的一个过程呢?(步骤)火星上有没有生命?可能有生命存在有生命存在大部分时间的温度适合地球上某些已知生物的生存温度适合生物的生存一年中有四季的变更一年中有四季的变更有大气层有大气层行星、围绕太阳运行、绕轴自转行星、围绕太阳运行、绕轴自转火 星 地 球类比推理定义:由两类对象具有某些类似特征和其中一类对象的某些已知特征,推出另一类对象也具有这些特征的推理称为类比推理(简称类比)。特点 :
1、类比是从人们已经掌握的事物的属性,推断正在研究中的事物的属性,它以旧有知识为基础,类比出新的结论。 2、是从一事物的特殊属性推断另一种事物的特殊属性。3、类比的结果具有猜测性4、类比推理是由特殊到特殊的推理例如:进行类比推理的步骤:
(1)找出两类对象之间可以确切表述的相似特征;
(2)用一类对象的已知特征去猜测另一类对象的特征,
从而得出一个猜想;
(3)检验这个猜想. 三角形面积公式圆的面积公式
↓升维 ↓升维
球的体积公式棱锥体积公式以直代曲以直代曲类比推理在立体几何中的应用类比的前提:相似性类比的方法:进行相
似性变换,留同增异由平面向空间类比的
方向:由低维推向高维 数学思想方法: 类比 以直代曲 特殊化解题思维过程:
类比,猜测,论证 研究对象:点线面位置关系:线线线面度量关系:长度面积数量形式:数轴平面直角坐标空间直角坐标体 面面 体积 1.半径为r的圆的面积S(r)= ,周长C(r)=
,若将r看作(0,+∞)上的变量,则
①,
①式可以用语言叙述为:圆的面积函数的导数等于圆的周长函数。
类比:对于半径为R的球,若将R看作(0,+∞)上的变量,请你写出类似于①的式子:
②
②式可以用语言叙述为:
__________________________________________球的体积函数的导数等于球的面积函数2.定理:在平面内,垂直于同一直线的两条直线互相平行.
类比:在空间中, .猜想:(1)在空间中,垂直于同一平面的两条直线互相平行;(2)在空间中,垂直于同一直线的两个平面互相平行;(3)在空间中,垂直于同一平面的两个平面互相平行;3.有对称中心的曲线叫做有心曲线,显然椭圆、双曲线都是有心曲线.过有心圆锥曲线中心的弦叫有心圆锥曲线的直径。
定理:过圆 上异于直径两端点的任意一点与一条直径的两个端点连线,则两条连线所在直线的斜率之积为定值-1.
(1)写出定理在椭圆 中的推广,并加以证明;
(2)写出定理在双曲线 中的推广;你能从上述结论中得到有心圆锥曲线(包括椭圆、双曲线、圆)的一般性结论吗?请写出你的结论。?3.有对称中心的曲线叫做有心曲线,显然椭圆、双曲线都是有心曲线.过有心圆锥曲线中心的弦叫有心圆锥曲线的直径。
定理:过圆 上异于直径两端点的任意一点与一条直径的两端点连线,则两条连线所在直线的斜率之积为定值-1.
(1)过椭圆 上异于直径两端点的任意一点与一条直径的两个端点连线,则两条连线所在直线的斜率之积的
定值为 ;4.当 成等差数列时,有 ;
当 成等差数列时,有 ;
当 成等差数列时,有
由此归纳:当 成等差数列时有
如果 成等比数列,类比上述方法归纳出的等式为 。
6.由上图(左)有面积关系: 则由上图(右),有体积关系: ________________ 1、运用类比方法解决问题,其基本过程可用框图
表示如下:小 结:原问题类比问题原问题解法类比问题的解法2、运用类比法的关键是:寻找一个合适的类比对象。 谢谢 !!!
