七年级数学上册《1.3.1 有理数的加法》教学设计 新人教版
文档属性
| 名称 | 七年级数学上册《1.3.1 有理数的加法》教学设计 新人教版 |  | |
| 格式 | zip | ||
| 文件大小 | 49.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-08-29 17:22:40 | ||
图片预览


文档简介
有理数的加法
一、内容及其分析
本节课要学的内容是有理数加法,指的是求两个有理数的和,其核心是怎样求几个有理数的和,理解它的关键就是弄清求和的几种形式。学生已经学过小学数的加法,本节课的内容有理数加法就是在此基础上的发展,就可以类比它。由于它还与有理数的减法有必然的联系,所以在本学科有非常重要的地位,并且是本章的基础,是本学科的核心内容。教学的重点是有理数加法法则的理解和运用,如何运用加法运算律简化运算,解决重点的关键是用图解或分类的方法。
二、目标及其解析
1、目标定位:了解有理数加法的意义;理解有理数加法的法则;能根据有理数加法法则熟练地进行有理数加法运算.能运用加法运算律简化加法运算.
2、目标解析:了解有理数加法的意义就是指在实际问题中探究出有理数的加法表达的意义的基础上,得到有理数加法的一般法则。
三、问题诊断与分析
在本节课的教学中,学生可能遇到的问题是和的符合不知道怎样判断,产生这一问题的原因是与小学加法没有符号的判断。要解决这一问题就要学生通过具体的训练找到符号判断的规律,其中关键是对不同形式的。
四、教学支持条件分析
五、教学过程设计:
(一)创设情景,引入本节要研究的问题
问题1:“我从学校出发沿某条路向东走米,再继续向东走米,那么两次我一共向东走了多少米?”
设计意图:
让学生通过实例明确有理数加法的实际意义,明白同一性质的有理数的加法的实际意义。
师生活动:
(1)小王第一次向东走了5m,再向东走了3 m,他向东一共走了多少米?
(2)若都表示有理数,这显然是求两数( )的问题;
(3)怎样求a、b的和呢?
变式练习:
(1)我从教室向餐厅走了20米到旗杆下,再向餐厅走了21米到商店,一共走了多少米?
(二)探索新知,主体探究,导出法则
问题2:既然均是有理数,它们可能是正数,也可能是负数或者零.同学思考一下:的符号可能有几种情况?
设计意图:这种分类让基础差的同学能找到规律,从而解决类似的有理数加法。
师生活动:
根据所学过的数的情况,容易想到有以下几种情况:
(1)同为正数(2)同为负数(3)一个正数一个负数(4)加数中有一个是0;下面我们就来研究这几种情况下有理数的加法问题.在研究之前,首先提醒同学注意正确理解“向东走米”的含义.为了研究的方便起见,用数轴来帮助我们,并设向东为正.
变式练习:
问题3:请你分别把a、b赋予不同情况的有理数,然后进行加法运算,你会有什么样的结论?你能发现有理数的加法法则吗?
设计意图:从特殊到一般让学生更加理解有理数加法的意义
师生活动:
(1)同桌小组合作,主体探究,自主归纳;
(2)学生经过思考,可能会有以下结果(若没有讨论完整教师作适当提示).
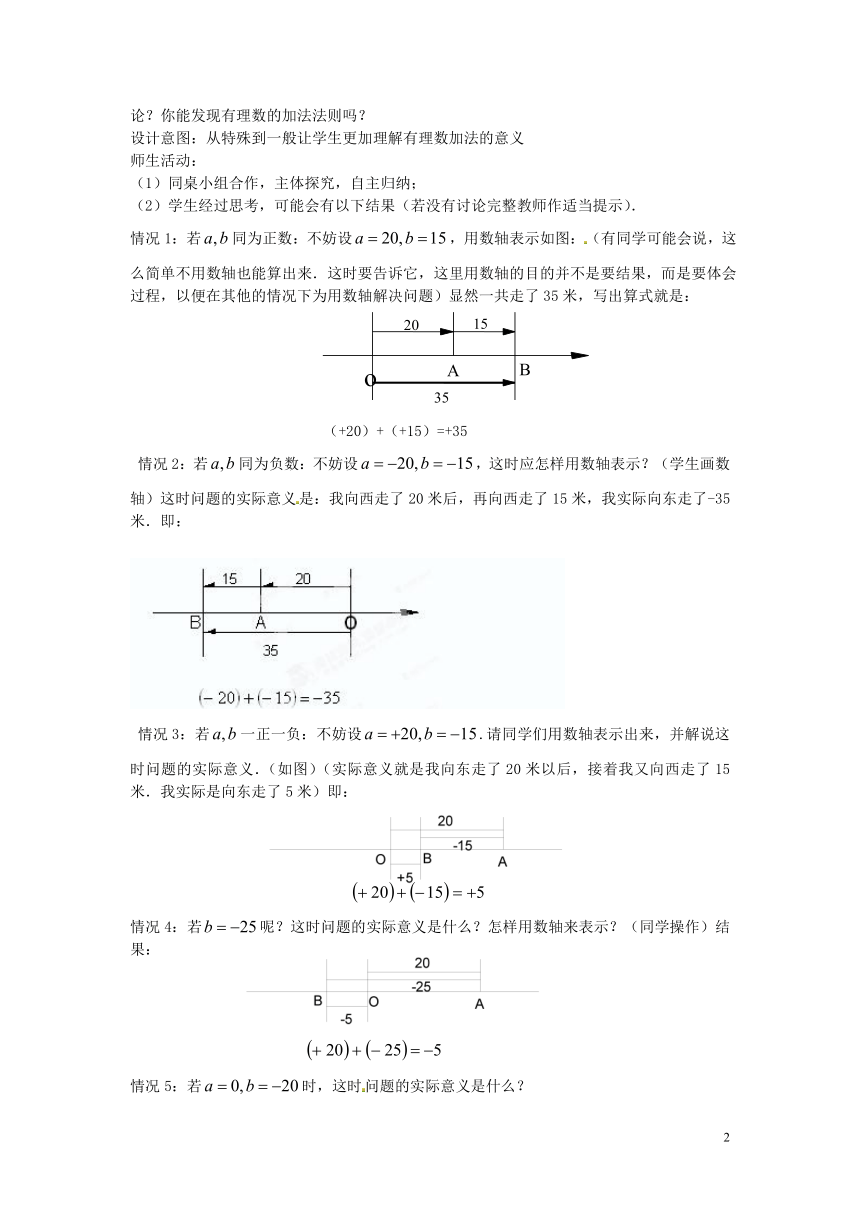
情况1:若同为正数:不妨设,用数轴表示如图:(有同学可能会说,这么简单不用数轴也能算出来.这时要告诉它,这里用数轴的目的并不是要结果,而是要体会过程,以便在其他的情况下为用数轴解决问题)显然一共走了35米,写出算式就是:
(+20)+(+15)=+35
情况2:若同为负数:不妨设,这时应怎样用数轴表示?(学生画数轴)这时问题的实际意义是:我向西走了20米后,再向西走了15米,我实际向东走了-35米.即:
情况3:若一正一负:不妨设.请同学们用数轴表示出来,并解说这时问题的实际意义.(如图)(实际意义就是我向东走了20米以后,接着我又向西走了15米.我实际是向东走了5米)即:
情况4:若呢?这时问题的实际意义是什么?怎样用数轴来表示?(同学操作)结果:
情况5:若时,这时问题的实际意义是什么?
结果:
情况6:若时,这时问题的实际意义又是什么?
结果:
情况7:若时,这时问题的实际意义是什么?
结果:
情况8:若时,这时问题的实际意义是什么?
结果:
综合以上几种情况,得到8个式子,我们将这8个式子分成同号、异号、有零的三种情况统计如下:
(1)同号的情况:; .
(2)异号的情况:; ;
; .
(3)有零的情况:; .
同学归纳有理数的加法法则,若归纳不完整,则有其他同学进行补充,直到法则完善化,必要时教师进行点拨:
有理数加法法则
1、同号两数相加,取相同的符号,并把绝对值相加;2、异号两数相加时: (1)若绝对值不相等,取绝对值较大加数的符号,并用较大的绝对值减去较小的绝对值; (2)若绝对值相等,和为0. 也就是相反数的和为0;3、一个数与0的和仍得这个数.
变式练习:
计算:(先口述运用法则的过程,然后说出计算结果)从计算的过程看,你有什么发现?
(1);(2); (3);(4);
(5); (6); (7); (8).
归纳:进行加法运算时首先判断关系、其次确定符号、最后计算绝对值.
三、法则应用、主体反馈
问题4:计算下列各题:
(1) ; (2); (3);
(4); (5).
设计意图:让学生独立完成,在完成的过程中可以让学生进行板演,然后再共同分析过程的正确性,在分析过程的正确性时要充分发挥学生的主体性,让学生充分发表自己的看法,最后得到统一的正确的结论,这样让学生更深刻的理解有理数的加法的意义.
师生活动:
变式练习:
(1) ; (2); (3);
(4); (5).
四、体验探索、发现运算率
问题5: 解决下列问题:
体验1:请你任意取两个有理数(至少有一个是负数),填入下列□和○中,比较它们的运算结果,你能发现什么?
□+○ ○+□
师生活动:
学生独立完成这项任务,自己寻找自己认为合适的有理数,经过运算,可以发现:对任意的两个有理数都有□+○=○+□,即:小学里学的加法交换律在有理数范围内仍成立
体验2:请你任意取三个有理数(至少有一个是负数),填入下列□、○和◇中,比较它们的运算结果,你能发现什么?
(□+○)+◇ □+(○+◇)
师生活动:
学生独立完成这项任务,自己寻找自己认为合适的有理数,经过运算,可以发现:对任意的两个有理数都有(□+○)+◇=□+(○+◇),即:小学里学的加法结合律在有理数范围内仍成立,即:a+b=b+a,(a+b)+c=a+(b+c).
五、应用迁移、巩固提高
问题6: 解决下列问题.
1.计算下列各式.
(1) ;
(2);
(3);
(4)1+(-2)+3+(-4)+……+2005+(-2006).
师生活动:
1、学生独立思考,完成对上述问题的解决,在解决的过程中可能有不同的方法,出现时可以让学生比较各种方法间的异同、优劣,以找到最佳方法,体会运算律的作用.
(1)中运用运算律可以先把正数相加,再把负数相加,然后再把结果相加即可;(2)中运用运算律可以先把第一项和第三项相加、第二项与第四项相加;
(3)运用运算律先把前三项相加、后两项相加;
(4)运用结合律把2006个加数分成1003组,分别相加.
归纳:运算律可以使运算简便(原因是它改变了运算顺序)
2.工地上运来20袋水泥,过秤的结果如下表(单位:千克)
袋号 1 2 3 4 5 6 7 8 9 10
重量 201 204 199 197 203 200 201 202 198 197
袋号 11 12 13 14 15 16 17 18 19 20
重量 196 172 198 203 200 202 201 199 197 205
已知每袋的额定重量为200千克,这批水泥总重量的误差总量是多少千克?
师生活动:
第一步:列出误差表(单位:千克)
袋号 1 2 3 4 5 6 7 8 9 10
误差值 1 4 -1 -3 3 0 1 2 -2 -3
袋号 11 12 13 14 15 16 17 18 19 20
误差值 -4 -28 -2 3 0 2 1 -1 -3 5
注意观察误差值有无互为相反数?所以实际误差总值是袋号7、12、19、20的误差值的和:
=
于是误差总量是不足25千克.
3.一只乌龟沿南北方向的河岸来回爬行,假定向北爬行的路程记为正数,向南爬行的路程记为负数,它爬行的过程记录如下(单位m):-8,7,-3,9,-6,-4,10.
(1) 乌龟最后距离出发点多远,在出发点的南边还是北边;
(2) 求乌龟在整个过程中一共爬行了多远的距离.
师生活动:
学生思考,这个问题可以运用什么知识,由于
(1)求的是乌龟最后距离改为的位置与出发点的距离改为关系,因此可以把上述过程记录加起来,看运算结果即可;
(2)求的是一共爬行的路程,因此把上述过程记录取绝对值后再加起来就行了.
(1)-8+7-3+9-6-4+10=5,所以在出发点的北边;
(2)|-8|+7+|-3|+|9|+|-6|+|-4|+10=47;
所以乌龟在整个过程中一共爬行了47米.
六、课堂小结
1.加法法则(主要是异号两数相加);
2.加法运算律.
七、目标检测:
1、计算:(先口述运用法则的过程,然后说出计算结果)从计算的过程看,你有什么发现?
(1);(2); (3);(4);
(5); (6); (7); (8).
2、计算下列各题:
(1) ; (2); (3);
(4); (5).
八、配餐练习
A组:基础巩固: 习题1、2、3题
B组:强化训练
第1、2题,
(2) ;
(3)
C组:延伸拓广
(1) 第7、8、9、10题;
(2)1+(-2)+3+(-4)+……+2005+(-2006)+2007+(-2008)+2009+(-2010)=___________
o
B
A
20
15
35
PAGE
1
一、内容及其分析
本节课要学的内容是有理数加法,指的是求两个有理数的和,其核心是怎样求几个有理数的和,理解它的关键就是弄清求和的几种形式。学生已经学过小学数的加法,本节课的内容有理数加法就是在此基础上的发展,就可以类比它。由于它还与有理数的减法有必然的联系,所以在本学科有非常重要的地位,并且是本章的基础,是本学科的核心内容。教学的重点是有理数加法法则的理解和运用,如何运用加法运算律简化运算,解决重点的关键是用图解或分类的方法。
二、目标及其解析
1、目标定位:了解有理数加法的意义;理解有理数加法的法则;能根据有理数加法法则熟练地进行有理数加法运算.能运用加法运算律简化加法运算.
2、目标解析:了解有理数加法的意义就是指在实际问题中探究出有理数的加法表达的意义的基础上,得到有理数加法的一般法则。
三、问题诊断与分析
在本节课的教学中,学生可能遇到的问题是和的符合不知道怎样判断,产生这一问题的原因是与小学加法没有符号的判断。要解决这一问题就要学生通过具体的训练找到符号判断的规律,其中关键是对不同形式的。
四、教学支持条件分析
五、教学过程设计:
(一)创设情景,引入本节要研究的问题
问题1:“我从学校出发沿某条路向东走米,再继续向东走米,那么两次我一共向东走了多少米?”
设计意图:
让学生通过实例明确有理数加法的实际意义,明白同一性质的有理数的加法的实际意义。
师生活动:
(1)小王第一次向东走了5m,再向东走了3 m,他向东一共走了多少米?
(2)若都表示有理数,这显然是求两数( )的问题;
(3)怎样求a、b的和呢?
变式练习:
(1)我从教室向餐厅走了20米到旗杆下,再向餐厅走了21米到商店,一共走了多少米?
(二)探索新知,主体探究,导出法则
问题2:既然均是有理数,它们可能是正数,也可能是负数或者零.同学思考一下:的符号可能有几种情况?
设计意图:这种分类让基础差的同学能找到规律,从而解决类似的有理数加法。
师生活动:
根据所学过的数的情况,容易想到有以下几种情况:
(1)同为正数(2)同为负数(3)一个正数一个负数(4)加数中有一个是0;下面我们就来研究这几种情况下有理数的加法问题.在研究之前,首先提醒同学注意正确理解“向东走米”的含义.为了研究的方便起见,用数轴来帮助我们,并设向东为正.
变式练习:
问题3:请你分别把a、b赋予不同情况的有理数,然后进行加法运算,你会有什么样的结论?你能发现有理数的加法法则吗?
设计意图:从特殊到一般让学生更加理解有理数加法的意义
师生活动:
(1)同桌小组合作,主体探究,自主归纳;
(2)学生经过思考,可能会有以下结果(若没有讨论完整教师作适当提示).
情况1:若同为正数:不妨设,用数轴表示如图:(有同学可能会说,这么简单不用数轴也能算出来.这时要告诉它,这里用数轴的目的并不是要结果,而是要体会过程,以便在其他的情况下为用数轴解决问题)显然一共走了35米,写出算式就是:
(+20)+(+15)=+35
情况2:若同为负数:不妨设,这时应怎样用数轴表示?(学生画数轴)这时问题的实际意义是:我向西走了20米后,再向西走了15米,我实际向东走了-35米.即:
情况3:若一正一负:不妨设.请同学们用数轴表示出来,并解说这时问题的实际意义.(如图)(实际意义就是我向东走了20米以后,接着我又向西走了15米.我实际是向东走了5米)即:
情况4:若呢?这时问题的实际意义是什么?怎样用数轴来表示?(同学操作)结果:
情况5:若时,这时问题的实际意义是什么?
结果:
情况6:若时,这时问题的实际意义又是什么?
结果:
情况7:若时,这时问题的实际意义是什么?
结果:
情况8:若时,这时问题的实际意义是什么?
结果:
综合以上几种情况,得到8个式子,我们将这8个式子分成同号、异号、有零的三种情况统计如下:
(1)同号的情况:; .
(2)异号的情况:; ;
; .
(3)有零的情况:; .
同学归纳有理数的加法法则,若归纳不完整,则有其他同学进行补充,直到法则完善化,必要时教师进行点拨:
有理数加法法则
1、同号两数相加,取相同的符号,并把绝对值相加;2、异号两数相加时: (1)若绝对值不相等,取绝对值较大加数的符号,并用较大的绝对值减去较小的绝对值; (2)若绝对值相等,和为0. 也就是相反数的和为0;3、一个数与0的和仍得这个数.
变式练习:
计算:(先口述运用法则的过程,然后说出计算结果)从计算的过程看,你有什么发现?
(1);(2); (3);(4);
(5); (6); (7); (8).
归纳:进行加法运算时首先判断关系、其次确定符号、最后计算绝对值.
三、法则应用、主体反馈
问题4:计算下列各题:
(1) ; (2); (3);
(4); (5).
设计意图:让学生独立完成,在完成的过程中可以让学生进行板演,然后再共同分析过程的正确性,在分析过程的正确性时要充分发挥学生的主体性,让学生充分发表自己的看法,最后得到统一的正确的结论,这样让学生更深刻的理解有理数的加法的意义.
师生活动:
变式练习:
(1) ; (2); (3);
(4); (5).
四、体验探索、发现运算率
问题5: 解决下列问题:
体验1:请你任意取两个有理数(至少有一个是负数),填入下列□和○中,比较它们的运算结果,你能发现什么?
□+○ ○+□
师生活动:
学生独立完成这项任务,自己寻找自己认为合适的有理数,经过运算,可以发现:对任意的两个有理数都有□+○=○+□,即:小学里学的加法交换律在有理数范围内仍成立
体验2:请你任意取三个有理数(至少有一个是负数),填入下列□、○和◇中,比较它们的运算结果,你能发现什么?
(□+○)+◇ □+(○+◇)
师生活动:
学生独立完成这项任务,自己寻找自己认为合适的有理数,经过运算,可以发现:对任意的两个有理数都有(□+○)+◇=□+(○+◇),即:小学里学的加法结合律在有理数范围内仍成立,即:a+b=b+a,(a+b)+c=a+(b+c).
五、应用迁移、巩固提高
问题6: 解决下列问题.
1.计算下列各式.
(1) ;
(2);
(3);
(4)1+(-2)+3+(-4)+……+2005+(-2006).
师生活动:
1、学生独立思考,完成对上述问题的解决,在解决的过程中可能有不同的方法,出现时可以让学生比较各种方法间的异同、优劣,以找到最佳方法,体会运算律的作用.
(1)中运用运算律可以先把正数相加,再把负数相加,然后再把结果相加即可;(2)中运用运算律可以先把第一项和第三项相加、第二项与第四项相加;
(3)运用运算律先把前三项相加、后两项相加;
(4)运用结合律把2006个加数分成1003组,分别相加.
归纳:运算律可以使运算简便(原因是它改变了运算顺序)
2.工地上运来20袋水泥,过秤的结果如下表(单位:千克)
袋号 1 2 3 4 5 6 7 8 9 10
重量 201 204 199 197 203 200 201 202 198 197
袋号 11 12 13 14 15 16 17 18 19 20
重量 196 172 198 203 200 202 201 199 197 205
已知每袋的额定重量为200千克,这批水泥总重量的误差总量是多少千克?
师生活动:
第一步:列出误差表(单位:千克)
袋号 1 2 3 4 5 6 7 8 9 10
误差值 1 4 -1 -3 3 0 1 2 -2 -3
袋号 11 12 13 14 15 16 17 18 19 20
误差值 -4 -28 -2 3 0 2 1 -1 -3 5
注意观察误差值有无互为相反数?所以实际误差总值是袋号7、12、19、20的误差值的和:
=
于是误差总量是不足25千克.
3.一只乌龟沿南北方向的河岸来回爬行,假定向北爬行的路程记为正数,向南爬行的路程记为负数,它爬行的过程记录如下(单位m):-8,7,-3,9,-6,-4,10.
(1) 乌龟最后距离出发点多远,在出发点的南边还是北边;
(2) 求乌龟在整个过程中一共爬行了多远的距离.
师生活动:
学生思考,这个问题可以运用什么知识,由于
(1)求的是乌龟最后距离改为的位置与出发点的距离改为关系,因此可以把上述过程记录加起来,看运算结果即可;
(2)求的是一共爬行的路程,因此把上述过程记录取绝对值后再加起来就行了.
(1)-8+7-3+9-6-4+10=5,所以在出发点的北边;
(2)|-8|+7+|-3|+|9|+|-6|+|-4|+10=47;
所以乌龟在整个过程中一共爬行了47米.
六、课堂小结
1.加法法则(主要是异号两数相加);
2.加法运算律.
七、目标检测:
1、计算:(先口述运用法则的过程,然后说出计算结果)从计算的过程看,你有什么发现?
(1);(2); (3);(4);
(5); (6); (7); (8).
2、计算下列各题:
(1) ; (2); (3);
(4); (5).
八、配餐练习
A组:基础巩固: 习题1、2、3题
B组:强化训练
第1、2题,
(2) ;
(3)
C组:延伸拓广
(1) 第7、8、9、10题;
(2)1+(-2)+3+(-4)+……+2005+(-2006)+2007+(-2008)+2009+(-2010)=___________
o
B
A
20
15
35
PAGE
1
