第四单元第2课时《正比例》精品教学课件 数学北师大版 六年级下册(共17张PPT)
文档属性
| 名称 | 第四单元第2课时《正比例》精品教学课件 数学北师大版 六年级下册(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-29 10:05:33 | ||
图片预览





文档简介
(共17张PPT)
正比例
第四单元 正比例与反比例
输入标题
学习目标
经历比较、分析、归纳等数学活动,提高分析比较、归纳概括能力,初步体会函数思想。
能根据正比例的意义,判断两个相关联的量是不是成正比例,能举出生活中成正比例的实例。
正
比
例
经历正比例意义的建构过程,能从变化中看到“不变”,认识正比例。
输入标题
探究新知
创设情境
巩固新知
课堂小结
布置作业
拓展延伸
上一节课,我们学习了“变化的量”。谁能用自己的话说说什么是“变化的量”?
一个量随着另一个量的变化而发生变化。
这一节课,我们首先来研究正方形的周长、面积随着边长变化会发生什么变化。
复习导入
下面是正方形周长与边长、面积与边长之间的变化情况,把表格填写完整, 并说说你分别发现了什么。
探究新知
巩固新知
课堂小结
布置作业
拓展延伸
创设情境
自主探究
8
12
4
16
4
9
4
16
正方形的面积和周长都是随边长的增加而增加的。
边长/cm 1 2 3
周长/cm 4
边长/cm 1 2 3
面积/cm2 1
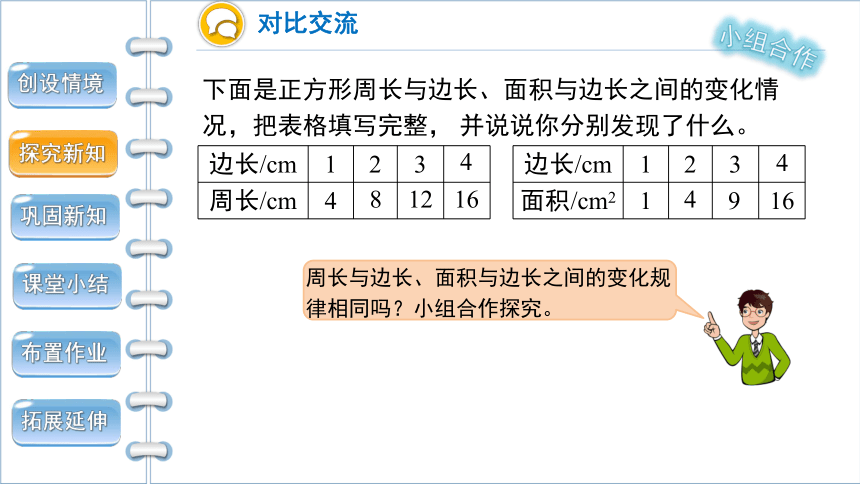
下面是正方形周长与边长、面积与边长之间的变化情况,把表格填写完整, 并说说你分别发现了什么。
探究新知
巩固新知
课堂小结
布置作业
拓展延伸
创设情境
对比交流
周长与边长、面积与边长之间的变化规律相同吗?小组合作探究。
8
12
4
16
4
9
4
16
边长/cm 1 2 3
周长/cm 4
边长/cm 1 2 3
面积/cm2 1
小组合作
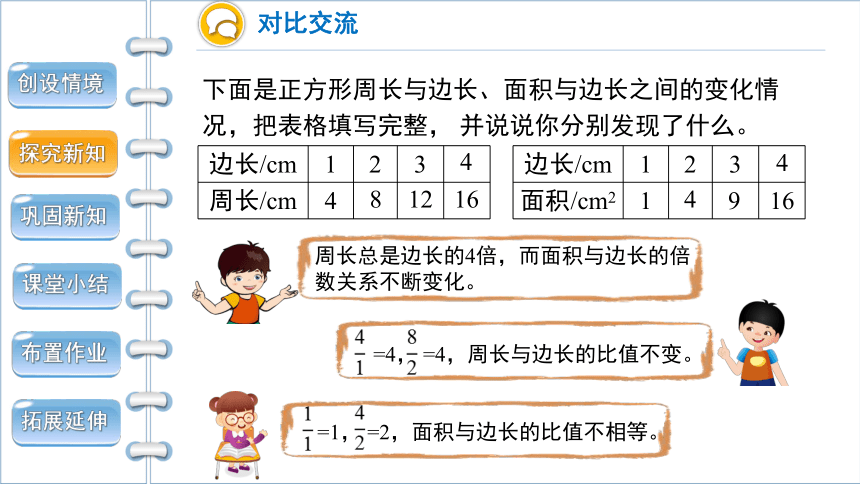
下面是正方形周长与边长、面积与边长之间的变化情况,把表格填写完整, 并说说你分别发现了什么。
探究新知
巩固新知
课堂小结
布置作业
拓展延伸
创设情境
对比交流
周长总是边长的4倍,而面积与边长的倍数关系不断变化。
=4, =4,周长与边长的比值不变。
=1, =2,面积与边长的比值不相等。
8
12
4
16
4
9
4
16
边长/cm 1 2 3
面积/cm2 1
边长/cm 1 2 3
周长/cm 4
一辆汽车以90千米/时的速度行驶,行驶的路程与时间如下。把下表填写完整,你从表中发现了什么
探究新知
巩固新知
课堂小结
布置作业
拓展延伸
创设情境
对比交流
路程随着时间的变化而变化。
时间/时 1 2 3 4 5 6 7
路程/km 90 180 270 360
450
540
630
720
8
90也就是路程与时间的比值是一定的。
一辆汽车以90千米/时的速度行驶,行驶的路程与时间如下。把下表填写完整,你从表中发现了什么
探究新知
巩固新知
课堂小结
布置作业
拓展延伸
创设情境
归纳总结
像这样,路程和时间这两个量,时间变化,所行驶的路程也随着变化,而且路程与时间的比值(速度)一定,我们就说路程和时间成正比例。
时间/时 1 2 3 4 5 6 7
路程/km 90 180 270 360
450
540
630
720
8
下面是正方形周长与边长、面积与边长之间的变化情况,把表格填写完整, 并说说你发现了什么。
探究新知
巩固新知
课堂小结
布置作业
拓展延伸
创设情境
归纳总结
第1个问题中,正方形的周长与边长、面积与边长成正比例吗?
8
12
4
16
4
9
4
16
边长/cm 1 2 3
周长/cm 4
边长/cm 1 2 3
面积/cm2 1
正方形的周长与边长成正比例
正方形的面积与边长不成正比例
一级标题
1. 圆的面积与半径成正比例吗?你是怎么想的?与同伴交流。
巩固新知
探究新知
课堂小结
布置作业
拓展延伸
创设情境
圆的面积公式S = πr2,圆面积随着半径的变化而变化,我想是成正比例的。
我列表试了一试,比值不相等,所以不成正比例。
练习
圆的面积/m 3.14 12.56 28.26
半径/m 1 2 3
比值 3.14 6.28 9.42
一级标题
2.乐乐和爸爸的年龄变化情况如下,把表填写完整。
巩固新知
探究新知
课堂小结
布置作业
拓展延伸
创设情境
他们的年龄成正比例吗?为什么?
他们的年龄不成正比,因为它们的比值在变化。
练习
乐乐的年龄/岁 6 7 8 9 10 11
爸爸的年龄/岁 32 33
35
36
34
37
一级标题
巩固新知
探究新知
课堂小结
布置作业
拓展延伸
创设情境
3.分别举一个成正比例和一个不成正比例的例子,与同伴交流。
单价一定,总价与数量成正比例;人的身高和体重不成正比例。
练习
圆的周长与直径成正比例;
百米赛跑,时间与路程不成正比例。
一级标题
你有什么收获?
如果两个相关联的量,一种量变化另一种量也随着变化,并且这两个量的比值(商)一定,那么就说它们成正比例。
巩固新知
课堂小结
探究新知
布置作业
拓展延伸
创设情境
一级标题
输入标题
教材P42第1题
教材P43第2、3题
课堂小结
布置作业
巩固新知
探究新知
拓展延伸
创设情境
巩固新知
课堂小结
探究新知
布置作业
拓展延伸
创设情境
拓展
据说,埃及的金字塔修成一千多年后,没有人能够准确地测出它的高度。人们尝试过很多方法,但都没有成功。古希腊人泰勒斯用数学方法测量出了金字塔的
高度。泰勒斯站在金字塔前,让
别人测量他影子的长度,当他影
子的长度与他的身高完全相等的
时候,他立刻在金字塔的投影处
作一记号,测量出金字塔影子的
长度。这样,就得到了金字塔的
高度。
巩固新知
课堂小结
探究新知
布置作业
拓展延伸
创设情境
拓展
想一想,说一说,泰勒斯测量金字塔高度的道理是什么 如果身高与影长的比不是1:1时,你还能测量出金字塔的高度吗
如果身高与影长的比不是1:1时,还能测量出金字塔的高度,因为身高与影长的比值等于金字塔的高度与影长的比值。
同一时间,同一地点,物体的高度与影长成正比例。
当身高与影长的比是1 : 1时,金字塔的高度与影长的比也是1 : 1。
再见
正比例
第四单元 正比例与反比例
输入标题
学习目标
经历比较、分析、归纳等数学活动,提高分析比较、归纳概括能力,初步体会函数思想。
能根据正比例的意义,判断两个相关联的量是不是成正比例,能举出生活中成正比例的实例。
正
比
例
经历正比例意义的建构过程,能从变化中看到“不变”,认识正比例。
输入标题
探究新知
创设情境
巩固新知
课堂小结
布置作业
拓展延伸
上一节课,我们学习了“变化的量”。谁能用自己的话说说什么是“变化的量”?
一个量随着另一个量的变化而发生变化。
这一节课,我们首先来研究正方形的周长、面积随着边长变化会发生什么变化。
复习导入
下面是正方形周长与边长、面积与边长之间的变化情况,把表格填写完整, 并说说你分别发现了什么。
探究新知
巩固新知
课堂小结
布置作业
拓展延伸
创设情境
自主探究
8
12
4
16
4
9
4
16
正方形的面积和周长都是随边长的增加而增加的。
边长/cm 1 2 3
周长/cm 4
边长/cm 1 2 3
面积/cm2 1
下面是正方形周长与边长、面积与边长之间的变化情况,把表格填写完整, 并说说你分别发现了什么。
探究新知
巩固新知
课堂小结
布置作业
拓展延伸
创设情境
对比交流
周长与边长、面积与边长之间的变化规律相同吗?小组合作探究。
8
12
4
16
4
9
4
16
边长/cm 1 2 3
周长/cm 4
边长/cm 1 2 3
面积/cm2 1
小组合作
下面是正方形周长与边长、面积与边长之间的变化情况,把表格填写完整, 并说说你分别发现了什么。
探究新知
巩固新知
课堂小结
布置作业
拓展延伸
创设情境
对比交流
周长总是边长的4倍,而面积与边长的倍数关系不断变化。
=4, =4,周长与边长的比值不变。
=1, =2,面积与边长的比值不相等。
8
12
4
16
4
9
4
16
边长/cm 1 2 3
面积/cm2 1
边长/cm 1 2 3
周长/cm 4
一辆汽车以90千米/时的速度行驶,行驶的路程与时间如下。把下表填写完整,你从表中发现了什么
探究新知
巩固新知
课堂小结
布置作业
拓展延伸
创设情境
对比交流
路程随着时间的变化而变化。
时间/时 1 2 3 4 5 6 7
路程/km 90 180 270 360
450
540
630
720
8
90也就是路程与时间的比值是一定的。
一辆汽车以90千米/时的速度行驶,行驶的路程与时间如下。把下表填写完整,你从表中发现了什么
探究新知
巩固新知
课堂小结
布置作业
拓展延伸
创设情境
归纳总结
像这样,路程和时间这两个量,时间变化,所行驶的路程也随着变化,而且路程与时间的比值(速度)一定,我们就说路程和时间成正比例。
时间/时 1 2 3 4 5 6 7
路程/km 90 180 270 360
450
540
630
720
8
下面是正方形周长与边长、面积与边长之间的变化情况,把表格填写完整, 并说说你发现了什么。
探究新知
巩固新知
课堂小结
布置作业
拓展延伸
创设情境
归纳总结
第1个问题中,正方形的周长与边长、面积与边长成正比例吗?
8
12
4
16
4
9
4
16
边长/cm 1 2 3
周长/cm 4
边长/cm 1 2 3
面积/cm2 1
正方形的周长与边长成正比例
正方形的面积与边长不成正比例
一级标题
1. 圆的面积与半径成正比例吗?你是怎么想的?与同伴交流。
巩固新知
探究新知
课堂小结
布置作业
拓展延伸
创设情境
圆的面积公式S = πr2,圆面积随着半径的变化而变化,我想是成正比例的。
我列表试了一试,比值不相等,所以不成正比例。
练习
圆的面积/m 3.14 12.56 28.26
半径/m 1 2 3
比值 3.14 6.28 9.42
一级标题
2.乐乐和爸爸的年龄变化情况如下,把表填写完整。
巩固新知
探究新知
课堂小结
布置作业
拓展延伸
创设情境
他们的年龄成正比例吗?为什么?
他们的年龄不成正比,因为它们的比值在变化。
练习
乐乐的年龄/岁 6 7 8 9 10 11
爸爸的年龄/岁 32 33
35
36
34
37
一级标题
巩固新知
探究新知
课堂小结
布置作业
拓展延伸
创设情境
3.分别举一个成正比例和一个不成正比例的例子,与同伴交流。
单价一定,总价与数量成正比例;人的身高和体重不成正比例。
练习
圆的周长与直径成正比例;
百米赛跑,时间与路程不成正比例。
一级标题
你有什么收获?
如果两个相关联的量,一种量变化另一种量也随着变化,并且这两个量的比值(商)一定,那么就说它们成正比例。
巩固新知
课堂小结
探究新知
布置作业
拓展延伸
创设情境
一级标题
输入标题
教材P42第1题
教材P43第2、3题
课堂小结
布置作业
巩固新知
探究新知
拓展延伸
创设情境
巩固新知
课堂小结
探究新知
布置作业
拓展延伸
创设情境
拓展
据说,埃及的金字塔修成一千多年后,没有人能够准确地测出它的高度。人们尝试过很多方法,但都没有成功。古希腊人泰勒斯用数学方法测量出了金字塔的
高度。泰勒斯站在金字塔前,让
别人测量他影子的长度,当他影
子的长度与他的身高完全相等的
时候,他立刻在金字塔的投影处
作一记号,测量出金字塔影子的
长度。这样,就得到了金字塔的
高度。
巩固新知
课堂小结
探究新知
布置作业
拓展延伸
创设情境
拓展
想一想,说一说,泰勒斯测量金字塔高度的道理是什么 如果身高与影长的比不是1:1时,你还能测量出金字塔的高度吗
如果身高与影长的比不是1:1时,还能测量出金字塔的高度,因为身高与影长的比值等于金字塔的高度与影长的比值。
同一时间,同一地点,物体的高度与影长成正比例。
当身高与影长的比是1 : 1时,金字塔的高度与影长的比也是1 : 1。
再见
