圆柱与圆锥复习课 课件 数学北师大版 六年级下册(共17张PPT)
文档属性
| 名称 | 圆柱与圆锥复习课 课件 数学北师大版 六年级下册(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 129.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-29 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
第一单元 圆柱与圆锥
整理和复习
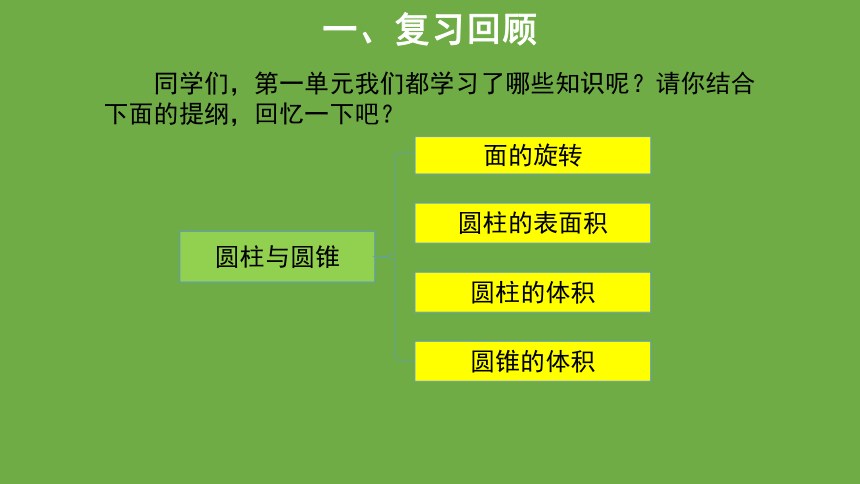
一、复习回顾
同学们,第一单元我们都学习了哪些知识呢?请你结合下面的提纲,回忆一下吧?
圆柱与圆锥
面的旋转
圆柱的体积
圆锥的体积
圆柱的表面积
一、复习回顾
一、面的旋转
圆柱的两个底面是完全相同的两个圆。
两个底面间的距离叫作高。
圆柱有无数条高,且高的长度都相等;
围成圆柱的周围的面是一个曲面,叫作圆柱的侧面。
底面
底面
侧面
O
O'
高
一、复习回顾
一、面的旋转
圆锥的底面是一个圆,圆锥的侧面是一个曲面,从圆锥的顶点到底面圆心的距离是圆锥的高。
圆锥只有一条高。
底面
O
高
侧面
圆柱的表面积=两个底面积+侧面积
二、圆柱的表面积
一、复习回顾
用圆的面积公式S=πr 求出两个底面积。
根据长方形的面积计算方法,会利用公式S侧=πdh或S侧=2πrh求圆柱的侧面积。
一、复习回顾
圆柱的体积计算公式为V=Sh。
三、圆柱的体积
一、复习回顾
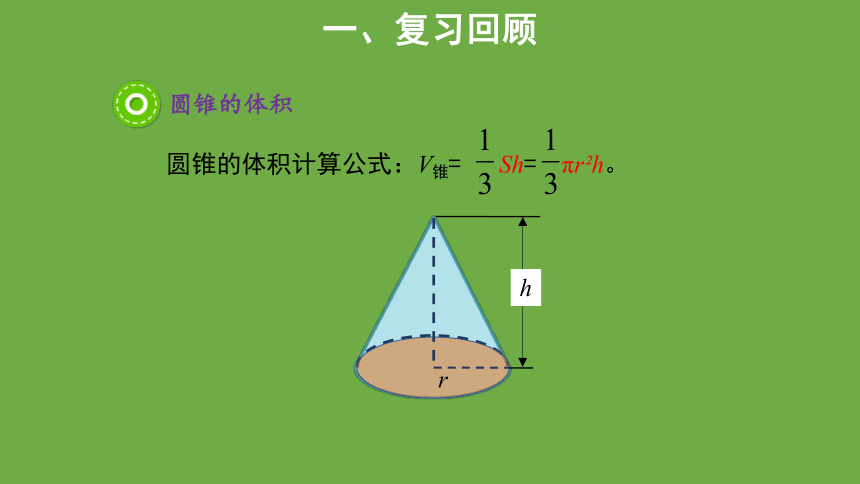
四、圆锥的体积
圆锥的体积计算公式:V锥= Sh= πr h。
r
h
二、基础练习
1. 填空题。
(1)把圆柱的侧面沿高展开,可以得到一个( ),
这个图形的长相当于圆柱的( ),宽相当于圆柱的( )。
(2)一个圆柱的底面半径是3分米,高是2分米,它的侧面积是
( )平方分米,表面积是( )平方分米,体积是( )立方分米。
(3)一个圆柱的底面半径是5厘米,侧面展开图正好是一个正方形,圆柱的高是( )厘米。
长方形
底面周长
高
37.68
94.2
56.52
31.4
二、基础练习
2. 选择题。(把正确答案的序号填在括号里)
(1)求一个圆柱形水桶能盛多少水,就是求这个水桶的( )。
A.侧面积 B.表面积 C.容积 D.体积
(2)圆柱的高不变,底面半径扩大到原来的2倍,它的体积就扩大到原来
( )。
A.4倍 B.8倍 C.16倍 D.12倍
(3)把一个正方体木块加工成一个最大的圆柱,它的底面直径是10厘米,这个正方体木块的体积是( )。
A.8000立方厘米 B.4000立方厘米 C.1000立方厘米 D.314立方厘米
C
A
C
二、基础练习
3. 求出圆柱的表面积和体积。(单位:厘米)
3.14×4×20+3.14×(4÷2) ×2=276.32(平方厘米)
3.14×(4÷2) ×20=251.2(立方厘米)
二、基础练习
4. 一种圆柱形油桶高48厘米,底面直径是20厘米,做这个油桶至少要用铁皮多少平方厘米
3.14×(20÷2)2×2+3.14×20×48=3642.4(平方厘米)
三、易错练习
1. 判断题。(对的画“√”,错的画“ ”)
(1)圆柱的体积都大于圆锥的体积。 ( )
(2)长方体、正方体、圆柱、圆锥的体积都可以用“底面积×高”计算。 ( )
(3)当圆柱的底面周长与高相等时,沿着某一条高剪开,侧面展开图是一个正方形。 ( )
(4)表面积相等的两个圆柱,体积不一定相等。 ( )
×
×
√
√
三、易错练习
2. 一种压路机滚筒的底面周长是1.5米,高是1.2米。如果每分转10周,每分压路多少平方米?
1.5×1.2×10=18(平方米)
四、拓展练习
1. 把一个长5分米、宽3分米、高4分米的长方体铁块熔铸成底面积为6平方分米的圆柱。圆柱的高是多少分米
5×3×4÷6=10(分米)
四、拓展练习
2. 把一根长1.2米的圆柱形钢材截成3段小圆柱,表面积增加了6.28平方分米。原来这根钢材的体积是多少
(3-1)×2=4(面)
1.2米=12分米
6.28÷4×12=18.84(立方分米)
四、拓展练习
3. 等底等高的圆柱和圆锥体积之和是12.56立方厘米,圆柱的体积是多少?
圆柱体积:12.56÷4×3=9.42(m3)
再见
第一单元 圆柱与圆锥
整理和复习
一、复习回顾
同学们,第一单元我们都学习了哪些知识呢?请你结合下面的提纲,回忆一下吧?
圆柱与圆锥
面的旋转
圆柱的体积
圆锥的体积
圆柱的表面积
一、复习回顾
一、面的旋转
圆柱的两个底面是完全相同的两个圆。
两个底面间的距离叫作高。
圆柱有无数条高,且高的长度都相等;
围成圆柱的周围的面是一个曲面,叫作圆柱的侧面。
底面
底面
侧面
O
O'
高
一、复习回顾
一、面的旋转
圆锥的底面是一个圆,圆锥的侧面是一个曲面,从圆锥的顶点到底面圆心的距离是圆锥的高。
圆锥只有一条高。
底面
O
高
侧面
圆柱的表面积=两个底面积+侧面积
二、圆柱的表面积
一、复习回顾
用圆的面积公式S=πr 求出两个底面积。
根据长方形的面积计算方法,会利用公式S侧=πdh或S侧=2πrh求圆柱的侧面积。
一、复习回顾
圆柱的体积计算公式为V=Sh。
三、圆柱的体积
一、复习回顾
四、圆锥的体积
圆锥的体积计算公式:V锥= Sh= πr h。
r
h
二、基础练习
1. 填空题。
(1)把圆柱的侧面沿高展开,可以得到一个( ),
这个图形的长相当于圆柱的( ),宽相当于圆柱的( )。
(2)一个圆柱的底面半径是3分米,高是2分米,它的侧面积是
( )平方分米,表面积是( )平方分米,体积是( )立方分米。
(3)一个圆柱的底面半径是5厘米,侧面展开图正好是一个正方形,圆柱的高是( )厘米。
长方形
底面周长
高
37.68
94.2
56.52
31.4
二、基础练习
2. 选择题。(把正确答案的序号填在括号里)
(1)求一个圆柱形水桶能盛多少水,就是求这个水桶的( )。
A.侧面积 B.表面积 C.容积 D.体积
(2)圆柱的高不变,底面半径扩大到原来的2倍,它的体积就扩大到原来
( )。
A.4倍 B.8倍 C.16倍 D.12倍
(3)把一个正方体木块加工成一个最大的圆柱,它的底面直径是10厘米,这个正方体木块的体积是( )。
A.8000立方厘米 B.4000立方厘米 C.1000立方厘米 D.314立方厘米
C
A
C
二、基础练习
3. 求出圆柱的表面积和体积。(单位:厘米)
3.14×4×20+3.14×(4÷2) ×2=276.32(平方厘米)
3.14×(4÷2) ×20=251.2(立方厘米)
二、基础练习
4. 一种圆柱形油桶高48厘米,底面直径是20厘米,做这个油桶至少要用铁皮多少平方厘米
3.14×(20÷2)2×2+3.14×20×48=3642.4(平方厘米)
三、易错练习
1. 判断题。(对的画“√”,错的画“ ”)
(1)圆柱的体积都大于圆锥的体积。 ( )
(2)长方体、正方体、圆柱、圆锥的体积都可以用“底面积×高”计算。 ( )
(3)当圆柱的底面周长与高相等时,沿着某一条高剪开,侧面展开图是一个正方形。 ( )
(4)表面积相等的两个圆柱,体积不一定相等。 ( )
×
×
√
√
三、易错练习
2. 一种压路机滚筒的底面周长是1.5米,高是1.2米。如果每分转10周,每分压路多少平方米?
1.5×1.2×10=18(平方米)
四、拓展练习
1. 把一个长5分米、宽3分米、高4分米的长方体铁块熔铸成底面积为6平方分米的圆柱。圆柱的高是多少分米
5×3×4÷6=10(分米)
四、拓展练习
2. 把一根长1.2米的圆柱形钢材截成3段小圆柱,表面积增加了6.28平方分米。原来这根钢材的体积是多少
(3-1)×2=4(面)
1.2米=12分米
6.28÷4×12=18.84(立方分米)
四、拓展练习
3. 等底等高的圆柱和圆锥体积之和是12.56立方厘米,圆柱的体积是多少?
圆柱体积:12.56÷4×3=9.42(m3)
再见
