总复习式与方程、正比例与反比例、常见的量示范教学课件(共22张ppt) 数学北师大版 六年级下册
文档属性
| 名称 | 总复习式与方程、正比例与反比例、常见的量示范教学课件(共22张ppt) 数学北师大版 六年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 266.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-29 13:49:10 | ||
图片预览








文档简介
(共22张PPT)
总复习
式与方程
正比例与反比例
常见的量
一、复习回顾
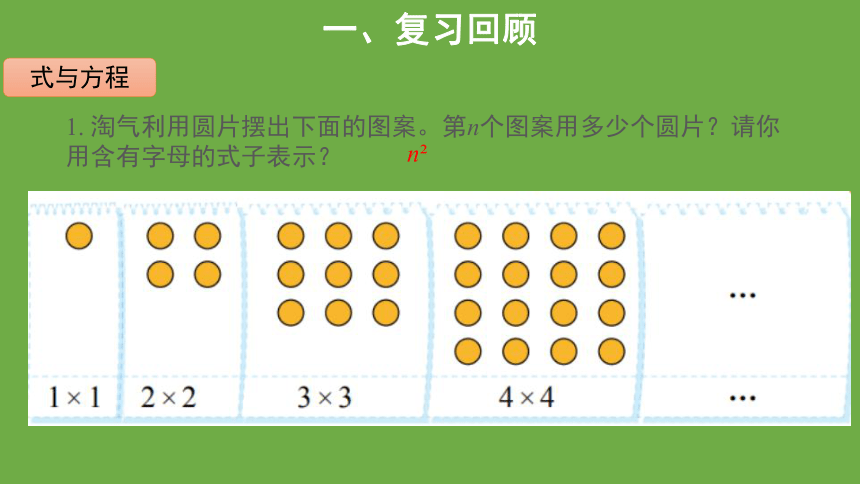
1. 淘气利用圆片摆出下面的图案。第n个图案用多少个圆片?请你用含有字母的式子表示?
式与方程
n
一、复习回顾
2. 我们已经学过一些公式和规律,请你用含有字母的式子把它们表示出来。
运算定律 用字母表示
加法交换律 a+b=b+a
加法结合律
乘法交换律
乘法结合律
乘法分配律
(a+b)+c=a+(b+c)
a b=b a或ab=ba
(a b) c=a (b c) 或(ab) c=a (bc)
(a+b) c=a c+b c或(a+b)c=ac+bc
式与方程
一、复习回顾
3. 在解方程时可以利用等式的性质,你还记得等式的性质是什么吗?在解方程中又要注意一些什么呢?
等式两边都加上(或减去)同一个数,等式仍然成立。
等式两边都乘同一个数(或除以同一个不为0的数),等式成立。
解方程记得写“解”;解的过程中各等号要对齐;解的结果记得检验 。
式与方程
一、复习回顾
4. 我们一起学习了列方程解决问题,你还记得最重要的是什么吗?
式与方程
找等量关系
一、复习回顾
1. 什么是比?什么是比例?它们又有什么应用呢?
两个数相除又叫两个数的比。
表示两个比相等的式子叫作比例。
可以根据比的基本性质(比的前项和后项都乘或除以同一个数(0除外),比值不变)化简比。
“在比例里两个内项的乘积等于两个外项的乘积”,可以根据这个性质解比例。
正比例与反比例
一、复习回顾
2. 你知道比、分数、除法之间的关系吗?
比的前项相当于分子,比的后项相当于分母,比号相当于分数线。
比的前项相当于被除数,比的后项相当于除数,比号相当于除号。
正比例与反比例
一、复习回顾
1. 读一读,你能说一说哪些是质量单位,哪些是长度单位吗?
常见的量
李雪英在 2012 年伦敦奥运会女子举重 58 kg 级决赛中,以 246 kg 的总成绩夺得冠军,并打破抓举和总成绩的奥运会纪录。
孙杨在 2012 年伦敦奥运会男子 1500 m 自由泳决赛中,以 14 分 31 秒 02 的成绩夺得冠军,并打破了世界纪录。
一、复习回顾
2. 你知道常见的量有哪些吗?
质量单位:千克、克、吨。
时间单位:时、分、秒和年、月、日等。
人民币单位:元、角、分。
常见的量
二、基础练习
1. 填一填。
(1)比 x 少 25 的数是 ( )。
(2)n 的 5 倍与 m 的差是 ( )。
(3)一件衬衫 a 元,一件毛衣的价格比它的 2 倍还多 6 元,毛衣的价格是( ) 元。
(4)原价 a 元的产品打八折后的价钱是( )元。
x-25
5n-m
2a+6
0.8a
二、基础练习
2. 下图中,圆的半径是r,请你用含有字母的式子表示出正方形的周长和面积。
C=8r
S=4r
二、基础练习
3. 解方程。
6x-35=13 (100-3x)÷2=8
解:6x-35+35=13+35
6x=48
6x÷6=48÷6
x=8
解:(100-3x) ÷2×2=8×2
100-3x=16
100-3x+3x=16+3x
100=16+3x
16+3x=100
16+3x-16=100-16
3x=84
3x÷3=84÷3
x=28
二、基础练习
4. 填一填。
(1)两个正方形的边长比是 1∶3 ,周长比是( ),面积比是( )。
(2)9元可以买2 kg 鸡蛋,总价与数量的比是( ),比值是( )。
(3)汽车3小时行150 km,路程与时间的比是( ),比值是( )。
1∶3
1∶9
9∶2
4.5
50∶1
50
二、基础练习
5. 单位换算。
1.7 吨 =( )千克 3.5 日 =( )日( )时
2.5 分 =( )秒 1.2 小时 =( )小时( )分
3 吨 40 千克 =( )吨 40 元 =( )分
1700
3
12
150
1
12
3.04
4000
三、易错练习
1. 两车分别从 A,B 两地同时出发,相向而行,经过2.5小时相遇。 (1)两地间的距离是多少?
(2)当a= 45,b= 60 时,求两地间的距离。
(1)2.5(a+b)
(2)2.5×(45+60)=262.5(千米)
三、易错练习
2. 判断下面每题中的两个量是否成正比例或反比例。
(1)一捆100 m长的电线,用去的长度与剩下的长度。
(2)三角形的面积一定,它的底和高。
(3)一个数与它的倒数。
(1)不成比例
(2)成反比例
(3)成反比例
三、易错练习
3. 育才小学六年级同学从学校出发,乘车0.5小时,来到离学校5 km远的科技馆,参观1小时,出馆后休息0.5小时,然后乘车0.5小时返回学校。下面三幅图中, 哪幅描述了他们的这一活动行程呢?选一选。
√
三、易错练习
4. 找规律,填一填。
(1)8,11,14,17,( ),23,( );
(2)4,9,16,25,( ),49,64;
(3)1,8,27,( ),125,( );
(4),,,,,
20
26
36
64
216
3
6
5
10
6
12
四、拓展练习
1.甲、乙两个工程队同修一条公路,它们从两端同时施工。
(1)甲队每天修a m,乙队每天修 b m,8天修完。这条公路长多少米?
(2)如果这条公路长 3000 m,甲队每天修85 m,乙队每天修65 m,修完这条公路需要几天?
(1)8(a+b)
(2)解:设修完这条公路需要x天。
(85+65)x=3000
150x=3000
x=3000÷150
x=20
四、拓展练习
2. 小芳和小兰共储蓄 505 元,小兰储蓄的钱数比小芳的 3 倍少 15 元,小兰储蓄多少钱?
解:设小芳储蓄的钱数为x元。
x+(3x-15)=505
4x-15=505
4x=520
x=130
3x-15=3×130-15=375
答:小兰储蓄 375 元。
四、拓展练习
3. 聪聪今年 8 岁,爸爸今年 34 岁,聪聪多少岁时,爸爸的年龄是聪聪的 3 倍?
解:设聪聪x岁时,爸爸的年龄是聪聪的 3 倍。
3x-x=34-8
2x=26
2x÷2=26÷2
x=13
答:聪聪 13 岁时,爸爸的年龄是聪聪的 3 倍。
再见
总复习
式与方程
正比例与反比例
常见的量
一、复习回顾
1. 淘气利用圆片摆出下面的图案。第n个图案用多少个圆片?请你用含有字母的式子表示?
式与方程
n
一、复习回顾
2. 我们已经学过一些公式和规律,请你用含有字母的式子把它们表示出来。
运算定律 用字母表示
加法交换律 a+b=b+a
加法结合律
乘法交换律
乘法结合律
乘法分配律
(a+b)+c=a+(b+c)
a b=b a或ab=ba
(a b) c=a (b c) 或(ab) c=a (bc)
(a+b) c=a c+b c或(a+b)c=ac+bc
式与方程
一、复习回顾
3. 在解方程时可以利用等式的性质,你还记得等式的性质是什么吗?在解方程中又要注意一些什么呢?
等式两边都加上(或减去)同一个数,等式仍然成立。
等式两边都乘同一个数(或除以同一个不为0的数),等式成立。
解方程记得写“解”;解的过程中各等号要对齐;解的结果记得检验 。
式与方程
一、复习回顾
4. 我们一起学习了列方程解决问题,你还记得最重要的是什么吗?
式与方程
找等量关系
一、复习回顾
1. 什么是比?什么是比例?它们又有什么应用呢?
两个数相除又叫两个数的比。
表示两个比相等的式子叫作比例。
可以根据比的基本性质(比的前项和后项都乘或除以同一个数(0除外),比值不变)化简比。
“在比例里两个内项的乘积等于两个外项的乘积”,可以根据这个性质解比例。
正比例与反比例
一、复习回顾
2. 你知道比、分数、除法之间的关系吗?
比的前项相当于分子,比的后项相当于分母,比号相当于分数线。
比的前项相当于被除数,比的后项相当于除数,比号相当于除号。
正比例与反比例
一、复习回顾
1. 读一读,你能说一说哪些是质量单位,哪些是长度单位吗?
常见的量
李雪英在 2012 年伦敦奥运会女子举重 58 kg 级决赛中,以 246 kg 的总成绩夺得冠军,并打破抓举和总成绩的奥运会纪录。
孙杨在 2012 年伦敦奥运会男子 1500 m 自由泳决赛中,以 14 分 31 秒 02 的成绩夺得冠军,并打破了世界纪录。
一、复习回顾
2. 你知道常见的量有哪些吗?
质量单位:千克、克、吨。
时间单位:时、分、秒和年、月、日等。
人民币单位:元、角、分。
常见的量
二、基础练习
1. 填一填。
(1)比 x 少 25 的数是 ( )。
(2)n 的 5 倍与 m 的差是 ( )。
(3)一件衬衫 a 元,一件毛衣的价格比它的 2 倍还多 6 元,毛衣的价格是( ) 元。
(4)原价 a 元的产品打八折后的价钱是( )元。
x-25
5n-m
2a+6
0.8a
二、基础练习
2. 下图中,圆的半径是r,请你用含有字母的式子表示出正方形的周长和面积。
C=8r
S=4r
二、基础练习
3. 解方程。
6x-35=13 (100-3x)÷2=8
解:6x-35+35=13+35
6x=48
6x÷6=48÷6
x=8
解:(100-3x) ÷2×2=8×2
100-3x=16
100-3x+3x=16+3x
100=16+3x
16+3x=100
16+3x-16=100-16
3x=84
3x÷3=84÷3
x=28
二、基础练习
4. 填一填。
(1)两个正方形的边长比是 1∶3 ,周长比是( ),面积比是( )。
(2)9元可以买2 kg 鸡蛋,总价与数量的比是( ),比值是( )。
(3)汽车3小时行150 km,路程与时间的比是( ),比值是( )。
1∶3
1∶9
9∶2
4.5
50∶1
50
二、基础练习
5. 单位换算。
1.7 吨 =( )千克 3.5 日 =( )日( )时
2.5 分 =( )秒 1.2 小时 =( )小时( )分
3 吨 40 千克 =( )吨 40 元 =( )分
1700
3
12
150
1
12
3.04
4000
三、易错练习
1. 两车分别从 A,B 两地同时出发,相向而行,经过2.5小时相遇。 (1)两地间的距离是多少?
(2)当a= 45,b= 60 时,求两地间的距离。
(1)2.5(a+b)
(2)2.5×(45+60)=262.5(千米)
三、易错练习
2. 判断下面每题中的两个量是否成正比例或反比例。
(1)一捆100 m长的电线,用去的长度与剩下的长度。
(2)三角形的面积一定,它的底和高。
(3)一个数与它的倒数。
(1)不成比例
(2)成反比例
(3)成反比例
三、易错练习
3. 育才小学六年级同学从学校出发,乘车0.5小时,来到离学校5 km远的科技馆,参观1小时,出馆后休息0.5小时,然后乘车0.5小时返回学校。下面三幅图中, 哪幅描述了他们的这一活动行程呢?选一选。
√
三、易错练习
4. 找规律,填一填。
(1)8,11,14,17,( ),23,( );
(2)4,9,16,25,( ),49,64;
(3)1,8,27,( ),125,( );
(4),,,,,
20
26
36
64
216
3
6
5
10
6
12
四、拓展练习
1.甲、乙两个工程队同修一条公路,它们从两端同时施工。
(1)甲队每天修a m,乙队每天修 b m,8天修完。这条公路长多少米?
(2)如果这条公路长 3000 m,甲队每天修85 m,乙队每天修65 m,修完这条公路需要几天?
(1)8(a+b)
(2)解:设修完这条公路需要x天。
(85+65)x=3000
150x=3000
x=3000÷150
x=20
四、拓展练习
2. 小芳和小兰共储蓄 505 元,小兰储蓄的钱数比小芳的 3 倍少 15 元,小兰储蓄多少钱?
解:设小芳储蓄的钱数为x元。
x+(3x-15)=505
4x-15=505
4x=520
x=130
3x-15=3×130-15=375
答:小兰储蓄 375 元。
四、拓展练习
3. 聪聪今年 8 岁,爸爸今年 34 岁,聪聪多少岁时,爸爸的年龄是聪聪的 3 倍?
解:设聪聪x岁时,爸爸的年龄是聪聪的 3 倍。
3x-x=34-8
2x=26
2x÷2=26÷2
x=13
答:聪聪 13 岁时,爸爸的年龄是聪聪的 3 倍。
再见
