总复习图形与几何 示范课件(共26张ppt) 数学北师大版 六年级下册
文档属性
| 名称 | 总复习图形与几何 示范课件(共26张ppt) 数学北师大版 六年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 417.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-29 00:00:00 | ||
图片预览





文档简介
(共26张PPT)
总复习
图形与几何
一、复习回顾
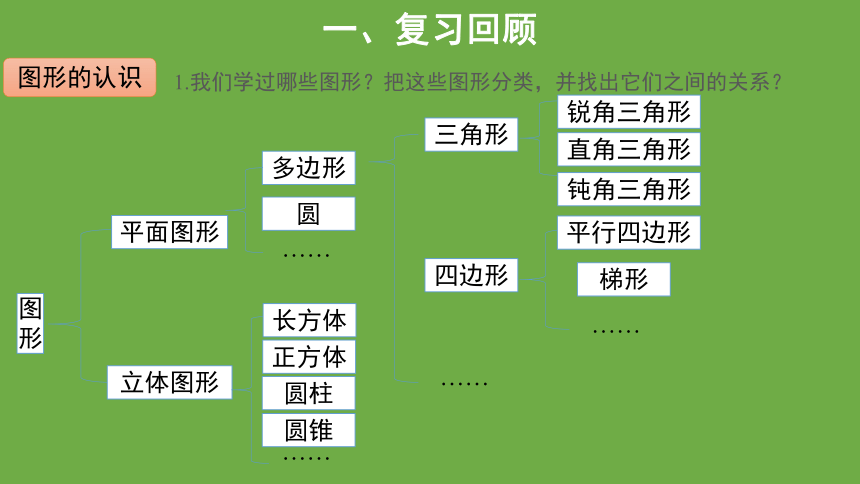
1.我们学过哪些图形?把这些图形分类,并找出它们之间的关系?
图形的认识
图形
多边形
圆
立体图形
平面图形
三角形
锐角三角形
直角三角形
钝角三角形
四边形
平行四边形
梯形
……
……
长方体
正方体
圆柱
圆锥
……
……
一、复习回顾
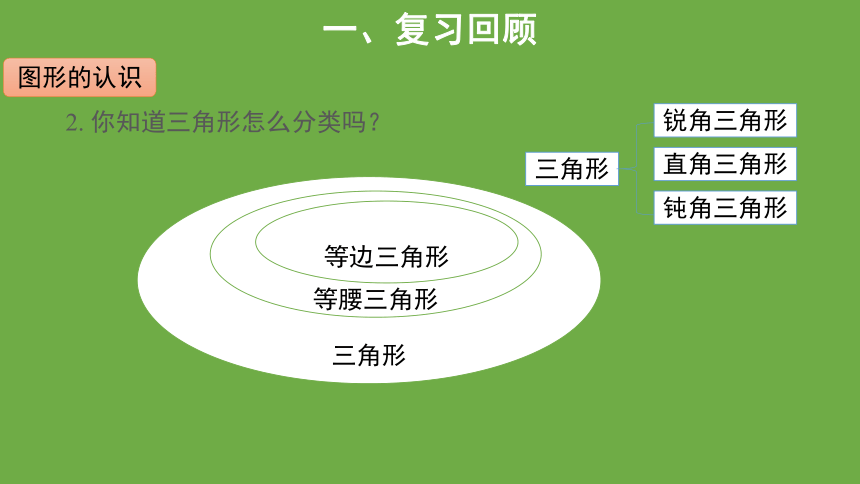
2. 你知道三角形怎么分类吗?
图形的认识
三角形
等腰三角形
等边三角形
三角形
锐角三角形
直角三角形
钝角三角形
一、复习回顾
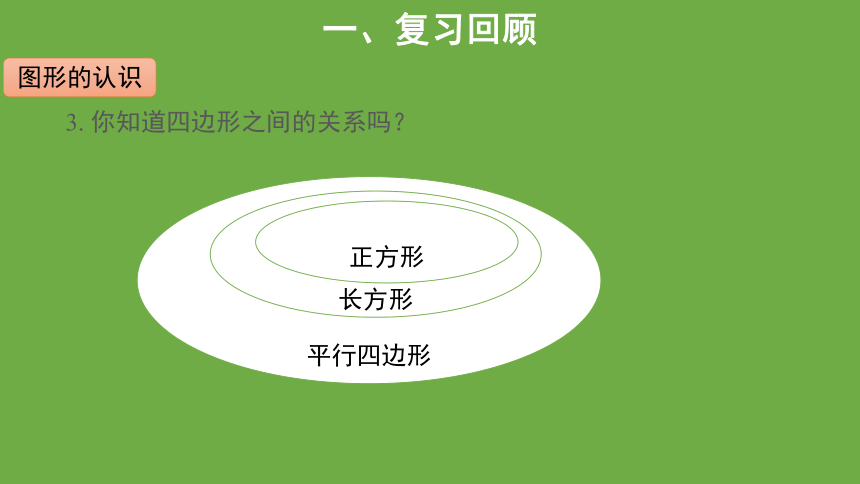
3. 你知道四边形之间的关系吗?
图形的认识
平行四边形
长方形
正方形
一、复习回顾
4. 你知道角有哪些吗?它们的范围又是多少呢?
图形的认识
锐角
小于90°
直角
等于90°
钝角
大于90°
平角
等于180°
周角
等于360°
一、复习回顾
1. 说一说你对长度、面积、体积的认识。
长度是线段的长短。
面积是面的大小。
体积是物体所占空间的大小。
图形与测量
一、复习回顾
2. 测量需要单位,你知道常用的长度、面积、体积单位分别有哪些吗?进率分别是多少呢?
图形与测量
10
10
10
100
100
100
1000
1000
1000
1000
一、复习回顾
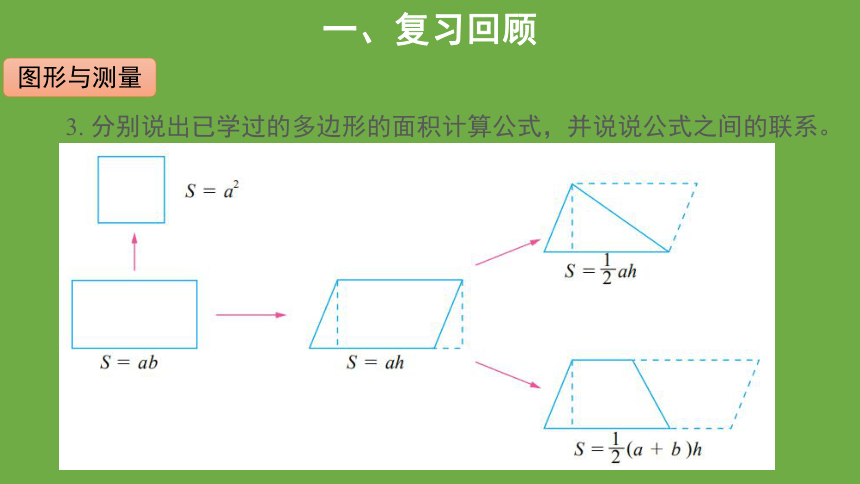
3. 分别说出已学过的多边形的面积计算公式,并说说公式之间的联系。
图形与测量
一、复习回顾
4. 你知道圆的面积计算公式是什么吗?
S=πr
图形与测量
一、复习回顾
5. 分别说出已学过的立体图形的体积计算公式,并说说公式之间的联系。
图形与测量
一、复习回顾
1. 我们一起认识过图形的那些运动现象呢?
平移、旋转、轴对称。
2. 在学过的图形中,哪些图形是轴对称图形?它们分别有多少条对称轴?
长方形有2条对称轴;正方形有4条对称轴;圆有无数条对称轴。
图形的运动
一、复习回顾
1. 你还记得确定位置的两种基本方法是什么吗?
利用数对表示位置。
根据方向和距离确定物体的位置。
图形与位置
二、基础练习
1. 求下面三角形中各角的度数。
∠1 =( ) ∠ 2 = ( ) ∠ 3 =( )
60°
60°
60°
二、基础练习
2. 上面一排图形旋转后会得到下面的哪个图形?想一想,连一连。
二、基础练习
3. 填一填。
0.4 m =( )cm 725 mm =( )dm
3.2 m =( )dm 5 dm =( )cm
7500 mL =( )L 6.2 dm =( )m
40
7.25
320
500
7.5
0.062
二、基础练习
4. 下列图案中,哪些不是轴对称图形?
不是
不是
三、易错练习
1. 在能围成三角形的一组线段下面画“√”。(单位:cm)
√
三、易错练习
2. 填一填。
下图是由5个棱长为 1 cm 的正方体搭成的,将这个立体图形的表面涂上红色。其中只有三面涂上红色的正方体有( )个,只有四面涂上红色的正方体有( )个,五面涂上红色的正方体有( )个。
1
3
1
三、易错练习
3. 填上合适的单位。
(1)水杯高约1( )。
(2)跳绳长约2( )。
(3)淘气腰围约60( )。
(4)一枚邮票的面积是4( )。
(5)一个人一次能喝约500( ) 的水 。
(6)牙膏盒的体积约是40( )。
dm
m
cm
cm
mL
cm
三、易错练习
4. 图形A,B,C的面积分别是多少平方厘米?图形D的面积大约是多少平方厘 米?(每格面积为 1 cm )
A: ( )
B: ( )
C: ( )
D:( )
5 cm
6 cm
2 cm
9 cm
三、易错练习
5. 看图填空。
123 路汽车从飞机场到明慧园的行驶路线是:向( )行驶( )站到商场, 再向( )行驶( )站到体育馆,再向( )行驶( )站到明慧园。
北
2
东
3
东北
1
四、拓展练习
1. 求下面各图形中涂色部分的面积。
(1)(60+80)×30÷2-60×20÷2=1500(dm )
(2)7×4+(15-4)×(7-4)=61(dm )
四、拓展练习
2. 如图,圆的周长是62.8 cm。正方形的周长是多少?
62.8÷3.14=20(cm)
20×4=80(cm)
四、拓展练习
3. 用一根长 48 dm 的铁丝做一个长方体的框架,使它的高为 8 dm,长、宽的比是1∶1。再把它的五个面糊上纸,做成一个长方体的灯笼,至少需要多少平方分米的纸?
48÷4=12(dm)
12-8=4(dm)
4× =2(dm)
表面积:2×8×4+2×2=68(dm )
四、拓展练习
4. 如图,笑笑家在经 2 路与纬 2 路的交叉路口,如果用(2,2)→(2,3)→(2,4) →(3,4)→(4,4)表示笑笑从家到健身中心的一条路线,那么,你能用同样的方法表示笑笑从家到健身中心的另一条路线吗?
答案不唯一。
(2,2)→(3,2)→
(4,2)→(4,3)→
(4,4)
再见
总复习
图形与几何
一、复习回顾
1.我们学过哪些图形?把这些图形分类,并找出它们之间的关系?
图形的认识
图形
多边形
圆
立体图形
平面图形
三角形
锐角三角形
直角三角形
钝角三角形
四边形
平行四边形
梯形
……
……
长方体
正方体
圆柱
圆锥
……
……
一、复习回顾
2. 你知道三角形怎么分类吗?
图形的认识
三角形
等腰三角形
等边三角形
三角形
锐角三角形
直角三角形
钝角三角形
一、复习回顾
3. 你知道四边形之间的关系吗?
图形的认识
平行四边形
长方形
正方形
一、复习回顾
4. 你知道角有哪些吗?它们的范围又是多少呢?
图形的认识
锐角
小于90°
直角
等于90°
钝角
大于90°
平角
等于180°
周角
等于360°
一、复习回顾
1. 说一说你对长度、面积、体积的认识。
长度是线段的长短。
面积是面的大小。
体积是物体所占空间的大小。
图形与测量
一、复习回顾
2. 测量需要单位,你知道常用的长度、面积、体积单位分别有哪些吗?进率分别是多少呢?
图形与测量
10
10
10
100
100
100
1000
1000
1000
1000
一、复习回顾
3. 分别说出已学过的多边形的面积计算公式,并说说公式之间的联系。
图形与测量
一、复习回顾
4. 你知道圆的面积计算公式是什么吗?
S=πr
图形与测量
一、复习回顾
5. 分别说出已学过的立体图形的体积计算公式,并说说公式之间的联系。
图形与测量
一、复习回顾
1. 我们一起认识过图形的那些运动现象呢?
平移、旋转、轴对称。
2. 在学过的图形中,哪些图形是轴对称图形?它们分别有多少条对称轴?
长方形有2条对称轴;正方形有4条对称轴;圆有无数条对称轴。
图形的运动
一、复习回顾
1. 你还记得确定位置的两种基本方法是什么吗?
利用数对表示位置。
根据方向和距离确定物体的位置。
图形与位置
二、基础练习
1. 求下面三角形中各角的度数。
∠1 =( ) ∠ 2 = ( ) ∠ 3 =( )
60°
60°
60°
二、基础练习
2. 上面一排图形旋转后会得到下面的哪个图形?想一想,连一连。
二、基础练习
3. 填一填。
0.4 m =( )cm 725 mm =( )dm
3.2 m =( )dm 5 dm =( )cm
7500 mL =( )L 6.2 dm =( )m
40
7.25
320
500
7.5
0.062
二、基础练习
4. 下列图案中,哪些不是轴对称图形?
不是
不是
三、易错练习
1. 在能围成三角形的一组线段下面画“√”。(单位:cm)
√
三、易错练习
2. 填一填。
下图是由5个棱长为 1 cm 的正方体搭成的,将这个立体图形的表面涂上红色。其中只有三面涂上红色的正方体有( )个,只有四面涂上红色的正方体有( )个,五面涂上红色的正方体有( )个。
1
3
1
三、易错练习
3. 填上合适的单位。
(1)水杯高约1( )。
(2)跳绳长约2( )。
(3)淘气腰围约60( )。
(4)一枚邮票的面积是4( )。
(5)一个人一次能喝约500( ) 的水 。
(6)牙膏盒的体积约是40( )。
dm
m
cm
cm
mL
cm
三、易错练习
4. 图形A,B,C的面积分别是多少平方厘米?图形D的面积大约是多少平方厘 米?(每格面积为 1 cm )
A: ( )
B: ( )
C: ( )
D:( )
5 cm
6 cm
2 cm
9 cm
三、易错练习
5. 看图填空。
123 路汽车从飞机场到明慧园的行驶路线是:向( )行驶( )站到商场, 再向( )行驶( )站到体育馆,再向( )行驶( )站到明慧园。
北
2
东
3
东北
1
四、拓展练习
1. 求下面各图形中涂色部分的面积。
(1)(60+80)×30÷2-60×20÷2=1500(dm )
(2)7×4+(15-4)×(7-4)=61(dm )
四、拓展练习
2. 如图,圆的周长是62.8 cm。正方形的周长是多少?
62.8÷3.14=20(cm)
20×4=80(cm)
四、拓展练习
3. 用一根长 48 dm 的铁丝做一个长方体的框架,使它的高为 8 dm,长、宽的比是1∶1。再把它的五个面糊上纸,做成一个长方体的灯笼,至少需要多少平方分米的纸?
48÷4=12(dm)
12-8=4(dm)
4× =2(dm)
表面积:2×8×4+2×2=68(dm )
四、拓展练习
4. 如图,笑笑家在经 2 路与纬 2 路的交叉路口,如果用(2,2)→(2,3)→(2,4) →(3,4)→(4,4)表示笑笑从家到健身中心的一条路线,那么,你能用同样的方法表示笑笑从家到健身中心的另一条路线吗?
答案不唯一。
(2,2)→(3,2)→
(4,2)→(4,3)→
(4,4)
再见
