北师大版数学六年级下册 总复习-数的认识 第二课时 小数、分数、百分数课件(共22张PPT)
文档属性
| 名称 | 北师大版数学六年级下册 总复习-数的认识 第二课时 小数、分数、百分数课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-29 14:11:07 | ||
图片预览







文档简介
(共22张PPT)
总 复 习
数的认识
第二课时 小数、分数、百分数
目 录
情景导学
1
探索与发现
2
学以致用
3
课后作业
4
情景导学
01
情景导学
用尽可能多的方式解释“ ”的含义。
把3个苹果平均分成4份,求每份有多少个苹果,用除法计算:3÷4= (个),每份是 个苹果。这里的 表示具体的数量。
探索与发现
02
探索与发现
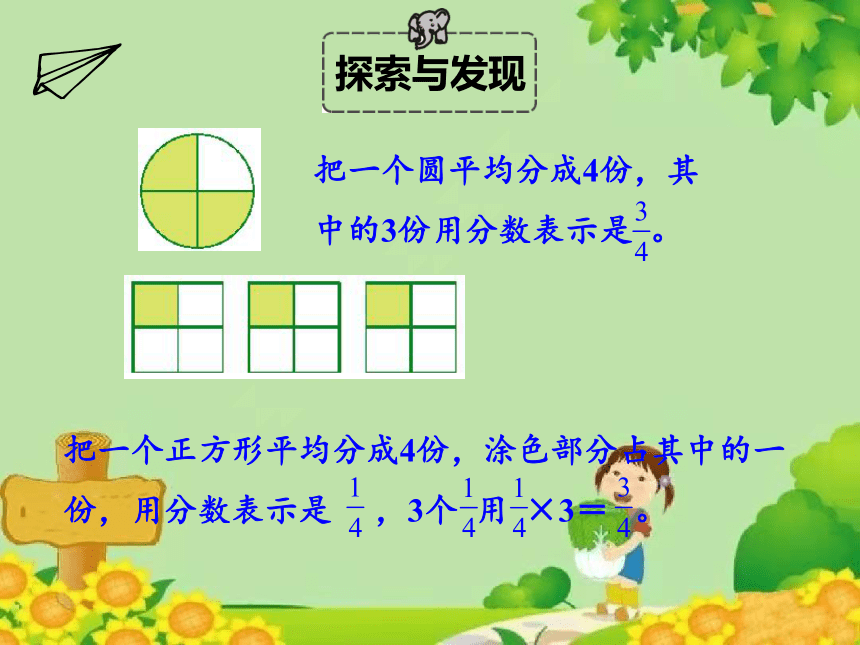
把一个圆平均分成4份,其中的3份用分数表示是 。
把一个正方形平均分成4份,涂色部分占其中的一份,用分数表示是 ,3个 用 ×3= 。
探索与发现
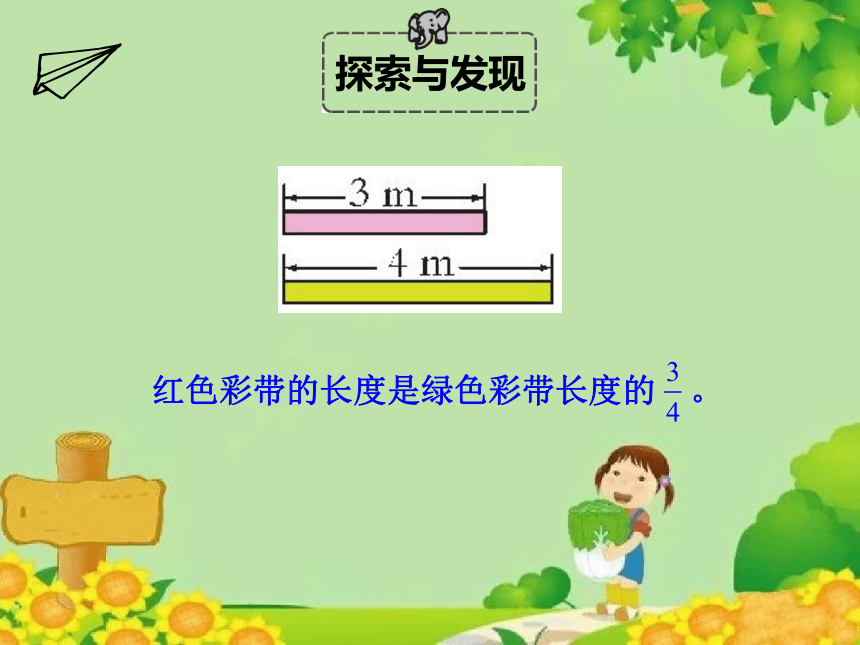
红色彩带的长度是绿色彩带长度的 。
探索与发现
结合具体的例子说一说。
(1)小数、分数、百分数之间的关系。
(2)分数、除法之间的关系。
(3)商不变的规律与分数基本性质的关系。
探索与发现
(1)小数、分数、百分数之间的关系。
小数的意义:小数实际是十进制分数的另一种形式,十分之一、百分之一、千分之一……的分数都可以用小数表示,如:0.1、0.01、0.001……。
探索与发现
分数的意义:把单位“1”平均分成若干份,表示这样的一份或几份的数叫作分数。
分数可以表示两种含义:后面带计量单位可以表示一个具体的量,
如:一个菠萝重3/4 kg、一根绳子长1/4m;不带计量单位可以表示两个量的倍数关系,如:小明身高是小红身高的4/5。
探索与发现
百分数的意义:表示一个数是另一个数的百分之几的数叫作百分数。
百分数只能表示一个量是另一个量的百分之几,不能带上计量单位来表示具体的量。
如:六年级参加兴趣活动的同学占全年级人数的80%。
探索与发现
小数、分数、百分数之间可以进行互化。
探索与发现
(2)分数、除法之间的关系。
a÷b=a/b(b不为“0”),除法中的被除数相当于分数中的分子,除法中的除数相当于分数中的分母。
探索与发现
(3)商不变的规律与分数基本性质的关系。
商不变的规律:被除数和除数同时扩大或缩小相同的倍数(0除外),商不变。
例如:8÷10=0.8
(8×2)÷(10×2)=0.8
(8÷2)÷(10÷2)=0.8
分数的基本性质:分子与分母同时扩大或缩小相同的倍数(0除外),分数的大小不变。
探索与发现
根据除法与分数的联系:除法中的被除数相当于分数中的分子,除法中的除数相当于分数中的分母,即商不变的规律与分数基本性质的原理相同。
探索与发现
百位
千位
个
万
亿
万位
十万位
百万位
千万位
亿位
十亿位
百亿位
千亿位
百分位
千分位
万分位
百
千
万
十万
百万
千万
亿
十亿
百亿
千亿
十
一(个)
百分之一
千分之一
万分之一
10
学以致用
03
学以致用
学以致用
5
2
5
3
2
1
2
1
8
5
8
3
3
1
3
2
学以致用
>
>
=
>
=
<
=
=
课后作业
04
感 谢 观 看
总 复 习
数的认识
第二课时 小数、分数、百分数
目 录
情景导学
1
探索与发现
2
学以致用
3
课后作业
4
情景导学
01
情景导学
用尽可能多的方式解释“ ”的含义。
把3个苹果平均分成4份,求每份有多少个苹果,用除法计算:3÷4= (个),每份是 个苹果。这里的 表示具体的数量。
探索与发现
02
探索与发现
把一个圆平均分成4份,其中的3份用分数表示是 。
把一个正方形平均分成4份,涂色部分占其中的一份,用分数表示是 ,3个 用 ×3= 。
探索与发现
红色彩带的长度是绿色彩带长度的 。
探索与发现
结合具体的例子说一说。
(1)小数、分数、百分数之间的关系。
(2)分数、除法之间的关系。
(3)商不变的规律与分数基本性质的关系。
探索与发现
(1)小数、分数、百分数之间的关系。
小数的意义:小数实际是十进制分数的另一种形式,十分之一、百分之一、千分之一……的分数都可以用小数表示,如:0.1、0.01、0.001……。
探索与发现
分数的意义:把单位“1”平均分成若干份,表示这样的一份或几份的数叫作分数。
分数可以表示两种含义:后面带计量单位可以表示一个具体的量,
如:一个菠萝重3/4 kg、一根绳子长1/4m;不带计量单位可以表示两个量的倍数关系,如:小明身高是小红身高的4/5。
探索与发现
百分数的意义:表示一个数是另一个数的百分之几的数叫作百分数。
百分数只能表示一个量是另一个量的百分之几,不能带上计量单位来表示具体的量。
如:六年级参加兴趣活动的同学占全年级人数的80%。
探索与发现
小数、分数、百分数之间可以进行互化。
探索与发现
(2)分数、除法之间的关系。
a÷b=a/b(b不为“0”),除法中的被除数相当于分数中的分子,除法中的除数相当于分数中的分母。
探索与发现
(3)商不变的规律与分数基本性质的关系。
商不变的规律:被除数和除数同时扩大或缩小相同的倍数(0除外),商不变。
例如:8÷10=0.8
(8×2)÷(10×2)=0.8
(8÷2)÷(10÷2)=0.8
分数的基本性质:分子与分母同时扩大或缩小相同的倍数(0除外),分数的大小不变。
探索与发现
根据除法与分数的联系:除法中的被除数相当于分数中的分子,除法中的除数相当于分数中的分母,即商不变的规律与分数基本性质的原理相同。
探索与发现
百位
千位
个
万
亿
万位
十万位
百万位
千万位
亿位
十亿位
百亿位
千亿位
百分位
千分位
万分位
百
千
万
十万
百万
千万
亿
十亿
百亿
千亿
十
一(个)
百分之一
千分之一
万分之一
10
学以致用
03
学以致用
学以致用
5
2
5
3
2
1
2
1
8
5
8
3
3
1
3
2
学以致用
>
>
=
>
=
<
=
=
课后作业
04
感 谢 观 看
