6.4.3.1余弦定理 (说课) 课件(共23张PPT)
文档属性
| 名称 | 6.4.3.1余弦定理 (说课) 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-29 07:46:41 | ||
图片预览








文档简介
(共23张PPT)
余弦定理
课堂教学部分
一、引言
我们知道,三角形两边和它们的夹角分别相等的两个三角形全等.这说明,给定两边及其夹角的三角形是唯一确定的. 也就是说,已知三角形两边及其夹角,其他的边、角都可以用这两边及其夹角来表示. 那么,表示的公式是什么?这就是本节课我们主要探讨的问题.
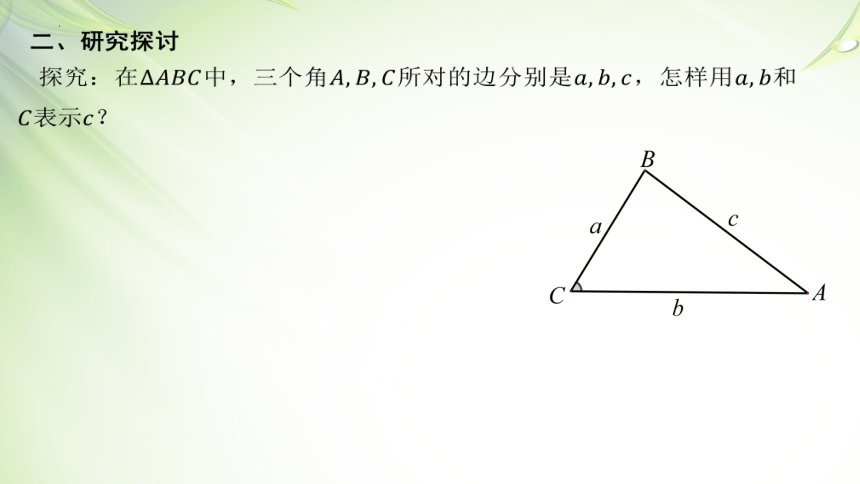
二、研究探讨
探究:在中,三个角所对的边分别是,怎样用和表示?
问题1 在中,记,,, 那么在中,用和表示的本质就是用和向量的夹角来表示,你能表示出来吗?
因为
故
所以
同理可得
解:
三、概念形成
通过以上探究,我们得到了三角形边角关系:
三角形任何一边的平方,等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍.
余弦定理
探究思考:你还能用其它方法证明余弦定理吗?
问题2 在问题1中我们是用向量的线性运算和数量积来得到余弦定理的,那你能否利用向量的坐标运算证明余弦定理呢?
解:如图所示,以点为坐标原点建立直角坐标系,
根据任意角三角函数的定义,
,
则有,
所以
同理可得
则有
解:当为直角时,根据勾股定理得
当为锐角时,如问题1(2)图,,
,
.
当为钝角时,如问题1(3)图,,
,
,
.
综上,一般情况时,都有
问题3 我们发现,当三角形其中一个角为时,余弦定理就是初中阶段所学 的勾股定理,那你能否用平面几何方法证明余弦定理呢
同理可得
四、概念深化
问题4 (1)根据余弦定理,我们可以从三角形已知的两条边及其夹角直接求出第三边,其余的两个角如何求呢?
根据余弦定理,可以得到下列推论
(2)一般地,三角形的三个角和它们的对边叫做三角形的元素. 已知三角形的几个元素求其它元素的过程叫做解三角形. 已知三角形的哪些元素,可以使用余弦定理及推论来解?
已知三角形两边及其夹角和已知三边,都可以可以使用余弦定理来解.
五、应用举例
例1 在中,已知,, ,解这个三角形(角度精确到,边长精确到1cm).
分析:这是已知三角形的两边及其夹角的解三角形问题,故先使用余弦定理求出第三边,然后根据推论求出其余的角.
解:由余弦定理,得
所以
根据余弦定理的推论,得
可得
所以.
计算器
练习 在中,,锐角满足,求(已知)
分析:由条件可求,再利用余弦定理及其推论可求出的值.
解:因为,且为锐角,
所以
由余弦定理,得
所以
进而
考虑,
,
又,故.
六、归纳总结
(2)余弦定理可以解决哪些解三角形问题?蕴含了什么思想?
(1)比较余弦定理的三种证法,总结其思想方法.
问题3
坐标法
向量法
几何直观,代数精确,向量兼具数与形,更加强大!
问题1
问题2
几何法
代数法
可以解决“SAS、SSS”问题,本质是方程的思想.
我国著名数学家华罗庚说过:
“数缺形时少直观,形少数时难入微;
数形结合百般好,隔离分家万事休”.
七、课后作业
教材第44页练习第1-3题.
教学阐述部分
教学内容及解析
学情分析
教学目标
教学过程设计
重难点的突破
【教学内容及解析】
(一)教学内容
余弦定理的推导;余弦定理及推论;利用余弦定理解三角形.
(二)教学内容解析
余弦定理是解决斜三角形问题的一个重要定理,是初中”勾股定理”内容的直接延拓,也是三角函数一般知识和平面向量知识在三角形中的具体应用。教材安排在向量的应用这章节,旨在通过向量的方法研究三角形边与角的数量关系,从而把初中阶段对三角形边与角的定性描述转化为定量计算。余弦定理与下一节的正弦定理成为解三角形问题的重要定理.
【学情分析】
一方面,学生在初中阶段已经知道:已知三角形的两边及夹角,那么这个三角形是唯一确定的,对此有一个定性的认识,不过还不能定量去描述它们的关系。另一方面,学生学习余弦定理之前已经学习了向量和三角函数等相关知识,具备自主探究推导余弦定理的知识储备.
教学目标:
1. 通过问题探究,学生能运用向量推导出余弦定理,发展学生的逻辑推理能力,达到逻辑推理核心素养水平一的要求;
2. 通过多种方法证明余弦定理,发展培养学生的数学思想方法;
3.通过解决简单的解三角形问题,巩固学生对余弦定理的理解与应用,达到数学运算核心素养水平一的要求.
【教学重难点】
重点:1.探究和证明余弦定理的过程;
2.运用余弦定理解三角形.
难点:余弦定理的证明.
【教学过程设计】
提出问题
问题1
数学背景
分层递进`
向量法
余弦定理
余弦定理的推论
解三角形
问题2
问题3
坐标法
几何法
【重难点突破】
问题1在中,记,,, 那么在中,用和表示的本质就是用和向量的夹角来表示,你能表示出来吗?
问题2 在问题1中我们是用向量的线性运算和数量积来得到余弦定理的,那你能否利用向量的坐标运算证明余弦定理呢?
问题3 我们发现,当三角形其中一个角为时,余弦定理就是初中阶段所学的勾股定理,那你能否用平面几何方法证明余弦定理呢?
【设计意图】学生刚学完向量,通过问题1的引导,可以得到问题1的解答,从而得到余弦定理.问题1的解答是利用向量的线性运算和数量积运算,向量还有坐运算,由此设计了问题2,帮助学生更全面的应用向量,在运算过程中需要注意B点坐标的求法.问题3的设置目的是鼓励学生建立数学知识之间的联系,培养学生解题思维的灵活性,比较起来也更进一步说明了向量强大之处!
谢谢
余弦定理
课堂教学部分
一、引言
我们知道,三角形两边和它们的夹角分别相等的两个三角形全等.这说明,给定两边及其夹角的三角形是唯一确定的. 也就是说,已知三角形两边及其夹角,其他的边、角都可以用这两边及其夹角来表示. 那么,表示的公式是什么?这就是本节课我们主要探讨的问题.
二、研究探讨
探究:在中,三个角所对的边分别是,怎样用和表示?
问题1 在中,记,,, 那么在中,用和表示的本质就是用和向量的夹角来表示,你能表示出来吗?
因为
故
所以
同理可得
解:
三、概念形成
通过以上探究,我们得到了三角形边角关系:
三角形任何一边的平方,等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍.
余弦定理
探究思考:你还能用其它方法证明余弦定理吗?
问题2 在问题1中我们是用向量的线性运算和数量积来得到余弦定理的,那你能否利用向量的坐标运算证明余弦定理呢?
解:如图所示,以点为坐标原点建立直角坐标系,
根据任意角三角函数的定义,
,
则有,
所以
同理可得
则有
解:当为直角时,根据勾股定理得
当为锐角时,如问题1(2)图,,
,
.
当为钝角时,如问题1(3)图,,
,
,
.
综上,一般情况时,都有
问题3 我们发现,当三角形其中一个角为时,余弦定理就是初中阶段所学 的勾股定理,那你能否用平面几何方法证明余弦定理呢
同理可得
四、概念深化
问题4 (1)根据余弦定理,我们可以从三角形已知的两条边及其夹角直接求出第三边,其余的两个角如何求呢?
根据余弦定理,可以得到下列推论
(2)一般地,三角形的三个角和它们的对边叫做三角形的元素. 已知三角形的几个元素求其它元素的过程叫做解三角形. 已知三角形的哪些元素,可以使用余弦定理及推论来解?
已知三角形两边及其夹角和已知三边,都可以可以使用余弦定理来解.
五、应用举例
例1 在中,已知,, ,解这个三角形(角度精确到,边长精确到1cm).
分析:这是已知三角形的两边及其夹角的解三角形问题,故先使用余弦定理求出第三边,然后根据推论求出其余的角.
解:由余弦定理,得
所以
根据余弦定理的推论,得
可得
所以.
计算器
练习 在中,,锐角满足,求(已知)
分析:由条件可求,再利用余弦定理及其推论可求出的值.
解:因为,且为锐角,
所以
由余弦定理,得
所以
进而
考虑,
,
又,故.
六、归纳总结
(2)余弦定理可以解决哪些解三角形问题?蕴含了什么思想?
(1)比较余弦定理的三种证法,总结其思想方法.
问题3
坐标法
向量法
几何直观,代数精确,向量兼具数与形,更加强大!
问题1
问题2
几何法
代数法
可以解决“SAS、SSS”问题,本质是方程的思想.
我国著名数学家华罗庚说过:
“数缺形时少直观,形少数时难入微;
数形结合百般好,隔离分家万事休”.
七、课后作业
教材第44页练习第1-3题.
教学阐述部分
教学内容及解析
学情分析
教学目标
教学过程设计
重难点的突破
【教学内容及解析】
(一)教学内容
余弦定理的推导;余弦定理及推论;利用余弦定理解三角形.
(二)教学内容解析
余弦定理是解决斜三角形问题的一个重要定理,是初中”勾股定理”内容的直接延拓,也是三角函数一般知识和平面向量知识在三角形中的具体应用。教材安排在向量的应用这章节,旨在通过向量的方法研究三角形边与角的数量关系,从而把初中阶段对三角形边与角的定性描述转化为定量计算。余弦定理与下一节的正弦定理成为解三角形问题的重要定理.
【学情分析】
一方面,学生在初中阶段已经知道:已知三角形的两边及夹角,那么这个三角形是唯一确定的,对此有一个定性的认识,不过还不能定量去描述它们的关系。另一方面,学生学习余弦定理之前已经学习了向量和三角函数等相关知识,具备自主探究推导余弦定理的知识储备.
教学目标:
1. 通过问题探究,学生能运用向量推导出余弦定理,发展学生的逻辑推理能力,达到逻辑推理核心素养水平一的要求;
2. 通过多种方法证明余弦定理,发展培养学生的数学思想方法;
3.通过解决简单的解三角形问题,巩固学生对余弦定理的理解与应用,达到数学运算核心素养水平一的要求.
【教学重难点】
重点:1.探究和证明余弦定理的过程;
2.运用余弦定理解三角形.
难点:余弦定理的证明.
【教学过程设计】
提出问题
问题1
数学背景
分层递进`
向量法
余弦定理
余弦定理的推论
解三角形
问题2
问题3
坐标法
几何法
【重难点突破】
问题1在中,记,,, 那么在中,用和表示的本质就是用和向量的夹角来表示,你能表示出来吗?
问题2 在问题1中我们是用向量的线性运算和数量积来得到余弦定理的,那你能否利用向量的坐标运算证明余弦定理呢?
问题3 我们发现,当三角形其中一个角为时,余弦定理就是初中阶段所学的勾股定理,那你能否用平面几何方法证明余弦定理呢?
【设计意图】学生刚学完向量,通过问题1的引导,可以得到问题1的解答,从而得到余弦定理.问题1的解答是利用向量的线性运算和数量积运算,向量还有坐运算,由此设计了问题2,帮助学生更全面的应用向量,在运算过程中需要注意B点坐标的求法.问题3的设置目的是鼓励学生建立数学知识之间的联系,培养学生解题思维的灵活性,比较起来也更进一步说明了向量强大之处!
谢谢
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
