第十章 概率(章末小结) 课件(共18张PPT)
文档属性
| 名称 | 第十章 概率(章末小结) 课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 776.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-29 10:23:12 | ||
图片预览






文档简介
(共18张PPT)
章末小结
必修第二册 第十章《概率》
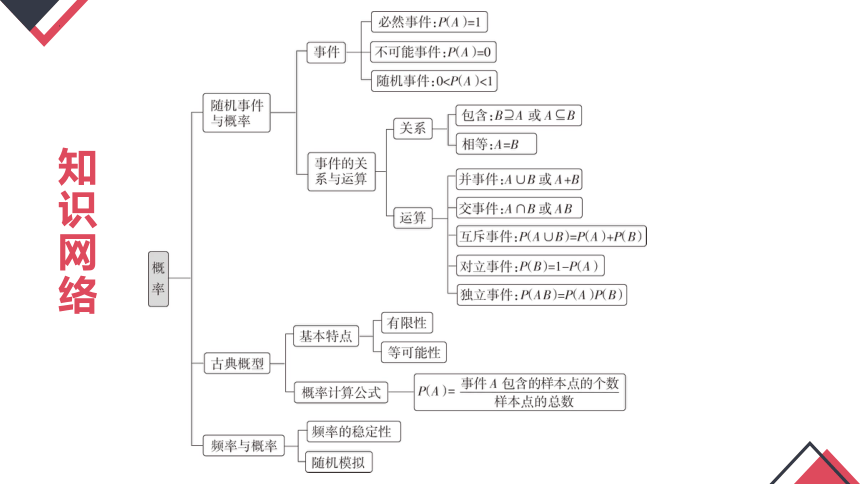
知识网络
知识梳理——1.随机试验
1.对随机现象的实现和对它的观察称为随机试验,简称试验.通常用字母E表示.
2.随机试验的特点:
(1)试验可以在相同条件下重复进行;
(2)试验的所有可能结果是明确可知的,并且不止一个;
(3)每次试验总是恰好出现这些可能结果中的一个,但事先不能确定出现哪一个结果.
可重复性
可预知性
随机性
3.随机试验E的每个可能的基本结果称为样本点,用ω表示.
4.所有样本点的集合称为试验E的样本空间,用Ω表示.
5.若一个随机试验有n个可能结果ω1,ω2,…,ωn,则称样本空间Ω={ω1,ω2,…,ωn}为有限样本空间.
6.随机实验中每个随机事件都可以用这个试验的样本空间的子集来表示.
7.将样本空间Ω的子集称为随机事件,简称事件,用大写字母A,B,C…表示;
8.只包含一个样本点的事件称为基本事件;
知识梳理——1.随机试验
1.在列出样本点时,应先确定样本点是否与顺序有关.
写样本空间的样本点时,要按一定顺序和规律写,做到不充不漏.
2.写出试验的样本空间的方法:
(1)列举法:适合于较简单的问题.
(2)列表法:适合求较复杂问题中的样本点数.
(3)树形图法:适合较复杂问题中基本事件的探求.
样本点的计数问题
知识梳理——2.事件的分类
在每次试验中,当且仅当A中某个样本点出现时,称为事件A发生.
①Ω包含了所有的样本点,在每次试验中总有一个样本点发生,所以Ω总会发生,我们称Ω为必然事件.
②空集 不包含任何样本点,在每次试验中都不会发生,我们称空集 为不可能事件.
注:必然事件与不可能事件不具有随机性.
将必然事件和不可能事件作为随机事件的两个极端情形.
每个事件都是样本空间Ω的一个子集.
知识梳理——3.事件的关系和运算
事件A包含于事件B 事件A发生,则事件B一定发生 A B P(A)≤P(B)
事件A与B的并(和)事件 事件A与事件B至少有一个发生 A∪B(或A+B)
P(A∪B)=P(A)+P(B)-P(A∩B)
事件A与B的交(积)事件 事件A与事件B同时发生 A∩B(或AB)
事件A与事件B互斥 事件A与事件B不会同时发生 A∩B=
P(A∪B)=P(A)+P(B)
事件A与事件B互相对立 事件A与事件B在有且仅有一个发生 A∪B=Ω且A∩B=
P(A)+P()=1
事件A与事件B相互独立 事件A发生与否不影响事件B发生的概率 P(AB)=P(A)P(B)
互为对立事件一定是互斥事件.
互斥事件不一定互为对立.
知识梳理——3.事件的关系和运算
如:A=“点数为1”,B=“点数为奇数”,则_______
如:A=“点数为1或2”,B=“点数不大于2”,则______
①若事件A发生,则事件B一定发生,则称事件B包含事件A
(或事件A包含于事件B),记作B A(或A B).
②若事件B包含事件A,事件A也包含事件B,即B A且A B,
则称事件A与事件B相等,记作A=B.
Ω
③事件A与事件B至少有一个发生,且事件C中的样本点或者在事件A中,或者在事件B中,则称事件C为事件A与事件B的并事件(或和事件),记作A∪B(或A+B).
A B
A=B
C=A∪B
Ω
Ω
如: C=“点数不大于3”,A=“点数为1或2”,B=“点数为2或3”,则_______
知识梳理——3.事件的关系和运算
④事件A与事件B同时发生,且事件C中的样本点既在事件A中,又在事件B中,则称事件C为事件A与事件B的交事件(或积事件),记作A∩B(或AB).
C=A∩B
{1,2}∩{2,3}={2}
注:可以定义多个事件的(并)和事件、(交)积事件.
如:对于三个事件A,B,C,
A∪B∪C发生当且仅当A,B,C至少有一个发生;
A∩B∩C发生当且仅当A,B,C同时发生.
Ω
如: C=“点数为2”,A=“点数为1或2”,B=“点数为2或3”,则_______
知识梳理——3.事件的关系和运算
定义法判断事件是否相互独立
对任意两个事件A与B,如果 P(AB)=P(A)P(B)成立,
则称事件A与事件B相互独立,简称为独立.
若事件A发生与否不影响事件B发生的概率,
则事件A与B相互独立,从而有P(AB)=P(A)P(B)
直接法判断事件是否相互独立
计算积事件的概率(前提:A,B独立)
注:①必然事件Ω、不可能事件 与任意事件A相互独立.
②若事件A,B相互独立,则A与B、A与B、A与B也相互独立.
③三个事件A、B、C两两互斥,则P(A1∪A2∪A3)=P(A1)+P(A2)+P(A3)成立,
但三个事件A、B、C两两独立时,P(ABC)=P(A)P(B)P(C)一般不成立.
知识梳理——4.古典概型
古典概型的特点:
①有限性:样本空间的样本点只有有限个;
②等可能性:每个样本点发生的可能性相等;
一般地,设试验E是古典概型,
样本空间Ω包含n个样本点,事件A包含其中的k个样本点,
则定义事件A的概率.
其中,n(A)和n(Ω)分别表示事件A和样本空间Ω包含的样本点个数。
知识梳理——5.频率与概率
大量试验表明,在任何确定次数的随机试验中,
一个随机事件A发生的频率具有随机性.
一般地,随着试验次数n的增大,频率偏离概率的幅度会缩小,
即事件A发生的频率fn(A)会逐渐稳定于事件A发生的概率 P(A) ,
称频率的这个性质为频率的稳定性 .
因此,我们可以用频率fn(A)估计概率P(A).
知识梳理——5.频率与概率
区别:频率是一个变量,随着试验次数的变化而变化,具有随机性;
概率是一个定值,是某事件的固有属性,不随试验次数的变化而变化.
联系:频率是概率的试验值,一般会随试验次数的增加逐渐稳定于概率附近;
概率是频率的稳定值,在实际中当次数足够多时,可用频率估计概率.
小概率事件(概率接近于0)很少发生,但不代表一定不发生;
大概率事件(概率接近于1)经常发生,但不代表一定发生.
知识梳理——6.随机模拟
用频率估计概率,需要做大量的重复试验.
我们知道,利用计算器或计算机软件可以产生随机数.
实际上,我们也可以根据不同的随机试验构建相应的随机数模拟试验,
这样就可以快速地进行大量重复试验了.
由试验产生的随机数:
例如,我们要产生0~9之间的整数随机数,可像彩票摇奖那样,把10个质地和大小相同的号码球放入摇奖器中,充分搅拌后摇出一个球,这个球上的号码称为随机数.
计算机产生的随机数:
利用计算机产生随机数是按照确定的算法产生的数,具有周期性,因此我们把利用计算机产生的随机数称为伪随机数.
RANDBETWEEN(1,n)函数表示产生于1~n范围内的整数随机数.
方法提炼——判断事件是否相互独立
3.转化法:事件A与事件B是否相互独立,与事件A与 , 与B, 与 是否具有独立性可互相转化.
1.直接法:直接判断一个事件发生与否是否影响另一事件发生的概率.
2.定义法:判断P(AB)=P(A)P(B)是否成立.
方法提炼——正难则反
灵活应用对立事件的概率关系P(A)+P()=1简化问题,
是求解概率问题最常用的方法.
例.甲、乙两名射击运动员进行射击比赛,甲的中靶概率为0.8,
乙的中靶概率为0.9,求至少有一人中靶的概率.
析:设A=“甲中靶”,B=“乙中靶”,则A=“甲脱靶”,B=“乙脱靶”.
由于两个人射击的结果互不影响,∴A与B相互独立,
且A与B,A与B,A与B都相互独立.
方法提炼——化归与转化
化繁为简.将复杂事件的概率转化为简单事件的概率,即寻找所求事件与已知事件之间的关系.所求事件分几类(考虑加法公式转化为互斥事件)还是分几步组成(考虑乘法公式转化为相互独立事件).
P241-例12.为了推广一 种饮料,某饮料生产企业开展了有奖促销活动:
将6罐这种饮料装一箱,每箱中都放置2罐能够中奖的饮料.
若从一箱中随机抽出2罐,能中奖的概率为多少
方法提炼——整合思想
在解决综合问题时,应对图表进行观察、分析、提炼,挖掘出图表所给予的有用信息,排除无关数据的干扰,进而抓住问题的实质,达到求解的目的.
END
章末小结
必修第二册 第十章《概率》
知识网络
知识梳理——1.随机试验
1.对随机现象的实现和对它的观察称为随机试验,简称试验.通常用字母E表示.
2.随机试验的特点:
(1)试验可以在相同条件下重复进行;
(2)试验的所有可能结果是明确可知的,并且不止一个;
(3)每次试验总是恰好出现这些可能结果中的一个,但事先不能确定出现哪一个结果.
可重复性
可预知性
随机性
3.随机试验E的每个可能的基本结果称为样本点,用ω表示.
4.所有样本点的集合称为试验E的样本空间,用Ω表示.
5.若一个随机试验有n个可能结果ω1,ω2,…,ωn,则称样本空间Ω={ω1,ω2,…,ωn}为有限样本空间.
6.随机实验中每个随机事件都可以用这个试验的样本空间的子集来表示.
7.将样本空间Ω的子集称为随机事件,简称事件,用大写字母A,B,C…表示;
8.只包含一个样本点的事件称为基本事件;
知识梳理——1.随机试验
1.在列出样本点时,应先确定样本点是否与顺序有关.
写样本空间的样本点时,要按一定顺序和规律写,做到不充不漏.
2.写出试验的样本空间的方法:
(1)列举法:适合于较简单的问题.
(2)列表法:适合求较复杂问题中的样本点数.
(3)树形图法:适合较复杂问题中基本事件的探求.
样本点的计数问题
知识梳理——2.事件的分类
在每次试验中,当且仅当A中某个样本点出现时,称为事件A发生.
①Ω包含了所有的样本点,在每次试验中总有一个样本点发生,所以Ω总会发生,我们称Ω为必然事件.
②空集 不包含任何样本点,在每次试验中都不会发生,我们称空集 为不可能事件.
注:必然事件与不可能事件不具有随机性.
将必然事件和不可能事件作为随机事件的两个极端情形.
每个事件都是样本空间Ω的一个子集.
知识梳理——3.事件的关系和运算
事件A包含于事件B 事件A发生,则事件B一定发生 A B P(A)≤P(B)
事件A与B的并(和)事件 事件A与事件B至少有一个发生 A∪B(或A+B)
P(A∪B)=P(A)+P(B)-P(A∩B)
事件A与B的交(积)事件 事件A与事件B同时发生 A∩B(或AB)
事件A与事件B互斥 事件A与事件B不会同时发生 A∩B=
P(A∪B)=P(A)+P(B)
事件A与事件B互相对立 事件A与事件B在有且仅有一个发生 A∪B=Ω且A∩B=
P(A)+P()=1
事件A与事件B相互独立 事件A发生与否不影响事件B发生的概率 P(AB)=P(A)P(B)
互为对立事件一定是互斥事件.
互斥事件不一定互为对立.
知识梳理——3.事件的关系和运算
如:A=“点数为1”,B=“点数为奇数”,则_______
如:A=“点数为1或2”,B=“点数不大于2”,则______
①若事件A发生,则事件B一定发生,则称事件B包含事件A
(或事件A包含于事件B),记作B A(或A B).
②若事件B包含事件A,事件A也包含事件B,即B A且A B,
则称事件A与事件B相等,记作A=B.
Ω
③事件A与事件B至少有一个发生,且事件C中的样本点或者在事件A中,或者在事件B中,则称事件C为事件A与事件B的并事件(或和事件),记作A∪B(或A+B).
A B
A=B
C=A∪B
Ω
Ω
如: C=“点数不大于3”,A=“点数为1或2”,B=“点数为2或3”,则_______
知识梳理——3.事件的关系和运算
④事件A与事件B同时发生,且事件C中的样本点既在事件A中,又在事件B中,则称事件C为事件A与事件B的交事件(或积事件),记作A∩B(或AB).
C=A∩B
{1,2}∩{2,3}={2}
注:可以定义多个事件的(并)和事件、(交)积事件.
如:对于三个事件A,B,C,
A∪B∪C发生当且仅当A,B,C至少有一个发生;
A∩B∩C发生当且仅当A,B,C同时发生.
Ω
如: C=“点数为2”,A=“点数为1或2”,B=“点数为2或3”,则_______
知识梳理——3.事件的关系和运算
定义法判断事件是否相互独立
对任意两个事件A与B,如果 P(AB)=P(A)P(B)成立,
则称事件A与事件B相互独立,简称为独立.
若事件A发生与否不影响事件B发生的概率,
则事件A与B相互独立,从而有P(AB)=P(A)P(B)
直接法判断事件是否相互独立
计算积事件的概率(前提:A,B独立)
注:①必然事件Ω、不可能事件 与任意事件A相互独立.
②若事件A,B相互独立,则A与B、A与B、A与B也相互独立.
③三个事件A、B、C两两互斥,则P(A1∪A2∪A3)=P(A1)+P(A2)+P(A3)成立,
但三个事件A、B、C两两独立时,P(ABC)=P(A)P(B)P(C)一般不成立.
知识梳理——4.古典概型
古典概型的特点:
①有限性:样本空间的样本点只有有限个;
②等可能性:每个样本点发生的可能性相等;
一般地,设试验E是古典概型,
样本空间Ω包含n个样本点,事件A包含其中的k个样本点,
则定义事件A的概率.
其中,n(A)和n(Ω)分别表示事件A和样本空间Ω包含的样本点个数。
知识梳理——5.频率与概率
大量试验表明,在任何确定次数的随机试验中,
一个随机事件A发生的频率具有随机性.
一般地,随着试验次数n的增大,频率偏离概率的幅度会缩小,
即事件A发生的频率fn(A)会逐渐稳定于事件A发生的概率 P(A) ,
称频率的这个性质为频率的稳定性 .
因此,我们可以用频率fn(A)估计概率P(A).
知识梳理——5.频率与概率
区别:频率是一个变量,随着试验次数的变化而变化,具有随机性;
概率是一个定值,是某事件的固有属性,不随试验次数的变化而变化.
联系:频率是概率的试验值,一般会随试验次数的增加逐渐稳定于概率附近;
概率是频率的稳定值,在实际中当次数足够多时,可用频率估计概率.
小概率事件(概率接近于0)很少发生,但不代表一定不发生;
大概率事件(概率接近于1)经常发生,但不代表一定发生.
知识梳理——6.随机模拟
用频率估计概率,需要做大量的重复试验.
我们知道,利用计算器或计算机软件可以产生随机数.
实际上,我们也可以根据不同的随机试验构建相应的随机数模拟试验,
这样就可以快速地进行大量重复试验了.
由试验产生的随机数:
例如,我们要产生0~9之间的整数随机数,可像彩票摇奖那样,把10个质地和大小相同的号码球放入摇奖器中,充分搅拌后摇出一个球,这个球上的号码称为随机数.
计算机产生的随机数:
利用计算机产生随机数是按照确定的算法产生的数,具有周期性,因此我们把利用计算机产生的随机数称为伪随机数.
RANDBETWEEN(1,n)函数表示产生于1~n范围内的整数随机数.
方法提炼——判断事件是否相互独立
3.转化法:事件A与事件B是否相互独立,与事件A与 , 与B, 与 是否具有独立性可互相转化.
1.直接法:直接判断一个事件发生与否是否影响另一事件发生的概率.
2.定义法:判断P(AB)=P(A)P(B)是否成立.
方法提炼——正难则反
灵活应用对立事件的概率关系P(A)+P()=1简化问题,
是求解概率问题最常用的方法.
例.甲、乙两名射击运动员进行射击比赛,甲的中靶概率为0.8,
乙的中靶概率为0.9,求至少有一人中靶的概率.
析:设A=“甲中靶”,B=“乙中靶”,则A=“甲脱靶”,B=“乙脱靶”.
由于两个人射击的结果互不影响,∴A与B相互独立,
且A与B,A与B,A与B都相互独立.
方法提炼——化归与转化
化繁为简.将复杂事件的概率转化为简单事件的概率,即寻找所求事件与已知事件之间的关系.所求事件分几类(考虑加法公式转化为互斥事件)还是分几步组成(考虑乘法公式转化为相互独立事件).
P241-例12.为了推广一 种饮料,某饮料生产企业开展了有奖促销活动:
将6罐这种饮料装一箱,每箱中都放置2罐能够中奖的饮料.
若从一箱中随机抽出2罐,能中奖的概率为多少
方法提炼——整合思想
在解决综合问题时,应对图表进行观察、分析、提炼,挖掘出图表所给予的有用信息,排除无关数据的干扰,进而抓住问题的实质,达到求解的目的.
END
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
