整数指数幂[下学期]
图片预览






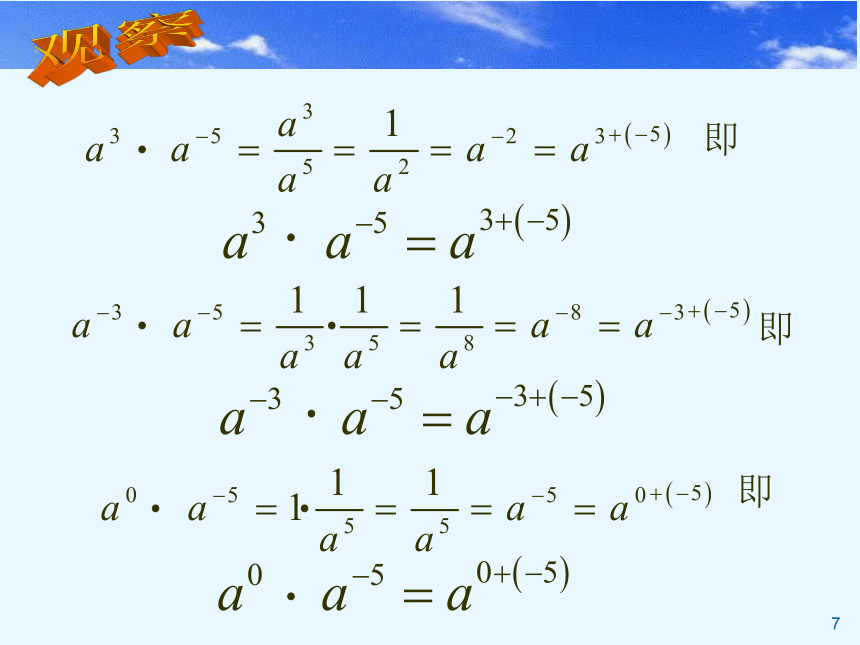
文档简介
课件17张PPT。北 师 大? 八 年 级《 数 学 ( 下 ) 》课首
第十六章 分 式 新人教版 ? 八 年 级 《 数 学 ( 下 ) 》16.2.3 整数指数幂16复习正整数指数幂有以下运算性质:(1)am·an=am+n (a≠0 m、n为正整数)
(2)(am)n=amn (a≠0 m、n为正整数)
(3)(ab)n=anbn (a,b≠0 m、n为正整数)
(4)am÷an=am-n (a≠0 m、n为正整数且m>n)
(5) ( b≠0 ,n是正整数)
当a≠0时,a0=1。(0指数幂的运算)(6)思考:例如:练习1、把下列负整数指数幂写成分式的形式,把分式写成负整数指数幂的形式:am=am (m是正整数)1 (m=0)(m是负整数)(1)32=_____, 30=___, 3-2=_____;
(2)(-3)2=____,(-3)0=___,(-3)-2=_____;
(3)b2=_____, b0=____, b-2=____(b≠0).练习91911即即即观察归纳归纳: 随着指数的取值范围由正整数推广到全体整数,
前面提到的幂的运算性质也推广到整数指数幂。即m、n为整数m、n为整数n为整数n为整数m、n为整数( )( )( )( )( )例题应用
例1 计算(1)(2)(3);;.跟踪练习:
(1) x2y-3(x-1y)3;
(2) (2ab2c-3)-2÷(a-2b)32 . 计算下列各式,并把结果化为只含正整数指数的形式(a,b均不为0):(1);(2);(3).小结:
本节课主要学习了负整数指数幂的意义和整数
指数幂的运算性质,即指数幂运算法则的适用范围
由正整数扩大到全体整数。小结:本节课你的收获是什么?课堂达标测试基础题:1.计算:
(a+b)m+1·(a+b)n-1; (2) (-a2b)2·(-a2b3)3÷(-ab4)5
(3) (x3)2÷(x2)4·x0
(4) (-1.8x4y2z3) ÷(-0.2x2y4z) ÷(-1/3xyz)提高题:3.计算:xn+2·xn-2÷(x2)3n-3;4.已知:10m=5,10n=4,求102m-3n.5.探索规律:31=3,个位数字是3;32=9,个位数字式9;33=27,个位数字是7;34=81,个位数字是1;35=243,个位数字是3;36=729,个位数字是9;……那么,37的个位数字是______,320的个位数字是______。兴趣探索小结(1)n是正整数时, a-n属于分式。并且(a≠0)
第十六章 分 式 新人教版 ? 八 年 级 《 数 学 ( 下 ) 》16.2.3 整数指数幂16复习正整数指数幂有以下运算性质:(1)am·an=am+n (a≠0 m、n为正整数)
(2)(am)n=amn (a≠0 m、n为正整数)
(3)(ab)n=anbn (a,b≠0 m、n为正整数)
(4)am÷an=am-n (a≠0 m、n为正整数且m>n)
(5) ( b≠0 ,n是正整数)
当a≠0时,a0=1。(0指数幂的运算)(6)思考:例如:练习1、把下列负整数指数幂写成分式的形式,把分式写成负整数指数幂的形式:am=am (m是正整数)1 (m=0)(m是负整数)(1)32=_____, 30=___, 3-2=_____;
(2)(-3)2=____,(-3)0=___,(-3)-2=_____;
(3)b2=_____, b0=____, b-2=____(b≠0).练习91911即即即观察归纳归纳: 随着指数的取值范围由正整数推广到全体整数,
前面提到的幂的运算性质也推广到整数指数幂。即m、n为整数m、n为整数n为整数n为整数m、n为整数( )( )( )( )( )例题应用
例1 计算(1)(2)(3);;.跟踪练习:
(1) x2y-3(x-1y)3;
(2) (2ab2c-3)-2÷(a-2b)32 . 计算下列各式,并把结果化为只含正整数指数的形式(a,b均不为0):(1);(2);(3).小结:
本节课主要学习了负整数指数幂的意义和整数
指数幂的运算性质,即指数幂运算法则的适用范围
由正整数扩大到全体整数。小结:本节课你的收获是什么?课堂达标测试基础题:1.计算:
(a+b)m+1·(a+b)n-1; (2) (-a2b)2·(-a2b3)3÷(-ab4)5
(3) (x3)2÷(x2)4·x0
(4) (-1.8x4y2z3) ÷(-0.2x2y4z) ÷(-1/3xyz)提高题:3.计算:xn+2·xn-2÷(x2)3n-3;4.已知:10m=5,10n=4,求102m-3n.5.探索规律:31=3,个位数字是3;32=9,个位数字式9;33=27,个位数字是7;34=81,个位数字是1;35=243,个位数字是3;36=729,个位数字是9;……那么,37的个位数字是______,320的个位数字是______。兴趣探索小结(1)n是正整数时, a-n属于分式。并且(a≠0)
