第十一章 图形的全等 复习课[下学期]
文档属性
| 名称 | 第十一章 图形的全等 复习课[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 460.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-03-03 20:03:00 | ||
图片预览

文档简介
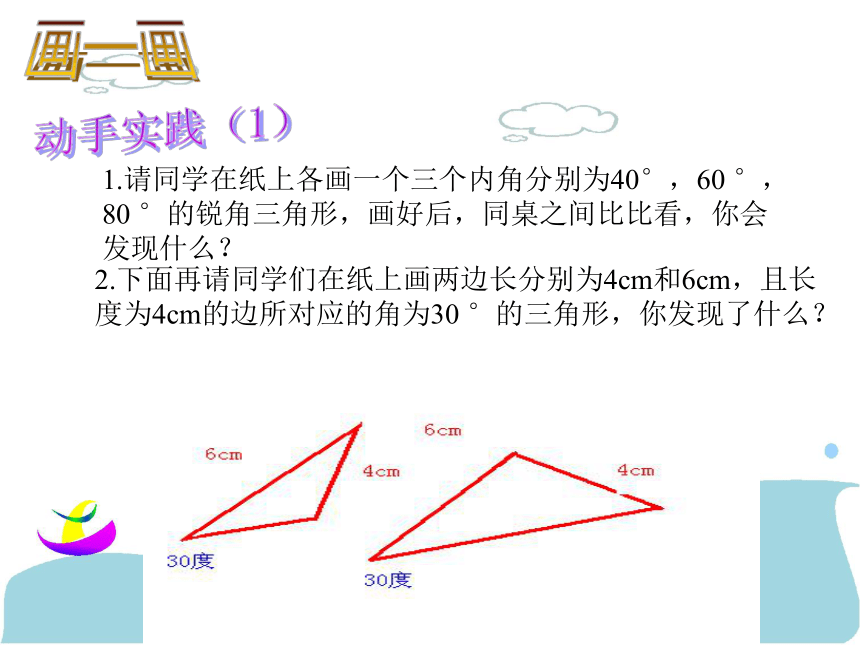
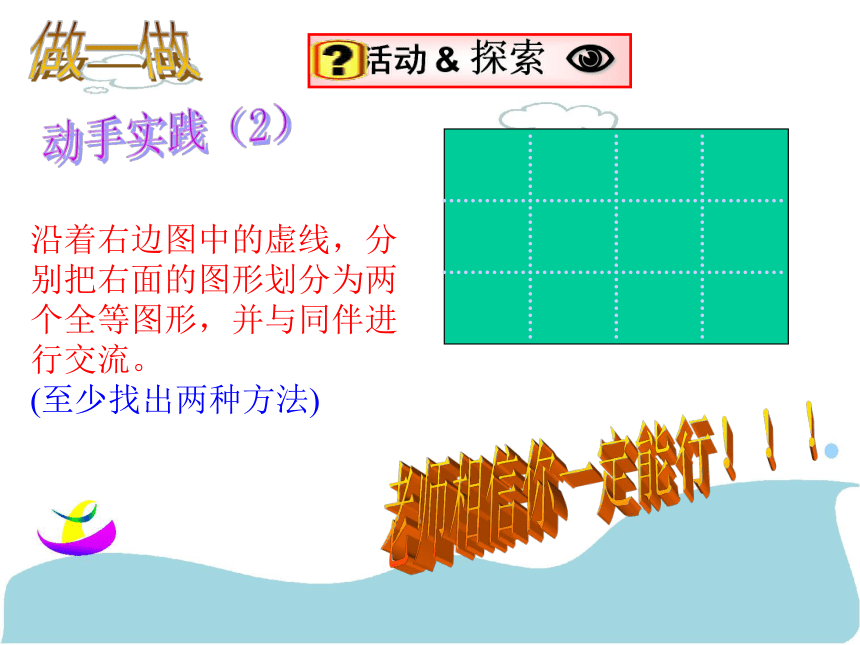
课件14张PPT。图形全等复习(1) 画一画1.请同学在纸上各画一个三个内角分别为40°,60 °,80 °的锐角三角形,画好后,同桌之间比比看,你会发现什么?2.下面再请同学们在纸上画两边长分别为4cm和6cm,且长度为4cm的边所对应的角为30 °的三角形,你发现了什么?动手实践(1) 动手实践(2)做一做沿着右边图中的虚线,分别把右面的图形划分为两个全等图形,并与同伴进行交流。
(至少找出两种方法)
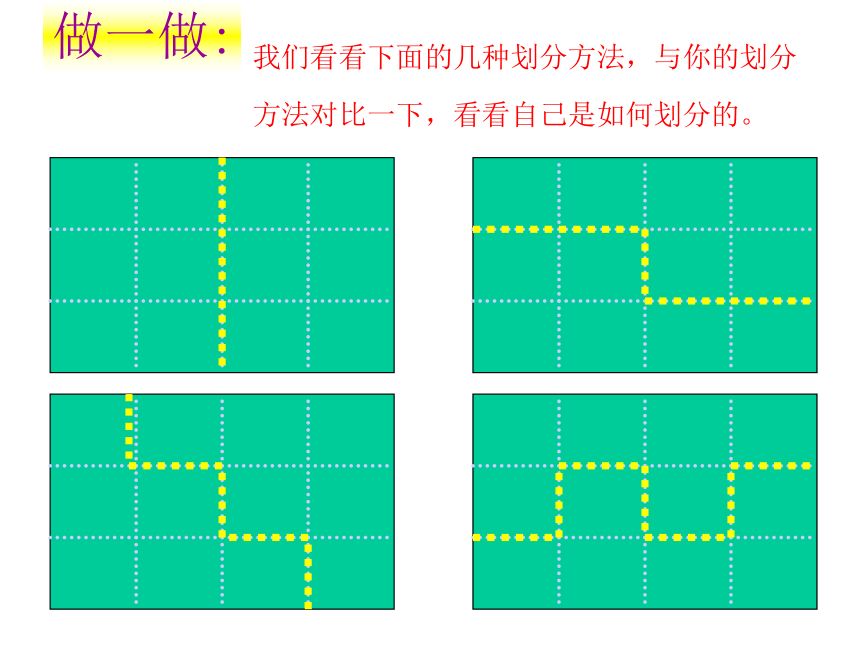
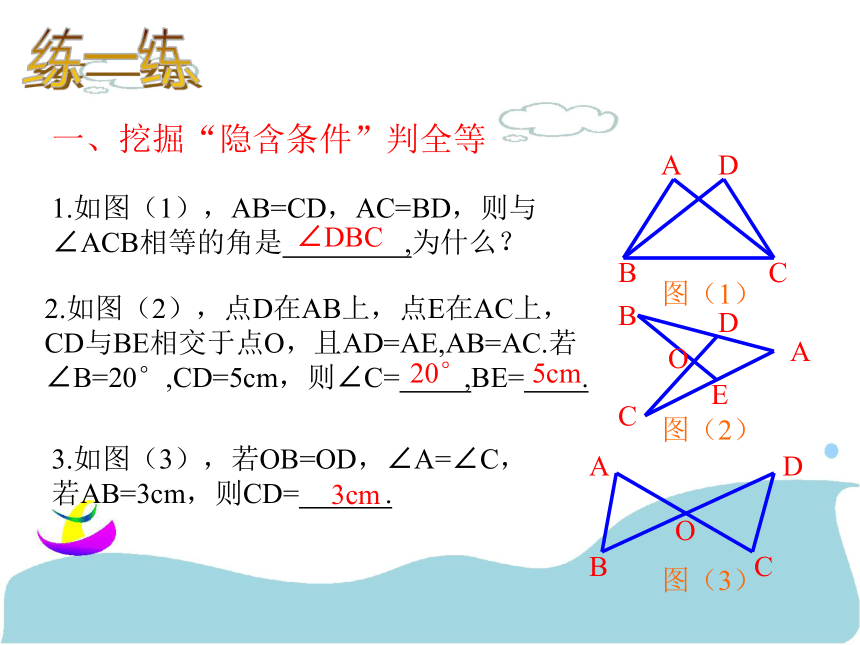
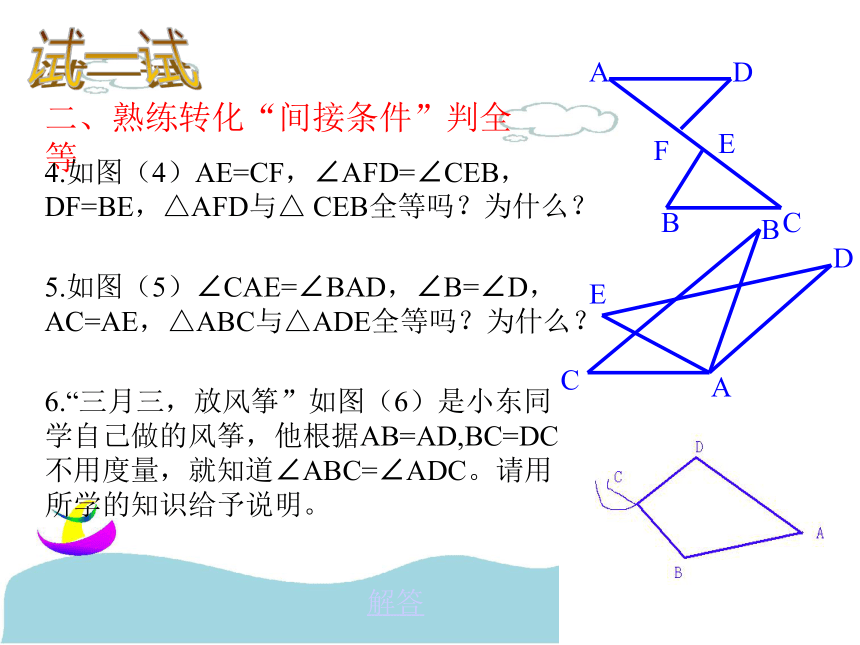
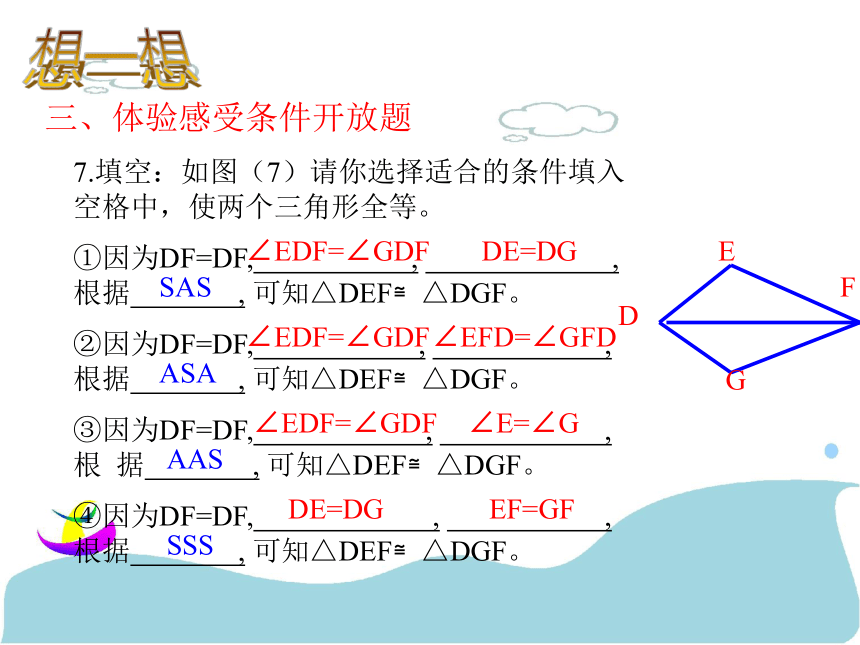
老师相信你一定能行!!!做一做:我们看看下面的几种划分方法,与你的划分方法对比一下,看看自己是如何划分的。图形一划分方法练一练一、挖掘“隐含条件”判全等1.如图(1),AB=CD,AC=BD,则与∠ACB相等的角是 ,为什么? 2.如图(2),点D在AB上,点E在AC上,CD与BE相交于点O,且AD=AE,AB=AC.若∠B=20°,CD=5cm,则∠C= ,BE= .3.如图(3),若OB=OD,∠A=∠C,若AB=3cm,则CD= . ADBC图(1)BCODEA图(2)ADBCO图(3)∠DBC20°5cm3cm试一试二、熟练转化“间接条件”判全等4.如图(4)AE=CF,∠AFD=∠CEB,DF=BE,△AFD与△ CEB全等吗?为什么?5.如图(5)∠CAE=∠BAD,∠B=∠D,AC=AE,△ABC与△ADE全等吗?为什么?6.“三月三,放风筝”如图(6)是小东同学自己做的风筝,他根据AB=AD,BC=DC,不用度量,就知道∠ABC=∠ADC。请用所学的知识给予说明。ADBCFEACEBD解答想一想三、体验感受条件开放题7.填空:如图(7)请你选择适合的条件填入空格中,使两个三角形全等。
①因为DF=DF, , ,根据 , 可知△DEF≌△DGF。
②因为DF=DF, , ,根据 , 可知△DEF≌△DGF。
③因为DF=DF, , ,根 据 , 可知△DEF≌△DGF。
④因为DF=DF, , ,根据 , 可知△DEF≌△DGF。EGDFDE=DG∠EDF=∠GDFSAS∠EDF=∠GDF∠EFD=∠GFDASA∠EDF=∠GDF∠E=∠GAASDE=DGEF=GFSSS议一议四、体验感受结论开放题8.如图(8)△ABE≌△ACD,由此你能得到什么结论?(越多越好)ABCDE睿智点心五、探究合作,数学好玩例⒌如图,等腰直角△ABC的直角顶点C在直线m上,AD⊥m,BE⊥m,垂足分别为D、E.
●试探索AD、BE、DE的大小关系
数学好玩OK“学好几何,必须过三关:语言关、符号关、作图关”可见,准确作图是学好几何的基础,而准确画出一个角的角平分线是我们接触到的几何基本作图之一。从教材上,同学们知道了“工人师傅利用角尺”和“尺规”作一个角的平分线。作为我们同学,没有“角尺”,可能还有部分同学没有圆规。此时,较准确地画出一个角的平分线可能就有困难了。难道我们不用量角器、“角尺”和圆规就没有办法作一个角的平分线了吗?聪明的你,拿出刻度尺或三角板画下图∠AOB的角平分线,试一试,看谁先完成!OAB 举例说明全等三角形与生活的密切联系,与同学交流数学与生活学习反思●我会了…
●我对了…
●还有… …谢谢合作4.如图(4)AE=CF,∠AFD=∠CEB,DF=BE,△AFD与△ CEB全等吗?为什么?解:∵AE=CFADBCFE∴AE-FE=CF-EF即AF=CE又∵ ∠AFD=∠CEB,
DF=BE
根据“SAS”,可以得到△AFD≌△CEB返
(至少找出两种方法)
老师相信你一定能行!!!做一做:我们看看下面的几种划分方法,与你的划分方法对比一下,看看自己是如何划分的。图形一划分方法练一练一、挖掘“隐含条件”判全等1.如图(1),AB=CD,AC=BD,则与∠ACB相等的角是 ,为什么? 2.如图(2),点D在AB上,点E在AC上,CD与BE相交于点O,且AD=AE,AB=AC.若∠B=20°,CD=5cm,则∠C= ,BE= .3.如图(3),若OB=OD,∠A=∠C,若AB=3cm,则CD= . ADBC图(1)BCODEA图(2)ADBCO图(3)∠DBC20°5cm3cm试一试二、熟练转化“间接条件”判全等4.如图(4)AE=CF,∠AFD=∠CEB,DF=BE,△AFD与△ CEB全等吗?为什么?5.如图(5)∠CAE=∠BAD,∠B=∠D,AC=AE,△ABC与△ADE全等吗?为什么?6.“三月三,放风筝”如图(6)是小东同学自己做的风筝,他根据AB=AD,BC=DC,不用度量,就知道∠ABC=∠ADC。请用所学的知识给予说明。ADBCFEACEBD解答想一想三、体验感受条件开放题7.填空:如图(7)请你选择适合的条件填入空格中,使两个三角形全等。
①因为DF=DF, , ,根据 , 可知△DEF≌△DGF。
②因为DF=DF, , ,根据 , 可知△DEF≌△DGF。
③因为DF=DF, , ,根 据 , 可知△DEF≌△DGF。
④因为DF=DF, , ,根据 , 可知△DEF≌△DGF。EGDFDE=DG∠EDF=∠GDFSAS∠EDF=∠GDF∠EFD=∠GFDASA∠EDF=∠GDF∠E=∠GAASDE=DGEF=GFSSS议一议四、体验感受结论开放题8.如图(8)△ABE≌△ACD,由此你能得到什么结论?(越多越好)ABCDE睿智点心五、探究合作,数学好玩例⒌如图,等腰直角△ABC的直角顶点C在直线m上,AD⊥m,BE⊥m,垂足分别为D、E.
●试探索AD、BE、DE的大小关系
数学好玩OK“学好几何,必须过三关:语言关、符号关、作图关”可见,准确作图是学好几何的基础,而准确画出一个角的角平分线是我们接触到的几何基本作图之一。从教材上,同学们知道了“工人师傅利用角尺”和“尺规”作一个角的平分线。作为我们同学,没有“角尺”,可能还有部分同学没有圆规。此时,较准确地画出一个角的平分线可能就有困难了。难道我们不用量角器、“角尺”和圆规就没有办法作一个角的平分线了吗?聪明的你,拿出刻度尺或三角板画下图∠AOB的角平分线,试一试,看谁先完成!OAB 举例说明全等三角形与生活的密切联系,与同学交流数学与生活学习反思●我会了…
●我对了…
●还有… …谢谢合作4.如图(4)AE=CF,∠AFD=∠CEB,DF=BE,△AFD与△ CEB全等吗?为什么?解:∵AE=CFADBCFE∴AE-FE=CF-EF即AF=CE又∵ ∠AFD=∠CEB,
DF=BE
根据“SAS”,可以得到△AFD≌△CEB返
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
