第十一章 图形的全等 全等三角形 复习课课件[下学期]
文档属性
| 名称 | 第十一章 图形的全等 全等三角形 复习课课件[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 800.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-04-29 00:00:00 | ||
图片预览




文档简介
课件14张PPT。许河中学 周美华全等三角形复习学习目标:1.回顾本章所学知识内容,构建知识结构框架,使所学知识系统化。
2.熟悉掌握三角形全等的条件,学会多角度.多方位的观察图形和思考问题。
3.进一步学习有条理的思考.清晰地表达自己的意见,能用“因为------根据------所以------”的形式来说理。
4.感受全等三角形与生活的密切联系,体会数学的价值,增强用数学的意识。一.知识点?1. 定义:能够互相重合的两个三角形叫做全等三角形。
?2. 基本性质:全等三角形的对应边相等,对应角相等。3.判定定理:SAS ASA AAS SSS HL动手操作
领悟知识
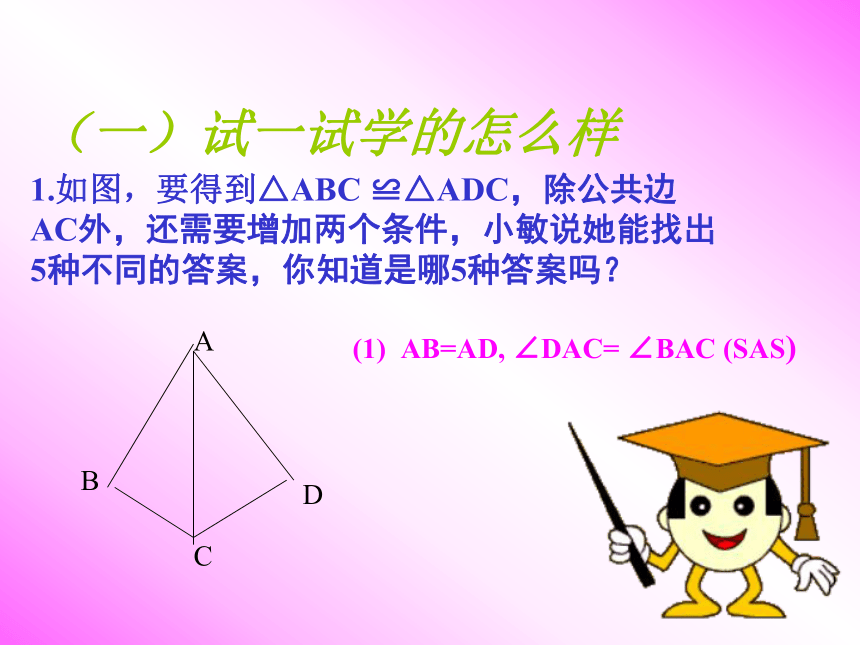
感受生活(一)试一试学的怎么样1.如图,要得到△ABC ≌△ADC,除公共边AC外,还需要增加两个条件,小敏说她能找出5种不同的答案,你知道是哪5种答案吗?
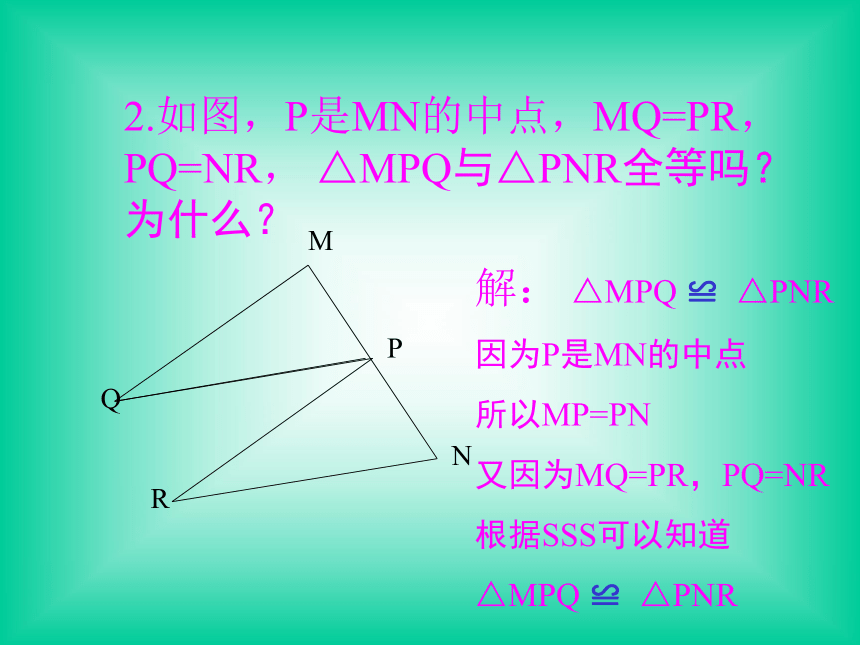
ABCD(1) AB=AD, ∠DAC= ∠BAC (SAS)2.如图,P是MN的中点,MQ=PR,PQ=NR, △MPQ与△PNR全等吗?为什么?MQPRN解: △MPQ ≌ △PNR
因为P是MN的中点
所以MP=PN
又因为MQ=PR,PQ=NR
根据SSS可以知道
△MPQ ≌ △PNR
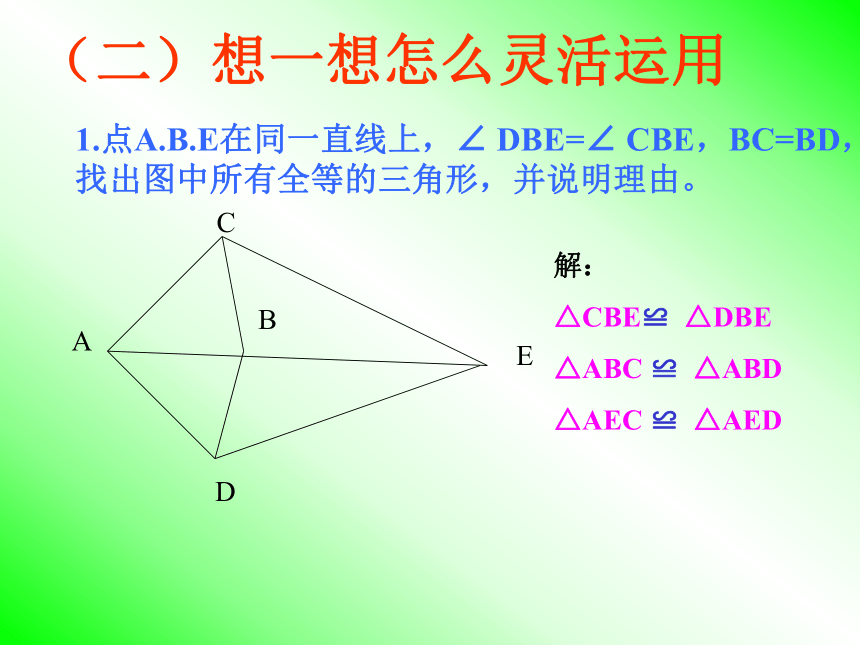
1.点A.B.E在同一直线上,∠ DBE=∠ CBE,BC=BD,找出图中所有全等的三角形,并说明理由。CADEB解:
△CBE≌ △DBE
△ABC ≌ △ABD
△AEC ≌ △AED
(二)想一想怎么灵活运用
(三).让 我 们 一 起 来 探 索 研 究
如图. ∠ ACB=90°,AC=BC,BE ⊥ CE,AD⊥ CE,垂足分别为E,D,图中 有那条线段与AD相等,并说明理由。BEACD解:AD=CE
因为BE ⊥CE,AD ⊥CE,
所以∠ BEC= ∠ CDA= 90°
又因为∠ ACB=90°,
即∠ BCE+ ∠ ACE=90°
∠ DAC+ ∠ ACD=90°
所以∠ BCE= ∠ DAC,
又因为AC=BC
根据AAS,可以知道△BEC≌△CDA
所以AD=CE 课堂练习
1.如图1,AB=CD,AC=BD,则与∠ACB相等的角是________,为什么?
2.如图2,点D在AB上,点E在AC上,CD与BE相交于点O,且AD=AE,AB=AC。若∠B=200,CD=5cm,则∠C=______,BE=_______.
3.如图.AB=EB,BC=BF,∠ ABE=∠ CBF,EF和 AC相等吗?为什么?CEFBA通过这节课的学习你有什么收获?我会了-------
我懂了-------
还有------生活真美,生活中有数学,我们爱生活,我们爱数学,因为它可以使我们睿智。 课堂作业 遨游了知识的海洋,老师发现你们是很棒的,做作业可要小心细致呦!P167. 6. 7. 8.同学们再见!
祝 你 们 学 习 进 步 !
2.熟悉掌握三角形全等的条件,学会多角度.多方位的观察图形和思考问题。
3.进一步学习有条理的思考.清晰地表达自己的意见,能用“因为------根据------所以------”的形式来说理。
4.感受全等三角形与生活的密切联系,体会数学的价值,增强用数学的意识。一.知识点?1. 定义:能够互相重合的两个三角形叫做全等三角形。
?2. 基本性质:全等三角形的对应边相等,对应角相等。3.判定定理:SAS ASA AAS SSS HL动手操作
领悟知识
感受生活(一)试一试学的怎么样1.如图,要得到△ABC ≌△ADC,除公共边AC外,还需要增加两个条件,小敏说她能找出5种不同的答案,你知道是哪5种答案吗?
ABCD(1) AB=AD, ∠DAC= ∠BAC (SAS)2.如图,P是MN的中点,MQ=PR,PQ=NR, △MPQ与△PNR全等吗?为什么?MQPRN解: △MPQ ≌ △PNR
因为P是MN的中点
所以MP=PN
又因为MQ=PR,PQ=NR
根据SSS可以知道
△MPQ ≌ △PNR
1.点A.B.E在同一直线上,∠ DBE=∠ CBE,BC=BD,找出图中所有全等的三角形,并说明理由。CADEB解:
△CBE≌ △DBE
△ABC ≌ △ABD
△AEC ≌ △AED
(二)想一想怎么灵活运用
(三).让 我 们 一 起 来 探 索 研 究
如图. ∠ ACB=90°,AC=BC,BE ⊥ CE,AD⊥ CE,垂足分别为E,D,图中 有那条线段与AD相等,并说明理由。BEACD解:AD=CE
因为BE ⊥CE,AD ⊥CE,
所以∠ BEC= ∠ CDA= 90°
又因为∠ ACB=90°,
即∠ BCE+ ∠ ACE=90°
∠ DAC+ ∠ ACD=90°
所以∠ BCE= ∠ DAC,
又因为AC=BC
根据AAS,可以知道△BEC≌△CDA
所以AD=CE 课堂练习
1.如图1,AB=CD,AC=BD,则与∠ACB相等的角是________,为什么?
2.如图2,点D在AB上,点E在AC上,CD与BE相交于点O,且AD=AE,AB=AC。若∠B=200,CD=5cm,则∠C=______,BE=_______.
3.如图.AB=EB,BC=BF,∠ ABE=∠ CBF,EF和 AC相等吗?为什么?CEFBA通过这节课的学习你有什么收获?我会了-------
我懂了-------
还有------生活真美,生活中有数学,我们爱生活,我们爱数学,因为它可以使我们睿智。 课堂作业 遨游了知识的海洋,老师发现你们是很棒的,做作业可要小心细致呦!P167. 6. 7. 8.同学们再见!
祝 你 们 学 习 进 步 !
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
