高一数学2.1.1 根式与分数指数幂.ppt
文档属性
| 名称 | 高一数学2.1.1 根式与分数指数幂.ppt |  | |
| 格式 | zip | ||
| 文件大小 | 532.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-08-26 16:56:02 | ||
图片预览



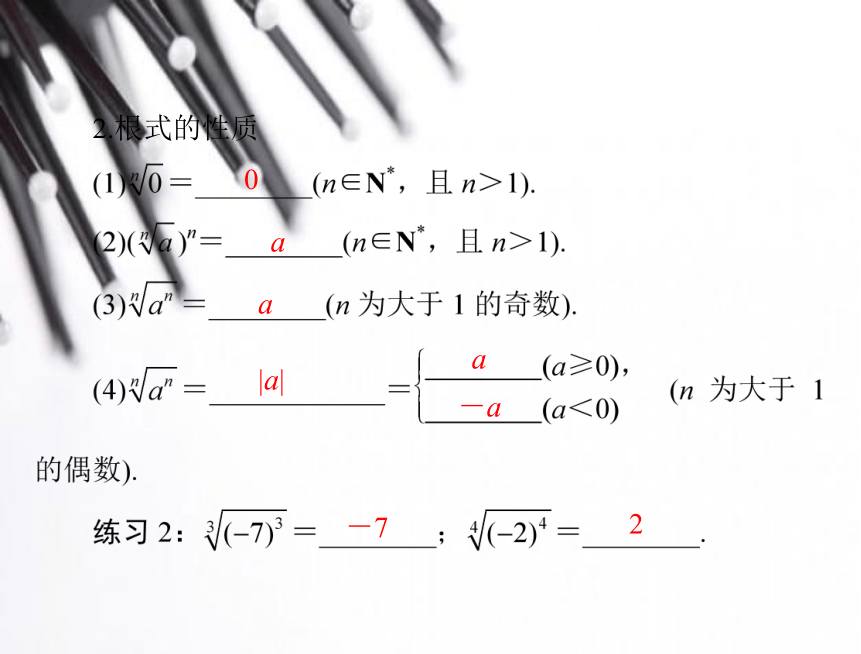



文档简介
课件18张PPT。第二章基本初等函数(Ⅰ) 2.1 指数函数
2.1.1 根式与分数指数幂【学习目标】1.理解 n 次方根及根式的概念.
2.理解根式的运算性质.
3.理解分数指数幂的意义.4.掌握根式与分数指数幂的互化.1.根式的概念xn=a (1)a 的 n 次方根:如果________,那么 x 叫做 a 的 n 次方
根,其中 n>1,且 n∈N*.当 n 是奇数时,a 的 n 次方根表示为
________,a∈________;当 n 是偶数时,a 的 n 次方根表示为________,a∈___________.R(0,+∞)做____________.根式被开方数2±2练习 1:8 的 3 次方根是______,16 的 4 次方根是______.根指数0aa|a|a-a2.根式的性质-723.分数指数幂的意义0没有意义270【问题探究】1.(±2)2=4,那么±2 就叫做 4 的____________;
33=27,那么 3 就叫做 27 的____________;
(±3)4=81,那么±3 就叫做 81 的____________.依此类推,若 xn=a,那么 x 叫做 a 的______________.
答案:二次方根 立方根 四次方根 n 次方根题型 1 根式的求值、化简
【例 1】 求下列各式的值:思维突破:运用根式的性质及运算公式计算.【变式与拓展】1.求下列各式的值:2.化简:题型 2 根式的比较大小思维突破:先化为统一的根指数,再进行比较.当根指数相同时,不论根指数是奇数还是偶数,根式的大小取决于被开方数的大小.【变式与拓展】题型 3 分数指数幂与根式的互化
【例 3】 将下列分数指数幂化为根式(其中 a>0):思维突破:根据分数指数幂的意义计算.【变式与拓展】
4.将下列分数指数幂化为根式: [方法·规律·小结]2.分数指数幂.(2)根式与分数指数幂表示相同意义的量,只是形式不同.(3)有理数包括整数和分数,由整数指数幂扩充到分数指数幂后,指数概念就扩充到了有理数指数幂.
2.1.1 根式与分数指数幂【学习目标】1.理解 n 次方根及根式的概念.
2.理解根式的运算性质.
3.理解分数指数幂的意义.4.掌握根式与分数指数幂的互化.1.根式的概念xn=a (1)a 的 n 次方根:如果________,那么 x 叫做 a 的 n 次方
根,其中 n>1,且 n∈N*.当 n 是奇数时,a 的 n 次方根表示为
________,a∈________;当 n 是偶数时,a 的 n 次方根表示为________,a∈___________.R(0,+∞)做____________.根式被开方数2±2练习 1:8 的 3 次方根是______,16 的 4 次方根是______.根指数0aa|a|a-a2.根式的性质-723.分数指数幂的意义0没有意义270【问题探究】1.(±2)2=4,那么±2 就叫做 4 的____________;
33=27,那么 3 就叫做 27 的____________;
(±3)4=81,那么±3 就叫做 81 的____________.依此类推,若 xn=a,那么 x 叫做 a 的______________.
答案:二次方根 立方根 四次方根 n 次方根题型 1 根式的求值、化简
【例 1】 求下列各式的值:思维突破:运用根式的性质及运算公式计算.【变式与拓展】1.求下列各式的值:2.化简:题型 2 根式的比较大小思维突破:先化为统一的根指数,再进行比较.当根指数相同时,不论根指数是奇数还是偶数,根式的大小取决于被开方数的大小.【变式与拓展】题型 3 分数指数幂与根式的互化
【例 3】 将下列分数指数幂化为根式(其中 a>0):思维突破:根据分数指数幂的意义计算.【变式与拓展】
4.将下列分数指数幂化为根式: [方法·规律·小结]2.分数指数幂.(2)根式与分数指数幂表示相同意义的量,只是形式不同.(3)有理数包括整数和分数,由整数指数幂扩充到分数指数幂后,指数概念就扩充到了有理数指数幂.
