高一数学2.1.2 指数幂的运算.ppt
文档属性
| 名称 | 高一数学2.1.2 指数幂的运算.ppt |

|
|
| 格式 | zip | ||
| 文件大小 | 415.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-08-26 16:56:23 | ||
图片预览







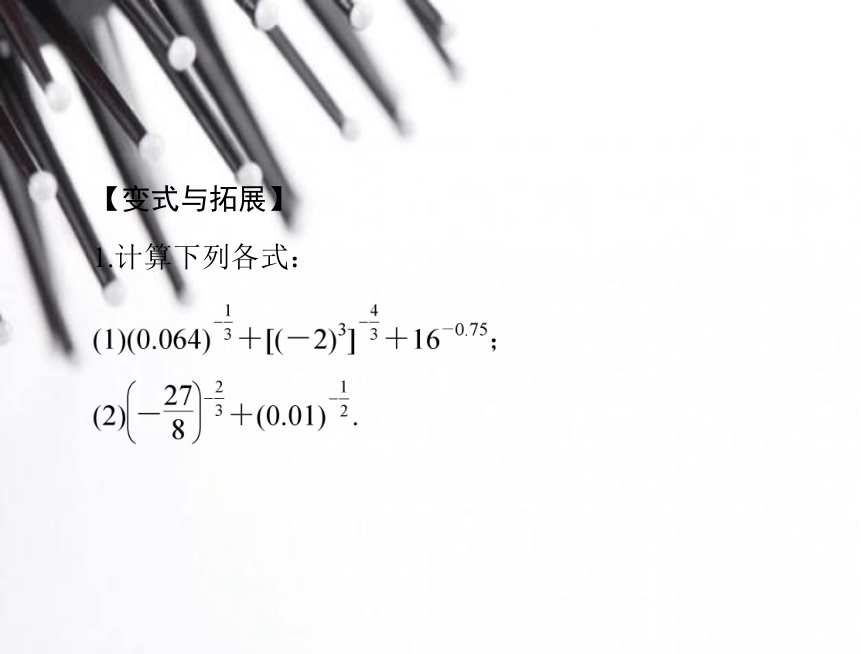
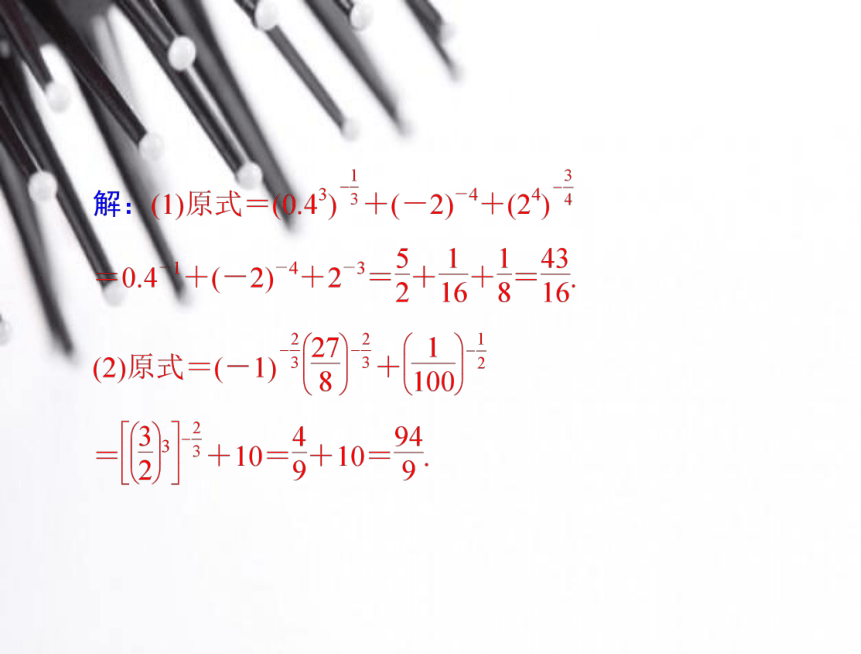
文档简介
课件21张PPT。.2.1.2 指数幂的运算【学习目标】1.掌握分数指数幂的运算.3.掌握有理数指数幂的运算性质.1.有理数指数幂的运算性质12(1)aras=________(a>0,r,s∈Q).
(2)(ar)s=________(a>0,r,s∈Q).
(3)(ab)r=________(a>0,b>0,r∈Q).
练习1:22·2-3=________;
(32)3=________;ar+sarsarbr36 2.无理数指数幂
无理数指数幂 aα(a>0,α是无理数)是一个确定的实数.
有理数指数幂的运算性质对无理数指数幂同样适用.
127【问题探究】1.0 的正分数指数幂为______,0 的负分数指数幂______.
答案:0 无意义2.分数指数幂有什么运算性质?答案:分数指数幂的运算性质有:
(1)ar·as=ar+s(a>0,r,s∈Q).
(2)(ar)s=ars(a>0,r,s∈Q).
(3)(ab)r=arbr(a>0,b>0,r∈Q).题型 1 分数指数幂的运算
【例 1】 求下列各式的值:思维突破:利用分数指数幂的运算性质求值.【变式与拓展】
1.计算下列各式:题型 2 分数指数幂与根式的混合运算
【例 2】 求下列各式的值: 式子中既含有分数指数幂,又含有根式,应该
把根式统一化成分数指数幂的形式,以便于运算.【变式与拓展】题型 3 带有附加条件的求值问题
【例 3】 求值:
(1)已知2x+2-x=a(a为常数),求8x+8-x的值;注:a3+b3=(a+b)(a2-ab+b2)
a3-b3=(a-b)(a2+ab+b2)思维突破:从整体中寻求结果与条件的联系,整体代入求值.解:(1)令2x=t,则2-x=t-1.
∴t+t-1=a. ①
方法一:由①两边平方,得t2+t-2=a2-2.
∴8x+8-x=t3+t-3
=(t+t-1)(t2-t·t-1+t-2)
=a(a2-2-1)
=a3-3a.方法二:8x+8-x=t3+t-3
=(t+t-1)(t2-t·t-1+t-2)
=a[(t+t-1)2-3t·t-1]
=a(a2-3)
=a3-3a. 对于“条件求值”问题一定要弄清已知与未
知的联系,然后采取“整体代换”或“求值后代换”两种方法
求值.【变式与拓展】 3.已知x+x-1=5,求代数式x2+x-2的值.
解:由x+x-1=5两边平方,得x2+2+x-2=25,则x2+
x-2=23.【例4】 已知x+x-1=3,求x2-x-2的值.[方法·规律·小结]
1.有理数指数幂的运算性质.
(1)在有理数指数幂的运算性质中,等式均在有意义的条件
(2)在(ar)s=ars(a>0,r,s∈Q)中,r,s还可以进一步推广
到无理数、实数.2.无理数指数幂的意义.有理数指数幂可以扩展到无理数指数幂,我们采用“有理数逼近无理数”的思想认识无理数指数幂的大小.对于任意的0,0 的负无理数次幂没有意义. 3.分数指数幂的定义揭示了分数指数幂与根式的关系,因
此,根式的运算可以先转化成分数指数幂的形式,再进行运算,则,并且要注意运算的顺序.
(2)(ar)s=________(a>0,r,s∈Q).
(3)(ab)r=________(a>0,b>0,r∈Q).
练习1:22·2-3=________;
(32)3=________;ar+sarsarbr36 2.无理数指数幂
无理数指数幂 aα(a>0,α是无理数)是一个确定的实数.
有理数指数幂的运算性质对无理数指数幂同样适用.
127【问题探究】1.0 的正分数指数幂为______,0 的负分数指数幂______.
答案:0 无意义2.分数指数幂有什么运算性质?答案:分数指数幂的运算性质有:
(1)ar·as=ar+s(a>0,r,s∈Q).
(2)(ar)s=ars(a>0,r,s∈Q).
(3)(ab)r=arbr(a>0,b>0,r∈Q).题型 1 分数指数幂的运算
【例 1】 求下列各式的值:思维突破:利用分数指数幂的运算性质求值.【变式与拓展】
1.计算下列各式:题型 2 分数指数幂与根式的混合运算
【例 2】 求下列各式的值: 式子中既含有分数指数幂,又含有根式,应该
把根式统一化成分数指数幂的形式,以便于运算.【变式与拓展】题型 3 带有附加条件的求值问题
【例 3】 求值:
(1)已知2x+2-x=a(a为常数),求8x+8-x的值;注:a3+b3=(a+b)(a2-ab+b2)
a3-b3=(a-b)(a2+ab+b2)思维突破:从整体中寻求结果与条件的联系,整体代入求值.解:(1)令2x=t,则2-x=t-1.
∴t+t-1=a. ①
方法一:由①两边平方,得t2+t-2=a2-2.
∴8x+8-x=t3+t-3
=(t+t-1)(t2-t·t-1+t-2)
=a(a2-2-1)
=a3-3a.方法二:8x+8-x=t3+t-3
=(t+t-1)(t2-t·t-1+t-2)
=a[(t+t-1)2-3t·t-1]
=a(a2-3)
=a3-3a. 对于“条件求值”问题一定要弄清已知与未
知的联系,然后采取“整体代换”或“求值后代换”两种方法
求值.【变式与拓展】 3.已知x+x-1=5,求代数式x2+x-2的值.
解:由x+x-1=5两边平方,得x2+2+x-2=25,则x2+
x-2=23.【例4】 已知x+x-1=3,求x2-x-2的值.[方法·规律·小结]
1.有理数指数幂的运算性质.
(1)在有理数指数幂的运算性质中,等式均在有意义的条件
(2)在(ar)s=ars(a>0,r,s∈Q)中,r,s还可以进一步推广
到无理数、实数.2.无理数指数幂的意义.有理数指数幂可以扩展到无理数指数幂,我们采用“有理数逼近无理数”的思想认识无理数指数幂的大小.对于任意的0,0 的负无理数次幂没有意义. 3.分数指数幂的定义揭示了分数指数幂与根式的关系,因
此,根式的运算可以先转化成分数指数幂的形式,再进行运算,则,并且要注意运算的顺序.
